大跨度铁路桥梁整体变形波长特征分析
赵健业 胡所亭 郭辉 张楠 苏朋飞 廖晓璇
1.中国铁道科学研究院, 北京 100081; 2.中国铁道科学研究院集团有限公司 铁道建筑研究所, 北京 100081;3.中国铁道科学研究院集团有限公司 高速铁路轨道系统全国重点实验室, 北京 100081;4.北京交通大学 土木建筑工程学院, 北京 100044
随着高速铁路快速发展,列车运营速度不断提高,大跨度铁路桥梁的高平顺性成为核心问题。目前,国内外对线路的中短波轨道不平顺的标准进行了大量研究[1-4],但对大跨度铁路桥上不同波长的轨道不平顺管理的研究有所欠缺。
高速铁路运营实践经验表明,长波不平顺主要影响旅客乘坐舒适性[5],中短波不平顺主要影响列车运行安全性、平稳性并产生高频振动和噪声[6]。而大跨度铁路桥梁变形引起的轨道附加不平顺多呈现为长波不平顺。
鉴于此,本文分析A、B、C三座大跨度铁路桥梁在温度、沉降、风、列车等作用下的桥面变形波长特征,研究结果对于大跨度铁路桥上轨道不平顺评价控制及后期运维具有指导作用。
1 整体计算模型说明
A桥为五跨连续结构,主桥跨径布置为(84 + 84 +1 092 + 84 + 84) m,承载四线高速铁路、八车道高速公路。铁路设计速度250 km/h。两主塔采用门式框架结构,桥塔基础采用大直径群桩基础。采用MIDAS Civil软件建立有限元模型[图1(a)]。模型划分11 141个节点,28 012个单元。主梁、索塔和桥墩采用梁单元模拟,吊索采用只受拉杆单元模拟,主缆采用索单元模拟。
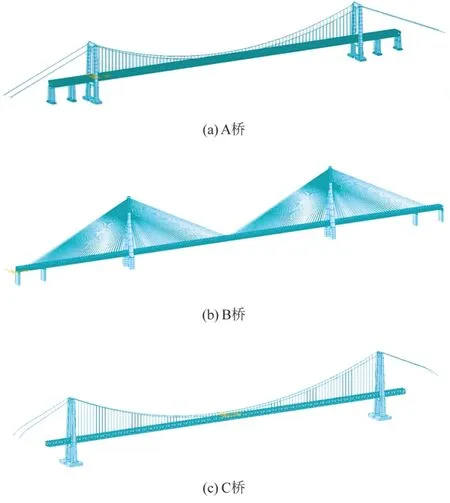
图1 有限元模型
B桥为两塔五跨钢桁梁斜拉桥[图1(b)],采用三索面三主桁结构,主桥跨径布置为(140 + 462 + 1 092 +462 + 140) m,承载四线铁路、六车道高速公路。其中下游侧两线铁路设计速度200 km/h,上游侧两线铁路设计速度250 km/h。模型共划分9 555个节点,14 580个单元。主梁、索塔和桥墩采用梁单元模拟,斜拉索采用索单元模拟。
C桥主缆跨度为(250 + 1 140 + 250) m,桥梁跨度为(80 + 1 140 + 80) m,桥上设置双线铁路。模型[图1(c)]共划分2 164个节点,4 274个单元。主梁、索塔和桥墩采用梁单元模拟,吊索采用只受拉杆单元模拟,主缆采用索单元模拟。
2 轨面变形计算
计算三座大桥在整体升降温、桥塔沉降、横向静风力、列车整体加载等作用下的桥面整体变形,即长波变形。由于桥轨之间相对位移波长不超过数个扣件节间,只影响轨面短波变形,因而计算时不区分桥面变形与轨面变形的差异,认为桥梁和轨道之间的整体线形变化具有同步性。具体做法如下。
A桥:研究竖向变形时,四线铁路对称,内侧线路和外侧线路分别考虑;研究横向变形时,四线铁路分别考虑;对竖向和横向变形,每线线路均取2根铁路纵梁变形的平均值。
B桥:桥面为密布横梁体系,布设小纵梁。研究竖向变形时,计算密布横梁各点的平均值;研究横向变形时,上游侧线路和下游侧线路分别考虑。
C桥:桥上线路为双线,研究竖向变形时,取4根铁路纵梁变形的平均值;研究横向变形时,上游侧线路和下游侧线路分别考虑;对竖向和横向变形,每线线路均取2根铁路纵梁变形的平均值。
2.1 整体温度作用下的轨面变形
由于三座桥梁计算模型均为线性系统,因此升、降相同温度所引起的轨道梁变形大小相等,方向相反。分析中仅研究升温情况。升温工况按照设计资料选定:A桥、B桥整体升温35.0 ℃,C桥整体升温33.8 ℃。对于四线桥,仅展示最不利的外侧线路。通过静力计算可得三座桥梁在整体升温作用下轨面垂向变形曲线见图2。
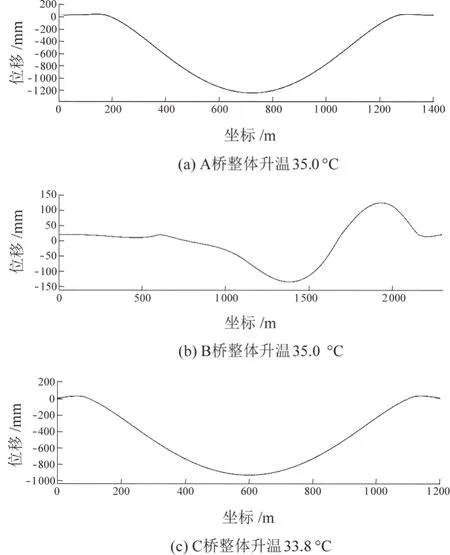
图2 桥梁整体升温作用下轨面垂向变形曲线
2.2 桥塔沉降作用下的轨面变形
桥塔沉降幅度按照设计资料选定,A桥、B桥在小里程侧桥塔沉降10 cm条件下,C桥在小里程侧桥塔沉降5 cm条件下轨面垂向变形见图3。由于桥梁结构对称,本文仅考虑一侧桥塔沉降的工况。对于四线桥,仅展示最不利的外侧线路。
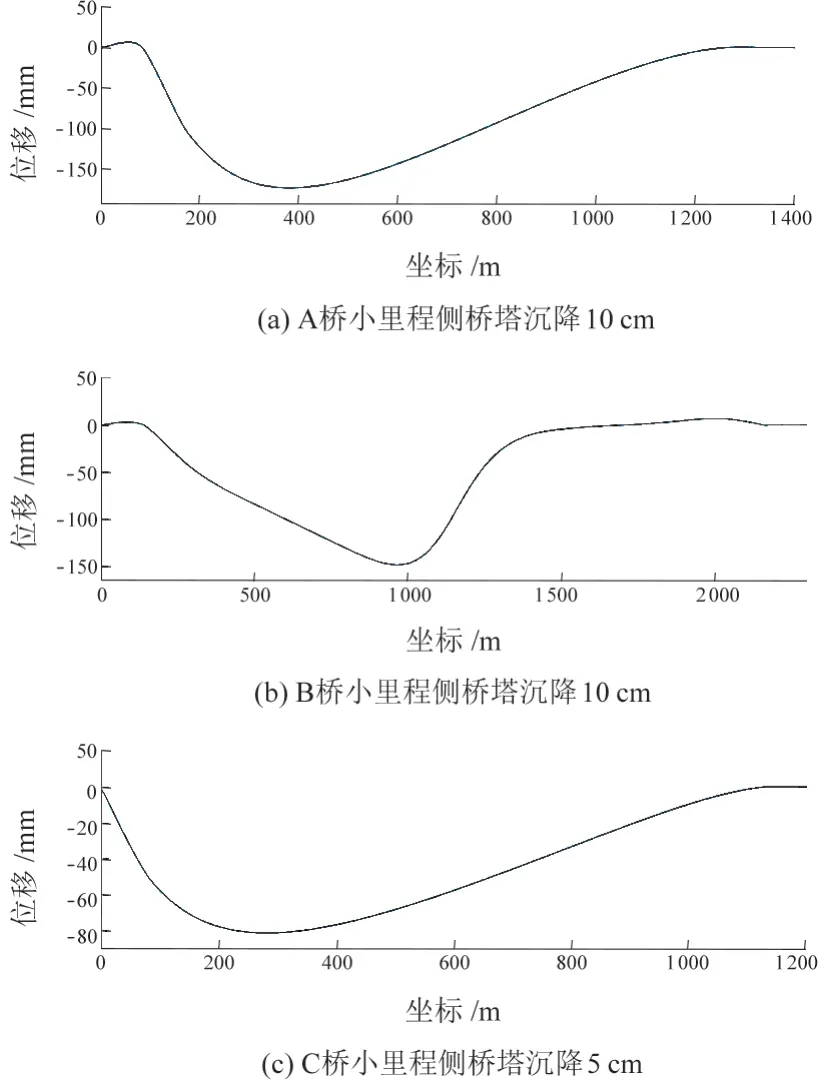
图3 桥梁小里程侧桥塔沉降作用下轨道梁垂向变形曲线
2.3 静风力作用下的轨面变形
依据设计资料,分别对A桥、B桥、C桥施加9.04、14.36、3.14 kN/m的横向风荷载,三座桥梁在静风荷载作用下的轨面横向变形曲线见图4。对于四线桥,仅展示最不利的背风侧外侧线路。
2.4 列车作用下的全局轨面变形
列车全局荷载作用下,考虑16节编组对桥梁整体变形的影响规律。计算中采用列车每1 m前行一步的方式,计算了桥跨中各处的轨面垂向变形,见图5。其中黑线代表最大变形,红线代表最小变形。
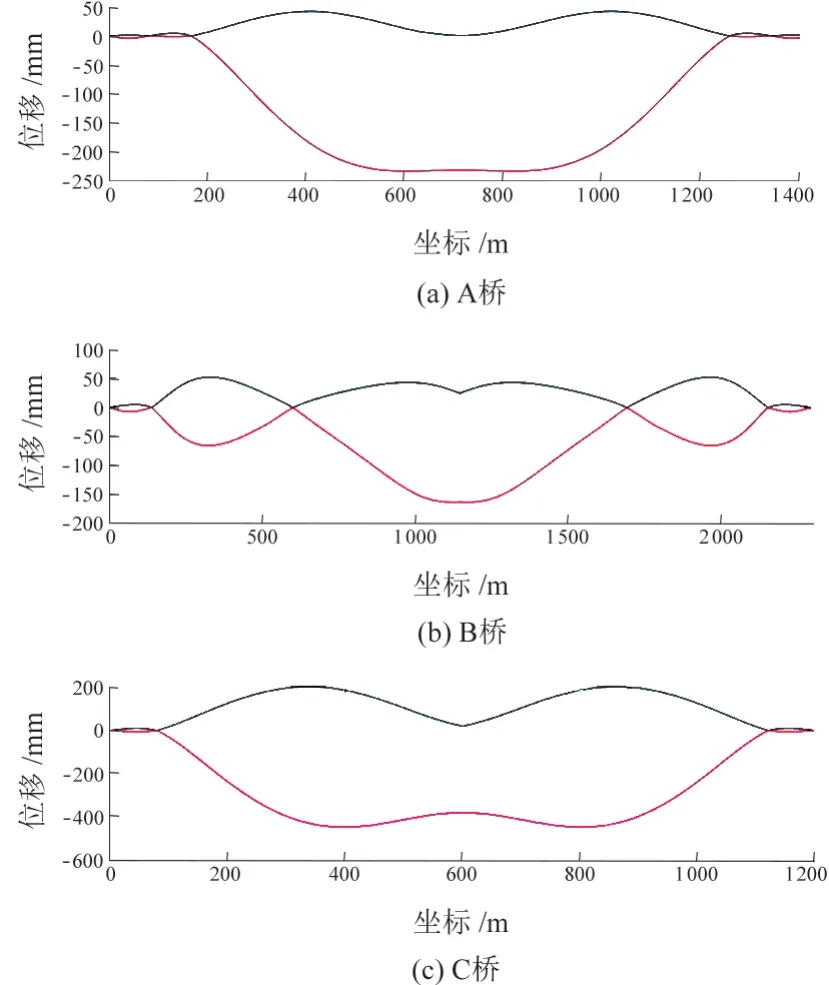
图5 列车全局荷载作用下垂向变形曲线
2.5 轨面变形小结
各工况下轨面变形最大值及位置见表1。可见,在整体升降温、静风荷载及全局列车荷载作用下,三座桥梁轨面变形最大值均在中跨跨中附近,而桥塔沉降作用下轨面变形最大值则位于中跨靠近沉降桥塔一侧。
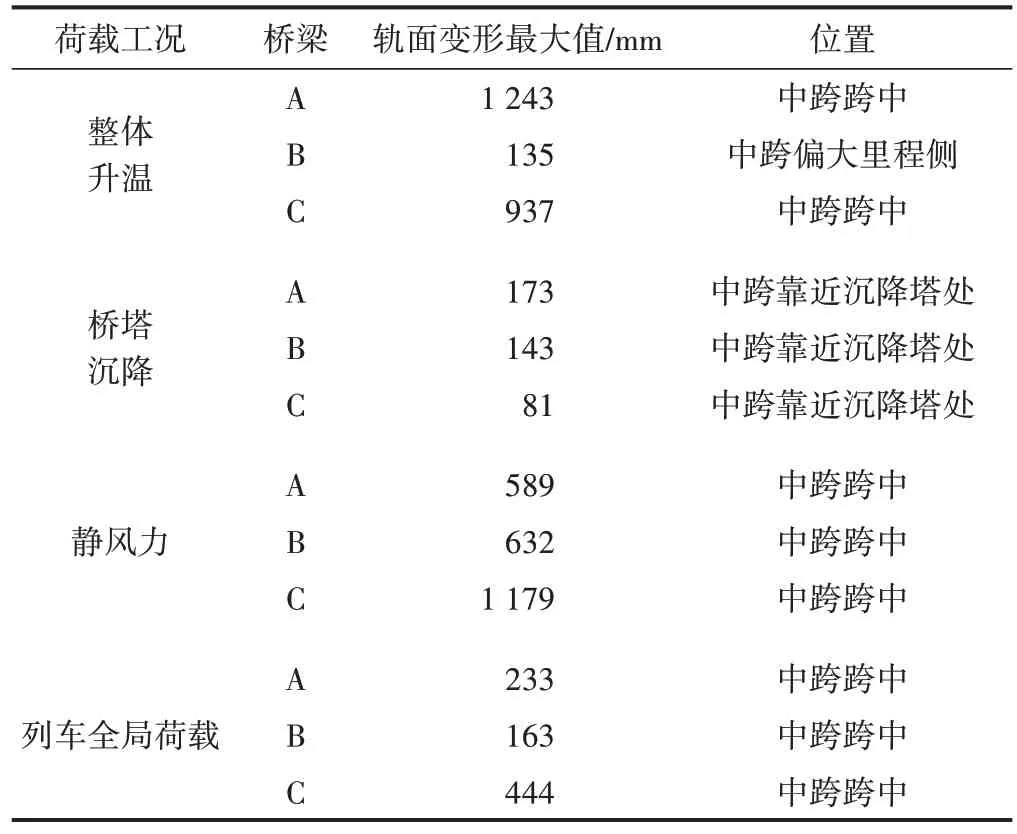
表1 各工况轨面变形最大值及位置
一般认为,加劲梁的变形是否平顺决定了轨面曲率半径,而曲率半径较小处对行车不利。在整体温度、桥塔沉降、静风荷载及列车全局荷载作用下,三座桥梁轨面变形的曲率半径最小位置主要集中在梁端、边跨及塔梁相接处,这些位置亦是开展车桥耦合动力分析的关键部位。
3 轨面变形波长分析方法及选取原则
3.1 波长分析方法
理论上,采用傅里叶变换或类似方法可计算得到给定变形的波长成分,但大跨度桥梁在全局荷载作用下变形的周期性不显著,直接采用此类分析方法精度低且存在不可忽略的计算误差。
为定量分析整体温度作用、桥塔沉降、静风力、列车全局作用四种长波变形的波长成分及变形特征,经理论分析与比选,本文采用HHT方法分析桥梁整体变形曲线的波长[7]。其过程是:先对信号进行经验模态分解,得出本征模态函数;再对本征模态函数进行希尔伯特变换,从而进一步得到该信号的希尔伯特谱,以便对信号进行分析。
此外,分析中还用到中点弦测法[8]和曲率半径法定量表述桥面变形曲线的性质,分述如下。
1)中点弦测法
中点弦测法即利用车体与3个轮对在车辆上建立测量基准线进行轨道高低和轨向测量。将检测车前后两轮与轨道接触点的连线作为测量基准线,中间轮与轨道接触点偏离基准线的大小作为不平顺的测量结果,即矢度值。图6说明了中点弦测法测量原理。
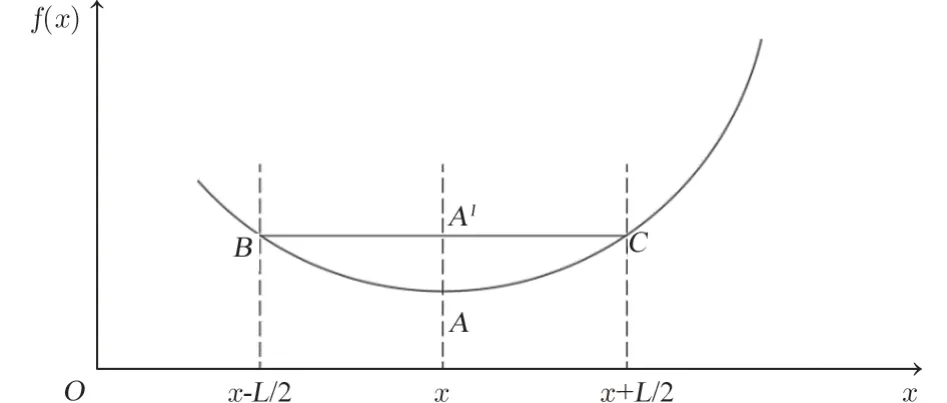
图6 中点弦测法原理示意
将图6中A位置对应弦长L的弦测值M(x)定义为线段AA'的长度,可用下式计算:
式中,xA为中点弦测法所定义的位置。
实际工程中,以测点前后一定距离的轮轨接触点连线BC作为基准线,而BC未必与x轴平行,但可以证明,线段BC的斜率为弦测值M(x)的高阶无穷小,因此后续分析中将BC视为平行于x轴的线段。参考类似工程经验,本文采用弦长30、60 m两种中心弦测值对轨面变形进行分析和评判。
长波成分对行车安全性影响较小。参考既有相关规定,计算30 m弦测值时应先将波长超出60 m的成分滤波去除;计算60 m弦测时应先将波长超出200 m的成分滤波去除[9]。
2)曲率半径法
曲率半径法即直接通过曲率定义计算曲线上某点的曲率,并取其倒数为曲率半径。中点弦测法的本质是考察线路的垂向及水平向曲率,但中点弦测法对不同波长成分和波长成分组合的敏感性难以量化表示,由此,本文同时采用曲率半径表征轨面变形的剧烈程度。
设轨面f(x)变形为正弦函数,波幅为A0,波长为L0,则
由此,曲率(K)为
对应正弦曲线顶点,即x= π/2时,有
因此,名义曲率半径R为
由式(5)可知,如将变形曲线视为正弦曲线,则弦测值与曲率半径之间存在固定关系。例如,30 m弦1 mm弦测矢度相当于91 189 m曲率半径,60 m弦1 mm弦测矢度相当于364 756 m曲率半径。后续分析中,本文拟由式(5)先计算名义曲率半径,进而将轨面变形等价于给定弦长的弦测矢度值。
3.2 波段选取原则
研究波幅过小的曲线成分对行车安全性分析是没有意义的。因此本文对于HHT方法计算的波长成分,只考虑波幅超过1 mm的曲线段。
参照某大跨度铁路桥梁的线桥运营维修管理规定,30 m弦测对应的作业验收、舒适度、临时补修、限速四档矢度限值为5、8、10、13 mm,250 km/h速度下60 m弦测对应作业验收标准矢度限值为10 mm。
曲线段在荷载作用下,不显著的波幅对行车安全性影响极小,不具有研究价值;本文仅研究波幅在3 mm以上的曲线段,并设置曲率半径364 756 m为关注上限。由式(4)、式(5)计算可知,该曲率半径限值即相当于60 m弦测1 mm。对于曲率半径很大(曲线平缓)的曲线段,不存在波幅达到3 mm的曲线段,将所研究的波幅限值降低至1 mm。
此外,由于HHT变换在梁端部分存在误差,且计算模型中并未考虑梁端伸缩装置的影响,本文不研究梁端半个节间范围内的波长特征。
4 波长及波幅分析
以HHT方法分析三座桥梁在整体温度作用、桥塔沉降、静风力、列车荷载全局作用下桥面垂向变形的波长及波幅,见图7—图10。各工况下桥面变形的最小曲率半径及对应的波长与波幅见表2。统计分析中,仅考虑波长在1 ~ 200 m的曲线段。
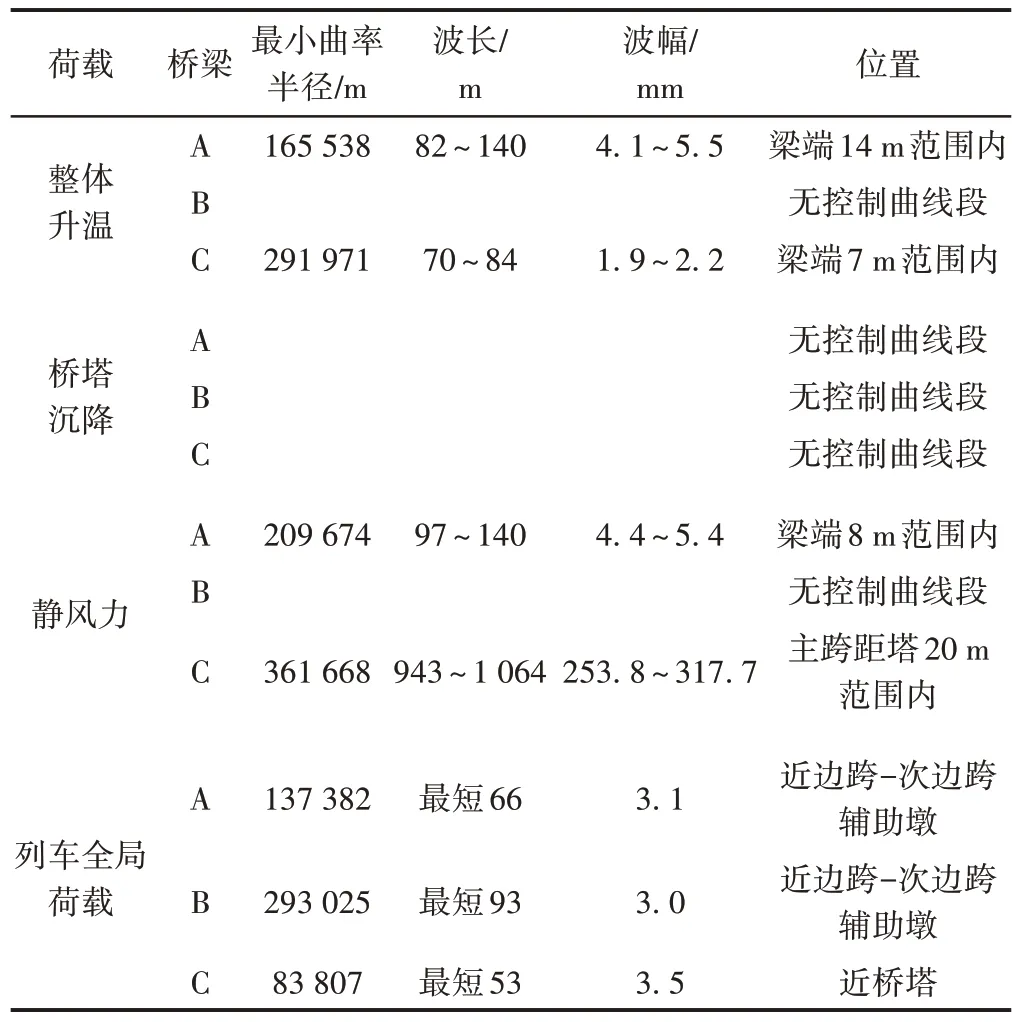
表2 控制曲线段的波长与波幅
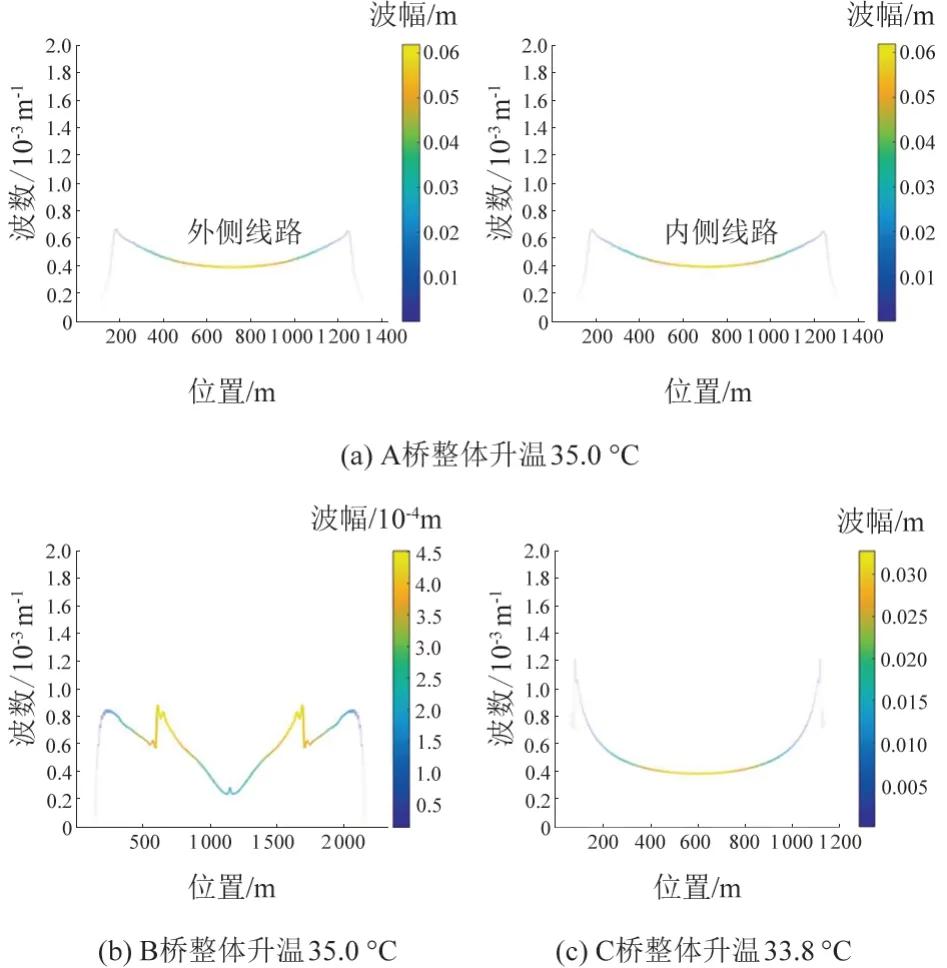
图7 桥梁整体升温作用下桥面波长及波幅
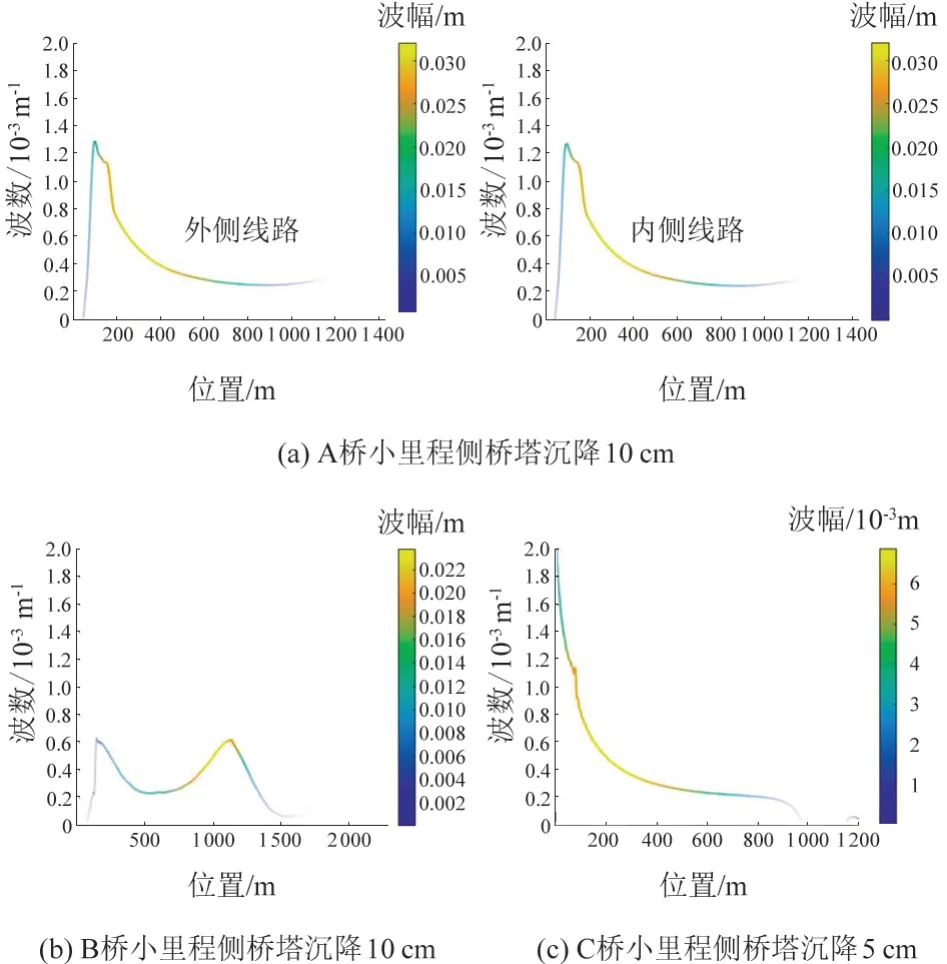
图8 桥梁小里程侧桥塔沉降作用下桥面波长及波幅
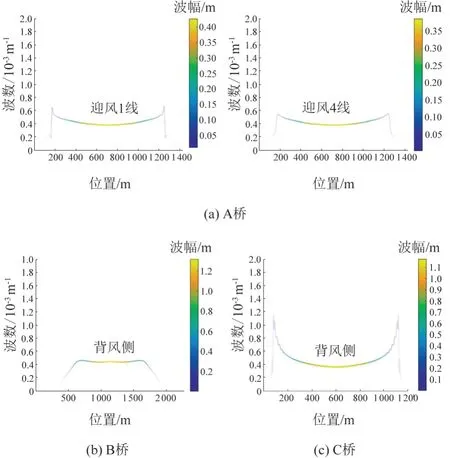
图9 桥梁在静风力作用下桥面波长及波幅
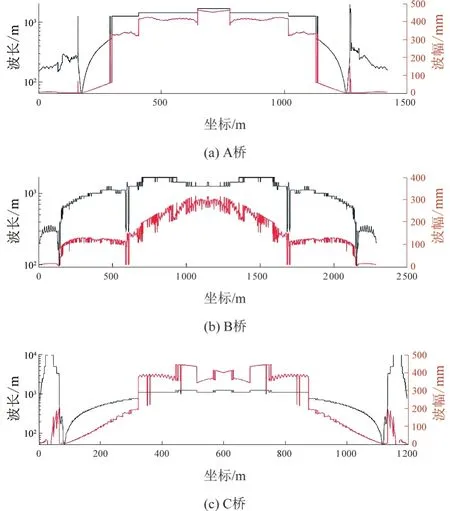
图10 列车全局荷载作用下桥面波长及波幅
长波长、大曲率半径的曲线对行车影响极小,可忽略不计。因此,分析HHT方法计算结果时,采用了前置条件,即,由式(5)计算的名义曲率半径小于364.756 km且波长大于1 mm。例如,A桥升温工况下,满足上述条件的只在距离边支座82 ~ 140 m。虽然此段曲线变形幅值数值远小于桥梁跨中段,但桥梁跨中对应的曲率半径约为2 680 km,已不致对桥梁的行车性能产生显著影响,故不计入统计范围。其余工况的状况与A桥升温工况类似。
由计算结果可见:
1)A桥在整体升温、静风力作用下分别产生82 ~140 m和97 ~ 140 m较长波长的变形,且此类变形的最大幅值仅为5.5 mm;由于其设计荷载较大,桥塔沉降未对其桥面变形产生显著影响。
2)B桥设计荷载大且采用密布横梁体系,加劲肋及桥面刚度亦较大;整体升降温、桥塔沉降、静风荷载均不会对其桥面变形产生显著影响。
3)C桥设计刚度相对较小,在整体升温作用下产生70 ~ 84 m波长的变形,最大幅值为2.2 mm;由于该桥梁主跨两侧仅有一个辅助跨,在静风力作用下产生943 ~ 1 064 m波长的超长波变形,最大幅值为317.7 mm。此波段波长较长,不会对行车安全产生显著影响。桥塔沉降未对其桥面变形产生显著影响。
4)列车全局荷载对三座桥梁的桥面变形产生影响。如关注幅值3 mm及以上的曲线段,A、B、C三座桥最短波长依次为66、93、53 m,对应最小曲率半径依次为137 382、293 025、83 807 m。
5)就研究的三座桥梁而言,荷载引起的桥面垂向变形对行车性能影响的显著程度均依次为列车全局荷载、整体升温、桥塔沉降。由于静风荷载引起桥面横向变形,与前述三者不做比较。
轨面变形影响因素众多,荷载作用下桥面变形复杂,不仅受主梁刚度、桥塔刚度、斜拉索(主缆、吊杆)系统整体刚度的影响,亦十分显著地受到纵向固定支座布置、桥面系刚度的影响。此外,加劲梁的垂向、横向刚度应尽量平顺过渡,刚度突变会引起曲率半径急剧减小,降低桥梁的服役性能。
5 结论
本文针对三座背景桥梁,研究了在整体温度作用、桥塔沉降、静风作用、列车全局荷载作用下轨面变形波长分布规律及其影响因素。主要结论如下:
1)对于长波变形,HHT变换可用于分析桥梁在给定设计荷载作用下的波长成分。
2)A桥在整体温度荷载作用下,产生的变形曲线为波长82 ~ 140 m、波幅不超过5.5 mm的曲线段;在静风力作用下,产生的变形曲线为波长97 ~ 140 m、波幅不超过5.4 mm的曲线段。桥塔沉降作用下A桥不产生显著变形曲线。上述三种荷载作用下B桥均不产生显著变形曲线。C桥在整体温度荷载作用下,产生的变形曲线为波长70 ~ 84 m、波幅不超过2.2 mm的曲线段;桥塔沉降和静风力作用下C桥均不产生显著变形曲线。
3)列车全局荷载对三座桥梁的桥面变形产生影响。如关注幅值3 mm及以上的曲线段,A桥、B桥、C桥三座桥梁最短波长依次为66、93、53 m,对应最小曲率半径依次为137 382、293 025、83 807 m。
4)列车全局荷载作用下,具有多个辅助跨的桥梁控制位置在边跨-次边跨之间的辅助墩附近,具有一个辅助跨的桥梁控制位置在桥塔附近。大跨度桥梁的加劲梁应尽量做到刚度平顺过渡,不应出现刚度突变。
5)就所研究的三座桥梁而言,荷载引起的桥面垂向变形对行车性能影响的显著程度均依次为列车全局荷载、整体升温、桥塔沉降。

