不同约束条件下普速铁路平面线形重构效果对比分析
丁有康 王晓凯 楼梁伟 杨立光 张也
1.北京铁科特种工程技术有限公司, 北京 100081; 2.中国铁道科学研究院集团有限公司 铁道建筑研究所, 北京 100081;3.中国铁道科学研究院集团有限公司 高速铁路轨道系统全国重点实验室, 北京 100081
轨道的高平顺性是保证列车安全平稳运行的前提,然而受列车长期荷载作用、外部环境条件变化等因素的影响,轨道几何状态不可避免地发生劣化,对列车运行安全造成不利影响[1]。大机捣固是轨道养护维修作业的重要手段,可在一定程度上改善轨道平顺性状态,提高线路运营品质[2-5]。近年来,随着轨道精密测量技术的快速发展,基于精测数据及线路绝对设计线形的数字化捣固技术逐步应用于我国普速铁路线路养修作业中[6]。其中,线路平纵断面设计线形作为精捣作业的维修基准,其正确性和合理性对捣固作业效果及后期线路运营安全都起着至关重要的作用。然而,由于我国普速铁路长期采用以相对平顺性为主的维护手段,线路平纵断面缺乏绝对控制,当前线形线位与设计台账相比已普遍发生较大变化。因此,须基于轨道控制网采用轨道精密测量仪器快速采集轨道三维坐标,并对线路平纵断面进行重构设计,获取贴合现状的设计线形,并在此基础上完成数字化捣固方案设计[7]。目前普速铁路平纵断面重构设计过程中普遍以整体调整量最小为目标函数,但在线形参数方面,由于技术人员对现有规范要求缺乏合理认识,导致线形参数约束条件选用不一,时常出现线形参数与捣固作业不匹配的现象。如部分技术人员在线形重构设计过程中未对平纵断面线形参数进行合理限制,导致得到的设计结果不符合规范要求;部分技术人员以原始台账为线形参数约束条件,导致重构设计后出现调整量过大、局部需落道等问题。
鉴于此,本文以普速铁路平面线形重构设计为例,结合相关规范要求系统梳理平面线形参数限制因素。在此基础上,以整体平面调整量平方和最小为平面线形重构设计目标函数,提出无约束、原始台账约束和多参数约束条件下平面线形重构原则,并结合现场实测数据对比分析三种约束条件下平面调整量大小、曲线参数和行车安全性的差异。
1 平面线形参数限制因素
线路平面是线路中心线在水平面的投影,由直线、圆曲线和缓和曲线组成,在曲线区段为平衡列车离心力作用通常设置一定的超高[8]。目前我国铁路工务部门在数字化捣固方案设计中普遍要求维持原有超高不变。基于这一要求,平面线形参数限制因素主要包括曲线半径、缓和曲线长度、圆曲线或夹直线最小长度以及特殊地段调整量。
1)曲线半径
曲线半径的调整会引起未被平衡的欠超高和过超高发生变化。为保证列车运行安全,结合未被平衡的超高限值要求对曲线半径调整量进行限制。根据TG/GW 102—2019《普速铁路线路修理规则》,未被平衡欠超高不应大于75 mm,困难情况下不大于90 mm;未被平衡过超高不应大于30 mm,困难情况下不大于50 mm。未被平衡欠超高及过超高计算式为
式中:Hc为未被平衡欠超高,mm;Hg为未被平衡过超高,mm;vmax为线路容许速度,km/h;R为曲线半径,m;H为实设超高,mm;vH为货物列车平均运行速度,km/h。
2)缓和曲线长度
缓和曲线长度的调整会导致其超高顺坡坡度发生变化,对行车安全性和旅客舒适性造成不利影响,因此,结合超高顺坡坡度要求对缓和曲线长度调整量进行限制。TG/GW 102—2019规定:vmax> 120 km/h时,顺坡坡度不应大于1/(10vmax);vmax≤ 120 km/h时,顺坡坡度不应大于1/(9vmax);困难条件下,可适当增大顺坡坡度,但vmax> 120 km/h时不应大于1/(8vmax),其他线路不应大于1/(7vmax)且不得大于2‰。
此外,为便于铁路工务部门日常线路养修管理,TB 10098—2017《铁路线路设计规范》给出的缓和曲线长度一般取10 m的整倍数。
3)圆曲线或夹直线最小长度
圆曲线或夹直线长度大小与线路养修工作量、行车平稳性和旅客舒适性密切相关。根据TG/GW 102—2019,圆曲线或夹直线最小长度应满足表1要求。
4)特殊地段调整量
为保证列车运行安全,应结合线间距、桥梁偏心、建筑限界,对重构设计线形平面位置进行合理限制,平面调整量须满足相关要求。
重构设计后,对于直线区段,当120 km/h <v≤160 km/h时相邻两线间距限值为4.2 m,v≤ 120 km/h时为4.0 m。其中v为设计速度。对于曲线地段,线间距应满足TB 10098—2017中的加宽要求。
线路平面调整时应对桥梁偏心情况进行改善,严禁造成桥梁偏心超限情况。TG/GW 103—2018《普速铁路桥隧建筑物修理规则》规定:运营桥上线路中线与梁跨设计中线的偏差,钢梁不应大于50 mm,圬工梁不应大于70 mm;行车速度大于120 km/h区段,钢梁、圬工梁均不应大于50 mm。
平面调整应对既有建筑限界不足地段进行改善。平面线形绝对位置应满足GB 146.2—2020《标准轨距铁路限界 第2部分:建筑限界》的相关要求。
2 平面线形重构设计模型
2.1 目标函数
实测线形和设计线形在平面上的差值即为平面调整量,该值表征了轨道由实际线形调整至设计线形的工程量,因此不同设计线形引发的线路养修工作量有所差异[9]。本文以所有测点平面调整量平方和最小作为设计目标,将圆曲线半径、前后缓和曲线长度作为优化参数,建立平面线形重构设计目标函数。表达式为
式中:l1为前缓和曲线长,m;l2为后缓和曲线长,m;Δti为测点i处平面调整量,mm;N为测点数量。
2.2 约束条件
结合现场实际应用情况及平面线形参数限制因素,建立三种约束条件。
1)无约束
平面线形重构设计过程中,曲线半径及缓和曲线长度以线路实际变形为准,不对其取值进行任何限制,仅需达到重构设计目标函数[式(2)]要求,即平面调整量平方和最小。
2)原始台账约束
平面线形重构设计过程中,曲线半径及缓和曲线长度按照原始台账进行控制。约束条件为:R、l1、l2分别等于原始台账中的曲线半径及前后缓和曲线长度。
3)多参数约束
平面线形重构设计过程中,根据平面线形参数限值要求,对曲线半径和缓和曲线长度进行适当调整,二者变化范围满足未被平衡欠超高、过超高及超高顺坡坡度的限值要求,同时考虑缓和曲线长度取10 m整倍数、最小圆曲线或夹直线长度及特殊地段调整量限制。约束条件为:①R在曲线半径上下限范围内取值(曲线半径上下限须满足欠超高及过超高容许值要求);②l1、l2均不小于缓和曲线长度限值(缓和曲线长度限值须满足超高顺坡坡度限值要求);③l1、l2均应取10 m整倍数;④圆曲线或夹直线长度不小于圆曲线或夹直线最小长度限值;⑤Δti小于测点i处平面调整量限值。
2.3 求解方法
采用原始台账约束条件时,直接根据原始台账中曲线半径及缓和曲线长度值求解调整量。
采用无约束条件和多参数约束条件时,通过枚举法对重构设计模型进行求解。具体步骤如下。
1)采用几何重心法计算曲线半径初始值,利用圆心到切线的垂向距离与初始半径的差值,估算缓和曲线长度初始值[10]。
2)结合约束条件,确定曲线半径及缓和曲线长度的搜索范围及对应的迭代步长。其中,在无约束条件下,曲线半径及缓和曲线长度的搜索范围分别取[0,20 000] m和[0,300] m;在多参数约束条件下,曲线半径及缓和曲线长度的搜索范围基于实设超高值,根据未被平衡的欠超高、过超高及超高顺坡坡度限值计算得到。
3)在搜索范围内,采用枚举法计算不同曲线半径及缓和曲线长度组合条件下的平面调整量值及其平方和。采用多参数约束条件时,须判断各测点调整量大小是否满足限值要求,若不满足则对夹直线方位角或曲线参数进行调整,直至满足为止。
4)对比不同曲线半径及缓和曲线长度组合条件下的平面调整量平方和,选取平方和最小的一组曲线参数作为最终结果。
3 工程验证
选取国内一普速铁路上行线K1133+100—K1145+000区段,采用激光定位+惯性测量模式采集其轨道中线平面坐标[7],采样间隔为5 m。该区段共含有8条曲线,曲线参数原始台账见表2。
3.1 测量精度
为了验证激光定位+惯性测量模式的平面测量精度,在上行线K1145+100—K1145+300区段进行两次测量,并计算平面偏差及两次测量平面偏差的较差,结果见图1。可知:两次测量平面偏差的较差不大,均在±1 mm以内,该模式的平面测量精度较优。

图1 激光定位+惯性测量模式的两次测量平面偏差对比
3.2 重构结果对比
分别采用无约束、原始台账约束和多参数约束条件,对K1133+100—K1145+000区段平面线形进行重构设计,得到其调整量及曲线参数。
3.2.1 调整量
三种约束条件下,线路平面线形重构设计后所得的平面调整量见图2。可知:三种约束条件的平面调整量在直线区段一致性较高,在曲线区段则存在较大差异。从平面调整量峰值来看,采用原始台账约束时最大,为155.07 mm;采用多参数约束时次之,为71.21 mm;采用无约束时最小,为59.93 mm。
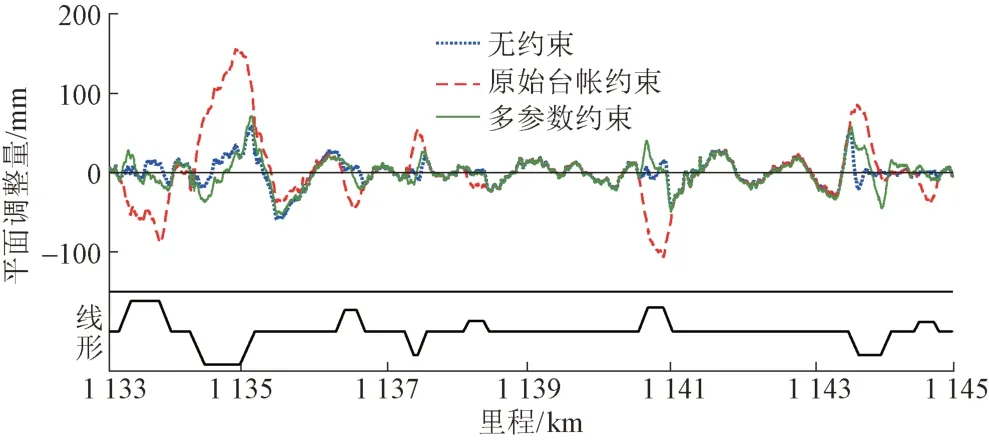
图2 三种约束条件平面调整量对比
为了对比三种约束条件平面调整量的分布规律,采用正态分布进行统计,并计算90%置信区间。首先以10 mm为一个区间长度,对各个区间内平面调整量数据个数进行统计,绘制柱状图;然后,为了进一步表达平面调整量的分布规律,绘制平面调整量的概率密度函数曲线,见图3。可知:采用无约束条件时平面调整量分布最为集中,其90%置信区间为[-26.56,27.27] mm;采用多参数约束条件时次之,其90%置信区间为[-30.58,29.62] mm;采用原始台账时平面调整量分布较为离散,其90%置信区间为[-65.48,70.15] mm。
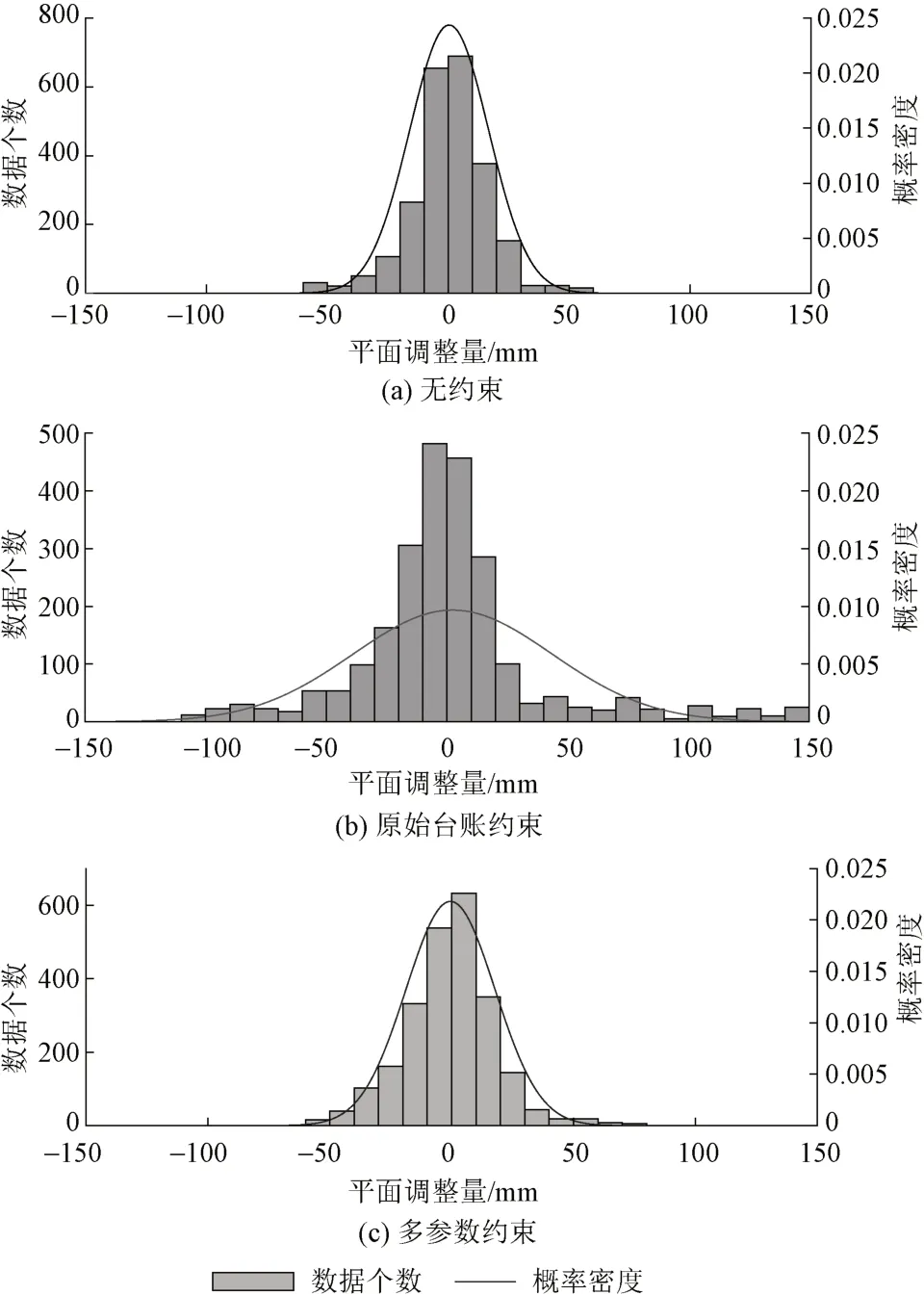
图3 三种约束条件平面调整量正态分布
3.2.2 曲线参数
三种约束条件下,线路平面线形重构设计后所得的曲线参数见表3。
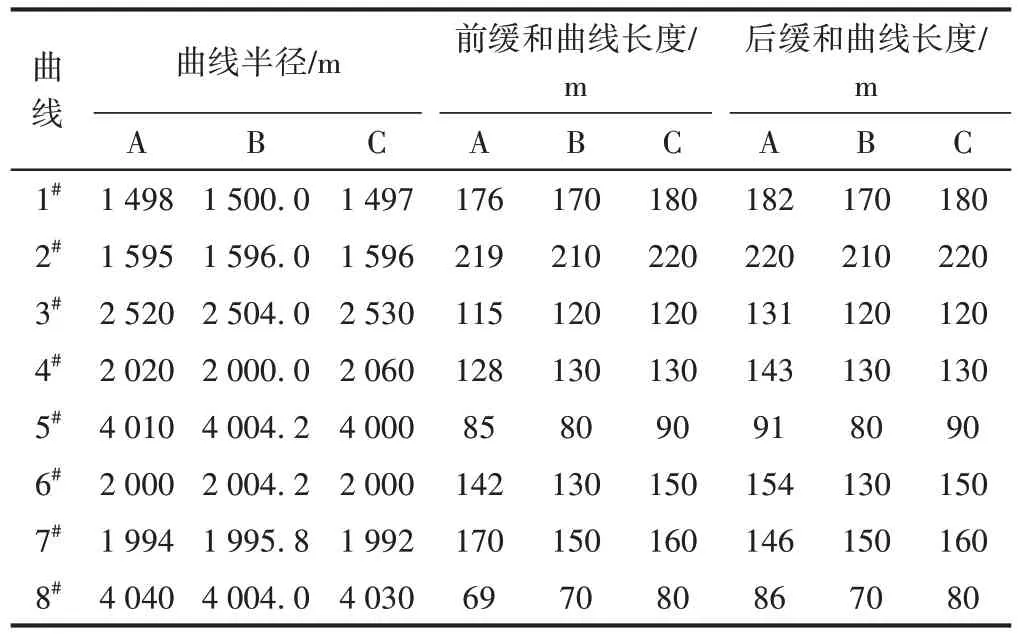
表3 三种约束条件曲线参数对比
由表3可知:重构设计后,采用原始台账约束条件所得的曲线半径及缓和曲线长度均与原始台账一致,而采用无约束和多参数约束条件时则发生了一定变化,其中曲线半径最大变化量分别为20、60 m,缓和曲线长度最大变化量均为20 m。采用无约束条件计算所得的部分缓和曲线长度不满足整10 m倍数要求,且前后不等长,不利于工务部门日常线路养修管理。
3.3 行车安全性
为分析三种约束条件下重构后的平面线形对行车安全性能的影响,根据表3,分别计算三种约束条件下曲线未被平衡欠超高、过超高及缓和曲线超高顺坡坡度,并通过车线动力分析模型计算车体动力响应[7]。
3.3.1 曲线欠超高和过超高
采用三种约束条件重构后的平面曲线,其欠超高和过超高见图4。可知:三种约束条件的曲线欠超高和过超高均满足TG/GW 102—2019的限值要求,且三者相差不大,不同约束条件的欠超高最大差值仅为4.40 mm,过超高最大差值仅为2.47 mm。
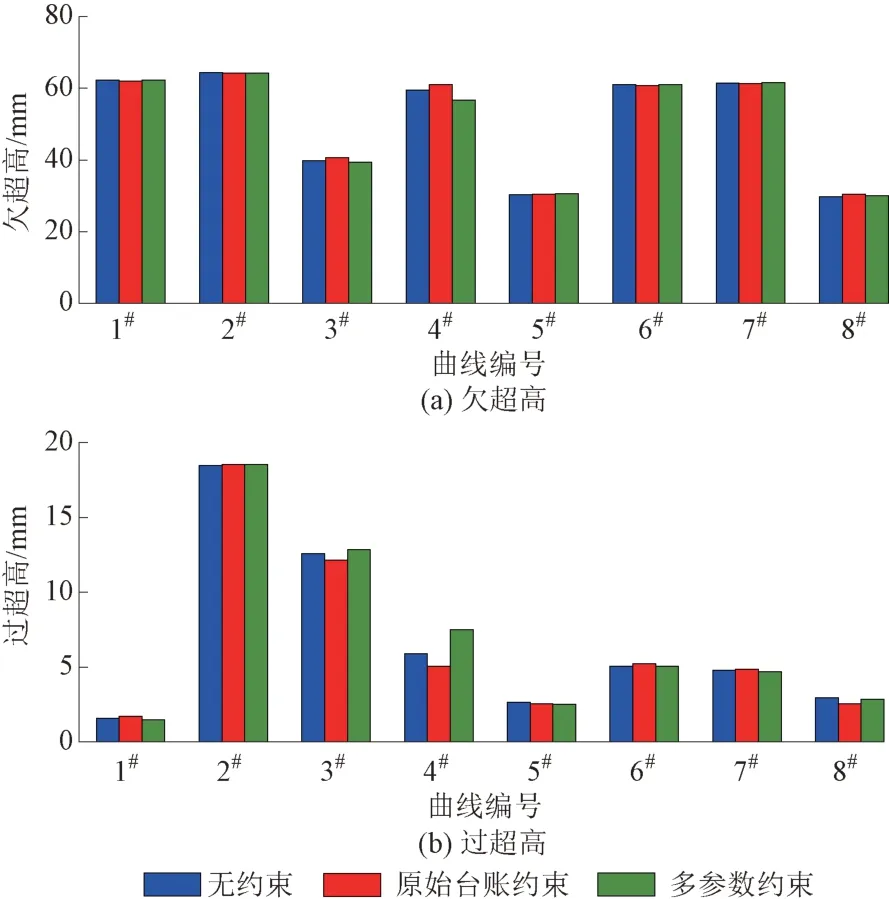
图4 曲线欠超高和过超高
3.3.2 缓和曲线超高顺坡坡度
采用三种约束条件重构后的平面曲线,其前后缓和曲线超高顺坡坡度见图5。可知,三种约束条件的顺坡坡度均满足TG/GW 102—2019的限值要求,且三者相差不大,不同约束条件的前缓和曲线超高顺坡坡度最大差值仅0.09‰,后缓和曲线超高顺坡坡度最大差值仅0.12‰。

图5 前后缓和曲线超高顺坡坡度
3.3.3 车体动力响应
利用车线动力分析模型,仿真计算列车在采用三种约束条件重构后的平面曲线上运行时的车体动力响应。车辆模型由车体、构架、轮对和轴箱多个刚体组成,共50个自由度,各刚体间通过一系和二系悬挂相连。车轮采用LMA型车轮踏面,钢轨采用60 kg/m钢轨。采用Kalker简化滚动接触理论计算轮轨蠕滑力和蠕滑力矩,采用FASTSIM算法计算轮轨作用力。由于仅对比不同平面线形参数下车体动力响应的差异,将纵断面设定为一平坡。采用实测线路不平顺作为系统激励,车辆运行速度为160 km/h,车体横向、垂向振动加速度分别采用0.5 ~ 10 Hz带通滤波和20 Hz低通滤波处理。
列车在采用三种约束条件重构后的平面曲线上运行时,车体横向、垂向振动加速度最大值见图6。可知,对于三种约束条件,车体横向、垂向加速度均满足TG/GW 102—2019中的日常保持标准,且相差较小,最大差值分别为0.02、0.01 m/s2。

图6 车体振动加速度
4 结论及建议
本文结合相关规范要求系统梳理了普速铁路平面线形参数限制因素,以整体平面调整量平方和最小为平面线形重构设计目标函数,对比分析了无约束、原始台账约束和多参数约束条件下平面调整量、曲线参数和行车安全性的差异。主要结论如下:
1)采用无约束条件所得平面调整量最小,最大值为59.93 mm,90%置信区间为[-26.56,27.27] mm,但所得缓和曲线长度非10 m的整数倍,不利于工务部门日常线路养维管理;采用原始台账约束条件所得平面调整量最大,其最大值为155.07 mm,90%置信区间为[-65.48,70.15] mm;采用多参数约束条件所得平面调整量大小适中,其最大值为71.21 mm,90%置信区间为[-30.58,29.62] mm。
2)从曲线欠过超高值、前后缓和曲线顺坡坡度及车体横、垂向加速度来看,三种约束条件下所得结果基本一致,且均满足规范限值要求。
3)采用多参数约束条件所得平面线形既可达到现场工程量较小,又可满足曲线半径、缓和曲线长度和行车安全性要求,其重构设计结果最优。因此建议在普速铁路数字化捣固方案设计中,采用多参数约束条件对平面线形进行重构设计,在规范要求基础上对曲线半径和缓和曲线长度进行适当调整,以达到在保证行车安全的同时有效减小工程量的目的。本文研究结论可为我国普速铁路数字化捣固方案设计提供参考。

