铜-铝电磁脉冲焊接界面形成过程的原子扩散行为
李成祥,许晨楠,周言,陈丹,米彦
(重庆大学,输配电装备及系统安全与新技术国家重点实验室,重庆,400044)
0 序言
铜、铝均具有其独特的材料性能,两者可靠连接可充分发挥各自优势,在工业制造中的应用愈加广泛,如电动汽车锂离子电池铜极耳与铝合金盖引出极的连接等.电磁脉冲焊接(electromagnetic pulse welding,EMPW)是一种适用于铜、铝连接的先进制造技术.与激光焊、爆炸焊等技术不同,EMPW 通过高压放电产生的电磁力作为驱动力,在微秒级时间内可将焊接飞板(动力板) 加速至600 m/s~ 800 m/s,使其与焊接基板(待焊接板)发生猛烈碰撞,可忽略异种金属间不同物化性质差异实现连接,且无飞溅、热影响区,具有快速、环保和安全等优势,在航天飞机制造、车辆生产、印制电路板焊接等领域具有极大的应用潜力[1-3].EMPW 界面结合机制关系着焊接机理的阐明及效果的调控,一直以来受到了国内外学者的广泛关注.
EMPW 过程存在高速撞击产生的塑性变形以及高速撞击和涡流热效应导致的局部升温混合作用[4-6].对于EMPW 界面的结合机制,Li 等人[7]认为界面纹波是由局部熔融形成的中间层和固态键合形成的非晶相扩散层导致.Gobel 等人[8]发现当界面呈纹波状时,未见明显的扩散层,但存在金属间化合物聚集在熔融区域,得出沿界面的相形成和结合过程发生了局部熔化.然而,也有学者观测到EMPW 界面存在扩散层及机械咬合区域,未观测到金属间化合物,且扩散层中存在非晶相和多孔组织[9-12].因此,目前关于EMPW 界面结合机制主要存在3 种观点:①结合界面处发生原子扩散从而实现连接;②界面连接是一种宏观的机械咬合,即材料发生塑性变形实现连接;③EMPW 是一种熔化焊连接,结合界面处出现了局部熔化区.
尽管上述研究促进了对EMPW 界面结合机制的认识,但针对EMPW 过程中的原子扩散行为的研究尚不完善,且界面形成是1 个动态过程,不同阶段的原子扩散行为的差异不能忽略.与此同时,原子扩散是金属焊接过程中的重要物理现象之一,对于揭示EMPW 界面结合机制具有重要意义.为此,针对铜-铝EMPW 过程中的原子扩散行为及其界面结合机制开展研究.运用分子动力学模型结合EMPW 的动力学过程对铜-铝EMPW 典型界面(平直界面与涡旋界面) 对应的不同阶段原子扩散行为进行研究,并通过EMPW 试验验证.文中对EMPW 界面形成过程中的界面结合机制进行了原子层面的深入研究,可为EMPW 机理的阐明、焊接效果的调控提供科学依据与理论基础.
1 试验和模拟方法
1.1 材料预处理
EMPW 试验样品的材料采用1060 铝及T2铜,切割成几何尺寸均为100 mm × 50 mm ×1 mm 的板件.其中,铝板作为飞板,铜板作为基板.试验前,采用酒精将焊接面超声波清洗3 min,并通风干燥.
1.2 分子动力学模型
1.2.1 模型构建
该文采用LAMMPS 软件构建分子动力学模型[13].在分子动力学中,单个原子的运动状态可通过对牛顿运动方程积分获得.其中,牛顿第二定律的微分方程为
式中:mi是原子的相对原子质量,ri是原子的空间位置矢量,t是模拟的时间,V(r1,r2,···,rN)是原子的势函数.势函数被用来表示原子间的相互作用.嵌入原子势通常被用于金属体系当中,其函数形式[14]为
式中:ϕ是冲击势,为原子间的排斥作用;F是吸引势,为嵌入到电子气中的原子所受到的力;ρ是原子所处位置ri处的电子密度函数.
分子动力学模拟过程中,原子间的相互作用采用Cai 等人[15]得出的铜和铝的嵌入原子合金势,模拟步长设置为1 fs 进行加载、卸载、冷却3 个阶段的模拟.如图1 所示,首先建立铜板和铝板区域,铜板范围为(0~ 3.5) nm3× (0~ 3.5) nm3× (−27.5~ −1.5) nm3,包含28 800 个原子;铝板范围为(0~ 3.5) nm3×(0~ 3.5) nm3× (1.5~ 27.5) nm3,包含20 736 个原子.将两块板件的x-y表面设置为周期性边界条件,用于模拟无限表面以消除x-y方向的尺度效应,并将z方向设置为自由边界条件.铜板、铝板之间用3 nm 真空隔开,其间距远大于势函数的相互作用范围,相互不会造成影响.两板边缘分别固定5 层原子,达到碰撞固定的作用.最初整个系统采用Nose-Hoover 恒温器在25 ℃、零外压的定温定压(constant pressure temperature,NPT)系综下给予服从麦克斯韦速率分布的初速度进行弛豫.然后,给予铝板(飞板)一个初速度使两板件发生碰撞,原子的牛顿运动过程采用蛙跳法进行积分,在铝板固定层速度达到零时停止运动.再使该系统在微正则(micro-canonical,NVE) 系综下弛豫1000 ps 完成加载阶段.保持NVE 系综的平衡温度不变,在该温度、零外压的NPT 系综下弛豫1000 ps 完成卸载阶段.最后在NPT 系综下冷却到25 ℃室温,完成冷却阶段.

图1 分子动力学模型Fig.1 Molecular dynamics simulation model
1.2.2 扩散层计算公式推导
扩散系数与位移有一定的相关性.可以根据爱因斯坦扩散定律,将扩散系数表示为
式中:N是系统的维数.该文只考虑z方向上的扩散,因此取N=1,即均方位移(mean square displacement,MSD) 函数LMSD曲线斜率的一半为扩散系数.
为了更深入地理解铜-铝EMPW 过程中的原子扩散过程,该文提出一种基于LAMMPS 模拟的混合计算方法计算扩散层厚度.在等温条件下,当系统达到平衡时,铜和铝的规律扩散过程符合经典扩散方程,可以表示为
式中:n为原子浓度,t为扩散时间,D为扩散系数.式(4)包含的一个常规解为式中:N为扩散物质量,x为扩散距离.
该解与高斯密度分布函数的形式相似,相应的平均值为μ=0,方差为在扩散当中,通常将浓度超过5%的区域定义为扩散层.且对于高斯密度分布函数,其均值前后2 倍方差的面积为95%,即
所以得出扩散厚度计算公式为
由于实际焊接情况的扩散现象不够明显,所以该文模拟了1 组较大碰撞速度下的扩散过程以验证所推导的式(7)的准确性.模拟过程中,设置纵向速度vz=1 800 m/s,横向速度vx=800 m/s,原子均方位移如图2 所示.
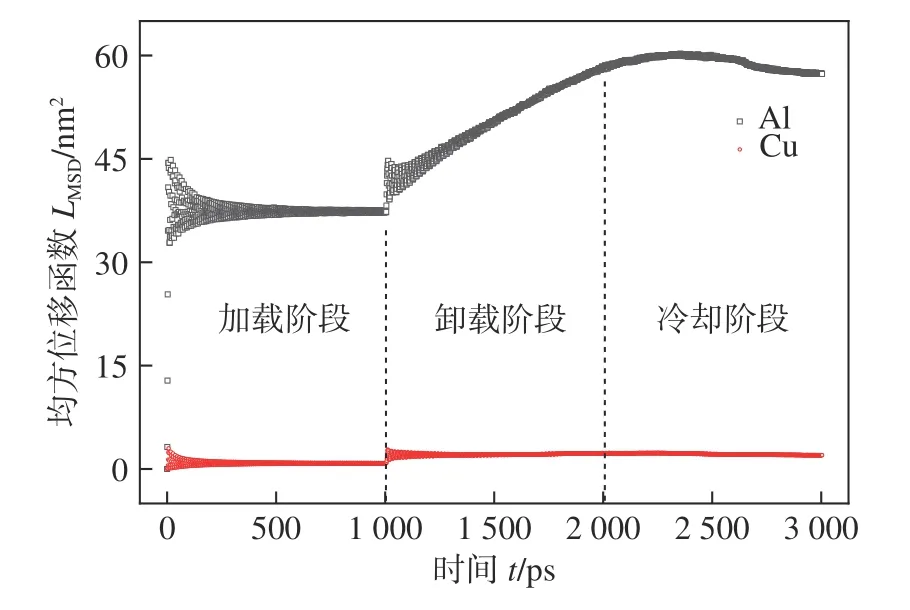
图2 EMPW 界面的原子均方位移Fig.2 MSD of EMPW interfacial atoms
均方位移函数能够表征原子的位移程度,当曲线上升时说明原子产生了位置移动,在宏观上表现为元素的扩散;当曲线保持在一定数值,或产生震荡时说明原子在自身位置震动.扩散几乎发生在卸载阶段,这是由于在相同的温度下加载阶段压强较大,Al 的熔点随着压力的增加而显著增加.此时整个系统仍保持固态,在加载阶段没有发生明显的扩散.而在卸载阶段,一旦系统压力被卸载,Al 的熔点降低,系统就会迅速熔化而发生明显的扩散.可以计算得出扩散系数分别为DAl=6.200 0 nm2/ns,DCu=0.120 4 nm2/ns.根据式(7)可以计算得出扩散厚度x=8.024 4 nm.通过从LAMMPS 输出文件提取原子的坐标信息也可以计算出扩散层的厚度,图2 中EMPW 界面的原子均方位移对应的原子分布曲线如图3所示.同样以浓度超过5%的区域作为扩散层,其扩散层厚度为8.24 nm,与计算结果基本一致,从而验证了式(7)的准确性.
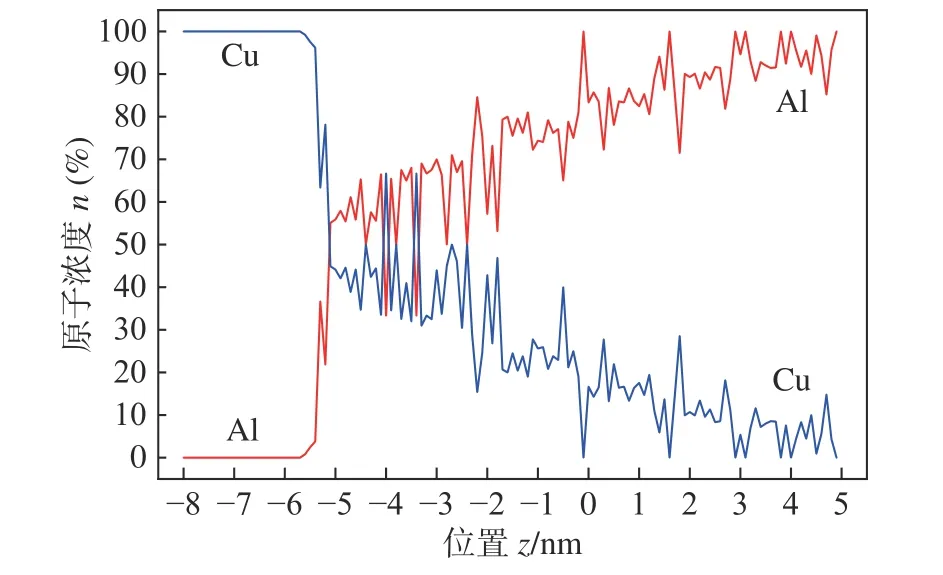
图3 EMPW 界面的原子分布曲线Fig.3 Distribution curves of EMPW interfacial atoms
1.3 EMPW 综合试验平台
该试验采用的EMPW 综合试验平台如图4 所示,它由EMPW 装置WD-28 和高速观测系统组成.

图4 EMPW 综合试验平台Fig.4 EMPW comprehensive test platform
WD-28 装置主要由高压电源、充放电开关、储能电容器组和焊接线圈组成,其控制信号由现场可编程逻辑门阵列产生,可产生0~ 6 μs 的可调脉冲信号,控制放电开关的导通.试验中,采用尺寸为110 mm × 10 mm × 8 mm 的I 型焊接线圈.铝板和铜板间放置两个2 mm 厚的绝缘垫片.试验中,使用Phantom V710 高速摄像机捕获焊接过程中飞板的动力学过程,该相机具备200~500 mm 变焦Nikon AF-S 200-500 mm f 5.5E ED VR 镜头.高速摄像机的同步触发装置与示波器相连接,当示波器检测到电压、电流信号时会自动触发高速摄像机进行拍摄.采样频率设置为610 000 帧/s,采集分辨率为192 × 24.在该采样频率下曝光时间极短,再加上间隙内光线微弱,因此采用LED 灯作为背光源进行补充照明.
1.4 微观结构表征方法
将焊接后的铜-铝EMPW 接头试样切割成1 mm 薄片进行磨样处理,并用Leica EM RES102离子减薄仪抛光.之后利用FEI Quanta 3D FEG 聚焦离子束制备样品,采用FEI Talos F200S G2 场发射透射电子显微镜对结合界面微观结构进行观测.
2 试验结果与分析
2.1 飞板的运动速度及EMPW 界面形成过程
根据该课题组前期研究可知,当放电电压为15 kV、铝板与铜板之间间隙距离为2 mm 时,所获的EMPW 接头的力学性能具有更好的稳定性和优越性[16].因此,该文主要对该条件下的EMPW 试样进行详细研究.当放电电压为15 kV 时,设备输出放电电压和放电电流波形如图5 所示.由图5 可知,开关同步导通后,放电电流呈现出典型的衰减振荡波形,其周期约40 μs.在第1 个振荡周期内,放电电流达到最大值,约为300 kA.高速摄像机的所获图片结果如图6 所示,由图6 可以观察到EMPW 过程飞板的动力学过程.整个碰撞过程可以分为两个阶段:变形阶段和扩张阶段.当放电开关导通后,飞板在电磁力的驱动下产生塑性变形并向基板运动.由于板件是1 个平面结构,且板件中部受到的洛伦兹力高于板件边缘[17],所以板件中部在t=4.92 μs 时先与基板发生碰撞,板件边缘在t=13.12 μs 与基板相撞,这个阶段为变形阶段.当飞板与基板碰撞后,飞板在惯性与电磁力共同作用下继续紧贴着基板运动,碰撞点继续向外移动,这个阶段为扩张阶段.EMPW 板件运动参数如图7 所示,由运动过程可知,变形阶段以顶端运动的某1 点为参考,纵向移动速度可根据式vz=∇s/∇t计算得出.扩张阶段以顶端左侧运动的某一点为参考,横向移动速度可根据式vx=∇d/∇t计算得出,其纵向速度vz=vx/tanα,碰撞点移动速度即为纵向速度与横向速度的矢量和.当t=13.12 μs 时,计算得到纵向速度vz=608 m/s,飞板与基板的碰撞角度约为19°,其横向速度vx为208 m/s,则碰撞点移动速度为643 m/s.

图5 EMPW 设备放电电压和放电电流波形Fig.5 Discharge voltage and current waveforms of the EMPW equipment

图6 EMPW 板件动力学过程Fig.6 EMPW Plates dynamics process
此外根据图6,该文还计算了碰撞后不同时刻EMPW 界面的碰撞点移动速度与碰撞角度,如图8 所示.由图8 可知,碰撞点移动速度先增大后减小,碰撞角度一直增大.原因在于变形阶段结束后,洛伦兹力需要克服的板件变形抗力变小,铝板的速度得以进一步提升.铝板与铜板碰撞时,最大变形区域与焊接线圈之间的距离达到5 mm,铝板磁感应强度及感应涡流都会减小.因此随着扩张距离的增加,洛伦兹力继续减小,铝板的速度不断降低,直至0 m/s.铝板与铜板碰撞后,角度的变化并没有停止.铝板碰撞点的速度高于非碰撞区域的速度,因此,碰撞角度持续增大,直到铝板停止变形.典型的铜-铝EMPW 界面的形成过程,可以分为4 个阶段如图9 所示.

图8 碰撞过程的参数变化Fig.8 Parameters in the collision process
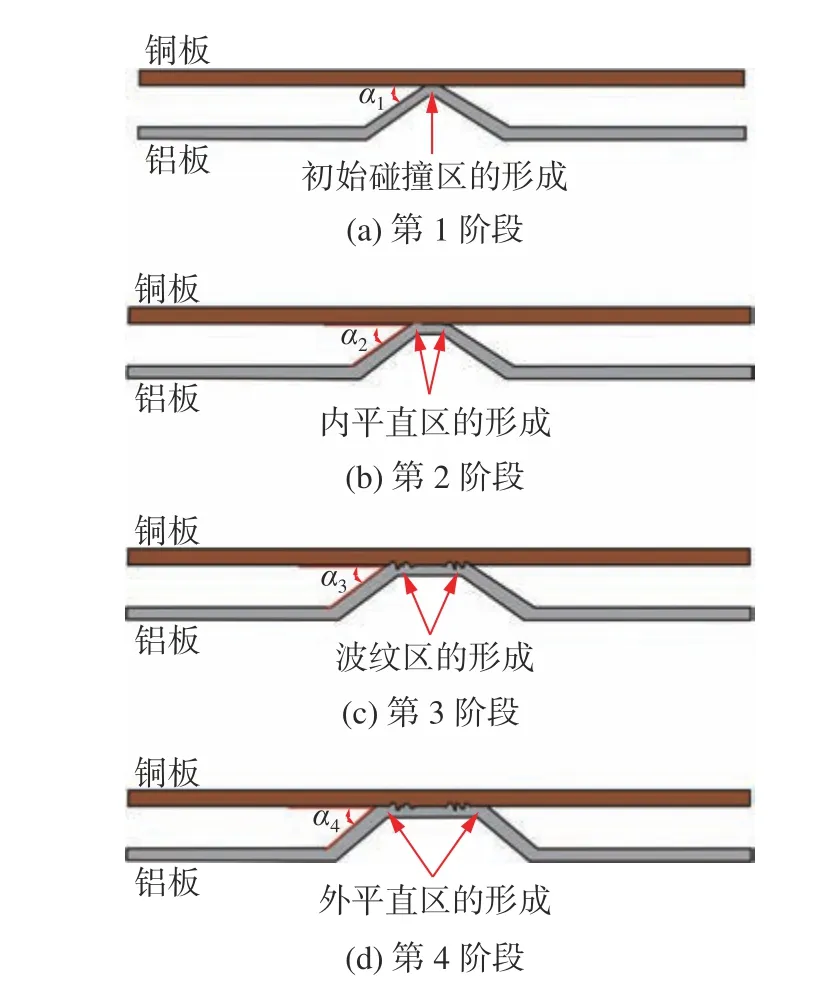
图9 EMPW 界面形成过程Fig.9 EMPW interface formation process.(a) the first stage;(b) the second stage;(c) the third stage;(d) the fourth stage
根据文献[16],在第1 阶段铝板在运动过程中存在“削顶”现象,因此在碰撞的初始时刻,铜板与铝板之间的夹角,即两者的初始碰撞角α1几乎为0º如图9 (a)所示.这样的碰撞角度使初始碰撞区易产生反弹,形成负位移,此阶段铜板与铝板未能形成可靠结合.在第2 阶段,碰撞角随碰撞点向外移动而逐渐增大,当满足金属射流形成的临界条件(碰撞角度达到α2),夹角处便会产生金属射流,连接界面中形成平直界面的焊接区如图9 (b)所示.当铝板与铜板碰撞后,由图8 的计算结果,铝板碰撞角(扩张角)是会不断增大的.根据文献[18],随着碰撞角的增大,波纹的波长和波幅先增大后减小.当碰撞角达到α3时焊接过程进入图9 (c) 所示的第3 阶段,其波长和波幅达到最大值.当碰撞角增大到不再满足波纹的形成条件时,连接界面的波纹不再产生,逐渐变得平直直至不能形成可靠焊接.因此,铜-铝EMPW 界面主要存在两种典型界面,即平直界面和涡旋界面.为进一步探究界面形成过程对原子扩散行为的影响,将不同典型界面形成过程的参数带入分子动力学模型中.
文中选取了图8中t为13.12 μs 和16.40 μs的时刻,所分别对应EMPW 的平直界面与涡旋界面形成条件.平直界面形成的纵向、横向碰撞速度分别为vz=608 m/s、vx=208 m/s,涡旋界面形成的纵向、横向碰撞速度分别为vz=765 m/s、vx=296 m/s.此外,文中还采用高速摄像机拍摄了放电电压为12~ 14 kV 时的焊接过程,得到4 组包含对应的放电电压下内平直界面形成区对应的横向、纵向速度及碰撞角度等运动参数如表1 所示.随着放电电压升高,其碰撞瞬间的夹角度数几乎不变,横向速度及纵向速度均有一定程度的增加.

表1 不同放电电压下的运动参数Table 1 Motion parameters under different discharge voltages
2.2 扩散过程的分子动力学模拟
将计算得出的碰撞速度带入分子动力学模型之中,进行加载、卸载、冷却3 个阶段的模拟,以探究EMPW 界面原子扩散行为.将表1 中第4 组运动参数的碰撞速度带入1.2 小节所述的分子动力学模型之中,由LAMMPS 输出系统文件得到EMPW界面平均温度和压强等热力学参数的变化.其中加载阶段整个系统的热力学参数变化如图10 所示.由加载阶段整个系统的温度和压力可知,随着系统动能转化为内能涡旋界面温度在接近5 ps 的时间内急剧上升至220 ℃,经过撞击后整个系统温度发生一定程度的波动,约500 ps 后基本平稳维持在185 ℃左右如图10(a) 所示.如图10(b) 所示涡旋界面的压强也在最初急剧上升至9.7 GPa,之后在8.8 GPa 左右保持稳定.而平直界面的温度和压强较涡旋界面稍低,分别维持在145 ℃和6.3 GPa 左右.部分局部区域的原子所获得的温度可能更高,这些原子能够在高温与压力的作用下获得足够的能量,使得内能得到提升,足以在下一卸载阶段克服势垒而发生扩散.在高温以及极大的压力作用下,异种金属原子间能够得到很好的接触而形成键合.扩散是物质中原子或分子的迁移现象.当部分原子获得足够能量而克服势垒迁移到其他位置时,在宏观上就表现为物质的扩散.从扩散的微观机制上来看,大部分学者认为磁场对于铜-铝这样的顺磁-抗磁合金系扩散起抑制作用,但上述观点都是在高温(500~ 1 000 ℃)、大时间尺度(h)下提出的.而对于EMPW 这种低温(低于250 ℃)短时(小于100 μs)过程,磁场并不会对分子间作用有显著影响,因此该模型并未考虑磁场对势函数的影响[19-20].为了更好的对原子的扩散运动进行分析,描绘了各阶段铜、铝原子的均方位移如图11 所示.
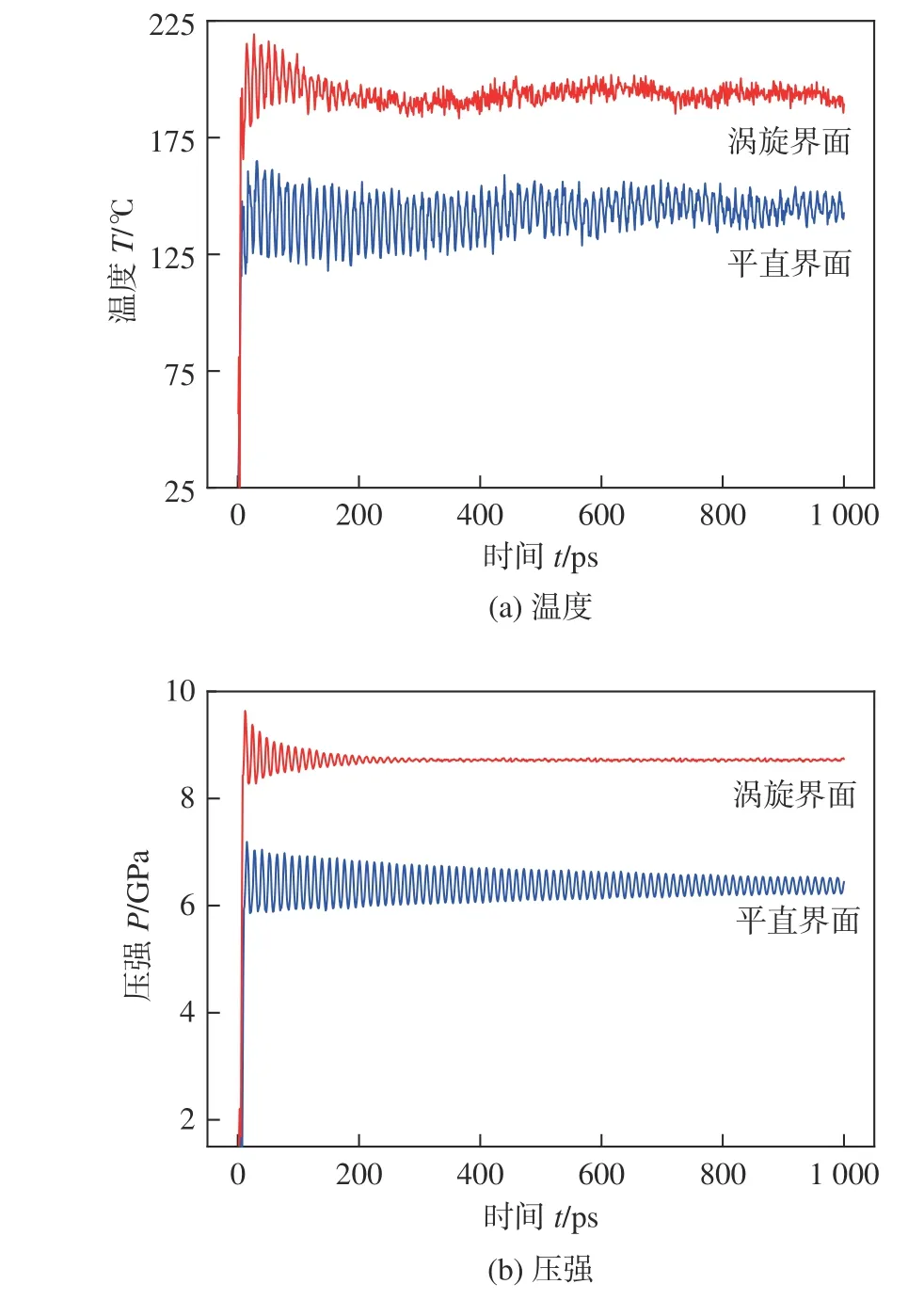
图10 加载阶段EMPW 界面热力学参数变化Fig.10 Thermodynamic parameters of EMPW interface during the loading stage.(a) temperature;(b)pressure
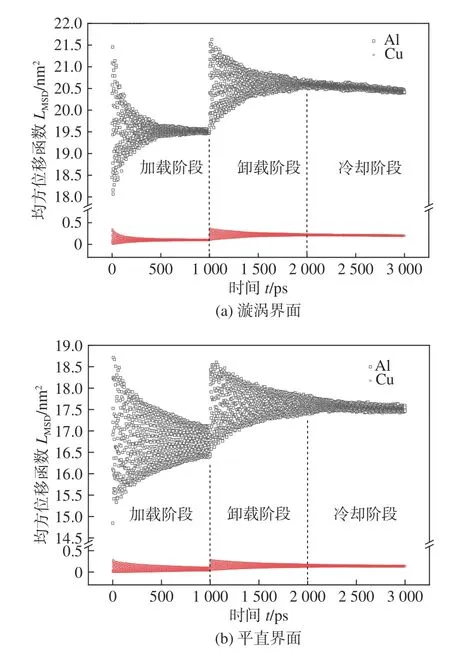
图11 EMPW 界面碰撞过程的均方位移Fig.11 MSD of EMPW interface collision process.(a)vortex interface;(b) flat interface
图11 中涡流界面模拟得出的均方位移值以及上升程度均大于平直界面结果.在加载阶段,铝板经过碰撞之后原子位置产生了一定程度的震荡,之后逐渐稳定,涡旋界面和平直界面的铝板均方位移值分别保持在19.4 nm2和16.5 nm2;铜板均方位移值在该阶段只有小幅度震荡,由卸载阶段所示,铝板和铜板的均方位移值均有一定程度的增加.冷却阶段的均方根位移曲线几乎保持原数值不变,原子没有发生扩散运动.由该结果分析可知,原子在加载阶段由于撞击能量转化为原子内力,在位置上发生剧烈震荡;进入卸载阶段后,铜和铝原子开始从界面两侧扩散,在给定速度条件下,铝的扩散率大于铜的扩散率.这些现象主要是由于铜的熔点(1 083 ℃)远远高于铝(660 ℃),因此在同样的温度下,铝原子的扩散速度更快.但扩散运动将很快结束并进入冷却阶段,整个焊接过程的扩散程度并不明显.
对图11 的原子均方位移进行线性拟合,计算得出平直结合界面铝板的原子扩散系数为3.079 8~ 7.6648 nm2/μs,铜板的原子扩散系数为0~ 0.3086 nm2/μs;涡旋结合界面铝板的原子扩散系数为7.682 1~ 14.4511 nm2/μs,铜板的原子扩散系数为0.187 3~ 1.0684 nm2/μs.根据文献[21]可知焊接中的卸载阶段大概可以持续5~ 10 μs,可以根据得到的扩散系数带入到式(7)中计算出实际焊接的平直、涡旋界面对应的扩散厚度为11.10~29.73 nm 和20.27~ 43.25 nm.加载阶段结束后平直界面模型结果如图12 所示.涡旋界面与其结果相似,其中红色为铝原子、蓝色为铜原子.在加载过程中,系统温度始终低于铝、铜的熔点,加载阶段无明显扩散.

图12 加载阶段结束的EMPW 界面模型Fig.12 EMPW interface model at the end of loading stage
明显的扩散主要发生在卸载阶段,图13 为卸载阶段结束后的模型,铜和铝的原子扩散深度较小,但依旧可以看出由于涡旋界面的碰撞速度以及产生的界面温度更高,涡旋界面的扩散程度相对更大.结合界面出现了铜原子向铝原子中扩散的现象,这是由于随着系统温度升高,铝中的键更容易断裂形成空位,铜原子容易向铝侧扩散.与之对应的界面结构分析结果如图13(b)所示,绿色表示面心立方(face centered cubic,FCC)结构,红色表示六方最密堆积(hexagonal close packed,HCP)结构,灰色为非晶态结构.由平直界面的结构分析结果可知,铜板仍保持原有的FCC 结构,但铝板由于横向速度的剪切应力作用出现HCP 结构与FCC 结构的共存结构,而界面位置呈非晶相结构,该结构更多的存在于铝板区域.

图13 卸载阶段结束的EMPW 界面Fig.13 EMPW interface at the end of unloading stage.(a) interface model;(b) interface structure
对于涡旋界面,铝板由于横向速度更高,受到更大的剪切应力并作用于铜板,所以铜板也呈现HCP 结构与FCC 结构的共存结构.且涡旋界面的铜板界面也出现了更多的非晶相.非晶相大多存在于铝板的原因在于铝板屈服强度低于铜板,更易在压力的作用下产生塑性变形,而铜板的屈服强度较高,所以在压力较大的涡旋界面才出现了更多非晶相.
2.3 放电电压对扩散厚度的影响
将不同放电电压下得到的内平直界面形成区的纵向和横向速度带入到分子动力学模型中进行模拟,通过绘制出对应的均方位移曲线拟合得出扩散系数,并根据式(7) 计算得出扩散厚度.如表2 所示,随着放电电压升高,铝原子扩散系数有一定程度增大,而铜原子扩散系数几乎没有变化.
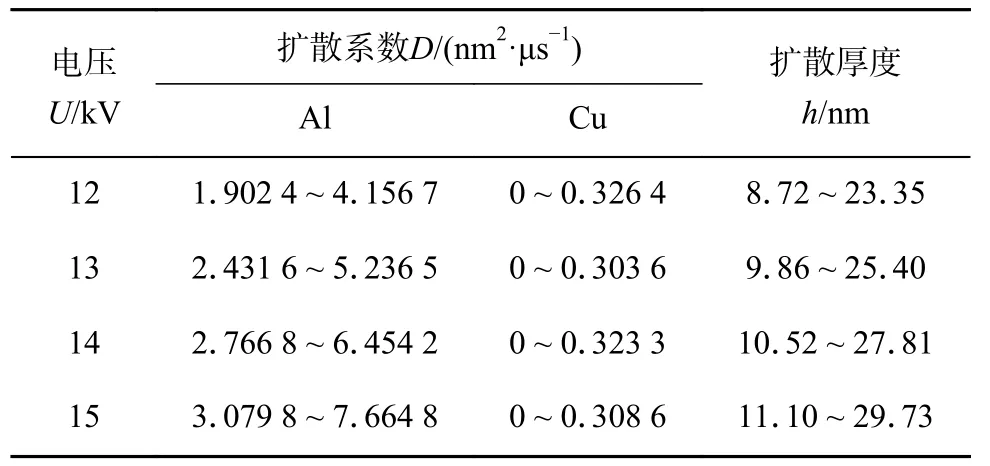
表2 不同放电电压下的扩散Table 2 Diffusion under different discharge voltages
这表明飞板(铝板)的速度提升能够有效提升其扩散行为,而基板(铜板)的扩散行为受飞板速度的影响较小.随着电压升高,根据公式计算得出的扩散厚度也相应变宽,但变化量均为纳米级,增幅较小,表明电压升高产生的速度增量仅能在较小范围内促进EMPW 过程的原子扩散行为.
2.4 结合界面的微观形貌
第4 组运动参数所对应的两种典型铜-铝EMPW 界面的微观形貌如图14 所示.

图14 典型铜-铝EMPW 界面Fig.14 Typical Cu-Al EMPW interfaces.(a) flat interface;(b) vortex interface
由图14 可知,平直界面只有小幅度的波纹起伏,可以近似视为直线;涡旋界面的接合面有明显的对侧金属凸起,且相互嵌入产生了卷曲的涡旋结构,形成机械咬合连接.
2.4.1 平直结合界面
对平直结合界面进行TEM 分析如图15 所示,图15(a)中部分区域存在非晶扩散层,未发现明显的金属间化合物.Al 和Cu 元素线扫描分析结果如图15(b) 所示,以原子浓度大于5%(点A、B) 的分布区域作为扩散层,其扩散厚度为13.78 nm,与计算得出的扩散层厚度一致.图15(c)为结合界面非晶层区域,非晶层厚度约6.64 nm,比扩散层稍窄,且在铝侧形成过饱和固溶体,与模拟的结构分析一致.由此前的压强和温度模拟结果图10 可知,在碰撞过程中界面温度迅速上升到165 ℃,升温速率达到1012 ℃/s,且未超过铝的熔点.
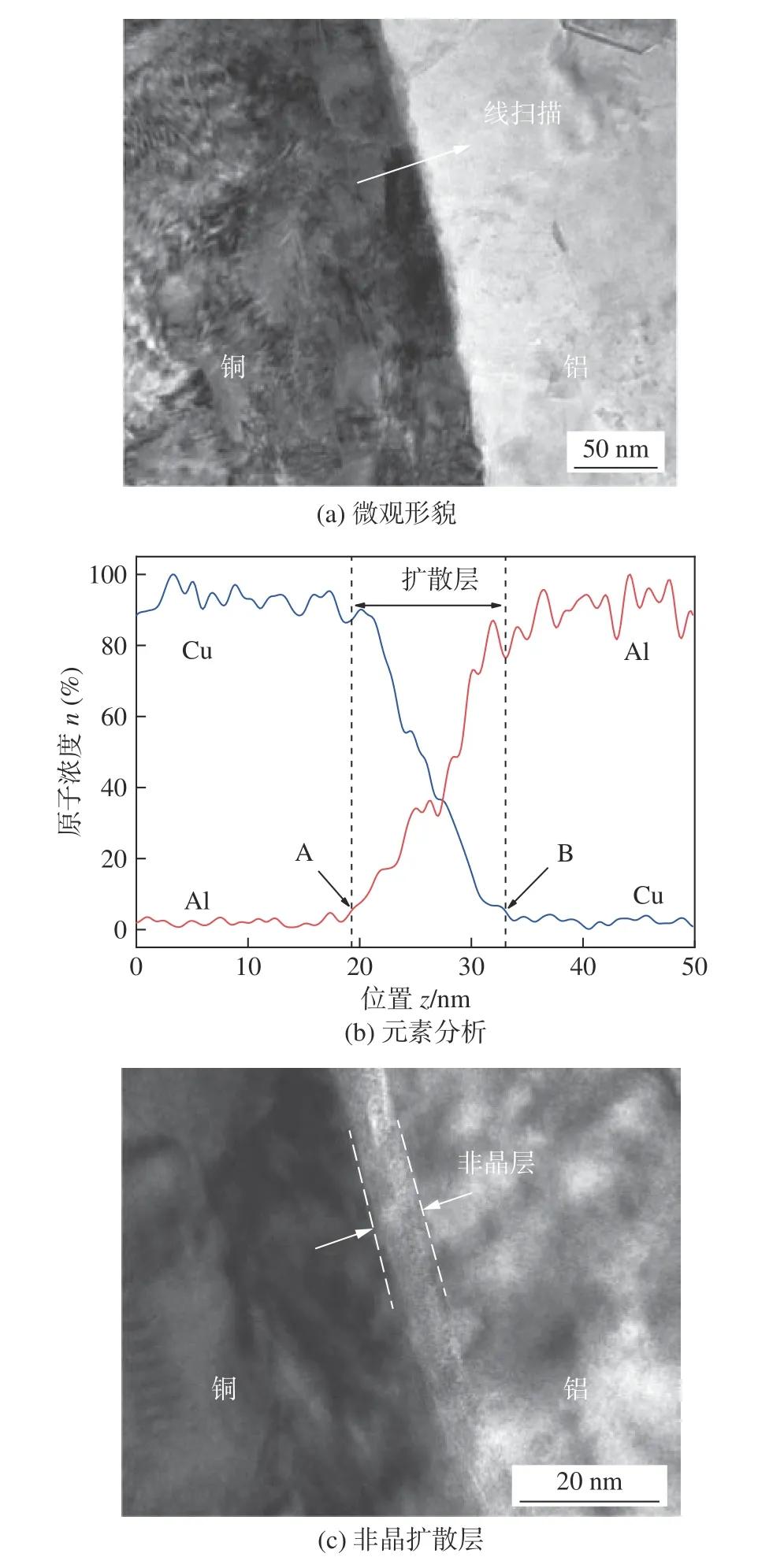
图15 平直界面透射电镜显微形貌Fig.15 TEM of flat interface.(a) microscopic morphology;(b) elemental analysis;(c) amorphous diffusion layer
这表明非晶化过程是固态转变,以及剧烈塑性变形引起的.压力达到最大值7.1 GPa,冲击压力的增加导致界面处塑性应变的增加,并且产生的相对较高的表面自由能可通过结构缺陷得到调节.即应变超过临界值时,晶体结构可能会坍塌并转变为非晶态结构,从而降低表面自由能.因此,温度的急剧变化以及界面较大的冲击压力为非晶层的形成提供了有利条件.
2.4.2 涡旋结合界面
对图14(b) 中涡旋结构中部的区域1 进行TEM 分析,分析结果如图16 所示.结合界面TEM微观形貌如图16(a)所示,主要元素的线扫描分析结果如图16(b)所示.由图16(a)可知,在涡旋的中间区域存在约100 nm 长,最宽处约宽23.31 nm 的非晶区域.涡旋界面受到的更大冲击压力使得其非晶区域宽度大于平直界面非晶层.对该区域以及涡旋结构的背部进行线扫描分析,结果如图16(b)所示,非晶区域只有极少量铝元素扩散,为富铜非晶相.此外,涡旋的背部扩散厚度为41.5 nm,扩散程度高于平直界面,与模拟结果一致.
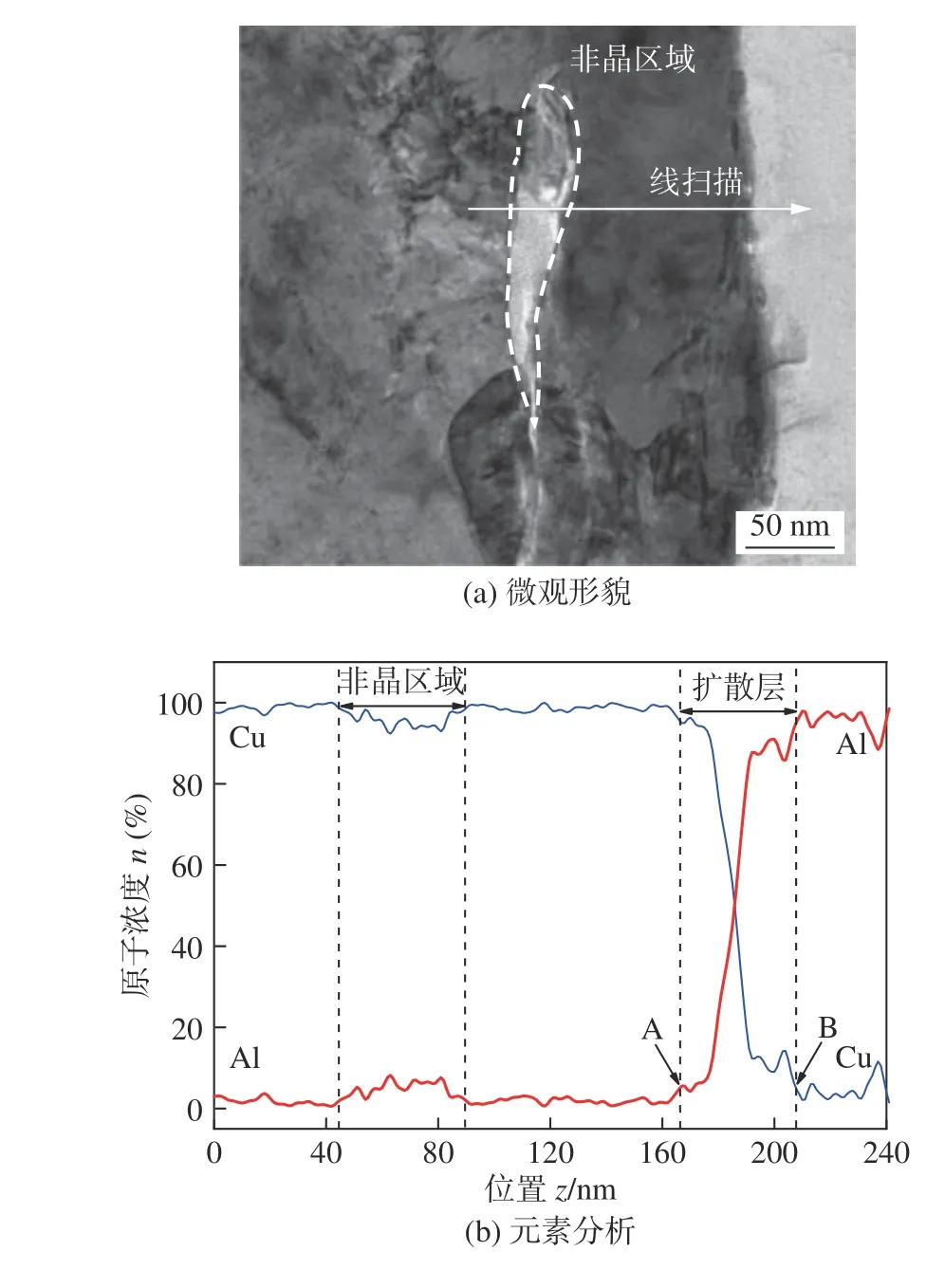
图16 涡旋结构中部TEM 分析Fig.16 TEM of the middle region of vortex structure.(a)microscopic morphology;(b) elemental analysis
图14(b)中区域2 标注的结合界面涡旋结构尾部的TEM 分析,分析结果如图17 所示.结合界面TEM 微观形貌如图17(a)所示.根据此处线扫描分析结果图17(b)可以看出,无元素平行区域,即无金属间化合物生成.其扩散层厚度为35.493 5 nm,也处于计算的扩散厚度范围内,说明模型能够较为准确地预测出EMPW 的原子扩散程度.此外,可以看出涡旋结构尾部图17(a)的铝一侧C 区域附近有明显的细小晶粒结构.细小晶粒结构集中在涡旋界面尾部的铝侧区域如图18 所示,且左边越靠近结合界面的区域,晶粒细化程度越高.晶粒的大小可以决定位错塞积群应力场到晶内位错源的距离.晶粒越小该距离越短,滑移就越容易从1 个晶粒转移到另1 个晶粒.因而,体积一定时,晶粒越细晶粒数量就越多,塑性变形时位向有利的晶粒数量也越多,塑性变形形变能较均匀的分散到各个晶粒上,金属的塑性也就越好.EMPW 过程中的猛烈撞击导致了界面处晶粒的细化,有利于材料发生塑性变形,而塑性变形产生的涡旋结构如同机械咬合结构,实现铜、铝之间的可靠连接.

图17 涡旋结构尾部TEM 分析Fig.17 TEM of the tail region of vortex structure.(a)microscopic morphology;(b) Elemental analysis

图18 涡旋结构尾部晶粒Fig.18 Tail crystal grains of vortex structure
3 结论
(1)构建分子动力学模型且推导了扩散层混合计算公式,并通过试验进行了验证,表明该文所构建的分子动力学模型能够较为精准地预测扩散层厚度.
(2)铜-铝EMPW 过程中碰撞点移动速度先增大后减小,碰撞角度不断增大,当碰撞速度较大时,有利于材料晶粒细化,产生塑性变形,从而在同一界面形成了平直-涡旋-平直的现象.
(3) EMPW 典型结合界面形成过程的不同阶段原子扩散程度不同,涡旋界面形成过程的原子扩散程度高于平直界面形成过程.原子扩散行为的差异由不同阶段碰撞点移动速度与角度产生.
(4) EMPW 过程存在原子扩散行为与相互咬合的机械结构,此外,结合界面未发现金属间化合物.因此,文中试验条件下界面结合机制主要为材料塑性变形引起的冶金结合和机械咬合共同作用.

