非高斯噪声下基于CKMC-CKF的发电机动态状态估计

赵志雷，黄继东，王义，杨志伟

(1.国能神东煤炭集团有限责任公司供电中心，陕西 榆林 719300；2.许继电气股份有限公司，河南 许昌 461000；3.郑州大学 电气与信息工程学院，河南 郑州 450001；4. 国网三门峡供电公司，河南 三门峡 472000)

随着相量测量单元(phasor measurement unit，PMU)的广泛应用，不同类型的状态估计(state estimation，SE)技术被用于跟踪电力系统的隐藏状态变量[1-3]。静态SE假定系统处于准稳态状态下，可以监测某时刻母线电压幅值和相位角。动态SE(dynamic state estimation，DSE)能实时监测系统的动态变化[4-5]。因此，DSE被广泛应用于电气设备控制方案的实现，如同步发电机的机电暂态跟踪。

对于DSE，近年来已提出了诸多经典卡尔曼滤波器(Kalman filter，KF)，如扩展KF(extended KF，EKF)[6]、无迹KF(unscented KF，UKF)[7]、容积KF(cubature KF，CKF)[8]及其扩展形式[9-10]，旨在准确跟踪系统的内部数据。鉴于非高斯过程的不确定性可能导致的偏差估计，文献[11]提出了一种简化的高斯综合EKF方法来处理非线性状态估计。考虑到线性化近似引起的EKF截断误差，研究人员又开发了几种无导数DSE方法。文献[12]基于平方根UKF和作用于测量状态估计的加权因子提出一种改进的方法，提高了状态估计的稳定性和鲁棒性。文献[13]引入了自适应UKF，同时监控集成电机变速器的控制输入和状态信息。文献[14]开发了基于变分贝叶斯的自适应CKF，可用于跟踪随机发生的注入攻击的状态。上述所提出的状态估计方法大多基于高斯噪声分布假设，在存在非高斯噪声的情况下，这些方法的估计性能可能会显著下降。

为了减轻测量函数中异常值的不利影响，如非高斯噪声、负载波动[15]等，研究者也提出了很多改进措施。为了降低恶意网络攻击导致的估计误差，文献[16]中构建了基于分布式压缩感知的估计策略。此外，作为信息理论学习(information-theoretic learning，ITL)的局部相似函数，熵包含了概率密度函数的高阶矩，在处理非高斯噪声假设时具有优异的特性。其中，基于最大熵准则的DSE算法被融合到EKF[17]、UKF[18]中，大幅增强了卡尔曼滤波器在非高斯噪声下的鲁棒性。然而，基于高斯核相关熵的最优核带宽(kernel bandwidth，KB)往往是通过大量计算和测试获得的，这在实际应用中限制了该方法的通用性。此外，高斯核函数在矩阵Cholesky分解中会出现奇异值[19]，严重影响了DSE的计算精度。

为了解决上述问题，提高传统DSE对非高斯噪声问题的鲁棒性，本文基于柯西核相关熵准则，提出一种基于柯西核最大相关熵(Cauchy kernel maximum correntropy，CKMC)的CKF算法(简称CKMC-CKF算法)。CKMC-CKF算法通过引入柯西内核优化准则，将CKF算法和CKMC准则相结合，可以有效抑制同步发电机模型中非高斯噪声对测量数据的不利影响。在IEEE 39节点系统上进行仿真分析，以验证CKMC-CKF算法在非高斯噪声条件下的跟踪性能。

1 发电机动态状态估计模型

实际电力系统的离散微分方程由状态变量和测量值2个时变离散非线性函数组成，采用改进欧拉法[19]实现，非线性函数的具体表达式为：

(1)

式中：φ(·)、h(·)分别为状态传播函数和状态测量函数；Xk、Zk分别为时刻k的状态向量和观测向量；uk为时刻k的输入向量；wk、vk分别为时刻k的状态噪声和测量噪声。

同步发电机是电力系统中关键设备之一，对其准确建模对电力系统的动态跟踪具有重要意义。本文采用同步发电机的四阶模型，比传统的二阶发电机模型更接近发电机的实际运行模式。发电机状态函数建立如下[20]：

δ=ω-ω0，

(2)

(3)

(4)

(5)

式中：δ为发电机的功率角；ω为电角速度，ω0为其初始值；ed、eq分别为d、q轴上的瞬时电动势(下标d、q分别表示d、q轴，下同)；KD为阻尼系数；Aj、Tm、Te分别为惯性常数、机械功率、电磁功率；Ufd为定子的励磁电压；xd、xq为同步电抗；x′d、x′q为瞬态电抗；Td0、Tq0为时间常数；id、iq为定子电流。

本研究中设置状态向量Xk=(δ，ω，eq，ed)T，输入向量uk=(Tm，Ufd，iR，iI)T，其中iR、iI分别为定子R轴和I轴上的电流。为了提高同步发电机的估计精度，采用四维量测量，发电机的测量函数设置为Zk=(δ，ω，eR，eI)T，其中：

eR=(ed+idxq)sinδ+(eq-idxd)cosδ，

(6)

eI=(eq-idxd)sinδ-(ed+iqxq)cosδ.

(7)

为便于求解，将式(6)、(7)表示为状态变量和输入变量的函数：

id=iRsinδ-iIcosδ，

(8)

iq=iIsinδ+iRcosδ.

(9)

2 基于CKMC准则的CKF鲁棒动态估计

2.1 CKMC

作为统计相似性的度量，相关熵可以由1对随机变量A和B定义[17]：

V(A，B)=E[κσ(A，B)]=

(10)

式中：V(A，B)为变量A和B的均值；E(·)为期望算子，κσ(A，B)为对应的Mercer核，σ为KB；fA，B(A，B)为A和B之间的联合概率密度函数。

由于样本的有限性，V(A，B)的近似估计

(11)

式中：N为样本总数；Ai、Bi为第i对随机变量。

在信息理论学习(information theory learning，ITL)中，高斯核通常被认为是相关熵的核函数。本文采用柯西核作为熵的核函数，与高斯核[16]相比，柯西核结构简单，对KB不敏感，避免了最优KB选择的大量测试，提高了计算效率[17]。柯西核函数定义为

(12)

式中：e=A-B，Cσ(e)为对应的柯西核。

通过最大化式(11)并结合式(12)，可以获得基于CKMC的目标函数

(13)

2.2 CKMC-CKF方法的工作机理

本文所提的CKMC-CKF是在传统CKF框架上进行改进，通过线性回归方程推导出2种加权局部相似度函数，并结合CKMC准则，利用固定点迭代法不断更新误差协方差矩阵，从而降低不良数据的权重，最终提高动态状态估计的精度和鲁棒性。具体原理包含如下过程：

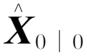
(14)

(15)

当k>0时，首先，根据球面径向容积法则，生成一组容积Sigma点：

(16)

j=1，2，…，2n.

(17)

(18)

式中：Xj，k-1|k-1为k-1时刻第j个Sigma点；Ij为单位矩阵；n为状态维度；Sk-1|k-1表示对矩阵Pk-1|k-1Cholesky分解。

(19)

(20)

(21)

(22)

(23)

Zi，k∣k-1=h(Xk，Xi，k∣k-1)；

(24)

(25)

(26)

式中：Xi，k∣k-1为Sigma点；Zi，k∣k-1为经量测方程传播后的Sigma点。

c)线性回归方程的推导。为了迭代计算出最佳的状态估计值，首先定义伪量测向量

(27)

将量测函数线性化近似，得到近似后的量测值

(28)

由式(1)、(28)，可得线性回归方程组

(29)

其中，

(30)

(31)

式(29)—(31)中：ηk为误差矩阵；Bp，k∣k-1、Br，k分别为Pk∣k-1、Rk进行Cholesky分解所得的分解因子。

基于式(13)，所提CKMC-CKF方法的目标函数可进一步表示为：

(32)

(33)

(34)

式中：eX，i、eZ，i为加权矩阵eX、eZ的第i个变量；m为量测信息的维度数。

柯西核相关熵采用2种加权相似函数对状态误差和量测误差进行修正，从而降低不良数据的权重。对式(32)求偏导，并且令∂JCKMC/∂Xk=0，可得：

(35)

进一步整理式(35)，利用量测量对预测后的状态值进行修正，得到状态量的最优估计形式为

(36)

其中：

(37)

(38)

(39)

(40)

(41)

最后，状态量后验误差协方差Pk更新为

(42)

基于CKMC-CKF的同步发电机DSE流程如图1所示，其中，t为内循环的时间变量，k为外循环的时间变量，ε为判断阈值。

图1 基于CKMC-CKF的同步发电机DSE流程Fig.1 Synchronous generator DSE flowchart based on CKMC-CKF

3 算例分析

3.1 算例设计与评价指标

在本节中，使用IEEE 10机39节点标准系统模拟电力系统的网络结构，其拓扑如图2所示。由于噪声分布的随机性，使用蒙特卡洛技术来模拟噪声的统计信息，并设置采样数N=200。假设系统在16-21线路处发生三相金属性接地短路，且当仿真进行到0.5 s时出现系统故障，经0.2 s后系统过渡至新稳态。其中，以稳态运行值作为状态变量的初始值，并且初始误差协方差设置为P0∣0=10-5I。此外，过程和测量的噪声协方差矩阵分别设置为10-5I和10-6I。本文以同步发电机Gen2为例，将CKF[8]、MCC-CKF[22]与所提CKMC-CKF方法进行比较，验证CKMC-CKF方法的有效性。

图2 IEEE 39节点系统Fig.2 IEEE 39 bus system

为了评估各种滤波方法对于发电机状态的跟踪效果，本文将平均绝对误差M和总体性能误差J作为评价指标对不同方法的估计结果进行量化分析，定义如下[17]：

(43)

(44)

3.2 KB测试

如文献[16]所述，相关熵中KB对状态估计的准确性具有决定性作用。具体而言，过大的KB可能无法抑制异常值，过小的KB可能导致收敛缓慢，因此KB的取值对于DSE的估计结果至关重要。为了验证所提方法在不同KB下的性能，本文所提出的CKMC-CKF算法在不同KB下的误差指标见表1。

表1 不同KB下CKMC-CKF的误差Tab.1 Errors of CKMC-CKF at different KBs

从表1数据可知，CKMC-CKF算法在不同KB下的估计误差没有太大差异。基于柯西内核损失准则的最大熵对KB的选择不敏感，在很大程度上避免了对最优KB的大量实验，从而提高了算法的通用性。为了便于后续研究，CKMC-CKF的KB设置为50。

3.3 噪声不确定性测试

由于实际电网中运行环境的时变性，噪声的统计特性在实际系统中会随着时间而变化[21]，因此，实际仿真中的系统噪声通常是未知的。为了验证所提方法在该工况下的有效性，假设系统的过程噪声协方差设为Qk=diag(10-3，10，10-1，10-1)，测量噪声设为Rk=diag(10-5，10-5，10-3，10-5)。

在该工况下，CKF、MCC-CKF、CKMC-CKF 3种方法的状态变量估计结果如图3所示。可以看出：当故障出现后，CKF对于同步发电机的状态跟踪出现了较大的估计偏差，精度下降严重；MCC-CKF对不确定的高斯噪声具有一定的抵抗力，但也因其对KB的依赖而受到限制。相比而言，CKMC-CKF具有良好的数值稳定性和对不同KB的不敏感性，因此其估计曲线最贴近系统的真实状态，状态估计的精度更高。

图3 噪声不确定工况下的状态估计Fig.3 State estimation under noise uncertainty

噪声不确定工况下CKF、MCC-CKF和CKMC-CKF方法的估计误差指标对比情况见表2。可以看出，与传统CKF和MCC-CKF相比，本文所提的CKMC-CKF方法误差最小，估计精度更高，对于不确定噪声的鲁棒性更强。

表2 噪声不确定工况下的估计误差指标Tab.2 Estimation error metrics under noise uncertainties

3.4 非高斯噪声测试

发电机动态估计模型中通常假设噪声为高斯白噪声，即噪声协方差是一个常数矩阵。在实际电力系统中，PMU采集的量测信息在传送至控制中心时，通信信道易遭受噪声污染，导致出现非高斯噪声，这会影响动态状态估计性能，降低滤波精度[22]。

为了验证所提方法在非高斯噪声下的滤波性能，假设量测方程中的噪声信号rk是由混合高斯函数表示的重尾噪声，即

(45)

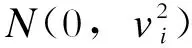
图4展示了v1=10-4、v2=10-6、θ=0.98时的状态估计情况。可见，当系统出现非高斯噪声时，基于高斯噪声假设的CKF方法跟踪速度大幅下降，与状态真实值具有明显的误差，跟踪精度较低，已经不满足动态估计的准确性和实时性要求；相比于CKF，MCC-CKF方法对非高斯噪声具有一定的鲁棒性，但是由于MCC准则基于高斯内核，对于非高斯噪声情形的估计误差仍然较大；CKMC-CKF方法与真实值更加接近，相比于CKF和MCC-CKF，估计精度分别提高了约78%和35%。这是由于CKMC-CKF方法将柯西内核作为相关熵的内核函数，既克服了KB选择复杂性的困难，也极大降低了非高斯噪声情形下发电机的估计误差。因此，该工况下CKMC-CKF方法具有最高的估计精度和最强的鲁棒性能，能够准确地跟踪发电机的状态。

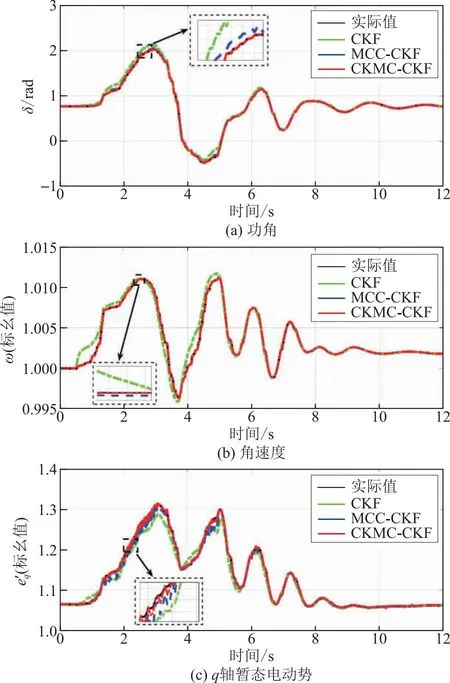
图4 非高斯噪声工况下的状态估计Fig.4 State estimation under non-Gaussian noise

不同滤波器在混合程度为θ=0.98、θ=0.95下的误差指标分别见表3、表4。可以看出，本文方法在非高斯噪声下估计误差最小，滤波性能最好。

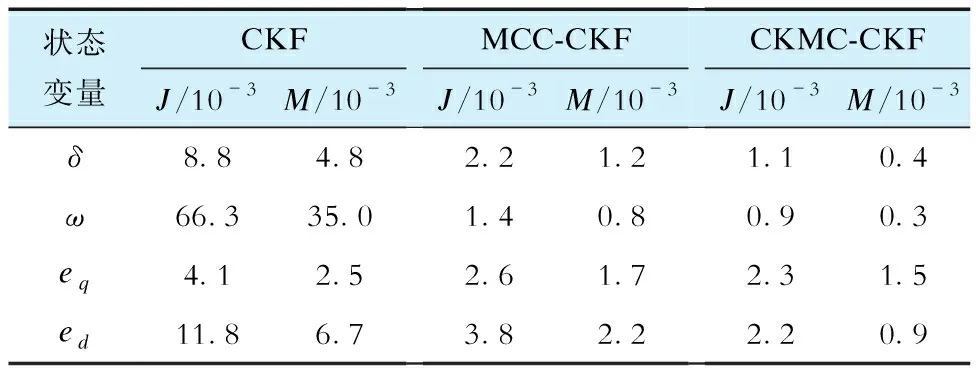
表3 非高斯噪声混合度为0.98时的误差指标Tab.3 Error metrics for non-Gaussian noise with mixing degrees θ=0.98

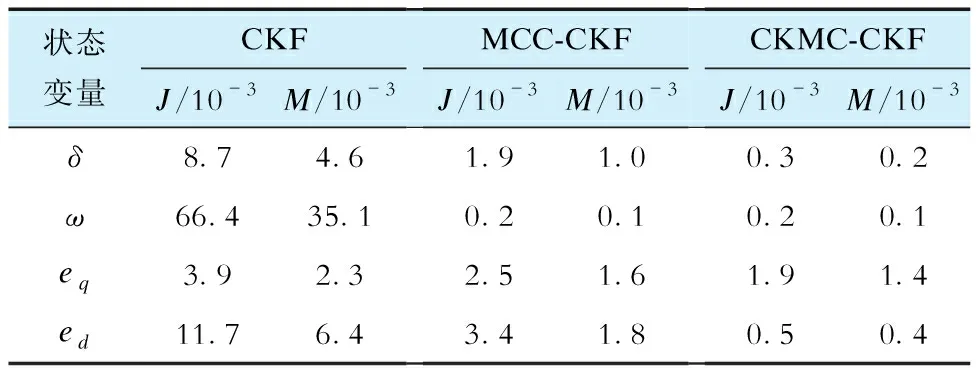
表4 非高斯噪声混合度为0.95时的误差指标Tab.4 Error metrics for non-Gaussian noise with mixing degrees θ=0.95

4 结论

针对电力系统中同步发电机动态状态估计中存在的非高斯噪声问题，本文提出了一种基于CKMC-CKF的发电机动态状态估计方法，主要结论如下：

a)利用柯西核作为相关熵的核函数，避免了最优KB选择的大量测试，提高了动态状态估计的计算效率；利用熵增益动态修正误差协方差，增强了状态估计的精确性。

b)通过在IEEE 39节点系统进行仿真分析可知，相比于CKF和MCC-CKF，所提CKMC-CKF方法在非高斯噪声环境下具有更准确的估计精度和更强的鲁棒性，可以有效地跟踪同步发电机的状态。

c)后续将进一步研究电力系统遭受网络攻击情况时，同步发电机的量测信息和状态估计问题。