有多少个三角形

◎叶杰平

街心广场里有一个地标建筑物，它的平面图是一个由很多个小等边三角形组成的大等边三角形（如右图），这个图中一共有多少个三角形？

解题思路

要求一共有多少个三角形，不仅要数出有多少个小的三角形，还要数出有多少个中的、大的三角形。然后，再算出它们的总数。怎样数才能不重复、不遗漏呢？

我们先假设图中最小的等边三角形的边长是1厘米，用列表的方法有顺序地进行分类画一画、数一数，就能准确地算出一共有多少个三角形。

先数一数边长为1厘米的正立和倒立的等边三角形各有多少个（如右图）。

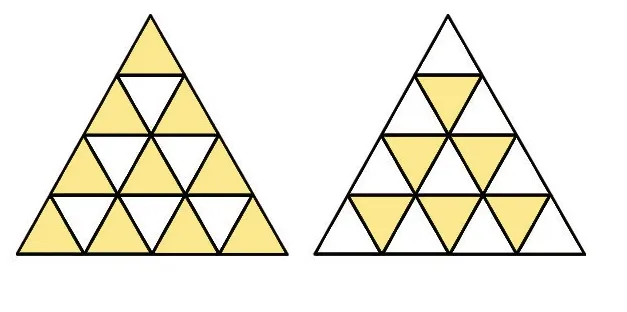
通过画一画、数一数，得出有10个正立和6个倒立的边长为1厘米的等边三角形。

再数出边长为2厘米的正立和倒立的等边三角形个数（如下图）。

通过画一画，数出6个正立和1个倒立的边长为2厘米的等边三角形。

然后依次数出边长分别为3厘米、4厘米正立和倒立的等边三角形个数（如右图）。

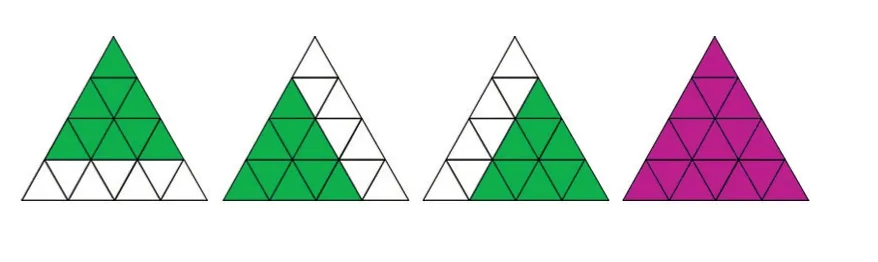
数出边长为3厘米的正立的等边三角形有3个，边长为4厘米的正立的等边三角形有1个，边长分别为3厘米、4厘米的倒立的等边三角形都是0个。

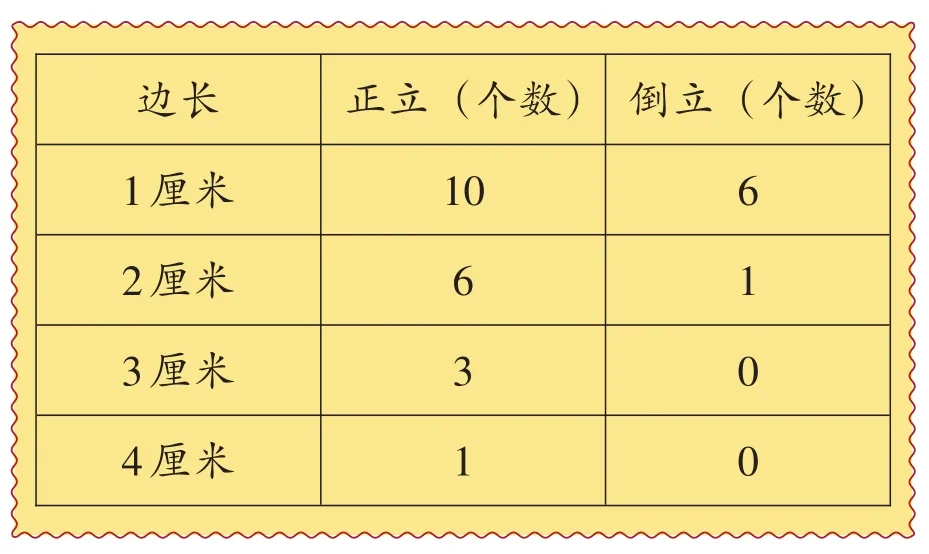
将各种大小的三角形列成表格进行统计。

最后把全部三角形的个数加起来，算出三角形的总个数是10+6+6+1+3+1=27（个）。

解题点拨

像这种数学问题，我们可以应用列表法来解决问题。通过画一画、分类统计的方法，把每一类的数量数出来，并填写在表格中，这样可以清晰地看到每一类的数量，使解决问题的过程更有条理性，使复杂的问题简单化，做到不重复、不遗漏，准确地解决问题。

练一练在右图中，大的正方形里有很多个小的正方形。请你动手画一画、数一数、列一列，算出一共有多少个正方形。