线圈电势求取过程中两种标注方法的比较

程小华

(华南理工大学电力学院,广东广州510640)

0 引言

《电机学》的交流电机绕组一篇在求线圈电势时,在线圈边电势参考方向的旁边,有些文献[1～10]标注线圈边电势的相量,有些文献[11、12]标注线圈边电势的瞬时值。为了引用方便,把前一种做法称为标注相量法,把后一种做法称为标注瞬量法。瞬量即瞬时值。本人认为：标注相量法是不妥的,标注瞬量法是恰当的。本文试图来论证这一点。

本文所称电势,乃电动势之简称。正向,正方向,参考方向,是一个意思。

1 两种标注法之简介

为了简便,又不影响说明问题,两种标注法各取一种文献为例加以说明。

1.1 标注相量法之简介

文献[2]p.192给出了匝电势计算图如图1(稍有改变,不影响实质)所示。

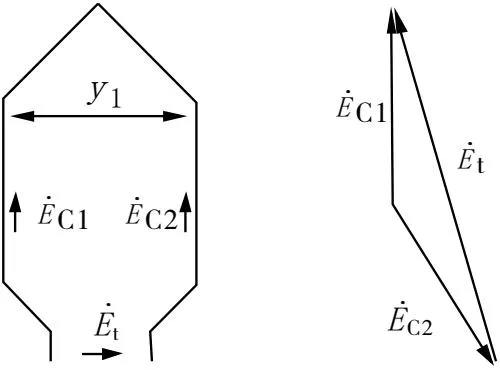
图1 匝电势计算图(文献[2])

同一页,文献[2]给出了匝电势计算式如式(1)(稍有改变,不影响实质)所示

(1)

1.2 标注瞬量法之简介

文献[11]p.150给出了短距绕组匝电势计算图如图2(稍有改变,不影响实质)所示。

图2 匝电势计算图(文献[11])

文献[11]先在p.144顶部给出了瞬时值表达式,如式(2)(稍有改变,不影响实质)所示

et=eA-eX

(2)

然后,在p.150底部给出了相量表达式,如式(3)(稍有改变,不影响实质)所示

(3)

2 两种标注法之本质区别

由上可见,两种标注法之本质区别在于线圈图上所标电势的不同：图1(a)上标注的是相量,图2(a)上标注的是瞬时值,即瞬量。其他的不同,譬如两个相量图即图1(b)和图2(b)中相量的相位、符号等不同,都不是本质性的区别。

两种标注法,最终都是用相量来计算匝电势。但是,文献[2]是一步到位,直接列出匝电势相量与两个线圈边电势相量之间的关系即式(1),而文献[11]是分两步走,先列出瞬时值表达式见式(2),再列出相量表达式见式(3)。

一个表达式与两个表达式的区别,正是线圈图上标注的本质区别导致的。

3 两种标注法之评价

文献[11]先列瞬时值表达式,再过渡到相量表达式,是必要,还是多余呢?本人认为是必要,而并非多余。换句话说,文献[2]“一步到位”(省去瞬时值表达式,直接列写相量表达式)是不妥的。理由如下。

3.1 正向的必要性

列写电路方程时,必须先假定一个正方向(简称正向),也叫参考方向,无论是交流电路,还是直流电路。原因在于,总有一些量,在求取之前,无法确定它们的方向,直流量是这样,交流量更是这样。因为交流量的方向,一直都是在变化着的。一言以蔽之,列方程,必先有正向。

3.2 正向的针对性

方程有两种,一种是瞬时值方程,一种是相量方程。那么,是不是有了正向,就可以列写相量方程或者瞬时值方程呢?本人认为,有了正向,可以列写瞬时值方程,而不能列写相量方程。原因是：正向是瞬时值的正向,而并非相量的正向。事实上,相量在旋转,方向无穷多,它没有正向概念。

因此,正向是针对瞬时值的,而非针对相量的。

3.3 正向名称的由来

变量的真实方向只有两个。因此,我们约定：当真实方向与正向(就是假定的参考方向)一致时,变量的前面加正号;当真实方向与正向相反时,变量的前面加负号。这样一来,当求解完成时,就可以反过来根据变量的正负,确定变量的真实方向。那就是：当变量数值为负时,表明该变量的真实方向与参考方向相反;当变量数值为正时,表明给变量的真实方向与参考方向相同。正因为如此,我们才把参考方向又称为正方向……变量数值取正时的方向。

3.4 相量与瞬时值的关系

由上可见,真实方向只有两个的时候,才可以有正向的概念。变量的真实方向,也就是瞬时值方向,只有两个,因此可以有正向概念。而相量是一个在相平面上旋转的复数,方向有无数多个,因而没有正向的概念。事实上,相量,并非一个真实存在的物理量,它是一个我们想象出来的代表真实物理量的数学量。相量配合时轴如图2(b)中的+j所示,可以得到真实物理量的瞬时值。具体来说就是：把相量向时轴投影,这个投影才是真实物理量的瞬时值。

3.5 相量与正向的关系

相量与正向没有直接关系,只有间接关系：选定正向后,可以得到瞬时值表达式;根据瞬时值表达式,可以得到相量表达式。换句话说,正向不同,相量的相位就不同。 原则上来说,瞬量的正向是可以任意设定的。但是,一般都遵循惯例。否则,将引起不必要的麻烦。在给一个线圈的两个线圈边电势标注正向时,惯例是两个正向取相同的方向。否则,将导致两个线圈边电势的相量同相位(整距时)或接近同相位(短距时)。这与直观相反。直观上,它们应该是反相,或者接近反相。人为制造理解上的困扰,不必要,不可取。譬如,文献[9]p114图4-11(a)把左线圈边之电势的正向标为向上,右线圈边之电势的正向标为向下;而图4-11(b)却把两个线圈边电势的相量画为接近反相。实际上,这种正向设定下,两个相量应该是接近同相。否则,根据KVL求线圈电势时,本来是相加,却变为相减了。

事实上,按文献[9]p114图4-11(a)标注正向时,两个线圈边的电势相量就不能画在同一个相量图上。因为正向不同时,瞬时值的表达式就不同,相当于计时起点不同;计时起点不同,相位关系就失去意义了。

直接给相量标注正向,如文献[1～10]所为,是没有意义的,是不恰当的。恰当的做法是,给瞬时值标注正向,得到瞬时值表达式之后,再过渡到相量表达式,如文献[11、12]所做的那样。在动手写这篇论文之前,我还以为所有的《电机学》都和文献[1～10]一样。翻阅手头所有的《电机学》文献后,才发现了文献[11、12]的不同。借助一句英文来描述这一现象,They make a difference. 文献[11、12]做法的严谨性,不由得令我肃然。

4 结语

本文比较了线圈电势求取过程中两种标注电势的方法,结论是：正向旁边标注电势的瞬时值是恰当的,标注电势的相量是不恰当的,理由有如下几点：(1)正向是针对瞬时值的,是针对瞬时值而假定的方向。(2)当瞬时值的真实方向与正向一致时,电势取正;相反时,电势取负。(3)瞬时值真实方向只有两种,一正一负,因而可以设定正向。(4)由于相量是旋转的复数,故相量的方向有无数种。因而,正向对相量没有意义。从而,就相量设定正向,或者在正向旁边标注相量,都是没有意义的。