穷根究底,“增解”何来?
2024-04-05 16:02:32赖呈杰林景芳
中学数学研究 2024年3期
赖呈杰 林景芳
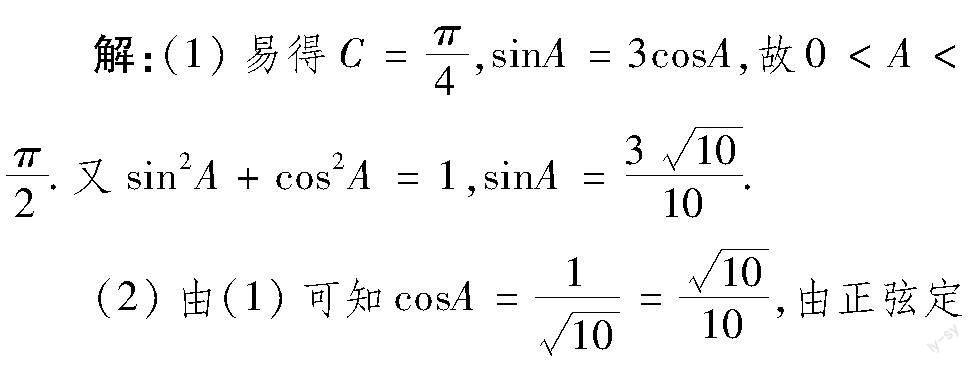
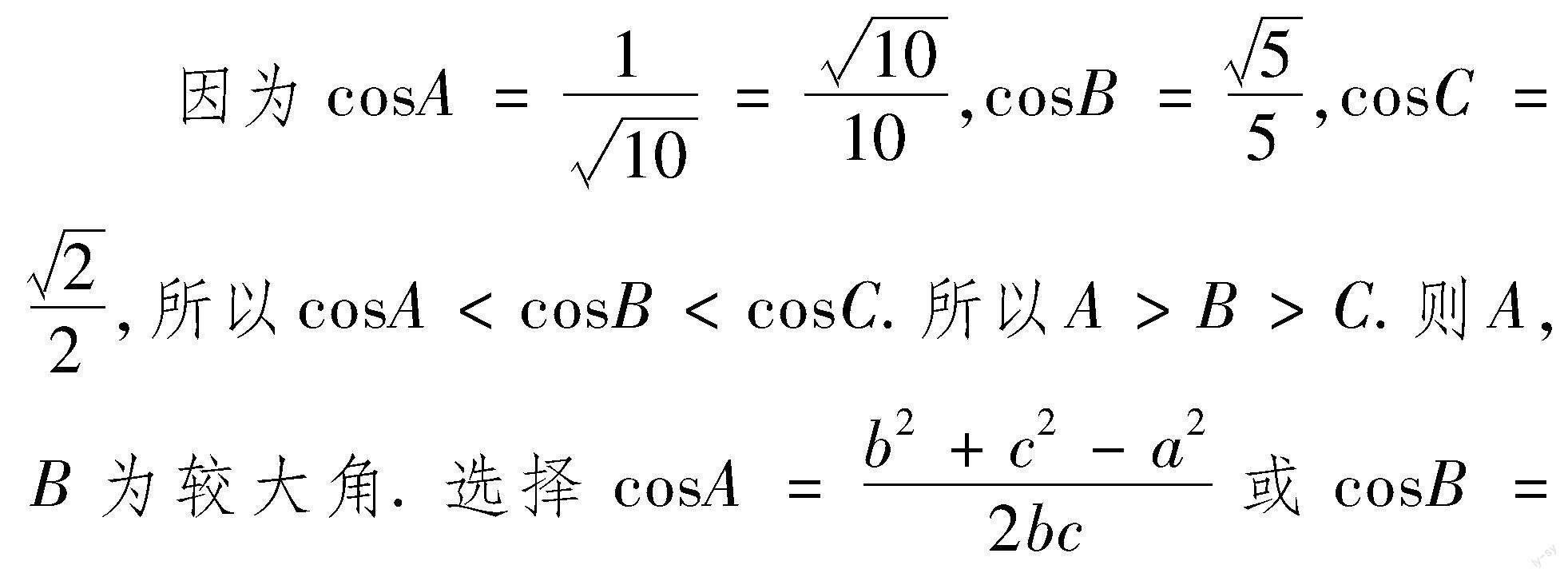

在解三角形问题中,根据条件建立方程计算线段长度或角度时经常会产生“增解”问题.本文笔者以2023年全国新高考Ⅰ卷17为例,明晰“增解”来源,理清“舍根”方法,并提出避免產生“增解”的几种策略,希望对读者有所帮助.
1 问题起源
(2023年全国新高考Ⅰ卷17)已知在△ABC中,A+B=3C,2sin(A-C)=sinB.
(1)求sinA;(2)设AB=5,求AB边上的高.
分析:第(1)小题考查三角恒等变换求三角函数值,第(2)小题可通过等面积法求AB边上的高.即将问题转化为“三角形中,已知两个内角与一条边,求其他边长”.即求b.
可以发现,以上三种思路均采用余弦定理,思路2却产生了增解.原因在哪里?如何舍去增解?已知“两边一对角”情形下,选择哪个角使用余弦定理最佳?
2 为何有增解
2.1 “增解”的几何解释
2.2 “增解”的代数说明
已知a,c和角C,对角C使用余弦定理,并将其整理为关于b的一元二次方程b2-2abcosC+a2-c2=0(*).判别式Δ=(2acosC)2-4(a2-c2),化简得Δ=4(c2-a2sin2C)=4(c+asinC)(c-asinC),则
①若方程(*)有两个不等的正数解,则该三角形有两解;
②若方程(*)有一个正数解,则该三角形有一解;
③若方程(*)无解或只有负数解,则该三角形无解.
限于篇幅,仅证明①.
3 如何舍去增解
4 避免产生增解的策略
策略1 对较大角使用余弦定理
策略2 运用射影定理
策略3 运用正弦定理
sinB=sin(A+C)=sinAcosC+cosAsinC=
解三角问题中,只要甄别好条件,运用余弦定理来辨析三角形解的个数也是可行的.由此,可帮助学生面对此类试题时做好决策,做到胸有成竹,事半功倍!
猜你喜欢
中学生数理化·中考版(2022年9期)2022-10-25 03:48:50
中学生数理化·中考版(2021年9期)2021-11-20 06:17:34
中学生数理化(高中版.高二数学)(2020年11期)2020-12-14 07:36:32
中学生数理化(高中版.高考数学)(2020年10期)2020-10-27 03:04:28
河北理科教学研究(2020年1期)2020-07-24 08:14:28
中学生数理化·七年级数学人教版(2019年9期)2019-11-25 07:34:34
中学生数理化·中考版(2017年3期)2017-11-09 02:07:37
初中生世界·九年级(2017年9期)2017-10-13 02:18:28
智富时代(2017年4期)2017-04-27 02:13:48
中学生数理化·七年级数学人教版(2016年9期)2016-12-07 08:28:52

