用深度神经网络实现高精度纳米光子器件的光谱计算

邱维阳,何 成,郑根让,易巧玲

(中山职业技术学院,广东 中山528400)

0 引言

由精心设计的微纳结构组成的新型光学器件已成为一个极具活力且富有成果的研究领域,因为其具有操控光流到纳米尺度的能力[1],得益于先进的数值模拟、制造和表征技术,人们能够设计、制造并展示具有复杂几何形状和排列的介电与金属微观及纳米结构。例如,由亚波长结构组成的超材料和超表面被称为元原子(meta-atoms),可展现出超越自然材料的卓越特性。光线导向、全息术、成像、传感和极化控制等研究领域已报道了多种元器件,微纳结构研究的兴起为光学应用领域提供了巨大的技术突破。但随着结构的复杂度越来越高,设计过程变得越来越具有挑战性。传统的设计路径依赖于器件优化,即从一些特殊结构(依赖于设计师的经验)通过求解麦克斯韦方程和边界条件得到电磁响应,将计算结果与设计目标进行比较获取调整方向并进行相应调整,不断重复此过程,直到设计的器件符合设计需求。代表性方法包括伴随方法、水平集方法、遗传算法和粒子群算法等,这些研究方法需要进行数百甚至数千次的模拟,直到器件性能达到可接受的范围,但非常消耗计算资源,需要耗费大量的人力且结果严重依赖于研究者的经验,并随着器件变得越来越精巧,这种研究变得越发困难。

深度学习在近年得到了快速发展[2],是一种数据驱动方法,可从数据中学习并用以前学习到的经验解决问题。最近,越来越多的深度学习方法被引入到物理研究中[3]。本研究采用深度神经网络来预测纳米多层膜结构的光学响应。随机生成了一百万个纳米多层膜结构,利用传输矩阵法[4]计算了相应的光谱,使用生成的结构及其相应的光谱来训练深度神经网络,对训练的深度神经网络预测光谱进行了定性与定量分析。

1 材料与实验方法

研究材料是一系列由SiO2/Si3N4薄膜组成的夹层结构(如图1所示),将研究波段锁定在400～750 nm的可见光波段。为了更好地调制光波,将材料光学厚度限制在60～200 nm,结合SiO2、Si3N4的折射率(分别约为1.57和2.03)将SiO2和Si3N4材料厚度相应限制为40～130 nm和30～100 nm。

图1 纳米多层膜结构Fig.1 Nano multilayer film structure

其中紫色和绿色分别代表SiO2和Si3N4层。样品总厚度变化范围为350～1100 nm。

结合电磁波的连续性条件和边界条件,考虑法向入射情况,将传输矩阵表示为:

(1)

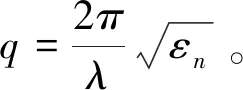
由于公式(1)表征了入射波和出射波之间的关系,因此很容易将公式(1)扩展到多层情况。对于一个通过n层材料的电磁波,会连续发生n次入射和相应的n次出射,传输矩阵表示如下[15]:

MnMn-1…M2M1

(2)

其中,Mi代表第i层的传输矩阵。根据矩阵的结合律,计算每个层的传输矩阵的累积乘积,得到一个单独的矩阵M。可以用4个变量,即m11、m12、m21和m22表示矩阵M中的4个元素,即:

(3)

对于TE模式,整体反射率和透射率可以写成:

(4)

(5)

其中,qi和qo分别表示入射波矢量和出射波矢量在法线方向上的投影,如果入射介质和出射介质都为空气,则有:

(6)

在可见光波段内,SiO2和Si3N4的介电函数接近于常数(对于SiO2,介电函数范围为1.4836～1.4698,对于Si3N4,介电函数范围为2.0978～2.0274),这里以其他研究者的计算结果为计算依据[16-17]。

随机生成一百万个不同的多层膜结构,利用传输矩阵法计算这些结构的光响应。由于透射率和反射率是互补的,因此只通过透射光谱来训练网络,这并不会损失一般性,但可节省时间和存储空间,生成的结构及其对应的光谱如图2所示。

图2 随机生成的结构及其由TMM计算得出的相应电磁响应Fig.2 Randomly generated structure and its corresponding electromagnetic response calculated by TMM

蓝色线表示透射率,橙色线表示反射率。每个光谱上方对应的是其材料结构。紫色和绿色分别代表SiO2和Si3N4层。

其中,n1=10(对应于10层膜的厚度),n2=n3=512,n4=n5=256,n6=n7=128,n8=71(对应于波谱的采样波长数,每个波长间隔为5 nm,从400～750 nm)。

搭建的网络是一个8层神经网络,图3为网络示意图。输入层包含10个神经元,与设计的10层膜材料结构相匹配(因此有10个参数)。每5 nm采样一次光响应,因此从400～750 nm采样了71个波长。相应地,网络的最后一层包含71个神经元,与光谱匹配。除了第一层和最后一层,还有6个隐藏层在输入层和输出层之间,称为神经网络中的隐藏层。第1、3、5个隐藏层是全连接层,每个全连接层的神经元与前一层中的所有神经元相连。第2、4、6个隐藏层是激活层。设置激活层的原因是为了引入非线性特性,增加神经网络的容量[18]。使用LeakyReLU作为激活函数,LeakyReLU是经过修改的线性整流单元(ReLU)[19],图4是ReLU和LeakyReLU的示意图,它们在输入为正时输出相同,而在输入为负时输出不同。在输入为负时,LeakyReLU中的微小斜率是为了避免神经元死亡(在ReLU中如果神经元输入为负,它的梯度和值都为零。如果大量神经元输入为负,它们可能无法再次被激活,导致模型无法被正常训练)。

图3 构建的网络Fig.3 Constructed network

图4 ReLU和LeakyReLUFig.4 ReLU and LeakyReLU

可以看到,当输入为正数时,在两种情况下输出等于输入本身,但当输入为负数时,ReLU的输出为零,而LeakyReLU的输出为输入的1%,呈现出微小的斜率。

搭建好的深度神经网络的初始参数是随机的,并不能很好地预测光谱,因此需要对参数进行优化,即对模型进行训练。为了明确优化方向,需要定义一个表征神经网络输出(预测值)与实际值之间的差异损失函数[20],而所有样本的平均损失构成了代价函数,其为训练神经网络时的一个关键指标。训练目标是最小化代价函数,令预测结果更接近实际值。使用均方误差作为损失函数,因为它在处理回归问题时是一个很好的指标,能够表征预测光谱与实际值之间的偏差。

选择好损失函数后开始优化网络参数,使代价函数尽量小。但由于在深度神经网络中通常有数百万个参数(此案例中约为17万个),对于这样大规模的参数,合适的优化方法是影响最终结果的重要因素。在一些简单情况下,如单变量函数优化,牛顿迭代法是一种很好的求数值解的方法。但当变量扩展到多变量(在深度学习中,数百万非常常见)时,由于必须导出海森矩阵[21],其参数高达万亿量级,使得此方法变得难以应用。而实际上,计算包含数万亿个参数这样巨大的矩阵几乎是不可能的。优化这样大规模参数的实际方法是使用梯度下降或更高效地使用随机梯度下降(Stochastic Gradient Descent)[18]。相关研究表明,使用传统的随机梯度下降时可能会出现收敛缓慢甚至陷入局部最小值的情况,因此提出了改进方法,如 AdaGrad、RMSProp、Adam、AdamW、RAdam[10],故选择Adam作为优化方法。

在实验中设置了5000个轮次来训练深度神经网络,经过若干次尝试,将学习率设置为0.0001,且每200个轮次训练完成后将学习率降低20%,使得代价函数更容易接近其极小值,从而获得更好的模型性能。

2 结果与分析

将样本分为两部分:一部分是训练集,占总样本量的80%,用于训练网络。其余的20%组成验证集,用于验证模型是否确实学会了预测光谱(即不仅仅是记住了训练数据)[22]。为了提升训练效率,每个训练周期中都对训练集进行乱序操作,这样虽然训练集是固定的,但样本顺序在训练期间会不断变化,可以泛化模型并增强训练效果。

y轴刻度被设置为对数级别,以便更清晰展示。(a) 所有训练样本的训练过程。(b) 清洗后的数据集的训练过程(去除了峰谷数量之和大于3的结构)。

图5(a)和图5(b)之间存在两个主要差异:在清洗后的数据集中,训练阶段的代价函数值和验证阶段的代价函数值均比完整的数据集低,因为光谱被简化,网络可以更好地描述它们。②训练阶段的代价函数和验证阶段的代价函数存在偏差,这意味着在清洗后的数据集中出现了过拟合。因为清洗后的数据集中的样本大小只有完整数据集的22%,网络学到了一部分训练集样本特有的特征。

图5 训练过程中代价函数的演化过程Fig.5 Evolution of cost function in training process

所有的损失函数的平均值为网络的代价函数,它表征了神经网络的预测结果与真实值之间的均方误差。

从图5可以看到,代价函数在开始的前1000个轮次时迅速下降,在1000～2000轮次下降速度明显放缓,最后3000个轮次对代价函数的绝对改善已经非常小。这一曲线与其他深度学习训练过程相似,由于网络的初始参数是随机生成的,因此一开始无法很好地预测光谱,导致代价函数非常大。在优化过程中,将梯度进行反向传播来得到代价函数对每个参数的导数,优化器(Adam优化器)根据梯度对参数进行一定的调整。随着训练的进行,网络中的参数被优化器逐步调优,网络可以越来越精确地预测谱图。图6是随着训练的进行光谱的预测效果变化。

图6 光谱的预测效果变化Fig.6 The change in effectiveness of spectra prediction

橙色线是真实值,蓝色线是预测结果。随着训练过程的进行,这两条线逐渐靠近,意味着深度学习模型已经学会了如何通过结构来预测光谱。

训练过程完成后,可以使用这个经过训练的深度神经网络来计算给定结构的光谱。图7显示了一些随机生成的结构及其由TMM和深度神经网络计算出的相应光谱。虽然深度神经网络在大多数的结构上表现得非常好,但仍发现它在光谱结构较复杂的结构上表现略差。这种现象主要是因为光谱结构的复杂程度超过了深度神经网络的表达能力[18],导致欠拟合。解决这个问题的直接方法是增加网络容量,如加深和加宽网络,但会带来计算负担。

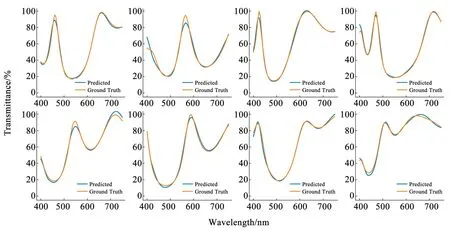
图7 随机生成的结构和相应的光谱Fig.7 Randomly generated structures and corresponding spectra

图7中上面4个图是对训练集中样本进行预测的结果,下面4个图是对验证集中样本进行预测的结果,两者均表现出出色的预测能力。蓝色线是预测结果,橙色线是真实值。

在构建更复杂的网络前分析了数据分布情况,以了解模型在整个数据集上的表现,结果如图8。从图8(a)和图8(b)中可以看到,超过94%的样本偏差小于2.5%,超过99.7%的样本偏差小于5%。对于如此少的情况(只有不到0.3%的样本偏差大于5%),进一步复杂化模型并不值得(不但带来计算负担,还可能造成过拟合)。但为了关注偏差较大的样本,提取了这些样本并绘制预测光谱,将其与基准光谱进行比较,光谱图如图8(c)和图8(d)中。由此可知,无法很好预测的光谱具有3个峰值和3个谷值,总共有6个极值点。

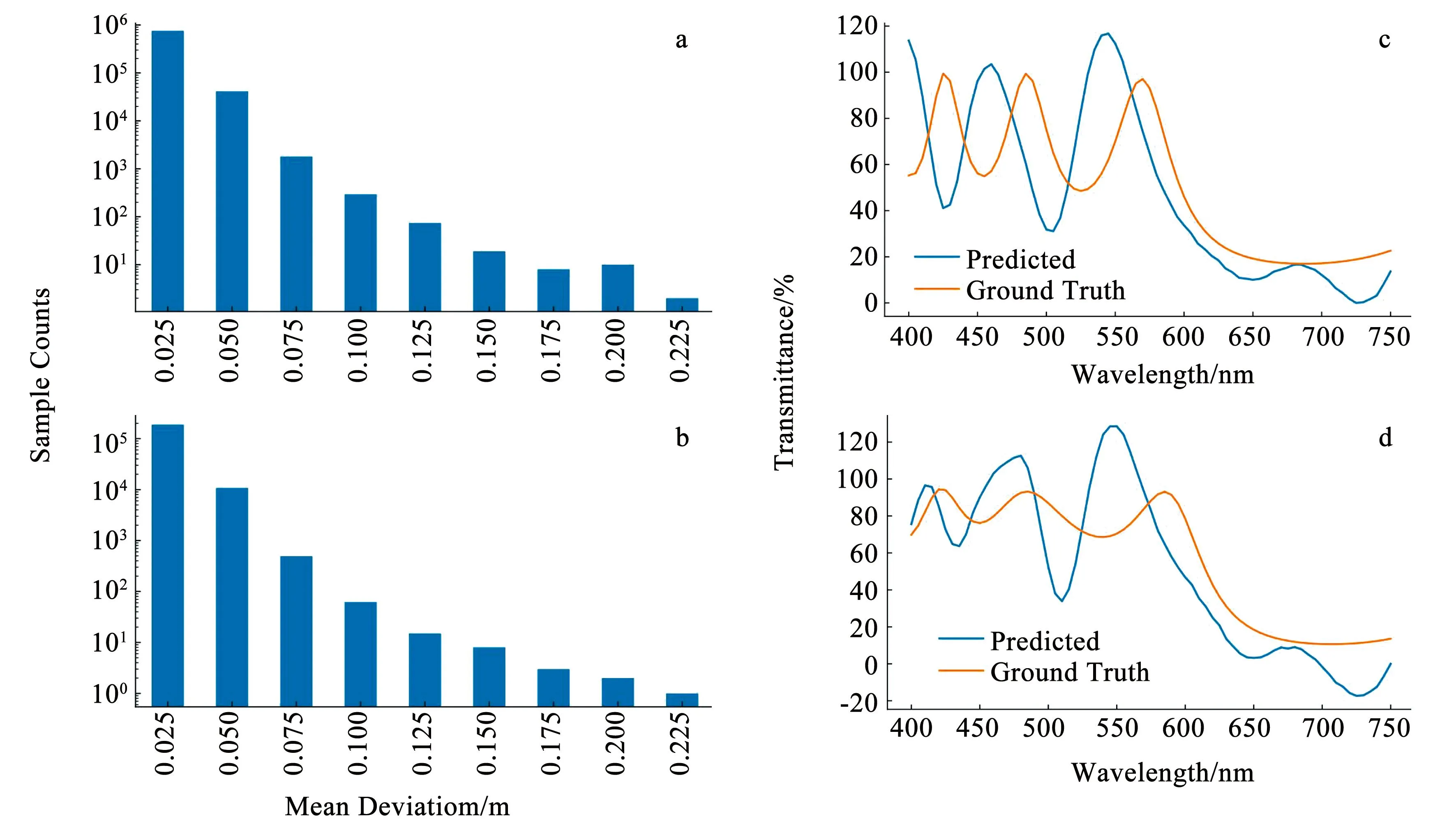
图8 数据分布情况Fig.8 Data distribution

图8(a)和图8(b)分别显示了训练集样本和验证集样本的预测光谱与真实光谱的平均偏差,y轴为对数刻度以便清晰展示。图8(c)和图8(d)分别显示了训练集和验证集中最差结果的情况。

实际上,一个实用的光学器件通常只关注一个或两个特定的波长,并在这些特定的波段提供高透射或高反射。因此在实践中,具有大量透射峰或反射峰的光学器件并不常见。从这个角度来清洗训练数据,剔除具有超过3个极值的样本。这意味着用于训练模型的数据最多只能具有2个峰值和1个谷值或1个峰值和2个谷值。在清洗数据集后重新训练模型。图9为随机选择的结构光谱预测结果与真实结果的比较。从视觉上可以轻易发现模型的预测能力有了显著提高。

图9 透射峰谷数量之和不超过3的光谱Fig.9 Spectrum in which the sum of transmission peaks and valleys does not exceed 3

图9上面4个图是从训练集中预测的结构,下面4个图是从验证集中预测的结构,它们都是随机选择的。蓝色线是预测结果,橙色线是真实值。

量化分析见表1。前2000个轮次的训练过程表现出了显著的预测能力提升,在训练2000个轮次之后,完整数据集和清洗后的数据集的代价函数下降非常缓慢,但仍分别获得了约25%和23%的改进(只考虑验证集以进行更有效的评估)。研究人员可根据需求决定这种精细化程度是否值得(参见图6中的预测变化)。

表1 量化分析结果

代价随着训练过程逐渐下降,使用完整数据集的代价对比清洗后的数据集代价(去除极值数量超过3个的光谱)。为方便展示,数字被放大了10 000倍。

随着训练过程的进行,完整数据集的代价函数值从7.9906(初始随机参数)降至0.0004737;清洗后的数据集的代价函数值从5.6119(初始随机参数)降至0.0001689。由于代价函数是所有样本上损失函数的平均值,而实验中使用的损失函数是均方误差损失,即所有样本的预测结果与真实结果之间偏差的平方平均值。对其开方后得到完整数据集的均方根误差仅为2.2%,清洗后的数据集的均方根误差仅为1.3%,这显示了相当高的预测精度。

3 结论

开发了一种数据驱动方法来高效预测纳米多层膜结构的光谱,该方法可以在不到20 μs的时间内(CPU为i3-6100)预测实际结构的光谱,均方根误差仅为2%。与传统设计方法相比,这种超高速和高精度的预测方式具有较大的优势,开创了一种新的研究范式。与其他深度学习应用一样,虽然此模型需要事先进行训练,但这只是一次性成本,且模型参数只需占用不到1 MB的空间,易于复制和广泛使用。