鱼眼型高速连接器的材料性能识别与压接特性仿真研究*
侯冰玉,盛依航,耿秀侠,胡俊,王剑,王世堉,王明智
(1.西安电子科技大学机电工程学院,西安 710071;2.中兴通讯股份有限公司,广东深圳 518000)
0 引言
电连接器通常被用于连接电力系统中2 个器件或设备。随着电子、通信等行业中的器件和系统朝微型化方向发展,多芯片封装、功率转换与发电、微机电系统(MEMS)器件、太阳能、LED 以及汽车接口技术等应用领域对连接器性能的要求日益提高[1-3],普通的焊接式连接器已经无法满足设计需求。将完成贴装后的元器件焊接于PCB 上,再将其与插座进行压接配合,压接时需要避免元器件、连接器插针等变形或损坏,因此装配难度较高[4]。焊接式连接器的抗振性较差,返修难度大[5]。压接配合是实现过盈配合零件连接的传统装配方法之一,该方法有助于提升连接的可靠性和经济性。该方法不存在与焊接工艺相关的问题,此外,压接配合还具有过程简便、组装灵活、方便现场维修和更换等优点[6-8]。鱼眼型高速连接器作为1 种可移动连接装置,其利用弹性可变形顺应针与PCB 孔实现过盈配合,从而建立良好的机械连接和电气接触[9-10],可用于实现不同系统间的电能和电信号的传输。连接器的工作性能无法被直接量化,通常选用插拔力这一指标作为评估其性能的主要参数[11-14]。因此,研究顺应针的几何参数与插拔力的关系尤为重要。在对电连接器进行插拔时,插针在发生弹性变形的同时需要克服摩擦力,因此插入力往往大于拔出力。为确保连接器使用的顺畅性和稳定性,插入力不宜过大,同时拔出力也不宜过小[15-16]。
1 实验原理
采用有限元仿真技术模拟顺应针插入PCB 孔的过程,得到载荷-位移曲线。由于受到连接器本身尺寸、局部空间等因素限制,采用常规实验方法获取连接器关键部位材料的力学性能参数比较困难。纳米压痕技术是1 种材料参数测试方法,使用刚性压头在被测样品表面施加压力,得到压痕的载荷-位移曲线,经过对实验数据的深入剖析,利用相关公式进行精确计算,并结合有限元仿真与算法识别技术,获取样品材料的物性参数[17-18]。纳米压痕技术可以实现对材料局部力学性能的无损检测,样品制备过程简便,从而为高速连接器关键部位材料性能的精准测试提供了可行性。
鱼眼型高速连接器实物与PCB、顺应针形貌如图1 所示。将顺应针插入PCB 孔,顺应针的2 个梁结构与孔内壁接触。由于顺应针与PCB 孔间存在过盈配合,顺应针的梁结构受到力的作用向内侧发生形变,该形变会在孔内壁与鱼眼结构间产生足够的正向接触压力,从而确保鱼眼结构在变形后能与PCB 保持可靠的接触,该方法可实现连接器与PCB 的可插拔免焊连接[19]。采用纳米压痕实验与内点罚函数优化算法相结合的方法,通过反演求解得到鱼眼型高速连接器顺应针和PCB 孔镀层的材料性能参数,并建立了用于鱼眼型高速连接器插拔特性分析的有限元模型。通过参数化建模,分析了顺应针和PCB 孔的几何参数对插拔力的影响。

图1 鱼眼型高速连接器实物与PCB、顺应针形貌
2 基于纳米压痕实验的材料参数识别
2.1 纳米压痕实验
实验在室温下进行,首先对样品进行切割、磨样、抛光及镶样处理,使用纳米压痕仪(安捷伦Nano Indenter G200)进行纳米压痕实验。将顺应针的最大加载载荷设置为80 mN,将PCB 孔镀层的最大加载位移设置为1 000 nm,使用顶角为115°的金刚石Berkovich压头进行纳米压痕实验,确保每次实验都能实现100%卸载。顺应针和PCB 孔镀层的压痕如图2 所示,纳米压痕实验的载荷-位移曲线如图3 所示。该曲线可以分为加载和卸载2 个部分,分别对应塑性加载和纯弹性卸载2 个阶段。加载部分一般用于分析材料的硬度、屈服应力及应变硬化指数等塑性性能,而卸载部分则多用于分析材料的弹性模量[20]。

图2 顺应针和PCB 孔镀层的压痕
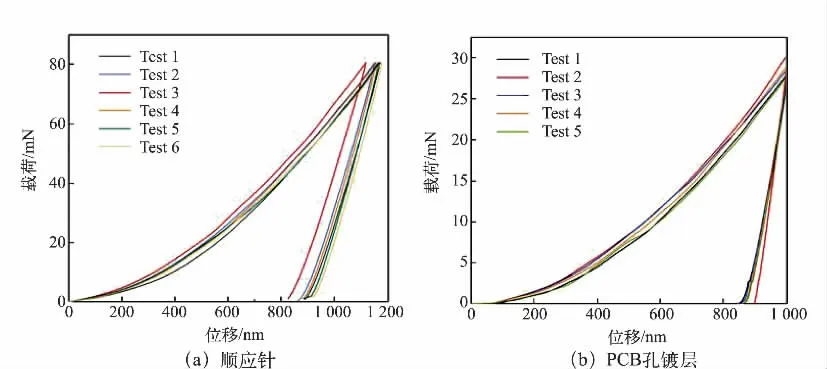
图3 纳米压痕实验的载荷-位移曲线
2.2 参数识别技术建模
依据纳米压痕实验的载荷-位移曲线得到顺应针和PCB 孔镀层的力学性能参数,并结合参数识别技术与优化算法进行计算。建立纳米压痕实验的有限元模型,并假定材料为各向同性。由于泊松比对纳米压痕实验的载荷-位移曲线并无明显影响[21],因此将泊松比设置为0.3。需要合理规划材料参数的设计空间,并根据设计表中的材料物性参数进行压痕仿真,从而得到压痕变形-载荷曲线数据库。
采用Hollomon 硬化法描述材料的应力应变曲线,Hollomon 硬化法的表达式为
其中,σ 为拉伸应力,E 为弹性模量,ε 为拉伸应变,εy为屈服应变,σy为屈服应力,n 为应变硬化指数。
目标函数可以用来量化压痕仿真曲线与压痕实验曲线之间的残差。基于实验获得的载荷-位移曲线设计目标函数,采用优化算法确定被测材料的力学性能参数。目标函数g(c*)为
其中,c*是1 个列向量,包含材料的σy和n,即c*=(σy,n)T。himpt(c*)为通过仿真获取的纳米压痕过程中的瞬时快照值,hexp为通过实验获取的纳米压痕过程中的瞬时快照值,Pmax为最大加载载荷,P0为初始加载载荷。
g(c*)可以反映残差与材料设计变量的关系。依据材料参数设计空间进行有限元仿真,可得到目标函数与材料设计变量之间关系的离散值。采用二元三次多项式对上述关系式进行拟合。二元三次多项式包含10个拟合系数。通过最小二乘法对二元三次多项式进行拟合,得到了目标拟合函数 g(x,y)的拟合系数 bk(0≤k≤9)。
其中,x 表示σy,y 表示n。
采用内点罚函数优化算法对式(2)进行求解。该算法可以通过连续计算目标函数及其梯度信息,在迭代过程中自动更新参数值。该算法在MATLAB 优化工具中可用。初始迭代点应该位于先前定义的边界约束内。当目标函数的变化量小于1×10-6时,则算法的迭代过程满足收敛准则。在此基础上,采用内点罚函数算法调整2 个设计变量σy和n,确保g(x,y)达到最小值,最终得到顺应针和孔镀层的材料参数。参数识别流程如图4 所示。

图4 参数识别流程
2.3 物性参数识别结果
微纳米压痕测试技术是基于载荷-位移曲线建立相应的数学模型,进而得到材料力学性能参数的方法。最常见的计算材料弹性模量的方法是Oliver-Pharr模型[22],该模型的表达式为
其中,Er为折减模量,Ei为压头的弹性模量,S 为卸载刚度,β 为与压头几何形状相关的常数,v 为被测材料的泊松比,vi为压头的泊松比,hc为接触深度,A为接触面积,Fmax为最大法向载荷,hmax为最大压入深度。
将通过压痕实验得到的数据带入式(4)~(7)进行计算,顺应针的弹性模量为68.203 GPa,PCB 孔镀层的弹性模量为62.061 GPa。依据压痕实验载荷-位移曲线及反演求解方法识别塑性参数。顺应针、孔镀层的σy与n 迭代识别结果如图5 所示。顺应针的塑性参数被设定为850 MPa≤σy≤1 200 MPa,0.01≤n≤0.22,顺应针σy的取样间隔为50 MPa,顺应针n 的取样间隔为0.05;孔镀层的塑性参数被设定为240 MPa≤σy≤380 MPa,0.02≤n≤0.08,孔镀层σy的取样间隔为20 MPa,孔镀层n 的取样间隔为0.01。

图5 顺应针、孔镀层的σy 与n 迭代识别结果
基于Hollomon 硬化法开展锥形压痕有限元仿真,建立用于多项式拟合训练的压痕载荷-位移曲线数据库,依照参数识别流程,采用迭代收敛的方法得到顺应针、孔镀层的σy分别为972.19 MPa、314.02 MPa,顺应针、孔镀层的n 分别为0.189、0.053。顺应针、孔镀层的参数识别结果如表1 所示。纳米压痕的仿真结果与实验结果对比如图6 所示,曲线呈现出高度的一致性。

表1 顺应针、孔镀层的参数识别结果
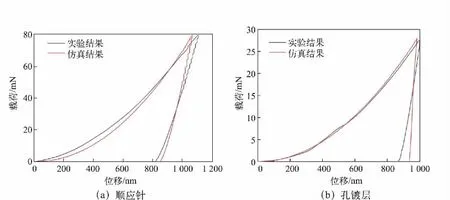
图6 纳米压痕的仿真结果与实验结果对比
3 插拔仿真与实验
3.1 仿真建模
鱼眼型高速连接器的顺应针和PCB 孔的压接配合属于弹塑性接触问题。在接触过程中产生的接触压力、插入力和弹塑性变形都属于静态分析的范畴[23]。因此,使用Abaqus 仿真软件对其插拔过程进行有限元模拟,采用表1 的参数。当顺应针和PCB 孔进行装配时,孔镀层会产生一定的形变。为了更准确地模拟插拔力的变化,在建立仿真模型时,将顺应针、PCB 孔、孔镀层作为3 个独立的模型进行仿真,如图7 所示[24]。
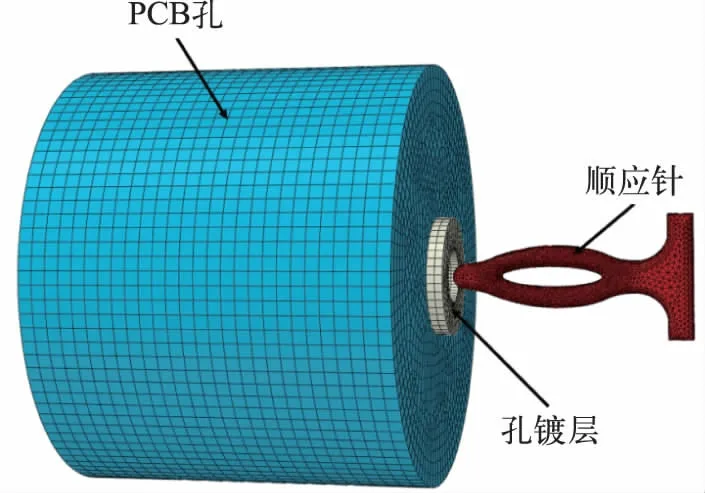
图7 仿真模型
在顺应针和PCB 孔的有限元分析模型中,顺应针采用六面体网格,PCB 孔采用四面体网格,并采用了线性几何阶次来描述网格单元。减小接触区域的网格尺寸,增大远离接触区域的网格尺寸,通过这样的划分策略可以缩短有限元模拟过程的计算时间并提高计算准确性。设置插入和拔出步骤,选择通用接触作为相互作用方式,将PCB 孔与孔镀层模型设定为绑定约束,将顺应针与孔镀层的摩擦模型设置为“罚摩擦”,通过控制顺应针的移动进行过程仿真。
鱼眼型高速连接器的插拔仿真过程如图8 所示,顺应针与PCB 孔开始接触时的形貌如图8(a)所示。当插入力达到峰值时,顺应针与PCB 孔的相对位置如图8(b)所示,此时插入力为3.638 N。完全插入后的顺应针与PCB 孔的相对位置如图8(c)所示,随后将顺应针拔出,插拔力由3.186 N 迅速减小至2.687 N,再迅速增大至拔出力峰值,即2.727 N。完全拔出后的顺应针如图8(d)所示。

图8 鱼眼型高速连接器的插拔仿真过程
3.2 实验过程
使用电动拉压力实验机ZQ-990B 进行鱼眼型高速连接器的插拔实验,在X、Y 轴二维平台、双向拉压夹具与高速相机的辅助下,将顺应针和PCB 孔固定,在上位机中设置了插入与拔出步骤,在对单个顺应针进行初次的插入-拔出测试后,整理实验数据得到载荷-位移曲线,并对实验数据进行分析。
3.3 实验与仿真结果对比
通过实验得到的最大插入力为3.833 N、拔出力为2.419 N;通过仿真得到的最大插入力为3.638 N、拔出力为2.727 N。插入力的误差为5.027%、拔出力的误差为12.732%。插拔力的实验曲线和仿真曲线对比如图9所示,曲线呈现出较高的一致性,说明仿真结果可以准确地反映最大插入力。在实验过程中,实验机产生的振动可能导致实验曲线所显示的插拔力数值出现波动[25]。

图9 插拔力的实验曲线和仿真曲线对比
4 关键几何参数对插拔力的影响
顺应针与PCB 孔镀层的几何参数如图10 所示。为了研究关键几何参数对插拔力的影响[26],使用Abaqus 有限元软件进行仿真,得到插拔仿真过程的载荷-位移曲线并对插拔力数据进行分析。结果表明,孔镀层厚度Dh、外椭圆长轴Wa对插拔力的影响可以忽略,外椭圆短轴Wb、顺应针厚度H 与插拔力大小成正比,孔镀层内半径Dr、圆角R、中心距L、内椭圆长轴Na及内椭圆短轴Nb与插拔力大小成反比。

图10 顺应针与PCB 孔镀层的几何参数
在鱼眼型高速连接器的设计中,为了使顺应针在插入过程中不发生明显的变形与磨损,要减小插入力;同时,为了使顺应针与PCB 孔形成紧密且可靠的连接,应增大拔出力,即压接力,以确保接触件之间接触稳定、抗振动性能好、接触电阻小[27],从而避免其在外界振动冲击的影响下发生脱离现象。对通过插拔力仿真得到的载荷-位移曲线进行深入分析,Dr、Wa、L 与插拔力的增减效率呈现出不同的关联,为了实现在减小插入力的同时提高拔出力,应该对上述3 个参数进行调整。
调整不同几何参数后的插拔力曲线如图11 所示。由图11(a)可知,当Dr由0.144 mm 增加至0.164 mm时,插入力由6.351 N 减小至3.654 N,下降了42.47%;拔出力由4.214 N 减小至2.996 N,下降了28.90%。插入力的下降速率更快。由图11(b)可知,当Wa由0.405 mm 增加至0.445 mm 时,插入力由4.747 N 增大至4.933 N,提高了3.92%;拔出力由3.498 N 增大至3.825 N,提高了9.35%。拔出力的提高速率更快。由图11(c)可知,当L 由0.007 mm 增加至0.037 mm 时,插入力由5.234 N 减小至4.767 N,下降了8.92%;拔出力由3.508 N 增大至3.954 N,提升了12.71%。需要注意的是,当L 由0.037 mm 增加至0.047 mm 时,插入力没有继续下降,而是由4.767 N 提高至4.924 N。

图11 调整不同几何参数后的插拔力曲线
5 结论
本文采用纳米压痕实验及卸载刚度分析,测得顺应针和孔镀层的材料弹性模量。采用多项式函数拟合目标函数,通过反演求解的方法对塑性参数进行识别,从而确定了顺应针、孔镀层的屈服应力和应变硬化指数。将识别到的参数输入Abaqus 仿真软件中,模拟顺应针的插拔过程。对比通过仿真与实验得到的载荷-位移曲线,插入力的误差为5.027%、拔出力的误差为12.732%,这一结果验证了利用仿真研究顺应针和PCB 孔的几何参数对插拔力影响的可行性。最后,调整顺应针与孔镀层的关键几何参数并进行插拔仿真得到插拔力载荷-位移曲线。结果表明,调整孔镀层内半径、外椭圆长轴以及中心距这3 个参数,可以有效降低顺应针的插入力,同时提高其拔出力。本文的研究结果为鱼眼型高速连接器物性参数的识别和压接可靠性的优化提供了参考。

