恒频声学二极管的设计及特性研究*
王颖 郭翔鹰† 杨晓东
(1. 北京工业大学 材料与制造学部,北京 100124)
(2. 机械结构非线性振动与强度北京市重点实验室,北京 100124)
引言
二极管是一种单向非互易的能量传输途径,在电子学中发挥着关键作用[1,2].近年来,该概念已扩展到热传导和弹性波操纵[3].
声二极管是一种允许声波或弹性波沿一个方向移动而反方向不通过的装置.这种单向声流可以消除声波同时向两个方向传播并相互干扰所引起的声干扰,从而提供更明亮、清晰的超声波图像.由于这种单向声流可以提供更明亮、清晰的超声波图像,它为设计师在声子晶体的制造和材料检测[4,5]中的应用提供了新的灵感.
目前,实现声波非互易性的方法被广泛研究[6-8].Liang于2009年提出了声二极管的第一个理论模型[9],但是此模型是基于线性结构的声二极管,遵循线性系统的互易原理[10],在严格意义上不被认定为二极管.学者们研究证明非线性可以通过两种方式提供稳定的二极管效应:谐波产生和分岔[11-14].在由一段非线性介质和线性声子晶体组成的声学二极管中,非线性介质中产生高次谐波[15],声子晶体的带隙导致总能量的不对称传递[11,16].但是这种声二极管会导致输出与输入信号相比发生频率变化,从而导致信号丢失以及正向传输率较低.
大部分基于非线性效应的声二极管都改变了频率.目前面临的问题是如何利用非线性效应,在不改变入射波方向和频率的情况下实现声波整流.在本文中提出了一种不同的理论模型,该模型的显著特点是在不改变入射波频率的情况下实现单向能量传输.
1 单原子声二极管
1.1 理论模型
如图1所示设计单原子声二极管,其理论模型由两部分组成:右侧弱非线性弹簧质量链和左侧变截面杆.由于结构的不对称性,当在结构的左右两端施加相同的激励时,入射到非线性弹簧质量链的振幅变得不同.而弱非线性声子晶体的色散关系会受到入射振幅的影响,振幅增大到一定值频率处于通带范围,否则处于带隙范围.因此,如果激励具有适当的频率和幅值,就可以通过结构的不对称性改变声子晶体正反方向受到的激励幅值,使非线性声子晶体正反向传输的带隙范围不同,从而实现不对称传递,实现弹性波的单向传输.下面的分析将给出详细的理论结果.

图1 单原子声二极管理论模型Fig.1 Theoretical model of a single-atom acoustic diode
1.2 非线性弹簧质量链
模型中的弹簧质量链由质量为m的质量块和非线性软弹簧周期性排列组成,其中弹簧具有式(1)所示的非线性力-位移关系:
F=kx+Γx3
(1)
其中Γ为负值.采用摄动方法[17]来求解非线性方程,引入扰动参数ε到式(1)可得:
F=kx+εΓx3
(2)
(3)


(4a)
(4b)
在弱非线性链中,只需要考虑ε0和ε1项,代入方程(3)得到ε0和ε1的独立方程分别为:
(5a)
(5b)
可以发现,式(5a)是与线性弹簧-质量链周期系统相同的,由布洛赫定理可得:
(6)
式(6)代入式(5a)可得:
(7)
(8)
将式(7)、式(8)代入式(4b)可得到非线性弹簧-质量链周期系统的色散方程:
(9)
得到非线性周期链中带隙形成的频率随着入射振幅增加而减小,图2为不同入射振幅下的波色散曲线.

图2 不同振幅的色散曲线Fig.2 Dispersion curves for the different amplitudes
1.3 变幅杆


图3 圆锥型变幅杆Fig.3 Conical variable amplitude rod
杆的物理参数包括:密度ρ、弹性模量E和圆频率ω,则可得到变幅杆的动力学方程如下:
(10)
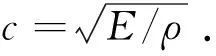
(11)
频率方程:
(12)
其中,N为杆两端的直径比,N=D1/D2.
锥形变幅杆的长度L通过式(13)得到:
(13)
其放大因子为
(14)
式(14)得出了设计不同振幅放大率的变幅杆的方法,以非线性周期链带隙的起始频率作为入射频率,并根据所需的入射频率设计直径比N,再由式(13)对变振幅杆长度L进行设计.因此,当激励具有适当的频率和振幅时,就可以实现弹性波的单向传输.下面通过有限元仿真验证理论计算.
1.4 仿真结果
基于式(9)对模型进行参数设计,选择以下参数,求得弹簧质量链的带隙范围.
m=2kg,k=2*106N/m,r=3cm,h=9cm.
由于4~8cm的入射振幅对设计模型的带隙起始频率有显著影响(如图4所示),因此在接下来的仿真中选择4cm和8cm作为带隙起始频率.即正向传输通过弹簧质量链的入射振幅为4cm,反向传输通过弹簧质量链的入射振幅8cm.根据求得的带隙范围对模型进行瞬态仿真,使用Ansys软件测量正反向传输的第一个和第九个质量块的位移,多组频率仿真发现系统上设置1840 rad/s的正弦激励效果最好.

图4 振幅对带隙起始频率的影响Fig.4 Effect of the amplitude on the onset frequency of the band gap
通过公式计算得到变幅杆的参数如下:
m=2kg,ρ=7850kg/m3,
D1=4cm,D2=2cm,L=8.7cm.
声学二极管模型的正反向传输如图5所示,灰线和红线分别是第一质量和第九质量的位移.发现图5(a)中的正向传输速率约为28%,而图5(b)中的反向传输率很低,仅有5%.引入对比度f如下:
(15)

(a)正向传输
可以看出对比度的范围为f∈[0,1],对比度趋于1时,整流效果最佳.由式(15)以及图5中的数据可求得对比度为0.7,达到了声学二极管模型的非互易性.这是由于变幅杆放大了振幅,改变了反向传输的色散关系,导致反向传输时频率处于非线性弹簧质量块的带隙频率范围内.
2 双原子声二极管
2.1 理论模型
单原子声二极管的带隙起始频率较高,应用范围较窄,因此进行双原子声二极管的研究.双原子声二极管理论模型如图6所示.

图6 双原子声二极管理论模型Fig.6 Theoretical model of a two-atom acoustic diode
2.2 非线性弹簧质量链
右端的弹簧质量链由质量m、M和非线性弹簧周期性排列组成.和1.2节的单原子弹簧质量链一样,可由牛顿第二定律写出运动方程:
u2n-1)3+εΓ(u2n-u2n+1)3=0
(16a)
u2n)3+εΓ(u2n+1-u2n+2)3=0
(16b)
由布洛赫定理,设线性部分的解为:
u2n=Acos[κd(2n)-ωt]
(17a)
u2n+1=Bcos[κd(2n+1)-ωt]
(17b)
则可求得线性部分色散关系:
(18)
(19)
从而可求得
η2cos2kd]
(20)
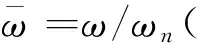
绘制如图7所示的色散曲线,发现和非线性单原子周期链一样,非线性双原子周期链带隙的起始和终止频率随着入射振幅的增加而减小.

图7 双原子模型的色散曲线Fig.7 Dispersion curve of diatomic model
2.3 仿真结果
变幅杆在本模型和上面单原子声二极管模型中起到的作用是完全一样的,其理论推导见1.3节.进行仿真模拟的步骤是和1.4节一样的,在此不做赘述.选择以下参数:
ρ=7850kg/m3,d=25cm,
M=2kg,R=3cm,H=9cm,
m=1kg,r=2.5cm,h=6.5cm.
通过计算发现此模型4cm~8cm的入射振幅带隙起始频率有显著影响,因此在接下来的仿真中选择4cm和8cm作为带隙起始频率.即正向传输通过弹簧质量链的入射振幅为4cm,反向传输通过弹簧质量链的入射振幅为8cm.使用多组频率仿真后发现系统设置频率为1260 rad/s的正弦激励效果最好.通过公式计算变幅杆的参数如下:
m=2kg,ρ=7850kg/m3,
D1=4cm,D2=2cm,L=8.7cm.
得到声学二极管模型正反向传输如图8所示.可以看出,图8(a)中的正向传输速率约为17%,而图8(b)中的反向传输率很低,仅有4%.由式(15)以及图8中的数据可求得对比度为0.62,双原子模型也达到了声学二极管模型的非互易性.
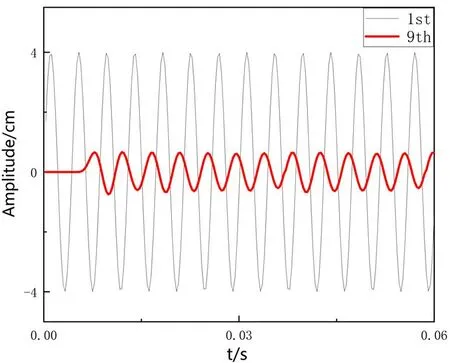
(a)正向传输
3 结论
本文建立了两种声学二极管的动力学模型,通过理论和数值研究了两种模型在不同外激励参数下的正反向传输特性.主要结论如下:
(1) 两种模型都能实现弹性波不变频的单向传输,并且具有与电子二极管相同的正向和反向特性.
(2) 非线性单原子模型色散关系受到入射振幅的影响较大,正向传输率较高.但带隙起始频率高,声学二极管的应用范围窄.
(3) 非线性双原子模型的工作频率较低,但入射振幅对其色散关系的影响较小,导致能够达到正向传输通过反向传输被抑制的频段很窄,故难以选取适当工作频率且适当工作频率的正向传输率也较低.

