卫星磁姿态控制方法与算法综述*

穆硕 占英 宝音贺西

(1. 清华大学 航天航空学院, 北京 100084)

(2. 内蒙古大学 电子信息工程学院, 呼和浩特 010021)

引言

自探索太空之初,磁姿态控制系统便因其轻便,可靠等诸多优点受到卫星设计者的青睐.第一颗成功使用磁姿态控制系统的卫星是Transit 1B,由美国约翰霍普金斯大学应用物理实验室(APL)设计.该卫星于1960年4月发射,采用被动磁控,进行了89天在轨操作[1].1960年11月,第一颗采用主动磁姿态控制的卫星Tiros II成功发射[2].

相比于其他控制方式,磁姿态控制系统具有质量轻、体积小、成本低、可靠性高,使用寿命长等诸多优点,是低轨近地卫星尤其是微小卫星实现稳定控制的首选.磁姿态控制系统依靠卫星自身磁矩m与地磁场强度矢量B相互作用,产生控制力矩T.被动磁控卫星主要通过永磁体与磁滞棒产生磁矩;主动磁控卫星则需要通过电流驱动磁力矩器产生所需磁矩.磁控力矩计算公式为:

T=m×B

(1)

从公式(1)中可看出,磁姿态控制系统的主要缺点是无法施加独立的三轴控制力矩,在每一瞬时只能产生垂直于卫星所处地磁场的控制力矩,这会大幅降低姿态控制效果,甚至出现瞬时不可控.

磁姿态控制卫星的可控性一直困扰着学者们.直到2003年,Bhat与Dham[3]基于周期性地磁场假设,证明了磁控卫星的可控性:当卫星沿非赤道轨道运行时,地磁场方向会随卫星位置改变而不断发生变化.这种变化使得磁控系统不可控方向也在不断变化,确保了磁控卫星的可控性.随后,Smirnov等[4]证明了在偏离平衡点较小时,可利用两轴磁控实现卫星稳定姿态控制.Yang[5]基于线性时变系统理论,证明了在卫星惯量满足一定条件时,可实现磁控卫星稳定姿态控制.

地磁场模型精度是决定所设计磁姿态控制系统能否成功实施的另一个关键因素.目前,最精确的地磁场模型为国际地磁参考场(IGRF模型),由国际地磁与气象学协会(IAGA)于1968年提出,此后每五年更新一次,目前为第13代[6].IGRF-13采用13阶球谐函数模型,结构复杂,通常适用于数值仿真过程.而对磁控算法的理论分析,学界通常采用偶极子假设.常用的偶极子模型有倾斜偶极子模型、直接偶极子模型以及简化偶极子模型[7].基于偶极子假设并忽略地球自转的影响,卫星所处地磁场会随卫星轨道运动而周期性变化.同时,也可采用更高阶球谐函数进行更精确的理论分析[8,9].

本文参考了前人的综述文章[10-13],沿用了文献[11]的分类结构,整理综述了自20世纪60年代以来卫星尤其是微小卫星所采用的主要磁姿态控制方法和算法,包括飞轮起旋、卸载,被动以及主动磁姿态控制算法,重点关注主动磁姿态控制算法的发展.其中主动磁姿态控制算法包括B-dot等主动磁阻尼算法,磁控与自旋、定转速飞轮、重力梯度力矩结合的算法以及纯磁控算法.最后,本文对各类磁控算法进行了总结与展望.

1 飞轮起旋与卸载

1.1 飞轮起旋

根据动量矩守恒原理,当飞轮的动量矩变化时会改变卫星的动量矩.目前主要有两类磁控算法用于飞轮起旋问题[14].

第一种方法首先利用磁力矩器与飞轮实现卫星稳定控制.此阶段磁控制律可采用PD控制律.卫星稳定后加速飞轮至目标转速,利用磁力矩器维持卫星姿态稳定[14,15].另一种方法是在卫星实现稳定控制前起旋飞轮,再利用磁力矩器与定转速飞轮稳定卫星.Chang等人在姿态获取阶段起旋俯仰轴飞轮,并使用B-dot控制律阻尼卫星角速度[14].该方案可更快实现稳定控制.研究表明,在B-dot控制律下,卫星姿态误差会以指数形式进行收敛[16].Meng等人设计了两种用于飞轮起旋的磁控律[17]:

(2)

(3)

1.2 飞轮卸载

工程中磁控制系统常用于飞轮角动量卸载.飞轮可抵抗环境干扰力矩的影响,实现卫星高精度姿态控制.但同时,由于一些常值干扰力矩的影响,如气动力矩,飞轮的转速可能会持续增加.当上升至最高转速时,飞轮将不能提供有效的控制力矩.需在飞轮转速达到其上限值前进行角动量卸载.常用的卸载方法有喷气卸载,磁卸载等.但喷气卸载需消耗卫星燃料.而磁卸载可利用电能进行卸载,且使用寿命长.

1961年,White等人[18]提出了叉乘磁卸载控制律,在磁控卫星中应用广泛[19-21],具体形式为:

m=kΔhw×B

(4)

其中k为控制增益,Δhw为飞轮角动量与目标角动量差值。通过该控制律,磁控力矩可卸载垂直于地磁场强度矢量B的角动量分量.通常,当Δhw与地磁场矢量的夹角足够大时(如夹角处于45～135度之间),才启动磁力矩器卸载,以防止垂直于Δhw的磁力矩分量过大对卫星产生不利影响.该控制律也可采用bang-bang控制形式计算所需磁矩[22].

针对叉乘控制律,后续文献进行了大量研究.Camillo与Markley[22]推导了叉乘控制律解析分析公式.该公式可用于增益系数k的初步选取.Ninomiya等人[23]对叉乘控制律进行了改进,使得控制律可同时实现飞轮角动量卸载与卫星章动阻尼.Hablani[24]使用线性极点配置方法,对叉乘控制律增益系数进行设计.针对冗余配置的飞轮系统,Lebedev[25],Hogan与Schaub[26]设计的叉乘控制律可确保每个飞轮的转速都卸载到零值附近.Trégou⊇t等人[27]与Avanzini等人[28]改进的叉乘控制律可在磁卸载的同时保证姿态控制律的渐进稳定.

一些优化方法也被用于飞轮磁卸载控制律设计.Glaese等人[29]设计了能量最优磁卸载控制律.Flashner与Burns[30]提出了一种基于单元映射方法的离散磁卸载控制律.该控制律基于周期性磁场假设,可离线设计优化方案.Steyn[31]基于LQR方法,通过最小化目标函数

(5)

实现了磁卸载控制律的优化.其中hw为飞轮角动量,Q,R为权重矩阵.Giulietti等人[32]构建了结合时间最优与能量最优的目标函数,即:

(6)

其中a为调节机动时间与能量消耗比例的权重系数.通过最大化目标函数,文献[32]给出了包含参数a的磁卸载控制律.此外,H∞方法也被用于磁卸载控制律优化[33].

磁卸载也可结合其他卸载方法提高效果.Chen等人[34]将磁卸载与喷气卸载组合,节省了喷气卸载的燃料消耗,同时提高了卸载速度.Burns与Flashner[35]利用重力梯度力矩、磁力矩、气动力矩三种环境力矩,设计了具有自适应特性的磁卸载控制律.

其他方案如模型预测方法[36],被动阻尼方法[37],点映射技术[38,39]等均可应用于磁卸载控制律设计.

2 被动磁姿态控制

被动磁姿态控制系统结构简单,性能可靠,不消耗卫星能源,常应用于设备有限且控制精度要求较低的卫星.其通常包括永磁体与磁滞棒两个组件.其中永磁体用于控制卫星指向,使其大致沿所处地磁场方向.磁滞棒通过磁化作用,可起到角速度阻尼作用.二者结合可实现低精度稳定姿态控制.

被动磁姿态控制系统最早于1960年应用于美国海军通讯试验星[40].通过被动磁控与机械消旋设备,该卫星成功实现了角速度阻尼与稳定指向.1960年6月,该项目另一颗试验星Transit 2A成功发射.该卫星仅凭借被动磁姿态控制系统实现了稳定控制[40].第一颗由大学自主研发的被动磁控卫星Injun 3于1962年成功发射入轨[41].此后,更多被动磁控卫星任务成功实施,如ESRO-1A (1968), ESRO-1B (1969), Azur (1969), Exos (1978), Magion (1978)[42].

随着星载计算机与控制设备的发展,被动磁姿态控制系统已不能满足卫星任务高精度与多样化需求.至20世纪70年代中期,被动磁姿态控制系统逐渐被主动控制方法替代.直到微小卫星技术的兴起,被动磁姿态控制系统再次受到学者关注.其满足了微小卫星质量、空间以及设备成本的限制,在一些大学自主研发的试验星或演示卫星中应用广泛.1990年,四颗采用被动磁控的微小卫星被送入太空[43].此后,更多应用被动磁控的微小卫星相继发射[42,44-50].

被动磁姿态控制原理简单,无需设计复杂的控制算法.目前学者更多关注主动磁姿态控制算法设计.

3 主动磁姿态控制

3.1 主动磁阻尼控制

当卫星角速度过大时,部分星载仪器如星敏感器无法正常使用,需使用星载设备降低卫星角速度至一定阈值.与运载器分离、执行变轨等机动操作或是设备故障均可能使角速度过大,因此,角速度阻尼是卫星姿态控制的必需过程.虽然喷气控制,飞轮控制等方法均可阻尼角速度,但喷气控制会消耗卫星燃料,飞轮控制易饱和.相比之下,磁阻尼控制不仅节省能源,还具备性能可靠,成本低廉等优势,在各类卫星中应用广泛.

Stickler 与Alfriend[19]提出了著名的主动磁阻尼算法“B-dot”控制律.该控制律最早出现在1972年[51],利用地磁场导数信息进行角速度阻尼,具体表达式为:

(7)

(8)

其中dB/dt为地磁场强度矢量相对于惯性系的导数,式(7)可表示为:

(9)

由于地磁场强度矢量在惯性系中变化的角频率仅为轨道角速度两倍,而通常在阻尼过程中卫星角速度较大,因此式(9)右侧第一项可近似为零.故式(9)可进一步简化为:

m=k·ω×B

(10)

卫星转动动能E的时间导数可表达为:

(11)

从上式可看出,采用B-dot控制律可有效减小卫星转动动能,实现角速度阻尼.

B-dot控制律具有很强的鲁棒性,通常利用当前时刻与前一时刻磁强计测量数据进行差分便可有效阻尼角速度.同时,B-dot控制律可转化为bang-bang控制形式,适用于实际工程问题[52].基于等式(9)的假设,B-dot控制律可以指数形式进行收敛[53,54],具体收敛速度受轨道倾角等因素影响[54].

B-dot也存在缺点.首先在阻尼精度方面,由于在上述分析中忽略了地磁场矢量相对于惯性系的时间变化率,即地磁场变化项,该项会对最终阻尼精度产生较大影响.研究发现,B-dot控制律最终会有约二倍轨道角速度的误差[55].同时,剩磁等干扰力矩会进一步降低阻尼精度.为克服地磁场变化项等带来的不利影响,学者们对B-dot控制律进行了改进[56-61],其中大部分变形基于等式(9).该变形可阻尼卫星角速度至零,但同时需要角速度测量数据,提高了测量设备需求.

为减少测量设备,Desouky与Abdelkhalik[62]基于地磁场数据对角速度进行等效计算,给出了改进的B-dot控制律.该控制律可保证磁力矩器需产生的磁矩m时刻垂直于卫星所处地磁场,提高了磁利用效率.蒙特卡罗仿真实验验证了该控制律的有效性.同时,该控制律可在一定程度上减少收敛时间,降低能源消耗.

Jin等人为惯量缺陷卫星(z轴惯量大于其他两轴)提出了垂直消旋控制律[63]:

(12)

该控制律可避免z轴长时间指向太阳而造成仪器损坏.

一些学者研究了增益系数k的选取方法.Avanzini与Giulietti[57]基于卫星轨道与形状特征,提出了一种增益系数调整方法,具体表达式为:

k=2ω0(1+sinζm)Jmin/‖B‖2

(13)

随着仪器设备与微小卫星技术的发展,B-dot控制律也发展出了适用于纳卫星、立方星的方案[65-70],如嵌入式磁线圈控制等.同时,新型磁阻尼方案如反馈阻尼控制律[71]也相继提出.但由于B-dot的简便性与鲁棒性,其仍是目前乃至未来很长一段时间磁阻尼算法的首选.目前磁阻尼算法体系已较为完备,要取得较大研究进展十分困难.

3.2 组合磁姿态控制系统

由于磁姿态控制系统无法施加独立的三轴控制力矩,其通常结合其他设备与方法实现高精度稳定控制,如自旋、飞轮、重力梯度力矩等.

3.2.1 磁控与自旋结合

磁控与自旋结合克服了磁控的固有缺陷,同时具有低功耗、低成本、高控制精度等优点,因此应用广泛,也是目前磁控卫星的主要控制方案之一.通过围绕最大惯量主轴旋转,自旋卫星可获得自旋稳定性.若无外界干扰,自旋卫星可在惯性空间中维持稳定.但由于太阳光压力矩等的影响,自旋卫星会发生章动,需采用其他控制方法对自旋卫星的旋转轴指向与转速进行控制,而磁控则是首选.

第一颗磁控与自旋相结合的卫星发射于1960年[2].此后,该方案被广泛应用于各类卫星任务.其中由Shigehara[72]提出的bang-bang控制律应用广泛.该控制律采用特定开关函数实现磁力矩器磁矩的正负控制,具体公式如下:

(14)

其中mj为沿卫星本体系坐标轴ej的磁矩大小;j=1,2,3;mj的幅值为m0;Δh为当前卫星角动量与目标角动量差值.该控制律可使卫星沿特定轴自旋,并调整自旋轴的惯性空间指向.该方案也广泛应用于立方星等微小卫星[73].

Crocker 与Vrablik[74]提出了可使卫星自旋轴z轴垂直于太阳矢量的bang-bang控制,即:

(15)

其中e为卫星自旋轴,s为本体系下太阳方向矢量.bang-bang控制还可与B-dot控制律结合解决自旋卫星章动问题.Holden 与Lawrence[75]基于李雅普诺夫方法设计了章动控制律,该控制律仅使用自转轴方向磁力矩器进行控制:

mz=m0sign[(C-A)Byωx-(C-B)Bxωy]

(16)

其中A,B,C为卫星三轴转动惯量;ωx,ωy及Bx,By分别为卫星角速度与地磁场强度矢量沿卫星本体系x,y轴的分量.该控制律不仅适用于轴对称卫星,对非轴对称卫星也有较好控制表现.Ovchinnikov 等人[76,77],Roldugin 与Testani[78]基于B-dot提出了简化控制律,利用磁场导数信息即可完成章动阻尼:

(17)

该控制律可使用一轴磁力矩器完成控制.Zavoli等人[79]分析了控制律(17)的具体性质,包括全局渐近收敛性质与自旋轴指向等.需要注意的是,由于该控制律所施加的控制力矩垂直于自旋轴,因此不能使卫星起旋.Ovchinnikov 等人[76]提供了一种卫星起旋控制律:

m=k(By,-Bx,0)

(18)

该控制律可产生沿自转轴方向的控制力矩,但同时会引入沿其他两轴的干扰力矩,需通过控制律(17)消除.针对自旋卫星起旋问题, Thomson[80]提出了“Y-Thomson”控制律,利用当前转速与目标转速差值对卫星转速进行控制.Creamer[81]基于B-dot控制律提出了另一种自旋卫星控制方法,具体形式为:

(19)

其中ωd为卫星期望转速.该控制律可有效阻尼卫星初始角速度,使得卫星按照所设定角速度旋转.Cubas等人[82]对该控制律的稳定性,收敛时间,自转轴指向以及控制精度进行了详细分析,并在考虑实际工程限制条件下进行了仿真,验证了控制律的可靠性.

可利用卫星当前角动量与目标角动量差值进行控制律设计.Avanzini等人[83]利用本体系与惯性系下的角动量差值,分别控制卫星角速度与自旋轴指向.此外,Avanzini等人[84]利用投影方法,即将角动量差值投影至与地磁场矢量垂直的平面,设计了另一种控制律:

T=k(I-BBT)Δh

(20)

基于文献[57]的分析方法,文中提供了增益系数k的选取方法.De Ruiter[85]同样利用投影方法,融合了章动阻尼、起旋以及自转轴指向等多个控制律,设计了应用于纳卫星的磁控方案.文中利用李雅普诺夫方法,证明了即使在两轴磁力矩器失效以及磁力矩器饱和等限制下,控制律也可保证渐进稳定.在考虑各种扰动以及设备故障等情况下,控制系统表现均能满足任务需求[86].该控制律已被成功应用于纳卫星ESTCube-1[87].

卫星可携带的能源有限,对于装备太阳能帆板的卫星,需尽快将电池板对准太阳.You等人[88]基于投影方法提出了一种太阳获取控制律,具体形式如下:

(21)

其中L为卫星角动量,l为其单位矢量,k1,k2为相关增益系数,θ=arccos(-sz),下标z表示该矢量沿本体系z轴的分量(z轴为其自旋轴).卫星首先进行角速度阻尼,然后切换至指向控制律,利用太阳敏感器读数实现太阳指向.Chasset等人[89]介绍了太阳获取控制律在具体卫星任务中的应用.利用太阳矢量与卫星本体系z轴夹角以及目标转速,文中构建了包含指向信息与转速信息的目标转速,通过投影方法实现了太阳获取.

Alfriend[90]利用地磁场信息以及卫星滚转角构建闭环控制律:

(22)

其中φ为1-2-3转序下相对于轨道坐标系的卫星滚转角.使用多时间尺度方法,文中对控制律的渐进稳定性进行了分析,通过与数值仿真以及Floquet理论对比,对控制律进行了验证.同时,文中分析了控制律对干扰力矩的鲁棒性.Wheeler[91]使用沿自旋轴方向的单轴磁线圈,利用卫星姿态、角速度与磁场信息构建反馈函数,实现了卫星稳定控制.Ovchinnikov与Roldugin[92]使用单轴磁力矩器,设计了可使小卫星在轨道平面内任意方向旋转的控制律.Ergin 与Wheeler[93]利用卫星姿态误差与地磁场信息,使用固定时间间隔内的恒定控制力矩设计了磁控制律.Renard[94]比较了在轨道偏心率,地球自转等影响下,仅使用沿自旋轴方向单轴磁线圈,不同控制律的表现.结果表明,基于轨道周期进行磁矩极性转换可实现较好鲁棒性.

Cheon等人[95]利用星载地磁场模型,设计了仅使用磁强计与GPS信息的磁控制律,其具体形式为:

(23)

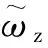
Junkins 等人[96]基于庞特里亚金最值原理,给出了控制自旋轴指向的时间最优机动设计方法.Sorensen[97]使用LQR方法对所需磁矩进行设计.

自旋卫星磁控制律时至今日仍在推陈出新[98,99].但自旋卫星的高速旋转特性不利于实施优化方法,同时相关研究也较为成熟,难以实现大突破.

3.2.2 磁控与定转速飞轮结合

当一轴飞轮以一定转速旋转时,会为卫星提供陀螺稳定性,使飞轮轴向保持在轨道法向方向,该类卫星称为偏置动量卫星.此类卫星无需高速旋转,降低了设备及卫星惯量要求.加入磁控可进一步提高偏置动量卫星控制精度,使卫星姿态误差渐近收敛.由于飞轮在轨道法向提供了足够的稳定性,磁控偏置动量卫星甚至可在赤道轨道实现稳定控制.

偏置动量卫星也需进行章动阻尼.Stickler与 Alfriend[19]使用控制律(22)进行章动与进动控制.Goel 与Rajaram[100]对该控制律进行改进,应用于近赤道轨道卫星,并给出了时间响应表达式.Hablani[101]改进了控制律(22),提供了增益系数选取方法.同时,Hablani[102]还考虑了非圆轨道下章动与进动控制,给出了控制律进一步改进形式.Pulecchi 等人[103]对Hablani改进的控制律进行了详细的性能分析.Tsuchiya 与Inoue[104]在控制律中添加积分项,提高了控制力对干扰力矩的鲁棒性.

PD控制是偏置动量卫星常用的磁姿态控制方案之一.其基本形式为[105]:

(24)

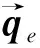
m=kω

(25)

下的运动问题.Ovchinnikov 等人[16]提出了可使卫星在轨道平面内实现任意指向的磁控制律,具体形式为:

(26)

其中α为3-1-2转序下第一个姿态角,α0为其目标值.文中分析了重力梯度力矩干扰下卫星的运动,并给了运动形式.

Wang与Shtessel[109]基于滑模控制提出了偏置动量卫星磁控制律.通过解耦俯仰轴运动方程,设计了针对滚转偏航轴及俯仰轴两种滑模控制律,通过开关转换函数,实现了bang-bang控制.

基于LQR方法的优化方案也可用于偏置动量卫星控制律设计.早在1993年,Pittelkau[110]就基于LQR方法,提出了针对极轨道卫星的最优控制律.文中建立了干扰力矩周期模型,通过求解Riccati方程得到了最优控制增益.此后,Lagrasta与Bordin[111]同样使用LQR方法设计了磁控制律,该控制律可抵抗恒定干扰力矩.Guelman等人[112]介绍了应用于小卫星Gurwin-TechSAT的优化控制律.同时,文中提到了一种类似于控制律(22)的bang-bang控制,具体形式为

(27)

其中Bmeas与Bexp分别为磁强计测量与星载磁场模型计算得到的地磁场强度矢量.Pulecchi等人[113]提出了适用于星载计算机的离散LQR方法.

偏置动量卫星的陀螺稳定性质克服了磁控固有缺陷,同时其设备简单,控制精度高,自上个世纪以来应用广泛,并不断与新技术融合[119-122].后续关于磁控偏置动量卫星的研究会多集中于优化方法应用,如时间最优机动方案设计等.但偏置动量轮体积较大,应用于纳卫星,皮卫星等存在一定局限性,需做进一步研究.

3.2.3 磁控与重力梯度力矩结合

重力梯度力矩也可为卫星提供被动稳定.通过重力梯度杆等装置,地球重力可为卫星提供一轴稳定力矩.该方式在上个世纪卫星任务中应用广泛.同时,为防止卫星绕重力梯度杆旋转等,需利用磁力矩对卫星进行姿态控制.

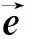
(28)

同时,文中还设计了控制律(27)的实施阈值,即当误差大于一定阈值时该控制律才会施加于卫星,以防止卫星因仪器测量与执行误差在平衡点附近发生摆动.Lovera与Astolfi[125]证明了PD控制律的稳定性.同时,基于磁场平均化理论以及小角速度假设,Lovera与Astolfi[125]证明了PD控制可指数收敛.

通常控制律得到的理想控制力矩Td会使用投影方法计算所需磁矩m.此时施加于卫星的实际力矩T根据式(1)进行计算.由于T须垂直于地磁场矢量,因此与理想控制力矩Td存在一定误差.Arduini与Baiocco[126]针对重力梯度卫星,提出了两种可使Td与T误差最小化的方法.其中一种是最小化二者欧拉二范数,另一种则是使T两轴分量与Td一致,在满足T垂直于地磁场矢量的限制下,设计其第三轴力矩分量.

Bak等人[127]基于滑模控制提出了姿态阻尼控制律,基于LQR方法提出了三轴稳定控制律,两种控制律均被应用于重力梯度卫星Orsted.文中对B-dot控制律进行了改进,添加了永磁体部分mconst,即

(29)

其中永磁体部分用于控制重力梯度杆指向.控制律(29)也被应用于立方星姿态控制[128].同时,Gravdahl[128]考虑了当重力梯度杆未正确指向时使用磁控制律进行故障处理,通过仿真证明了控制律可靠性.Leonard[129]同样基于LQR方法,提出了PD控制增益系数选取方法.Zhou等人[130]考虑了在重力梯度杆未完全展开情况下,使用滑模控制为小卫星BUAA-SAT设计控制律,该控制律可抵抗惯量不确定性的影响.Steyn[131]为重力梯度卫星设计了模糊控制律,并与LQR方法设计的控制律进行了比较,通过仿真验证,证明了模糊控制律具有更好控制表现.磁控重力梯度卫星还可与自旋结合进一步提高控制表现[132].

重力梯度卫星磁控制律发展也较为成熟,近期相关研究多依据具体卫星任务开展,如Arefkhani等人[133]基于LQR方法提出了优化控制律,该控制律可使理想控制力矩Td垂直于地磁场矢量,提高了磁利用效率.Erturk[134,135]基于LQR方法为3U立方星设计了周期控制律.

磁控与其他方法结合的算法,例如与气动力矩结合[136,137],与喷气控制结合[138,139],与飞轮控制结合[140,141]等,文中不再具体展开.这些方案均具有各自的局限性.喷气与飞轮控制结构复杂,未充分利用磁控优点.气动力矩需设计复杂气动外形.同时,一些新方法,如磁控与电磁力结合,目前仍在完善发展中.

3.3 单独磁姿态控制系统

2003年,Bhat与Dham[3]证明了磁姿态控制系统的可控性,为后续纯磁控发展奠定了理论基础.此后,纯磁控逐渐成为学者研究热点.

3.3.1 PD反馈控制

PD控制是纯磁控卫星优先考虑的控制方法.但由于磁控固有控制缺陷,传统PD控制不能直接应用于纯磁控卫星,需进行改进.基于平均化理论,Lovera与Astolfi[142]为纯磁控卫星提出了改进PD控制律:

T=-(ε2k1q+εk2Iω)

(30)

其中ε为使系统可渐进稳定而定义的缩放参数.该控制律通过投影方法计算所需磁矩.控制律的指数收敛性质在文中被证明.另外,文中还针对磁力矩器饱和问题设计了改进控制律,证明了其稳定性.Lovera与Astolfi[142]还提出了仅利用姿态四元数进行反馈控制的磁控制律(下文称为四元数反馈控制律).该控制律只适用于近圆卫星.同时,Lovera与Astolfi[143]在控制律(30)基础上进行了改进.Giri等人[144]使用人工小参数方法,证明了PD控制律的稳定性不依赖初始状态,在增益系数满足一定条件时该控制律均可以指数形式收敛.

控制律(30)的增益系数存在一定限制.Rossa等人[145,146]揭示了只有当缩放参数ε在一定阈值下时,才可保证该控制律渐进稳定.通常该阈值需足够小.增益系数的限制与磁控固有缺陷有关.由于控制律(30)采用投影方法计算所需磁矩,其实际控制力矩T与理想控制力矩Td存在一定误差.若控制力矩T过大,误差也会随之增大,只有当控制力矩足够小时,卫星才可通过迭代逐步收敛至平衡位置.

通常纯磁控律对惯量不确定性等干扰较为敏感[147],因此纯磁控律增益系数选取是控制律设计关键.最简单的方法是试错法,即不断调整增益系数直至控制律能够渐进收敛.该方法效率低,且可搜索空间有限.Ovchinnikov 等人[148]基于小参数假设与Floquet理论,提出了一种增益系数选取方法.Ovchinnikov 等人[149]还根据时间响应速度,提出了调整增益的半解析方法.同样基于Floquet理论,Mahfouz等人[150,151]在目标姿态附近对卫星动力学模型进行线性化,通过数值优化,实现了最优增益系数选取.Thepdawala[152]将该方法应用于神经网络训练,使得卫星可在线优化增益系数.Bruni与Celani[153]通过最小化误差四元数收敛时间,提出了PD增益系数优化方法.同时,文中构建了一种“最小-最大”问题,以确定在最差初始条件下的最短收敛时间.Bruni与Celani[154]将该方法应用于四元数反馈控制律增益系数选取.此外,PSO等迭代优化方法也可用于增益系数优化领域[155,156].同时,可利用如平均控制等理论[157,158]设计较为鲁棒性的磁控制律.

为消除角速度叉乘项对动力学模型的耦合影响,一些学者对卫星模型做了球形假设,即卫星三轴转动惯量相等.Reyhanoglu等人[159,160]将PD控制律与利用四元数信息进行反馈的控制律应用于球形卫星.Inamori等人[161]利用垂直于磁场矢量的两步旋转,实现了使用磁力矩器进行近赤道轨道球形卫星姿态控制.Smirnov[162],Bushenkov等人[163]构建的控制律为磁强计测量数据的函数.该控制律使用磁强计与磁力矩器进行球形卫星稳定控制.仅使用磁强计作为测量仪器可进一步减小姿控系统质量.磁强计测量数据经过滤波可获得卫星姿态与角速度信息[164].同时,Sugimura等人[164]利用奇异鲁棒性逆矩阵求解卫星所需磁矩,具体公式为:

(31)

其中B×为地磁场强度矢量B构成的叉乘矩阵,即:

(32)

该方法已应用于小卫星REIMEI[165].

实际卫星任务中,磁力矩器产生的磁矩会影响磁强计的测量结果,因此二者需交替使用.Desouky与Abdelkhalik[166]分析了磁力矩器与磁强计占空比对控制精度的影响.研究发现,占空比增大会降低控制精度,增加功耗.Celani[167,168]考虑了不同占空比限制,设计了离散控制策略.Desouky与Abdelkhalik[169,170]通过减少磁强计测量频率提高了磁控系统表现.Xu等人[171]考虑了磁力矩器执行延时情况下磁稳定控制问题.相关卫星任务也进行了纯磁控尝试.Gurwin小卫星尝试在偏置动量非常小的情况下使用磁控进行姿态控制,但最终未能取得成功[112].其他卫星任务也进行了相关尝试,如TANGO卫星[172],GOCE卫星[173],但TANGO卫星使用了自旋稳定,GOCE卫星使用了气动力矩.

纯磁控卫星PD控制律不仅局限于控制律(30).Gulmammadov 等人[174]使用指向轴与目标方向误差角设计PD控制律,该控制律可使卫星具有更长通讯时间.由于纯磁控律对参数的敏感性,相同控制律对不同卫星并不具有普适性.因此,未来研究会针对控制律鲁棒性开展,并从工程实际角度对控制律进行提高.

3.3.2 滑模控制

1998年,Wang与Shtessel提出了可应用于纯磁控卫星的滑模控制律[175].由于其优异的鲁棒性能,此后基于滑模控制的纯磁控律逐渐受到学者们关注.

s=Iω+Kq

(33)

其中K为正定矩阵.Sofyali 与Jafarov[177]将滑模面进行简化:

s=ω+Kq

(34)

Sofyali 与Jafarov[178-180]在此基础上添加了积分项,提高了控制律鲁棒性.Ovchinnikov 等人[181]通过迭代方法更新滑模面具体形式,并利用时变增益矩阵,使得理想控制力矩Td近似垂直于地磁场矢量.通过采用更高阶非线性滑模面,滑模控制可进一步缩短收敛时间,提高鲁棒性[182,183].Schlanbusch 等人[184]采用线性最小二乘方法计算所需磁矩,提高了控制律表现.

3.3.3 优化算法

由于磁控力矩方向具有固有限制,因此结合此限制的优化方法也常用于磁控制律设计.其中LQR方法应用广泛.

Liang等人[199]考虑了机动时间问题,提出了一种模型预测控制律.在性能指标中添加时间积分项,并把自由终端时间问题转化为固定终端时间问题,可得到目标函数:

(35)

PD等控制律通常使用投影方法计算所需磁矩.但该方法磁利用效率较低,可使用优化方法提高磁利用效率.一种优化方法为在满足实际控制力矩T垂直于地磁场矢量限制下,最小化其与Td的欧拉二范数,其中Td为通过控制律计算得到的理想控制力矩.该优化方法可通过添加限制条件满足特定卫星任务需求[200].对惯量分布不均的卫星,上述优化方法可能会使得卫星惯量较小轴控制表现较差.因此,Wood与Chen[201]利用权重矩阵Q,对性能指标做了改进,即

(36)

其中Q为正定对角矩阵.通过调节Q各个元素值,卫星各轴控制表现均可有一定程度提高.

除上述较为常用方法外,如基因算法[202],滚动时域优化方法[203],伪谱法[204]等多种优化方法[205,206]均可应用于纯磁控律设计.通常,优化算法计算量较大,星载计算机不易实施.因此,未来优化算法发展会关注算法的高效性与实用性,使得卫星可快速有效实施在轨优化.

3.3.4 其他纯磁控方案

近些年如模型预测方法,自适应性方法等新型控制方法逐渐受到学者关注.

Silani与Lovera[12]提出了纯磁控卫星模型预测方法(MPC).通过建立预测模型,并基于当前控制序列,方法对一定时间间隔内卫星状态量进行预测.将预测结果与参考结果进行对比,最小化二者误差,方法可得到下一时间间隔内最优控制序列.重复上述过程,即为模型预测方法大致过程.该方法考虑了磁控方向限制,并具有较好鲁棒性.预测模型可为线性化动力学方程[207],也可采用非线性形式[208].但由于该方法需采用在线实时优化,对星载计算机要求较高,目前还未应用于实际卫星任务.相关算法应用,改进及未来发展情况在文献[209]中有具体介绍.

自适应性方法依托人工神经网络方法.通过在线学习,该方法可拟合实际动力学模型,具有很强鲁棒性,但计算量庞大,对星载计算机要求过高.尤其是对如微小卫星等计算资源有限的航天器,该方法并不实用.相关算法发展可参考文献[210-214].

4 结论

本文对飞轮起旋与卸载算法,被动及主动磁姿态控制算法等卫星磁姿态控制方法与算法进行了综述.磁控系统性能可靠、成本低,工程中常用于飞轮起旋与卸载,但该领域研究成熟,近些年新结果较少.被动磁姿态控制系统结构原理简单,无需设计复杂控制算法,但控制精度低,通常应用于精度要求较低的演示卫星或试验星,建立被动磁控卫星精确动力学模型是未来研究方向.主动姿态控制算法方面,主动磁阻尼算法及磁控与自旋、定转速飞轮、重力梯度结合的算法自上个世纪便被应用于卫星控制,理论研究成熟,后续研究可结合具体任务需求,利用优化方法提高算法性能,如优化偏置动量卫星机动时间等.纯磁控算法是目前研究热点.其中PD控制对参数不确定性与扰动较为敏感,因此算法鲁棒性及针对具体工程问题的研究是未来发展方向.基于各类优化方法的纯磁控算法,模型预测方法,自适应性方法具有较好鲁棒性,但计算量较大,需进一步提高计算效率以满足星载计算机性能限制.

磁姿态控制算法不仅适用于地球近地卫星,对木星探测器,也可结合磁控进行任务规划.磁姿态控制系统功耗低,能源可再生,可解决木星探测任务距离远,时间长的问题.目前对木星磁场的研究[215]还不成熟,具体控制算法需根据进一步磁场研究结果进行设计.