高阶Maggi方程的Birkhoff化及其辛算法*

薛冰 解加芳 张可心

(北方工业大学 理学院, 北京 100144)

引言

非完整系统是一类受到不可积微分约束的动力学系统[1],广泛应用于场论、机电动力系统、控制理论、工程科学等领域[2].20世纪80年代我国学者梅凤翔研究了带参数约束的一类可控系统[3]、变质量非完整约束系统.Maggi在1896年推广了拉格朗日第二类方程[4],对线性非完整约束系统得到一类动力学方程,后人称为Maggi方程[5],这些方程后来被推广到非线性非完整系统[6].Maggi方程是力学系统[7]各大运动方程的中间产物,对研究非完整系统的运动具有重要意义.

Birkhoff动力学理论是Hamilton动力学的自然推广,它是包括齐次Hamilton系统和非齐次Hamilton系统的更一般动力学理论,是最一般辛结构的局部实现,只有Birkhoff系统与一般辛几何结构之间才有一一对应关系.因此 Birkhoff 系统动力学[8]的研究对于完善和深化分析力学的理论体系具有重要意义, 尤其是对于非齐次 Hamilton 动力学系统的几何结构分析具有重要应用价值[9].本文针对非完整系统高阶Maggi方程,在其满足一定条件下,将其进行Birkhoff化。并通过一个算例验证上述理论分析的正确性,再分别采用Runge-Kutta方法和Birkhoff辛算法对其进行数值计算[10],并将数值结果进行比较,给出Birkhoff辛算法在长时计算时的优越性.

1 高阶非完整系统Maggi方程的Birkhoff化

设力学系统的位形由n个广义坐标qs(s=1,…,n)确定,系统受有g个理想m阶非完整约束[11]

(1)

其中

根据d’Alembert-Lagrange原理可以导出Maggi形式为:

(σ=1,…,ε)

(2)

式中Qσ为广义力,T为系统动能.

令

(ν=1,…,ε;k=1,...,n)

(3)

则方程(2)有形式

(4)

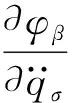
(5)

约束对初始条件的限制为:

(6)

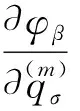
(7)

约束对初始条件的限制为:

(8)

将式(7)化为标准一阶形式,令

(s=1,…,n)

(9)

则式(7)可以写成形式

(10)

其中

aν=xν,σs=xn+s,…,

σ(m-2)n+s=x(m-1)n+s,

σ(m-1)n+s=hs(s=1,…,n)

(11)

为将式(10)表为Birkhoff形式,其阶必为偶数[9],即mn=2N,如果mn为奇数2N-1,可增加一个方程

(12)

使其成为偶阶.从而,要使高阶非完整系统的Maggi方程可表示成Birkhoff形式

(μ=1,…,2N)

(13)

即要求满足

(μ=1,…,2N)

(14)

设式(10)的2n个第一积分Iμ(t,a)彼此无关,即

(μ=1,…,2n)

(15)

(16)

根据Hojman方法,则式(14)的Birkhoff函数组Rμ由下式确定

(17)

Birkhoff量B为:

(18)

其中Gα需满足条件

(19)

2 Maggi方程的广义辛差分格式

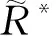
(20)

其中

(21)

假定方程组(20)的一种离散可以记为:

[∂tR(zi,ti)]i

(22)

式(22)称为式(20)的一个离散格式,如果它决定的格式Φ保持离散的K(z,t)辛格式,即

(23)

(24)

以及

(25)

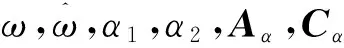
此映射为:

(26)

式(26)的Jacobi矩阵为:

(27)

映射α要满足

(28)

其中

当K与z无关时,根据式(27)和式(28)可以得到

(29)

且需满足下面的截面条件

|CαM+Dα|≠0

设Bα=Cα=0,则式(29)可成

(30)

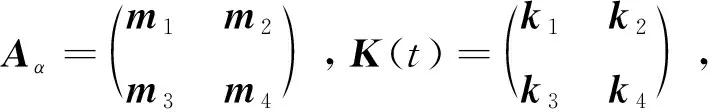
由式(30)可以得到

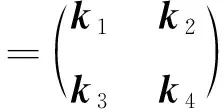
(31)

生成函数φ(ω,t,t0)=α(t,t0),可以构造广义Birkhoff辛差分格式.当步长τ>0足够小的时候,取

(m=1,2,…)

(32)

α1(zk+1,zk,tk+1,tk)

(33)

3 算例

假设某一力学系统的位形由2个广义坐标q1,q2确定,其系统动能为

(34)

且该系统受到1个2阶非完整约束:

(35)

(36)

显然式(36)有解:

q1=1-arctan(t)

q2=-3t·arctan(t)+2ln(t2+1)+t

由此可以构造Birkhoff函数Rμ,B如下[11]:

R2=0

R4=0

从而将该系统的Maggi方程可以Birkhoff化:

结合式(24)和式(25),我们可以确定生成函数φ(ω,t,t0),之后采用上述的Birkhoff广义辛算法式(32), 得到此 Birkhoff 系统的二阶K(z,t)离散格式[11-13].

对该题采用二阶K(z,t)算法和二阶Runge-Kutta算法进行计算.在计算过程中,先取如下初值:q1=1,C1=C2=1,取步长τ=0.01.并通过比较两种数值方法计算所得数值解和解析解q1=1-arctan(t)之间的相对误差来说明两种数值方法的差别.

对比图1和图2可以看出,Runge-Kutta方法在长期跟踪后与解析解有着大幅度的相对误差,而Birkhoff辛算法则相对误差非常的小.因此,Birkhoff辛算法结果更加精确.

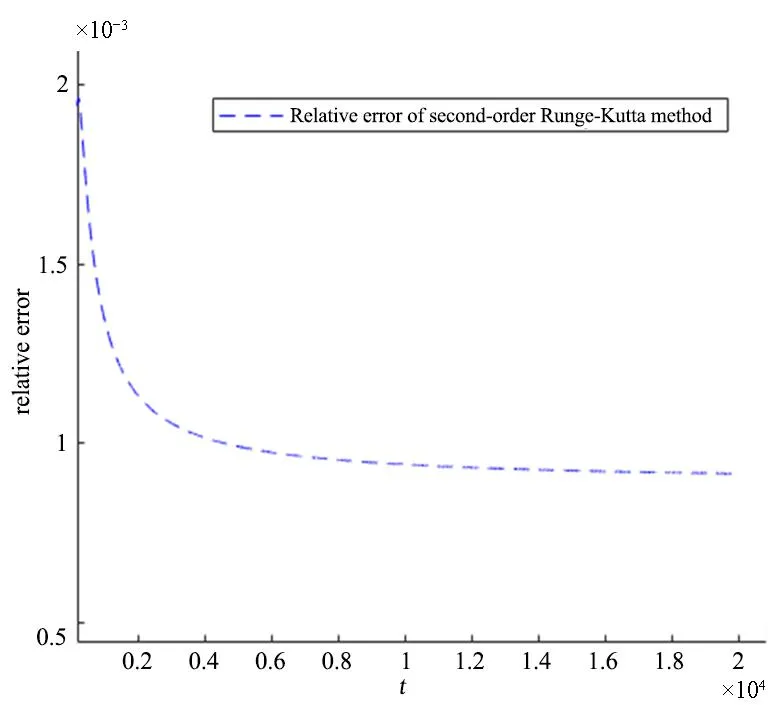
图1 二阶Runge-Kutta算法相对误差Fig.1 Relative error of second order Runge-Kutta algorithm

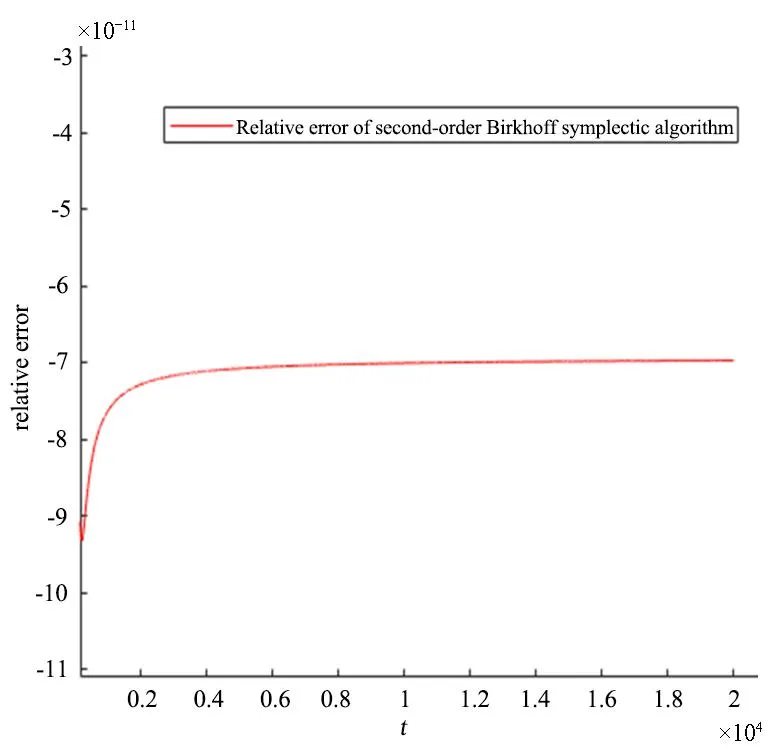
图2 Birkhoff辛算法相对误差Fig.2 Relative error of Birkhoff symplectic algorithm

4 结论

本文对一定条件下的非完整系统的高阶Maggi方程(2)先进行了Birkhoff化,得到广义Birkhoff方程(13),并针对该方程,应用Birkhoff广义辛差分格式与传统Runge-Kutta算法分别进行计算,比较两种算法,最后得出Birkhoff广义辛差分算法在求解非完整系统高阶Maggi方程中更加优越.