不可压缩超弹性球体中微孔运动的分岔和混沌*
马敏富 赵振涛 陈威屹 袁学刚,3†
(1. 北方民族大学 数学与信息科学学院,银川 750021)
(2. 大连民族大学 机电工程学院,大连 116600)
(3. 大连民族大学 理学院,大连 116600)
引言
橡胶、类橡胶等是典型的超弹性材料,被广泛应用于汽车、建筑、电子、航空航天等诸多领域,具有很好的减震或吸能作用[1,2].作为一种具有储能函数的非线性弹性物质,其本构关系可以完全由它们的应变能函数给出,如neo-Hookean、Ogden、Mooney-Rivlin和Yeoh材料模型等[3].特别地,neo-Hookean材料模型因其形式简单以及无条件稳定性等优点,为非线性弹性体动力学建模和求解提供了很大的便利[4,5].
当非线性材料和结构受到外部拉伸时,会出现空穴的生成、增长以及相邻空穴的贯通等现象,由此引起了众多学者的关注.其中,Polignone等[6]基于超弹性材料组成的球体,研究了微孔的生成和增长以及微孔的静态分岔问题.Yuan等[7]推导出微孔运动的二阶非线性常微分方程,并分析了微分方程解的定性性质,讨论了材料参数对微孔进行周期振荡的影响.Tang等[8]基于非线性动力学理论,研究了粘弹性材料组成的结构稳定性问题.任九生等[9]研究了周期载荷作用下不可压缩超弹性球体中的空穴生成问题,并对系统进行数值模拟,得出周期载荷的平均载荷与空穴运动之间的关系.Yuan等[10]对于超弹性材料组成的球形薄膜,推导出描述薄膜径向对称运动的二阶非线性常微分方程.详细讨论了在周期阶梯载荷作用下球形薄膜随时间产生的非线性周期振动并给出相应的数值模拟.近年来,随着非线性动力学理论的发展以及数值计算的进步,使得与超弹性材料相关的更复杂问题的求解成为可能.张弛等[11]研究了受轴向激励弹性支承梁的稳定性问题,在非线性弹性理论框架下推导控制方程,并对其进行数值模拟.Xu等[12]研究了一类不可压缩热超弹性材料组成的圆柱体的有限变形问题.利用边界条件等推导出隐式解析解,数值算例表明,圆柱体中部的径向变形几乎是均匀的,当轴向载荷较大时,两端附近的变形沿轴向变化较明显.曾青等[13]针对一类拟周期激励的分段非线性轧机辊系统,发现存在多种路径可以产生奇异非混沌吸引子并进行了证明,该研究为非光滑动力学系统中的混沌控制提供了相应的理论依据.Aranda-Iglesias等[14]研究了超弹性材料组成的圆柱结构的轴对称非线性振动,证明了圆柱壳的运动可以由周期到拟周期和混沌的变化,并讨论了参数对结构非线性振动的影响.张文等[15]针对一类单自由度齿轮动力学系统,将其动力学方程简化为二阶微分方程,通过打靶法得到嵌入混沌吸引子中的不稳定周期轨道,并利用OGY方法实现了混沌控制.同时考虑材料和几何非线性,Zhao等[16]研究了动态加载下粘-超弹性球壳的非线性动力学行为,根据变分原理和有限粘弹性理论推导出描述粘-超弹性球壳径向对称运动的耦合的积分-微分型方程,并发现材料的粘性系数改变时,系统的共振频率发生偏移,混沌和多周期振动交替出现.随后,Zhao等[17]又研究了动态载荷和结构阻尼对不可压缩超弹性球壳的非线性动力学行为的影响,并使用Melnikov方法对混沌运动进行了分析.此外,李双宝等[18]介绍了非光滑系统全局动力学Melnikov方法的研究进展.李冠强等[19]基于Duffing振子系统,对控制方程进行数值模拟,进一步揭示了对称系统到非对称系统的演变过程.
本文研究了周期扰动载荷作用下微孔的复杂动力学行为.首先,针对一类径向横观各向同性不可压缩超弹性neo-Hookean材料组成的球体,建立描述内部微孔径向对称运动的数学模型,并将其约化为二阶非线性常微分方程;其次,讨论了材料和结构参数对非线性系统平衡点的影响,并进行了定性分析;最后,结合数值算例分析了周期扰动载荷下微孔的拟周期和混沌运动.
1 模型建立
1.1 控制方程
基于弹性力学理论,描述弹性体运动的平衡微分方程为:

(1)
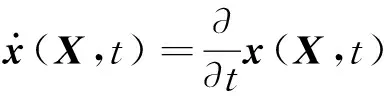
本文研究了在一类周期扰动载荷作用下,超弹性球体中心处微孔的径向对称运动.令(R,Θ,Φ)和(r,θ,φ)分别为初始构型和当前构型下的球体坐标.特别地,在球对称变形假设下,式(1)可以简化为如下的偏微分方程
(2)
在式(2)中,σrr(r,t),σθθ(r,t)是Cauchy应力张量的两个主值,分别为
(3)
其中,p(r,t)是待定的静水压力,F的主值由下式给出
(4)
本文假设球体由一类径向横观各向同性neo-Hookean材料组成,相应的应变能函数为[6]
(5)
其中μ是剪切模量,a≥0是反映各向异性程度的无量纲材料参数.
球体的外表面受到径向周期性扰动,并且微孔表面无约束,相应的应力边界条件为
σrr[r(ε,t),t]=0
(6)
其中,P(t)=p0+ηsinωt是与时间t相关的径向扰动载荷,p0为常值载荷,η为外激励幅值,ω为扰动载荷的外激励频率,A和ε分别表示球体的外表面半径和微孔的初始半径.
球体在时间t=0时处于未变形状态,则初始条件可以表示为
(7)
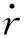
因此,描述在径向周期扰动载荷作用下超弹性球体的径向对称运动的数学模型由式(2)~式(7)给出.
1.2 模型求解
根据材料的不可压缩约束,有∂r(R,t)/∂R=R2/r2(R,t).等式两边关于R积分,可以得到
(8)
其中r1(t)=r(R1,t)≥0是与微孔半径相关的待定函数.根据式(7)和式(8),有
(9)
对球体的平衡微分方程以及初边值条件进行整理可得
(10)

为了便于定性分析,引入如下形式的无量纲变换
x(t)=r1(t)/A,δ=(A3-ε3)1/3/A,
(11)
其中,τ为无量纲时间.根据式(10),式(11),得到如下形式的无量纲方程
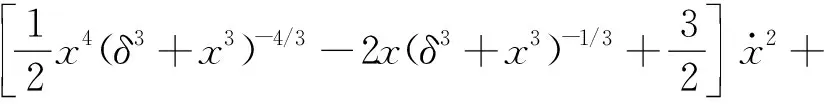
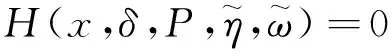
(12)
其中
(13)
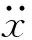
(14)
2 常值载荷
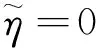
(15)
2.1 平衡点及其定性分析

Pcr+Mnx3+o(x3),(x→0+)
(16)
其中,Pcr是微孔生成的临界载荷.
令Mn=0,求得微孔分岔的临界材料参数a0,当a 图1 系统的平衡点曲线Fig.1 Equilibrium point curves of the system 进一步求得式(12)的首次积分 (17) 其中C是与初始条件相关的“能量常数”,S(x,δ,P)为系统的势能函数,具体形式为 (18) 对给定的材料参数,微孔在常值载荷作用下的非线性振动周期为 (19) 其中xmax对应微孔的最大半径. 给定初始条件时,系统可围绕任一势阱作周期运动,也可以同时围绕两个势阱作周期运动,且势阱与系统的中心相对应,如图2(a)、图2(b)所示.由图2(c)、图2(d)可知,对给定的材料参数,当微孔半径足够小时:(1)若a 图2 不同参数对应的势阱和等高线Fig.2 Well potential and contour lines corresponding to different parameters 当初值取在系统的中心附近时,通过时程曲线,相轨迹和Poincaré截面重点关注微孔围绕单势阱和两势阱的拟周期运动. 图3 不同扰动参数下中心附近的时程曲线和相轨迹Fig.3 Time response curves and phase diagrams near the center under different perturbation parameters 注意到,在周期扰动作用下,微孔表现出拟周期运动,Poincaré截面变为多个独立的封闭曲线,且单势阱和双势阱运动都有类似的表现,如图4所示. 图4 周期扰动下的Poincaré截面,(a) 单势阱运动,(b) 双势阱运动Fig.4 Poincaré sections under periodic perturbation of (a) one well potential and (b) double well potentials 图5 不同初始条件下的Poincaré截面Fig.5 Poincaré sections with different initial conditions 为探究微孔在鞍点附近的动力学行为,首先分析了鞍点附近时程曲线的变化,由图6可以看出,微孔在鞍点附近对扰动参数的变化更加敏感. 图6 不同扰动参数下鞍点附近的时程曲线Fig.6 Time response curves near the saddle point under different perturbation parameters 图7 不同扰动参数下鞍点附近的Poincaré截面和最大Lyapunov指数Fig.7 Poincaré sections and maximal Lyapunov characteristic exponents near the saddle point under different perturbation parameters 本文针对一类径向横观各向同性不可压缩neo-Hookean材料组成的球体,分析了周期扰动载荷对微孔定性行为的影响,通过对该问题进行数学建模和定性分析,得到的主要结论为: (1)在常值载荷作用下,讨论了材料参数和结构参数对微孔分岔行为的影响.结果表明,材料参数和结构参数都会导致系统的二次转向分岔现象,并且随着外载荷的增大,系统的平衡点个数出现“1-3-1”的变化情况.通过分析系统平衡点和势阱的变化情况发现,材料参数和结构参数影响微孔的分岔并影响其生长速率.特别地,存在临界载荷,导致结构刚度的明显变化,甚至产生振幅跳跃现象. (2)在周期扰动载荷作用下,基于二次转向分岔的讨论,给出了结构出现混沌运动的条件.特别地,不同的初值选择导致微孔具有完全不同的运动方式:① 初值取在中心附近时,发现微孔呈现拟周期运动;② 初值取在鞍点附近时,通过时程曲线、Poincaré截面和最大Lyapunov指数等方法发现微孔呈现混沌运动,并通过拟周期运动中出现的等势线破裂现象进行了解释.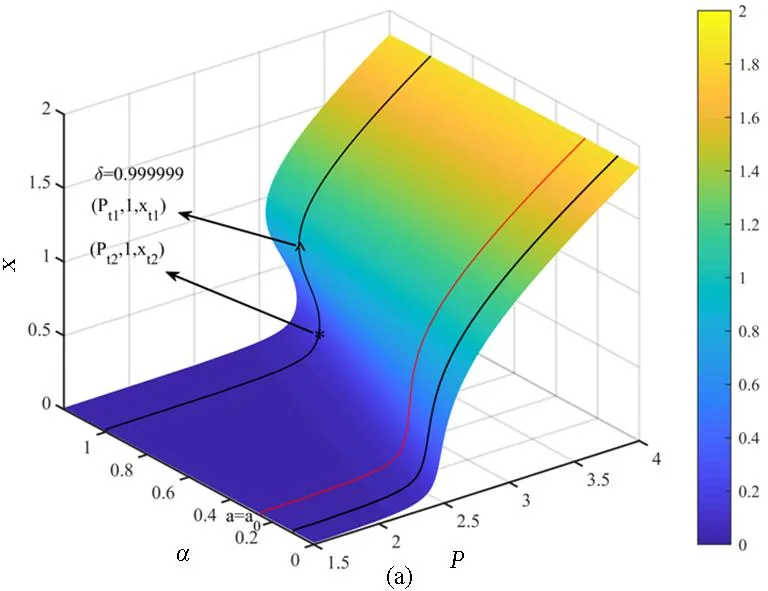
2.2 微孔的周期运动

3 周期扰动载荷

3.1 微孔的拟周期运动
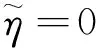

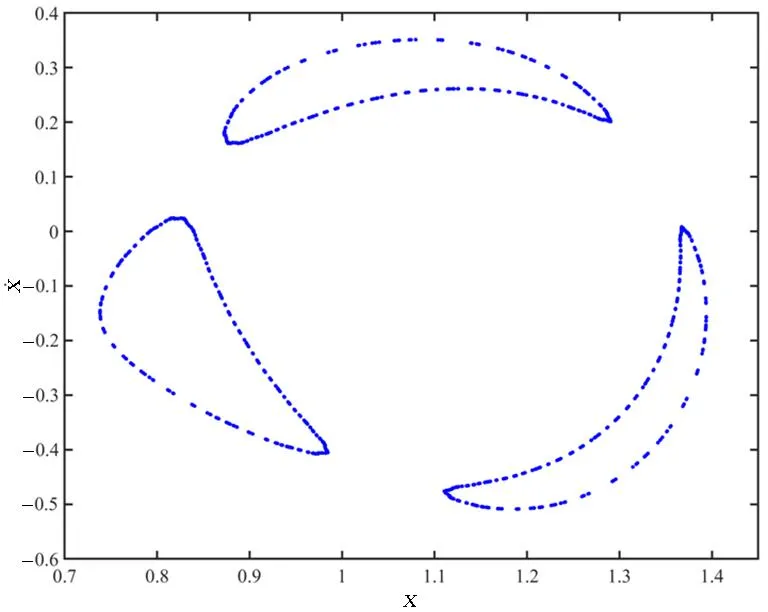

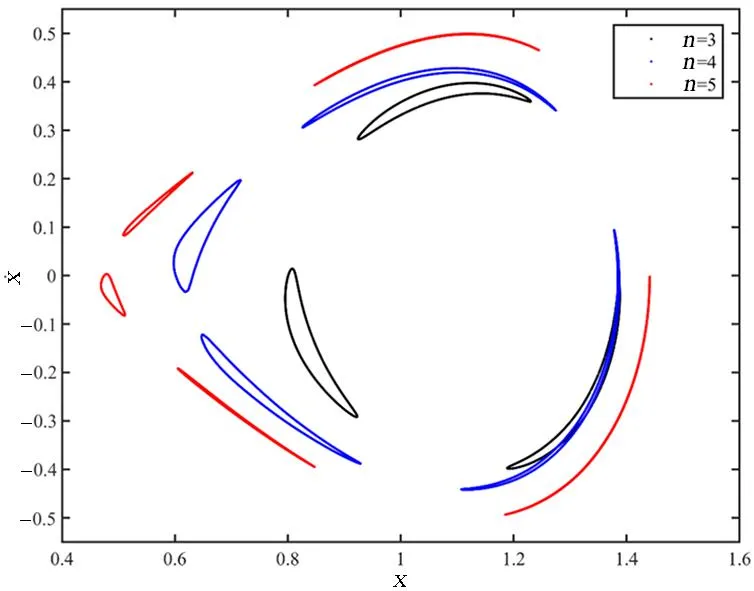
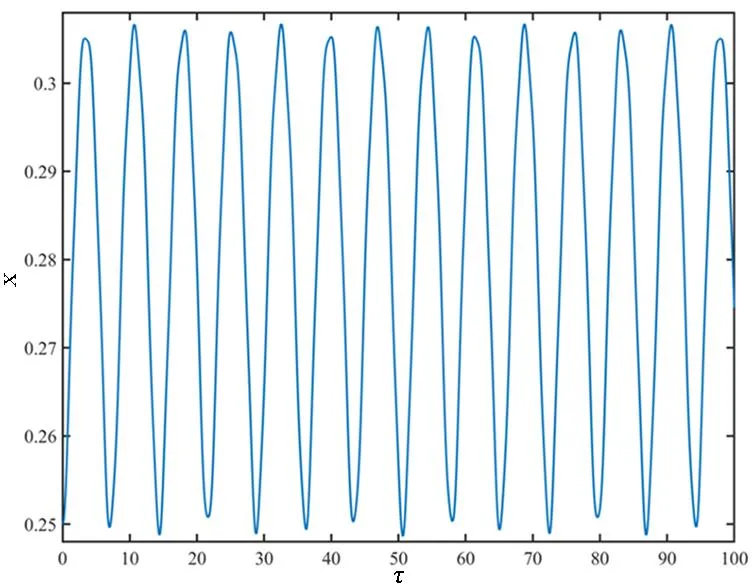
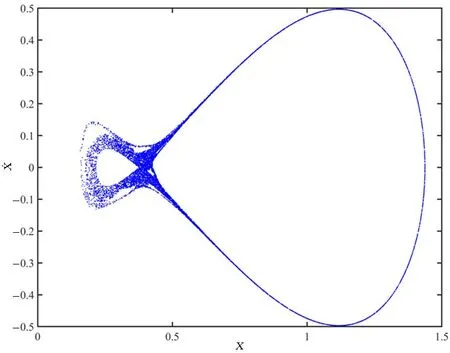
3.2 微孔的混沌运动
4 结论

