空间目标监视雷达大气折射修正技术研究

唐新杰 刘默然 乔建东 周晨

（武汉大学电子信息学院, 武汉 430072）

0 引 言

无线电波在大气层中传播时，由于大气介质不均匀分布的影响产生折射效应，使得电波射线发生弯曲、传播速度小于光速，导致雷达等测控系统在定位、导航时产生一定的偏差[1]。随着技术的发展和各种应用场景的需要，大气电波折射误差逐渐成为制约航天测定轨、空间目标监视等远程探测系统精度的重要因素，因此需要对测控系统探测目标测量值的折射误差予以修正。

现有的雷达折射误差修正方法可以分为射线描迹法、近似修正法和新型修正法三种，其中射线描迹法因为其精度高、实用性强等优点在研究和工程实践中都有广泛的应用[2]。折射误差修正精度不仅和选用的算法有关，还取决于选取的大气折射率剖面的准确度，学者们对此进行了大量的研究，通过模型或一些探测方法对大气折射率剖面进行建模。王宁等[3]引入径向基函数(radial basis function, RBF)神经网络算法反演大气折射率，验证了利用微波辐射计对流层电波折射进行修正的可行性；徐艳等[4]对中近程雷达应用场景中高精度目标定位误差进行了研究分析；张瑜等[5]针对下垫面复杂地区的三维大气结构，采用直接探测法和全国大气剖面模型组合的方法，有效提高了电波射线折射率分布的准确度；乔江等[6]对比研究了折射率剖面模型和映射函数在对流层折射误差修正中的精度表现；李川川等[7]结合微波辐射计和GNSS接收机研制的电波折射误差修正设备，实现了S波段雷达实时、高精度折射误差修正；刘琨等[8]提出了适用于高轨道目标折射误差修正的空间投影法和自适应网格法。

对于航天目标的雷达探测，电波传播主要受对流层和电离层两方面的影响。而对于P波段雷达而言，由于其频率相对较低，受电离层的影响更为显著，也明显比对流层影响更为严重。同时，低仰角相对于高仰角的误差更大，而低仰角意味着水平距离更远，其环境参数与探测点的环境参数差别也更大，因此对低仰角的误差修正就更为困难，这也一直是相关领域的难点之一。本文结合NRLMSISE-00大气模型对海拔60 km以下的对流层折射率剖面进行建模，并利用TEC数据同化的方式建立电离层现报模型，得到更精确的电离层实时信息，完成电离层折射率剖面的建模。在此基础上，利用射线描迹法对P波段雷达探测数据进行修正。与基于国际参考电离层（International Reference Ionosphere, IRI）模型的电离层折射率剖面相比，利用TEC数据同化现报模型得到的电离层折射率剖面可以极大提高修正精度。

1 建模方法

1.1 折射误差计算方法

射线描迹法从斯奈尔定律和费马原理出发，基于数学几何关系严格推导而来，具有较高的精度，因此成为工程中广泛应用的修正方法[9]。由于精度高，该方法也常被用来与其他的修正模型进行对比验证。图1给出了球面分层电波传播轨迹示意图，C为地心，O为测控站位置，T为目标位置。

图1 球面分层电波射线轨迹几何图形Fig.1 Geometry of spherical layered radio ray

高轨道远程目标一般沉浸于电离层之中的空间环境，由斯奈尔定理可以推导出雷达探测获得的目标视在距离Re计算式为

式中：rI为电离层底的高度；r0为测控站处的地心半径，r0=a+h0，a为地球半径，h0为测控站海拔高度；n为电波射线轨迹上变化的折射指数；r为目标至地心之间的距离；n0为地表处的折射指数；θ0为目标视在仰角。

测控站与目标之间地心张角φ的计算式为

目标真实仰角α0的计算式为

目标真实距离R0的计算式为

由上述式子计算得到距离折射误差∆R和仰角折射误差ε分别为

1.2 基于电离层现报同化模型的电离层折射率剖面

数据同化按照理论基础分类主要分为两类：一类是基于统计学的估计理论，如最优插值、卡尔曼滤波、集合卡尔曼等；一类是基于变分理论的方法[10]。卡尔曼滤波算法是常见的线性滤波和预测方法中的一种，是由匈牙利科学家Rudolph E.Kalman在1960年提出的。它是最早出现的顺序同化算法，一般认为它是顺序同化算法的理论基础。在近年的研究中，卡尔曼滤波算法越来越多地被应用于电离层数据同化中。

根据卡尔曼滤波理论，对观测资料的基本同化过程可表示为：

式中：为t+1时刻的背景场，由背景电离层模型给出；M为状态转换矩阵；为t时刻的分析场，即同化后得到的电子密度；为t+1时刻的背景场误差协方差矩阵；为t时刻的分析场误差协方差矩阵；Q为模型误差方差矩阵；为t+1时刻的分析场；K为增益矩阵，起到观测数据对背景场的调整作用；Y为观测场；H为观测算子，代表观测量与模型参量之间的关系；R为观测场误差协方差矩阵；为t+1时刻的分析场误差协方差矩阵。

本文采用目前被广泛应用于电离层研究的经验模型-IRI模型作为背景模型，版本为IRI2016。IRI由国际无线电科学联盟和空间研究委员会共同研发和维护，其数据来源于全球180多个电离层探测站的资料以及卫星的资料，主要模拟了电子密度、离子成分、离子温度、电子温度等一系列电离层参量的全球分布[11]。背景场的经纬度范围选取以雷达测站为中心的探测覆盖范围及周边区域，纬度为15°N~55°N，经度为70°E~140°E，水平格点分辨率设定为1°×1°，高度范围为60~1 500 km， 步长为10 km，因此背景场误差协方差矩阵Pb的大小为419 184 ×419 184。参与三维数据同化的观测数据主要为中国地壳运动观测网络(Crustal Movement Observation Network of China, CMONOC)的261个GNSS监测台站提供的电离层TEC数据，GNSS接收机的采样间隔为30 s。TEC是GNSS信号传播路径对路径上电子密度的线积分，所以观测算子H即为GNSS信号传播路径在电离层栅格中穿越的长度。

基于统计的协方差模型在估计背景误差协方差矩阵时会引入虚假相关，即在物理上不相关或空间上距离较远的状态变量之间存在虚假相关。为了降低虚假相关对同化过程的影响，提升同化效率，本文应用了协方差局地化(covariance localization，CL)方法[12]。CL方法采用一个基于距离的相关系数ρ与背景误差协方差矩阵作舒尔积，来替代原有的背景协方差矩阵。相关函数采用常用的GC (Gaspari-Cogn)五阶分段多项式函数，表达式如下：

式中：z为物理空间中两个格点之间的距离；c为长度尺度。

1.3 基于空间格点化获取的射线路径上折射率剖面

传统的射线描迹法忽略水平方向的不均匀性，往往采用垂直方向上的空间环境剖面来代表不同仰角下观测条件，即传统的射线描迹法适用于下垫面平坦、大气水平相对均匀的地区，而对于高目标低仰角的目标观测而言，电波实际传输路径较长，跨越的区域范围更大，经历的空间环境也更加多变复杂，因而不再满足水平均匀的假设条件[13]。

考虑到大气不均匀性产生的影响以及三维空间格点化大气高度分布形式，根据射线传播路径获取射线路径上位于不同空间栅格对应的空间环境参数值，进而计算得到更加真实的射线传播路径上的折射率剖面[14]。

三维空间中的电波射线的路径可以通过大地坐标系（L，B，H）和站心地平直角坐标系（E，N，U）描述，在站心地平直角坐标系中以雷达测站位置作为站心P0建立坐标系，电波射线轨迹以站心为起点向外延展到达目标，电波射线路径上的每个位置P可以用（EP，NP，UP）来表示，如图2所示。

图2 地心空间直角坐标系和站心地平直角坐标系Fig.2 Geocentric space and station center ground horizontal Cartesian coordinate system

NRLMSISE-00大气模型是由美国海军研究实验室设计研发的全球大气经验模型，描述了从地面到热层高度范围内（0~1 000 km）的中性大气密度、温度等大气物理性质，是目前使用最多的大气模型之一[15]。该模型在长时间的观测数据基础上建立并不断更新，主要数据源为火箭探测数据、卫星遥感数据和非相干散射雷达数据等，通过采用低阶球谐函数拟合大气性质随经纬度、年周期、半年周期、地方时的变化而建立的[16]。

本文使用NRLMSISE-00模型来描述和构建雷达电波射线经过的对流层大气环境，通过公式(12)可以计算得到对流层的折射率剖面：

式中：P为压强，hPa；T为大气温度，K；e为水汽压，hPa。

NRLMSISE-00模型和IRI模型是基于大地坐标系来计算获取全球空间环境参数的，为了保持空间匹配，NRLMSISE-00模型也按照经纬度1°×1°的栅格空间分辨率把雷达测站视野范围内的三维空间格点化处理，高度范围为0~60 km，步长为1 km。通过站心地平直角坐标系和大地坐标系的转换，可以将电波射线路径经过的每个位置投影到通过模型构建的空间栅格中，进而获取射线路径上相关的空间环境参数P、T、e、ne关于高度的分布（如示意图3所示），在此基础上进一步计算得到射线传输路径上的折射率剖面。电离层折射指数n与空间环境中电子密度的关系可表示为

图3 射线路径上不同空间栅格中环境参数选取Fig.3 Selection of environmental parameters in different spatial grids on the ray path

式中：ne为电子密度，el/m3；f为电波频率，Hz。

站心地平直角坐标系转换为空间直角坐标系的公式为[17]

空间直角坐标系转换为大地坐标系的公式为

式中：N为卯酉圈的半径，为第一偏心率，为椭球长半轴和短半轴。

2 结果分析

2.1 电子密度剖面同化模型效果比较

图4给出了2015-03-17T9:00LT的数据同化实例，其中图4(a)为背景模式的区域TEC分布结果，图4(b)为进行数据同化后的TEC分布结果。可以看出，数据同化方法实现了观测数据和背景模型有效融合，数据同化后的区域TEC分布相比IRI模型直接获取的结果展现了更为丰富的细节，更加符合实际。

图4 2015-03-17T9:00LT数据同化前后区域TEC分布的对比Fig.4 Comparison of regional ionospheric TEC maps using data assimilation on 2015-03-17T9:00LT

电离层的折射率高度分布依赖于电子密度这一关键的环境参量，同时电子密度剖面可以有效地描述电离层垂直结构的细节。为了验证三维同化模型数据同化的效果，选取处于同化区域内的北京昌平站的电离层测高仪SAO格式观测数据对同化前后的电子密度剖面进行对比，SAO观测数据来自空间环境地基综合监测网。Digisonde系列数字测高仪内嵌的软件，可自动度量标定电离图得到电离层特征参数和电子密度剖面，生成SAO数据[18]。图5给出了北京昌平站上空的电子密度剖面对比结果，可以直观地看出，在大多数时刻同化后的电子密度剖面与真实的观测值更为接近，电子密度峰值与测高仪探测结果相差更小，说明同化算法可以有效地把TEC观测数据融合到背景场，改善提升背景场的数据精度。

图5 2015-12-01北京昌平站上空的电子密度剖面同化结果对比Fig.5 Comparison of electron density profile assimilation results above Changping station, Beijing on 2015-12-01

2.2 电波折射误差修正效果比较

为了验证本文提出的利用空间格点化栅格获取电波射线路径上折射率剖面以及结合IRI模型数据同化进行电波折射误差修正的效果，选取某台工作于P波段的雷达在年积日（day of year, DOY）分别为71、72、73对高轨道卫星目标的三次跟踪实测记录作为实验数据，目标在雷达跟踪视野范围内仰角历经了从大到小的变化，俯仰范围为4°~80°，南北跨越纬度约23°，东西跨越经度约42°。使用GPS精密轨道数据作为测量基准来确定和比较不同方法对各种距离仰角条件下目标的折射误差修正精度。

本文利用射线描迹法对比三种电离层折射率剖面构建方法对修正结果的影响：1）垂直剖面法，即通过IRI模型构建的水平均匀的电离层折射率剖面；2）射线路径剖面法，即通过IRI模型构建的随传播路径变化的水平不均匀的电离层折射率剖面；3）数据同化法，即利用电离层同化现报模型构建的电离层折射率剖面。基于以上的折射率剖面，利用射线描迹法可以计算得到折射误差修正量和剩余残差，雷达测距测角误差分别为雷达探测视在距离和视在仰角与对应目标精密轨道值之差，剩余残差为经修正后的测距测角误差。

图6～8分别给出了三次观测跟踪中三种不同方法应用于折射误差修正中对距离误差修正的表现。可以看出，随着观测仰角降低，三种方法计算的误差修正量均随之增大，在低仰角处基于模型数据同化获取射线路径剖面计算得到的距离折射误差修正量与雷达测距折射误差有更好的一致性，相应地，修正残差结果（子图b）显示利用数据同化法进行距离折射误差修正的残差明显更小，并且修正残差伴随观测仰角变化的趋势更加平缓，很大程度上消除了观测仰角的影响，表明了数据同化方法的有效性。

图6 DOY=71时三种方法距离折射误差修正结果Fig.6 Correction results of distance refraction error by 3 methods when DOY=71

图7 DOY=72时三种方法距离折射误差修正结果Fig.7 Correction results of distance refraction error by 3 methods when DOY=72

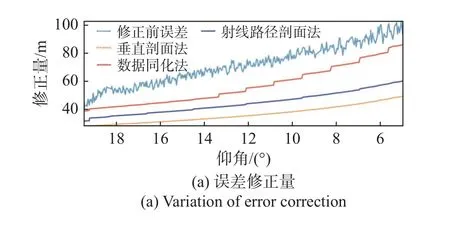
图8 DOY=73时三种方法距离折射误差修正结果Fig.8 Correction results of distance refraction error by 3 methods when DOY=73

图9～11分别给出了三次观测跟踪中三种不同方法应用于折射误差修正中对仰角误差修正的表现。其低仰角情况下误差更为显著的结论对于仰角误差而言仍然成立，最大仰角误差可达0.4°。对比三种方法在仰角误差修正中的差别可以发现，三种方法的修正结果依然是数据同化法更优秀，射线路径剖面法次之，垂直剖面法最差，但是不同于距离误差，三种方法对于仰角误差的修正效果差距并没有那么明显，或者说数据同化方法对仰角误差的修正相对于其他两种方法效果并不显著，这个问题还有待更深入的研究。

图9 DO Y=71时三种方法仰角折射误差修正结果Fig.9 Correction results of elevation angle refraction error by 3 methods when DOY=71

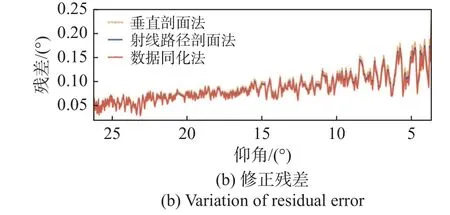
图10 DOY=72时三种方法仰角折射误差修正结果Fig.10 Correction results of elevation angle refraction error by 3 methods when DOY=72

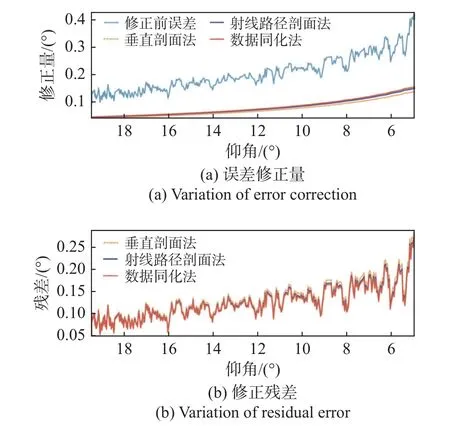
图11 DOY=73时三种方法仰角折射误差修正结果Fig.11 Correction results of elevation angle refraction error by 3 methods when DOY=73

为了量化对比三种方法的修正结果，对利用上述三种方法进行雷达电波折射误差修正的残差进行统计分析，结果见表1、2。其中，数据同化方法距离折射误差修正平均残差分别为15.43、16.97、13.64 m，相比于未进行同化的射线路径剖面方法的修正精度提升了41.2%、35.5%、44.6%，这表明，在三次雷达观测修正中，通过数据同化方法进行电波折射误差修正能极大地提高修正精度。同时，数据同化法的修正结果均方根误差(root mean square error,RMSE)也最小，这表明修正后的残差更为“平坦”，也正如前文所说，对于低仰角的误差修正得到了很大改善。而对于仰角误差而言，如表2，其提升结果有限。

表1 不同修正方法距离折射误差修正残差统计分析Tab.1 Statistical analysis of the correction residuals of distance refraction error

表2 不同修正方法仰角折射误差修正残差统计分析Tab.2 Statistical analysis of the correction residuals of elevation refraction error

3 结 论

本文针对传统折射误差修正方法忽略大气水平不均匀性而采用测站单点位置垂直方向的折射率剖面进行电波折射误差修正的局限性，提出了空间格点化大气和电离层模型同时结合数据同化获取电波射线路径上电子密度剖面的方法。基于某台P波段雷达的外场实测数据和精密轨道数据对三种方法应用于折射误差修正的精度进行了比较分析，实验结果表明，通过空间格点化获取射线路径上的折射率剖面来进行电波折射误差修正相比于利用大气和电离层模型直接获取测站单点的折射率剖面来进行修正有一定的改善，但仍有较大的修正剩余误差，难以满足工程应用中的精度需求。基于空间格点化大气和电离层模型结合数据同化的方法可以有效地增强电离层电子密度分布的准确性，并显著降低雷达测距测角的折射误差修正残差。研究结果验证了利用大气和电离层模型数据同化方法提升电波折射误差修正精度是一个可靠有效的途径。