改进CLR的预测算法在铁路机车牵引系统故障维修中的应用

李 曼，宾紫嫣，周鑫燚，，覃思瑶

(1.北京交通大学 轨道交通控制与安全国家重点实验室，北京 100044；2.北京交通大学交通运输学院，北京 100044)

0 引言

铁路机车设备质量安全状态决定了铁路运输生产的安全状态[1]。当前铁路相关部门积累了大量的“沉睡”故障数据，具有设备数据数量多、种类杂、关联性强等特点[2]。以机车牵引系统为例，随着系统数据采集时效及数据质量不断提高，对数据驱动的故障预测技术的应用需求亟待提升。作为牵引系统中负责电能调节的重要部件，牵引变压器的运行状态对整个系统的安全和稳定性具有重要影响[3]，对牵引变压器的故障预测能够及时发现潜在的故障，为维修方式的选择提供理论支撑。

国内外学者对故障预测进行了大量研究，提出了众多故障预测的模型[4-6]和方法[7-8]。其中多为对特征数据的数学分析，如Nazarizadeh等[9]利用历史数据使用不同的概率分布来分析和预测故障；汪亚平[10]采用累积损伤理论和神经网络模式进行寿命预测与诊断，并根据信息融合和模糊处理对机车故障进行综合分析与诊断等。通常一个系统表现的故障现象往往与多种故障类型的影响密不可分[11]，而聚类算法能够挖掘故障实例与实例之间的关联关系获得各故障类型的特定特征。Wang 等[12]利用聚类算法实现了对监测轴承寿命的自适应预测。k-means是聚类算法中最经典且使用最为广泛的一种基于划分的聚类算法，改进方向与应用广泛[13-14]。研究选择采用k-means 构建故障实例与多种故障类型之间的联系。

目前校准标签排名(Calibrated Label Ranking，CLR)等传统多标签分类方法大部分仍处于理论研究阶段，实际应用阶段的方法多集中于文本分类[15]、图像识别[16]等领域。多标签方法的适用范围较为局限，适用多标签分类方法的数据通常较为复杂[17]，数据的标签体系内结构繁琐。研究基于上述多标签分类方法，在故障预测方面提出一种改进CLR 的预测算法，应用于铁路机车牵引系统故障维修。

研究组织架构如下：第一部分是模型的配置，包括数据处理、模型及评价指标体系的构建；第二部分利用已知数据进行算例验证；第三部分对模型使用效果进行讨论与总结。

1 模型配置

研究将故障数据预处理成可输入算法的故障类型和特征值矩阵及相关矩阵。随后计算自适应正负实例集得到的聚类簇数，对正负实例集利用k-means算法进行聚类[18]；以聚类结果所体现的故障类型特征和实例与故障类型的对应相关关系构建二元分类训练集；根据设备表现比对构建未知实例向量，并通过投票法对故障类型的可能结果进行预测排序；引入一个虚拟校准标签，作为可能性高低的阈值函数更新投票结果[19]，最终预测得到可能相关故障类型及维修方式。算法模型流程图如图1所示。

图1 算法模型流程图Fig.1 Algorithm model flowchart

1.1 自适应设置聚类簇数并聚类

铁路机车牵引系统包含主变压器、牵引变流器和驱动单元等组成部分，其中主变压器结构较为复杂，工作环境负荷较高。目前主变压器的监测项点对设备性能覆盖较为全面，包含温度、油质、气体、阻抗等多种监测对象，能够较为充分地描述各类型故障的特征[20]，因此研究的实验部分选择牵引主变压器作为牵引系统的典型部件进行分析。

根据其系统结构及故障类型对历史数据进行整理，将输入数据确定为2 个矩阵的形式，预处理数据的采集端配置如图2所示。

图2 预处理数据的采集端配置Fig.2 Collection end configuration of preprocessed data

研究以每一次故障数据为实例，每项故障类型为标签，故障类型包括主变压器冷凝器漏油、主变压器冷却风机异音、主变通风机固定螺栓减震器橡胶垫老化等；故障类型对应的具体参数为特征值，其中包含击穿电压、振动频率等具体数值。构建实例与特征值之间的特征矩阵F及实例与故障类型标签之间的相关矩阵R。

式中：m表示所有的实例数；n表示所有的特征数；q表示所有的标签数；aij(1 ≤i≤m，1 ≤j≤n)为该实例的具体该特征参数，如击穿电压、振动频率等；bij(1 ≤i≤m，1 ≤j≤q)为-1 或1，-1 表示该实例不具有对应标签，1 表示该实例具有对应标签，即实例是否在后续维修中诊断出该项故障。

根据相关矩阵R中实例与故障类型的相关性，将实例集合分为每个故障类型标签对应的正实例集合P和负实例集合N。为记录各正负实例集中各故障类型包含的变化信息量，对各标签对应的正负实例集合分别计算标签熵E(k)p，E(k)n。

式中：hp(j)表示在该标签对应的正实例集中，出现的第j个标签向量与在正实例集中出现的总标签向量的比值；hn(j)则对应表示第k个标签的负实例集对应的向量比值。

利用正负实例集的标签熵可计算每个标签的基本熵以评估标签的最小变化。

式中：minE(k)表示该标签对应的正负实例集标签熵中的最小值；wk表示第k个标签的基本熵。

由此计算比率参数rk为

式中：s为平滑参数，此处被设置为1，使之为拉普拉斯平滑。

通过以上参数计算可得到根据训练数据自适应的聚类簇数为

式中：ck表示第k个标签正负实例集的对应聚类簇数；|P|和|N|分别表示正负实例集的基数。对各标签对应正负实例集合以相同的聚类簇数ck分别执行k-means 聚类。聚类结果能够反映实例间的关系和故障类型的深层特性，而聚类中心是对聚类结果的直观体现，根据聚类结果构建映射

式中：ε(x)k表示实例与第j个标签对应聚类结果构建的映射；，，…，为实例与该标签正实例集各聚类中心的欧氏距离；，，…，对应负实例集。

1.2 随机森林二元分类

随机森林是机器学习中的一种常用算法，其基本组成单元为决策树。随机森林法有放回的随机选取数据集中的部分样本，从每个样本的特征中随机选择部分特征，在部分特征中再选择出最佳分割特征作为节点创建决策树，以学到整体数据集的特征。重复选取步骤构建多个决策树形成随机森林，最终通过投票得到预测结果。

1.3 二元投票预测排序

以实例与标签间的相关矩阵和实例映射结果为基础，构建一个二元训练集Djk，该训练集中包含每两对标签间与实例的相关性对应关系。

式中：Djk表示对于每个实例特征向量xi与第j个标签和第k个标签的相关性二进制训练集；Ψ(Yi，lj，lk)表示实例xi相对于标签对的偏好值。对于每个实例对应的训练集，可以利用二进制学习算法B诱导得到一个二进制分类器，即gjk←B(Djk)。依此可由二进制分类器分类结果得到未知实例xu每个可能的类标签的总体投票，票数越高表示故障类型的可能性概率越高。

式中：f(xu，lj)表示未知实例xu可能的类标签lj的投票结果；表示二进制训练集Dkj对应的学习结果投票，若gkj(xu)≤0 成立，则为1，否则为0。当票数相同时，可以被任意打破即随机排名。

在成对比较的框架内，以排好序的标签集为基础，加入一个虚拟标签lv作为高可能性故障类型和低可能性故障类型之间的分割点，其对应的二进制训练集可构造如下。

式中：Djv表示对于每个实例xi与第j个标签和校准标签的相关性二进制训练集；Φ(Yi，lj，lv)表示实例xi相对于第j个标签的相关值。

对于每个新的训练集，得到二进制分类器：gjv←B(Djv)。依据该二进制分类器分类学习结果，对公式⑿中标签lj的总体投票结果进行更新如下。

投票法不会直接输出标签的概率，但通过对标签进行排序，可以得到标签的相对概率分布。根据上述投票结果，未知实例xu的对应相关标签集预测结果如下，即高发生可能性故障类型的合集为

1.4 评价指标体系

研究评价指标体系的建立参考经典多标签分类评价指标[19]。

（1）汉明损失(Hamming Loss)。汉明损失hammingloss用于评价标签被预测错误的频率，记录相关标签被错误预测为不相关及不相关标签被错误预测为相关的标签。

式中：p表示实例数；q为标签数；h(xi)表示实例xi对应被预测错误的标签数。

（2）秩损失(Ranking Loss)。秩损失rankingloss评估反向排序标签对的比例，记录相关标签的预测排名低于不相关标签预测排名的实例比例。

式中：l’表示第i个实例的实际相关标签；l”表示该实例的实际不相关标签；为实例的不相关标签集；f(x，y)为实值函数，表示y是x的相关标签的置信度，由分类学习系统获得。

（3）单个损失(One Error)。单个损失用于评价排名最高的标签与实例不相关的实例的比例。

式中：oneerror是标签的单个损失值；argmaxl∈y f(xi，l)表示实例xi相关排名最高的标签。

（4）覆盖率(Coverage)。覆盖率coverage评价平均需要多少步骤才能向下移动排名标签列表，以涵盖实例的所有相关标签。

式中：rankf是与实值函数f对应的秩函数。

（5）平均精度(Average Precision)。平均精度avgprec用于评价排名高于特定标签的相关标签的平均比例。

式中：rankf(xi，l)为实值函数对应的秩函数，表示未知实例xi预测结果中标签l的排名；rankf(xi，l’)同理。

2 算例验证

主变压器结构复杂，其监测项点对设备性能覆盖较全面，能够充分描述各种故障的特征。本研究方法可适用牵引系统其他部件，这里选择牵引主变压器作为典型部件，进行牵引系统故障分析的算例验证。

2.1 分类器中参数影响

研究在二元分类部分选择随机森林分类器，其中决策树的数量及决策深度、子叶数量对分类结果有着直接影响。根据预测准确度结果，在子叶数量确定为5 的情况下，决策树数量及决策深度对准确度的影响如图3所示。

图3 决策树数量及决策深度对准确度的影响Fig.3 The impact of the number and depth of decision trees on accuracy

由图3 可以看出，当决策树数量100，决策树深度50时，预测准确度最高且稳定性较好。

2.2 聚类簇数的自适应效果

为消除算法在主观选择聚类簇数的影响，研究采用自适应聚类簇数的方法，以第一个标签为例，计算得到的聚类簇数为11。聚类簇数对第一个标签预测准确性的影响如图4所示。

图4 聚类簇数对第一个标签预测准确性的影响Fig.4 Effect of number of clusters on prediction accuracy of the first label

由图4 可知，研究计算的聚类簇数可以有效避免主观选择聚类簇数对预测结果的影响。当聚类簇数设置过小，实例与故障类型的相关性等级划分较宽泛，特征挖掘不够细致；而聚类簇数设置过大时，相关性等级划分过细，对最终的分类结果参考作用不大。自适应设置簇数避免了多分类问题中手动选择各标签聚类簇数对结果准确性、稳定性的影响，验证了改进的有效。

2.3 在大数据集中的改进效果

CLR 是二阶多标签学习转化为标签排序的方法。除了虚拟标签，还以一对一的方式构造标签对的二进制分类器，类不平衡的问题在一定程度上得到缓解，且CLR 的性能在大规模数据集上能有更好的体现。

改进后的CLR 在经典的基础上，考虑标签的底层特定特征，其与标签的直接联系更为紧密，简化了二元分类的难度，改进后评价指标提高显著。由于CLR 算法的性能在较大数据集中有较为明显的体现，而研究所使用的牵引系统数据集因数据较少，不能充分体现CLR 的改进前后特点。因此，采用数据集较大的经典多分类数据集yeast 对比改进前后的性能提升，改进前后CLR 在yeast 数据集中的评价指标如表1所示。

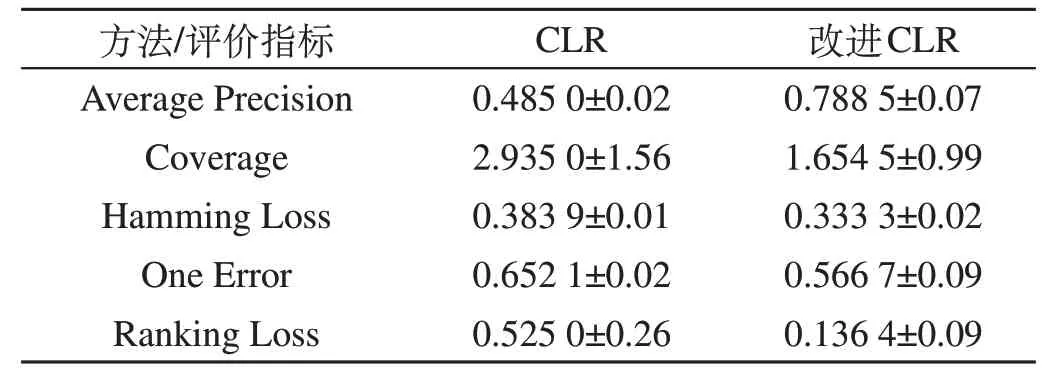
表1 改进前后CLR在yeast数据集中的评价指标Tab.1 Evaluation index of CLR in the yeast dataset before and after improvement

从表1可以看出，改进后的CLR各项指标对比改进前均有不同程度提高，经多次实验，将改进前后各指标的平均指标进行对比，yeast 数据集验证结果如图5 所示，其中覆盖率的指标值已经过归一化处理。

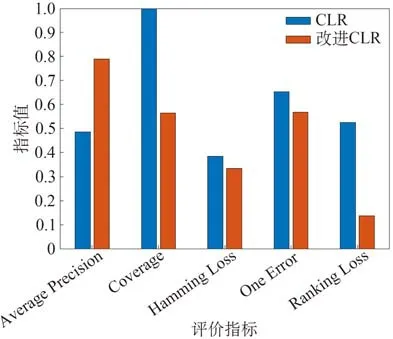
图5 yeast数据集验证结果Fig.5 Yeast dataset validation results

在图5的yeast数据集结果中，相比于经典CLR算法，改进程度最大的秩损失降低了74.0%；其次是覆盖率降低了43.7%；单个损失降低了13.1%，这些指标都与相关标签的预测结果联系紧密，能够有效评估实例的实际相关标签的预测结果。这3 个指标的改进结果说明利用标签对应正负实例集的聚类结果构建映射，能够反映标签的底层特征，使得相关标签的预测准确率及排名结果得到显著提高。平均精度相较于改进前提高了62.6%，汉明损失降低了13.2%，这2 个指标能直接反映未知实例对应的单个标签的预测排名质量和预测准确率，表明聚类结果的应用对分类预测难度的降低有一定影响。

2.4 在实际故障数据集中各类算法的对比

对于铁路机车牵引系统故障数据集，研究随机采用70%的实例作为训练集，30%作为测试集。其中汉明损失、单个误差、覆盖率和秩损失，指标值越小，系统性能越好；平均精度，指标值越大，系统性能越好，最佳值为1。

实际故障数据集与公开数据集yeast 相比，因不同类型的故障易发性程度不一，各故障类型的实例数据量差距较大，即类不平衡问题较严重，导致模型训练的偏差，使得模型更倾向于预测样本数量更多的类别，而忽略样本数量较少的类别。本方法考虑标签之间的相关性和排序关系，从标签相关性的角度缓解标签数量上的类不平衡问题，而不仅是简单地将样本分配给单个类别。最终的标签排序结果，即标签的相对概率分布，可以反映出模型对不同标签的重要性和置信度，从而在一定程度上缓解类不平衡问题。

用实际故障数据集对改进后CLR进行验证，故障数据集改进前后评价指标体系结果如表2所示。

表2 故障数据集改进前后评价指标体系结果Tab.2 Results of evaluation index system before and after improvement of the fault dataset

从表2可以看出，改进后的CLR在各项指标中综合表现较优，相对改进前各指标均有一定幅度的提升，改进程度最大的单个损失降低了78.8%，其次是平均精度相较于改进前提高了31.4%，覆盖率降低了21.7%，秩损失降低了16.7%，汉明损失降低了15.6%。

故障数据集各算法评价指标对比结果如图6所示。

图6 故障数据集各算法评价指标对比结果Fig.6 Results of comparison among evaluation indicators for various algorithms in the fault dataset

在图6中可以发现，改进后的CLR预测算法在牵引系统故障数据集的应用中，相较于其他分类算法，平均精度、覆盖率、单个损失及秩损失的指标中均表现最优，即故障类型的可能性排序质量较高且最有可能的故障类型预测结果准确率较高，可能故障类型的排名都较高。故障类型的可能性排序质量直接影响到维修方式的预测结果，关键故障类型的预测准确率越高，维修方式预测越准确。故障类型排序越高，其故障发生概率越大，准确的可能发生故障类型排序有利于在维修中针对性地予以重视。

以牵引系统部分维修数据为基础进行预测，部分实际故障数据维修预测结果如表3 所示，其中包含对每一维修方式的预测概率及该概率下的预测准确率。预测结果中C4 修的预测数据最多，这是由于实际维修中C4 修属于较常见的小型维修，符合实际修程。根据与数据记录的实际维修内容对比，研究算法的最终预测结果的准确率达96.4%。

表3 部分实际故障数据维修预测结果Tab.3 Prediction results of maintenance for some actual fault data

在铁路机车牵引系统中，击穿电压是采集端最易检测并传输的数据。若检测到击穿电压≥50 kV，预测出C3 修的概率为18.4%、C4 修概率为46.9%、C5 修概率为6.1%、C6 修概率为28.6%。与实际维修记录相对比，当击穿电压≥50 kV时，本方法预测准确率高达98.0%，具有现实指导意义。

混淆矩阵能够反映模型预测结果的真假性比例，归一化后的故障数据集各维修等级混淆矩阵如图7 所示，C3 修与C6 修的预测结果中，真阳性比例较高，预测结果准确性较高，C4 修与C5 修的预测结果中预测失误较多。C5 修为返厂维修等不常见的大型维修，由于C5 修的实例数据占比较低，类不平衡问题仍对结果有一定影响，因此难以区别与C4修特征规律的不同，预测结果稳定性较低。

图7 故障数据集各维修等级混淆矩阵Fig.7 Confusion matrix for various maintenance levels of the fault dataset

尽管改进后在故障数据集上并非所有指标都有明显优势，但综合评价的较优结果表明，聚类结果的应用，使得算法更易得到标签底层特征，能够充分考虑实例与故障类型的相关关系及故障类型间的特征差异，对并发故障类型的排名结果及最终准确度产生积极影响。

3 结束语

改进CLR 在实际故障数据集中预测准确率较高，且并发故障类型的可能性排名质量较高，维修等级预测准确度高达96.4%。该方法在大数据集中改进的效果较为显著，符合实际的铁路部门故障数据预测需求。研究根据经典的CLR 算法，利用正负实例集固定聚类簇数并分别进行聚类分析，将得到的故障类型底层特定特征结合二元分类的训练集，使得结果也更加有效。同时，该方法保留了经典CLR 方法本身在类不平衡问题中的优势，通过考虑两两标签间的相关性得到标签的相对概率分布排序。另外，研究方法在汉明损失方面的改进提高效果不足，相比于更高阶的RAKEL，其结果相差较大。未来将以此为改进方向，在保持其他维度指标效果的同时，提高可能性较低的故障类型的预测准确率。