考虑技术站编组去向的车流径路优化研究

周明玺，郑平标，秦 胜

（1.中国铁道科学研究院 研究生部，北京 100081；2.中国铁道科学研究院集团有限公司运输及经济研究所，北京 100081）

0 引言

在铁路运输中，车流是货流的载体，是兑现铁路货运市场需求的关键因素，也是列车编组计划、货物运输计划、列车运行图编制的基础。国内外有大量的学者对车流径路进行了研究，取得了丰硕的成果。

在国内研究中，基于我国货运需求与路网能力不平衡的事实，车流径路与列车编组计划是密切相关的，其关系被定义为“车流的改编中转站必须限制在车流径路上”和“终点站相同的车流在同一站改编后必须合并为一股车流”[1]。基于车流径路与编组计划的关系，有学者提出“树形径路”的概念以简化车流径路与编组计划在数学上的匹配关系。林柏梁等[2]于2002年提出树形径路配流模型，要求不同发站的车流在某个站汇合后，具有相同到站的车流视作同一股车流，一般不给予拆散。根据这个假设，温旭红等[3-4]引入多商品流理论[5-6]，构建了铁路网车流分配与树形径路综合的混合整数规划问题，并设计拉格朗日松弛算法进行求解。田亚明等[7]分别研究了点-弧模型与弧-路模型在车流径路优化中的应用，指出了点-弧模型适用于精确测算不可行流总量与弧-路模型适用于直观确定不可行OD的特点。高明瑶等[8]根据传统点-弧模型无法直观显示各股车流的最优径路的限制，提出一种改进点-弧的车流径路模型，引入0-1 变量体现车流的实际经由。根据车流的性质，赵娟[9]考虑了不同组织模式下车流径路的优化，刘海涛等[10]考虑多品类车种的车流径路的优化，刘畅[11]在研究中考虑了铁路与其他多种运输方式协作的车流径路优化问题。关于大规模的车流径路优化，Lin 等[12-13]采用基于模拟退火的启发式算法进行求解。Li 等[14]从站-线能力协调使用的角度出发，设计自适应邻域搜索算法进行车流径路模型的求解。

在实际运营中，只有经过相同技术站改编且终点站相同的车流需要进行合并。现有的车流径路模型假设终点站相同的车流在技术站相遇即合并，该假设虽然保证了后续改编车站必定在径路上，但忽略了车流改编的灵活性。当多股终点站相同的车流在某个技术站汇合时，可以选择改编或通过，只有同时选择在该站改编的车流才会合并。

基于此提出一种考虑编组去向的车流径路优化模型。编组去向是指由技术站发出的若干支车流的集合，这些车流以整体的形式进行集结和输送。当具有相同终点站的车流在同车站进行改编时，它们在后续的运输中被视为一股车流。为简单记，假设技术站间编组去向与实际路网的固定径路关联，确定了车流选择的编组去向组合也就确定了车流的实际径路。只有到站相同的车流在相同技术站改编时车流才会合并，此假设规避了车流相遇即合并的限制。

1 考虑技术站编组去向的车流径路优化模型

1.1 问题分析

与典型的网络流问题不同，铁路车流径路优化问题涉及的流具有不可拆分性，在经过技术站改编时，终点相同的车流会进行合并，并在随后运输过程中被视为一股车流。为描述且简化这一特点，学者们提出了一种具有“树形结构”的车流径路优化方案。“树形径路”条件规定了多股终点相同的车流在技术站相遇即合并，然而在实际情况中，可能存在2 股到达相同终点站的车流，其中一股通过技术站，而另一股在技术站进行改编或者2 股车流都通过技术站。在这种情况下，严格遵守“树形径路”条件是不合理的。

铁路车流在路网上并非在相遇时立即合并，而是在经过相同技术站并选择相同去向的情况下进行合并。假设的实际路网拓扑图G2如图1所示，存在技术站3到达技术站1与技术站4到达技术站1的车流，若车流(3，1)选择编组去向方案3→5→1，车流(4，1)选择编组去向方案4→2→1，由技术站编组去向关系组成的网络G1如图2所示，实际车流走行径路如图3 所示，则车流(3，1)的径路为3 →2 →5 →1 如图3 蓝线所示，车流(4，1)的径路为4 →2 →1 如图3 绿线所示。这两股车流经过技术站2后无需进行合并。

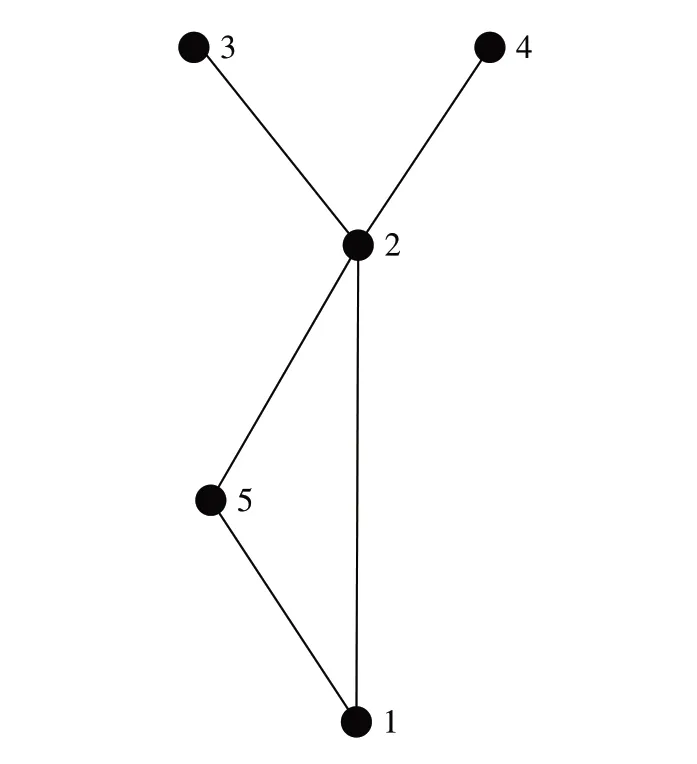
图1 假设的实际路网拓扑图G2Fig.1 Topology map of hypothetical railway network G2

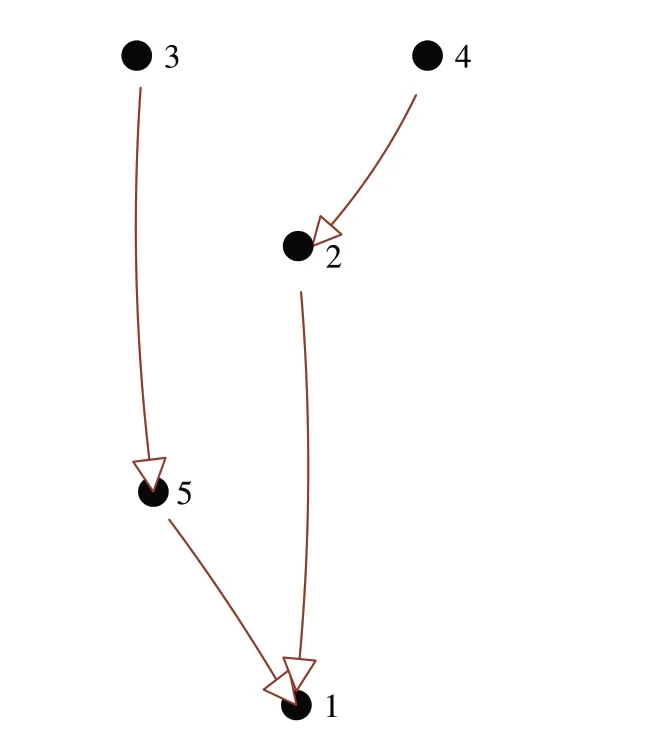
图2 由技术站编组去向关系组成的网络G1Fig.2 Network G1 composed of train destinations of technical stations

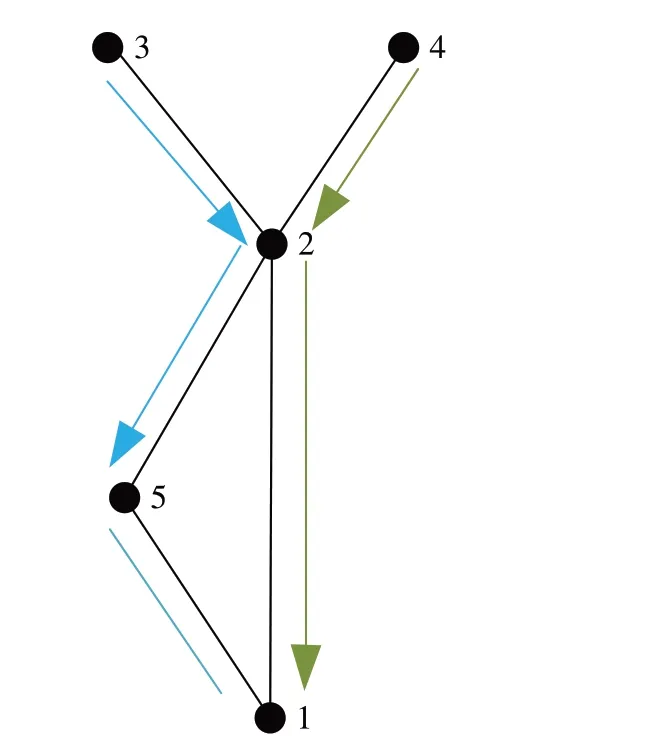
图3 实际车流走行径路图Fig.3 Actual traffic routing map

为了构建基于技术站编组去向的径路优化模型，提出以下假设。

（1）G1=(V1，E1)表示技术站间编组去向网络，V1为路网中技术站集合，E1为连接各技术站的有向弧集合，规定∀i，j∈V1，当车流量一定时，若技术站i能够开行到达技术站j的无改编列车，则有(i，j)∈E1。

（2）每个编组去向(i，j)∈E1与实际路网G2中的一条径路Path(i，j)绑定，为简单记，令Path(i，j)为i，j∈V1间的最短路。

（3）该模型仅考虑了技术站间产生的车流。

1.2 模型构建

对于网络图G1与G2，G1表示由技术站编组去向构成的网络图，G2为反映实际路网中点线连接关系的网络图。在G1中，车流通过选择一系列编组去向(i，j) ∈E1从起点到达终点，编组去向(i，j) ∈E1与路网G2=(V2，E2)中i→j的一条径路Path(i，j)相对应。基于多商品流的建模的思想[4]，构建以车流走行费用最小为目标，满足路网节点流量守恒、区段能力限制、车站改编能力限制以及技术站编组去向的树形径路约束的模型M。模型参数如表1所示。

表1 模型参数Tab.1 Model parameters

模型M如公式⑴所示。

其中，M1与M2均为充分大的正数。

公式⑴为目标函数，表示所定义的车流广义走行费用；公式⑵表示流量守恒约束，表示中间节点的输入流等于输出流，起点和终点流量应等于该点发出流量和到达流量；约束⑶至⑷表示车流不拆散约束；约束⑸表示G2中区段运输能力约束；约束⑹表示技术站改编能力约束；约束⑺至⑻表示G1中的“树形径路”约束。公式⑼至⑾表示决策变量和辅助决策变量的取值范围。

该模型实质是先将车流分配到由编组去向组成的网络G1中，随后基于车流在G1中的选择，提取与之对应在G2上的路径及其相应里程数据。其中，车流在网络G1中需要满足“树形径路”约束、流量守恒约束、车流不拆散约束、技术站改编能力约束，在G2中需要满足区段运输能力约束。车流径路的选择是一个大规模组合优化问题，具有NP-hard 的特性，小规模的问题可以通过求解器进行精确求解，规模较大时需要设计有效算法寻找最优解或满意解，研究设计了一种模拟退火算法进行满意解的搜索。

1.3 模型分解

上述模型中存在难约束⑸和⑹，在执行模拟退火算法程序时，难以生成满足要求的可行解，故考虑将上述约束吸收到目标函数中，新的目标函数如公式⑿所示。

s.t.公式⑵—⑷、公式⑺—⑾

其中，M3，M4为足够大的正数。考虑到在实际作业中，改编次数会对运输组织效率产生负面影响，为简化程序且接近实际，对上述目标函数做以下处理。

定义跃阶函数F(x)如公式⒀所示。同时，为接近实际情况，应尽量减少车流改编次数，以降低改编成本，将具有相同终点的车流在同一站点进行改编操作视为一次改编，车流改编次数K的计算如公式⒁所示。

故将模型M写作以下形式。

综上所述，公式⒂为目标函数，公式⑵—⑷、公式⑺—⑾、公式⒁为约束条件；M3，M4为充分大的正数；M5为较大的正数，用于限制车流的改编次数。

1.4 求解算法

将车流根据终点t∈T进行分类，只有终点相同的车流才有可能进行车流的合并。通过技术站间的连接关系获得图G1的邻接矩阵Z，对于每一类终点属于t∈T的车流，在G1中选择的由编组去向组成的径路满足树形径路约束，故以t∈T为源点，生成图G1的关于源点t的随机生成树，Tree{t}为该树的邻接矩阵，将以t∈T为终点的车流分配到该随机生成树上。当随机生成树确定后，以t∈T为终点的车流在G1上径路也就确定，进一步使得在图G2中对应的径路与走行费用得以明确计算。

令车流(s，t)在Tree{t}的径路为PG1(s，t)，若Tree{t}的边被车流(s，t)的径路PG1(s，t)使用，则矩阵Pst对应元素为1，否则，为0；令矩阵Yst(s∈S，t∈T)对应元素表示G1中各边承载车流(s，t)大小。矩阵X{t}对应元素表示以终点为t的车流分配在G1边的流量大小，其中，s∈S，(i，j)∈E1，故对∀t∈T，有以下公式成立。

Capacity表示在X确定的情况下，路网G2各区间承载流量情况的矩阵，其计算公式如下。

故目标函数可以进一步写成

针对随机生成树的生成算法如下(算法1)，假设输入的有向图为G。

步骤1：转置G的邻接矩阵Z为Z′，此时在Z′中，此时t由终点变为了起点。

步骤2：初始化Tree{t}为零矩阵；H为未被选择点的集合，此时H包含G1中除t的所有点；初始化h为只包含t的集合，用于储存已选择的节点集合。

步骤3：令m是与h中节点相邻的节点集合。

步骤4：剔除m中属于h的节点，若m为空集，进入步骤7。

步骤5：随机选取m中的一个节点mi，并在h中随机选择与mi相连的节点hj，更新Tree{t}矩阵，将hj至mi之间连接关系标记为1。

步骤6：将上述选择的m中的节点加入集合h，在集合H中删除该节点。若H为空，进入步骤7；否则，返回步骤3。

步骤7：将Tree{t}进行转置得到终点为t的关于G1的生成树的邻接矩阵。

模拟退火算法是一种经典的随机搜索类算法，最早由Metropolis提出[15]，该算法具有良好的渐近收敛性，已在理论上被证明是以接近1的概率收敛至全局最优解的优化算法[16]。研究设计模拟退火算法步骤(算法2)，模拟退火算法流程图如图4所示。

图4 模拟退火算法流程图Fig.4 Simulated annealing algorithm flowchart

模拟退火算法最关键步骤是在某一状态下新解的产生，新解的产生方式决定了搜索质量，最坏的搜索方式是通过“全随机”地产生新解，即重复上述可行解生成的环节。这样的搜索效率十分低下，使用模拟退火算法时，通过对当前解施加微小扰动或变换产生新解，保持解之间一定程度的相似性，从而提高搜索效率与质量。为降低搜索的规模，定义车流径路备选集PathG2，PathG2{i，j}用于储存绕行率小于ρ的i→j的实际径路，此处ρ取1.3。为更有效地进行搜索，新解的产生遵循以下步骤(算法3)。

步骤1：随机选取t∈T，并在t对应的起点集合中随机选择一个能到达t的起点s∈S0，其中，记t对应的起点集合为S0⊆S。

步骤2：在车流径路备选集PathG2{s，t}中重新选择一条径路，其中，PathG2{s，t}中所有径路的绕行率低于ρ，记为p2。

步骤3：初始化新的树形矩阵Tree2{t}，尺寸与Tree{t}相同。删除集合S0中的元素s，以排除当前起点的影响。

步骤4：对于S0中的每一个起点，使用Dijkstra算法获取在原始Tree{t}中的各起点到终点t的路径，并在Tree2{t}中保存这些路径，即令对应边的元素为1。

步骤5：处理新径路p2，并对p2中的每一节点执行下列操作：①获取p2(i)在G1中相邻的节点集合A，获取p2中p2(i)之后的节点集合B。②获取集合A与集合B的交集Q，集合Q代表了p2(i)可能存在编组去向的后续节点集。③对于集合Q中的每一节点Q(j)，判断径路Path(p2(i)，Q(j))是否与p2中p2(i)至Q(j)的子路径完全一致。若一致，则在矩阵Tree2{t}中更新p2(i)与Q(j)的连接关系，即对应元素为1。

步骤6：为保证Tree2{t}具备树形结构，调用算法1对Tree2{t}进行处理。

步骤7：将Tree2{t}赋值给Tree{t}，根据公式⒁、公式⒃—⒇更新新解对应的K、X{t}矩阵、Capacity矩阵以及目标函数值。

算法3 的目的是随机选择一股车流，并在尽量不改变其余车流在G1中的径路的情况下，通过调整当前车流在G2中的走行径路，获取该车流及其同属相同终点车流的编组去向方案，从而生成新的X{t}、Tree{t}(t∈T)。这种方法在避免大幅改变整体车流分布的情况下，探索可能的优化空间，寻找更优的车流分配方案。

2 案例分析

2.1 案例介绍

以某地区局部路网作为算例，验证上述模型及算法的有效性。路网结构图G2如图5所示，包括49个技术站，60个区间。

图5 路网结构图G2Fig.5 Railway network G2

假设由编组去向组成的网络G1中相邻车站间存在编组去向，并且每个车站与其隔一个车站的邻近站点间也存在编组去向；代表路网结构的无向图G2中任意区间上下行方向均能通过车流且通过能力相等。设置每个技术站与区间通过能力以及OD流，技术站改编能力如表2 所示，区间通过能力如表3 所示，车流表如表4 所示。

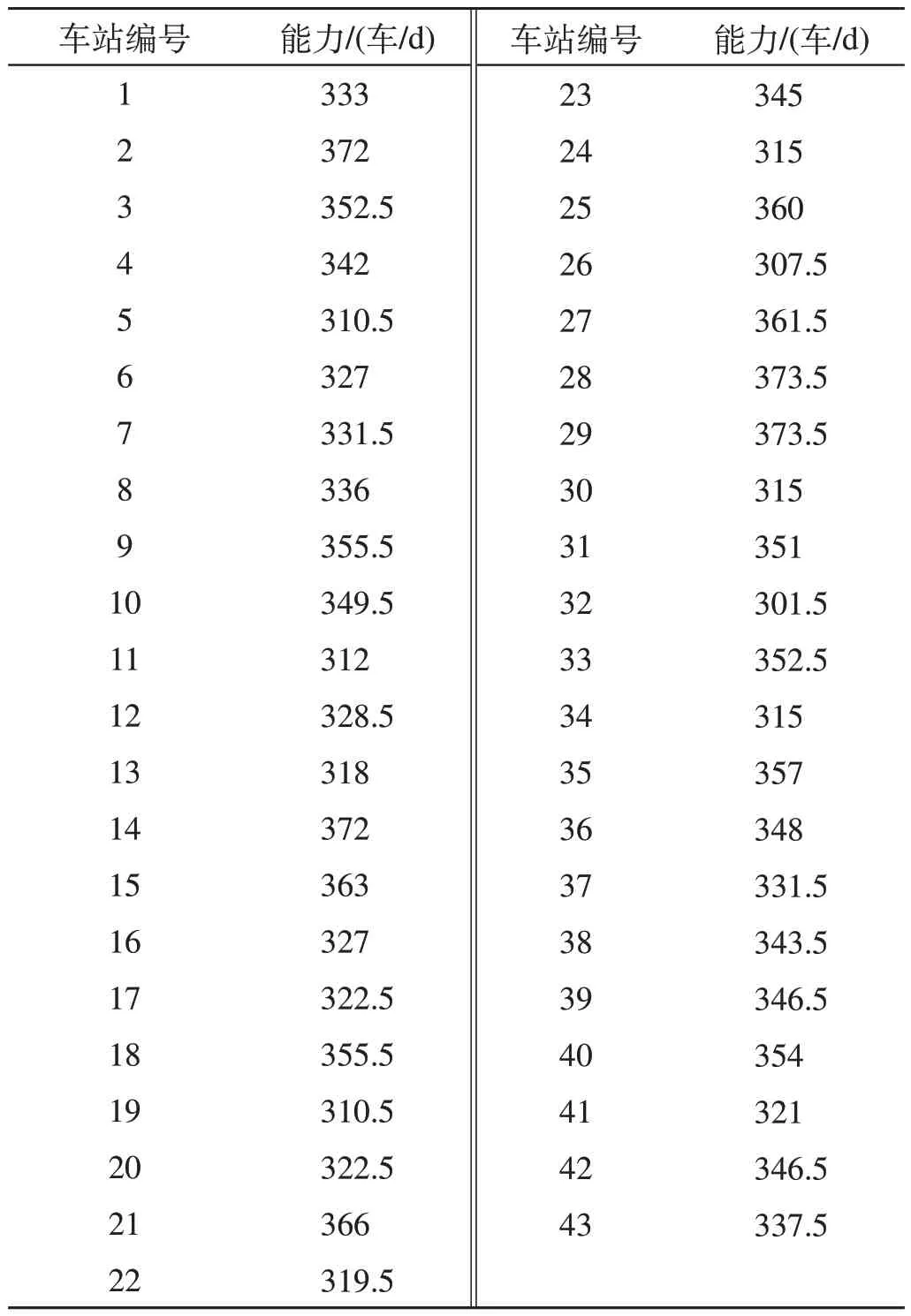
表2 技术站改编能力Tab.2 Formation capacity of the technical stations

表3 区间通过能力Tab.3 Carrying capacity of sections

表4 车流表Tab.4 Table of traffic flows

2.2 结果分析

基于以上数据与假设，在处理器为Intel(R)Core(TM) i9、运行内存为16 G 的计算机上执行上述算法进行求解，初始温度设置为100 000，衰减系数设置为0.9，Markov 链长度为200，为提高求解速度，算法中若同一结果连续出现200 次，则判定为满意解并结束求解。在模型的惩罚函数设定中，惩罚系数M3，M4取100 000，限制改编次数的惩罚系数M5取100。为说明该模型的合理性，本研究将模型的计算结果与文献[4]中提出的包含“车流相遇即合并”条件的车流径路模型的计算结果进行比较。针对文献[4]的假设，为提高计算效率，获得车流径路方案后，路网各车流的编组去向方案根据最远站法则[17]推算，各车站间编组去向关系由G1给出。在此基础上，运用模拟退火算法获得文献[4]的最优解，并将其代入公式⒂中，以计算出广义走行费用。车流径路优化结果对比如表5所示。

表5 车流径路优化结果对比Tab.5 Comparison of the optimized results for the traffic routing

考虑技术站编组去向的适应度进化曲线图如图6 所示，考虑车流相遇即合并的适应度进化曲线图如图7所示。

图6 考虑技术站编组去向的适应度进化曲线图Fig.6 Fitness evolution curve graph considering the train destinations of the technical stations

图7 考虑车流相遇即合并的适应度进化曲线图Fig.7 Fitness evolution curve graph considering the merging of traffic flows upon meeting

图7展示了使用研究设计的算法在文献[4]的数学模型中寻找最优解的迭代过程，纵轴对应目标函数式⒇的值。可以观察到：①在引入技术站编组去向后目标函数式⒇的值有所下降，根据车流相遇即合并的假设的计算结果，有1个车站超过改编容量限制，共计改编93次，出现6条绕行的径路，而根据研究设计的模型，相同条件下，有0 个车站超过改编容量限制，共计改编101次，存在2条绕行径路；②在引入技术站编组去向后，相同终点的车流在经过相同的技术站时，可以根据具体情况选择改编或不改编。这样的灵活性使得车流在径路优化时具备更多的选择空间。

3 结束语

在考虑技术站编组去向的情况下对车流径路进行优化，既符合技术站合并相同去向车流的原则，也增强了车流在径路选择时的灵活性。这一方法的应用避免了传统车流径路优化模型中车流相遇即合并的限制，为车流径路优化提供了更加灵活和切实的解决方案。研究在优化车流径路时，将技术站编组去向考虑在内，通过最短路将编组去向网络与实际路网相联系，构建了一个在编组去向网络中具备树形结构的车流径路优化模型，并设计模拟退火算法进行求解。通过对某地区局部路网的案例分析，与传统的“树形径路”模型相比，研究所提出的模型不仅在目标函数方面表现更优，还引入技术站改编能力限制，加强车流径路与路网能力间的适配。然而，模型仅将最短路径与编组去向绑定，未充分考虑编组去向对应的实际路径，因此与实际应用存在差距。未来的研究方向应当更深入地研究实际路网中技术站间编组去向与车流径路的匹配，以更贴近实际应用的需求。