基于最小间隔法的单线铁路车站分布优化

马 强

（中铁一院集团新疆铁道勘察设计院有限公司 运输经济所，新疆 乌鲁木齐 830011）

0 引言

从近年来新疆铁路建设情况来看，疆内铁路多以单线为主，单线铁路车站分布调整优化问题是单线铁路工程设计过程的重要环节，科学合理的车站设置可最大限度地满足运输需求、节省工程投资、降低运营成本，有助于提升铁路运输竞争力。单线铁路工程设计工作中的铁路车站分布调整优化问题，是指在新建单线铁路设计过程中，根据初步线路方案，结合沿线客货运需求分布中间站，在保证区间通过能力条件下，进一步分布会让站。结合我国现有铁路建设现状，我国新建铁路主要以中间站及会让站(或越行站)车站站址分布为主。

我国单线铁路现行区间通过能力计算法为静态确定性扣除系数法[1-2]，例如伍杰源[3]研究了铁路应用移动闭塞技术后的效率问题，并得出按照扣除系数法计算单线铁路线路通过能力可充分挖掘普速铁路潜力的结论，但这种严格“按图行车”、要求运输工作不中断、设备无故障、列车占用均等等约束条件下所得的最大通过能力，是以牺牲客货运输质量为代价，缺乏灵活性且难以实施。扣除系数法计算结果一般偏大，若作为规划依据，一定程度上会使铁路运输缺乏灵活性，且扣除系数法规定的各类别列车扣除系数为范围取值，但实际工程设计工作中，因具体设计人员取值不同而导致结果存在一定差异。基于此，有学者提出不同能力计算方法。例如张伦等[4]运用国际铁路联盟提出的UIC406 方法计算铁路区间通过能力，并对京津城际铁路区间通过能力进行计算和评价；孙晚华[5]基于我国尚未形成统一干线铁路通过能力计算现状，提出干线铁路通过能力定义，构建了通过能力计算公式及相应求解算法。此外，张超等[6]以铁路枢纽车流量通过能力为约束条件，构建了以铁路枢纽通过能力最大为目标函数的模型并设计元启发式算法进行求解；赵鹏等[7]针对我国部分单线铁路亟需扩能问题，构建了成对追踪运行周期时间最小化的单线铁路通过能力混合整数规划模型，并借助Lingo12完成求解。

铁路通过能力是单线铁路车站分布优化的基础，借鉴既有研究对单线铁路通过能力的研究思路，针对新建单线客货混跑铁路的车站布局问题，采用平均最小列车间隔计算法，以满足客货运输需求和衔接多方向站点需开站为两大紧性约束条件，构建了非线性整数多目标优化模型。

1 铁路车站分布问题分析

1.1 问题描述

记I为双向行车单线铁路(简称“单线铁路”)站点集合，规定单线铁路车站序号依上行方向顺次增大，站点i，j，k∈I；记e为区间，eij为车站i至车站j的区间；记tij为车站i至车站j的区间运行时间，min；记P为单线铁路线路，则eij∪ejk∪…∪emn=P，eij∩ejk∩…∩emn=∅。

1.2 平均最小列车间隔时间

单线铁路区间通过能力平均最小列车间隔时间计算法[8]是以排队论为理论基础，以保证实现一定铁路列车工作质量要求的计算方法，运用此方法铺画的运行图是具有较强应变性、更符合实际工作且可实施的柔性运行图。

为便于后文叙述，将单线铁路最小间隔计算法基本要素做简单说明如下。

（1）区段：具备一定接、发车能力的两车站间铁路地段，由一个或多个区间组成。

（2）区间：以线路所、车站所划分的线路空间地段，其中线路所间或线路所至车站间的线路空间地段称为所间区间，车站间的线路空间地段称为站间区间。

（3）运行列车组：列车运行图上相同或不相同运行方向两相邻列车所组成的列车运行图结构单元，记运行列车组数矩阵为U，对/d。

（4）最小列车间隔时间：运行列车组两列车在同一区间内运行过程不受彼此干扰的最小时间间隔，记最小列车间隔时间矩阵为M，min。

（5）列车种类组：铁路区段内不同种类(按运输任务、旅行速度或运行特征等进行划分)列车归并组合的列车组，记列车种类组集合为A。

1.3 模型构建

1.3.1 目标函数

在单线铁路运输需求已知条件下，针对双向行车单线铁路，考虑铁路工程投资和运营费用支出节省，应在满足客货运输需求基础上，尽可能减少沿线车站开站；另一方面，结合既有研究[9-11]可知，根据线路既有固定设备，在一定类型机车、车辆和一定行车组织方法条件下，应尽量高效利用铁路区间通过能力。开站数量目标函数与通过能力利用率目标函数如公式⑴、公式⑵所示。

式中：n为车站站点总数；xi为0-1决策变量，其值为1表示第i个车站开站，反之则关站。

式中：Cij为区间eij的各类别列车数，对/d；Nij为由平均最小列车间隔时间计算法所获得的区间eij通过能力，对/d，其值计算如公式⑶所示。

1.3.2 约束条件

（1）区间约束条件。单线铁路线路P的区间eij两端衔接车站必须开站，约束表达式如公式⑷所示。

（2）能力约束条件。单线铁路区间能力必须满足客货运输需要能力，约束表达式如公式⑸所示。

由公式⑴至公式⑸可知，研究所构建模型为针对单线铁路的非线性整数多目标规划。

2 模型算法设计

非线性整数规划问题的求解尚未找到通用解法，运用数学精确算法[12-14]目前只能求解特定模型，而采用启发式算法[15-17]求解该问题会体现较大优越性。针对模型特点，运用带精英策略的非支配遗传算法进行求解。算法步骤如下。

步骤1：依铁路线路上行方向对沿线站点顺次编号，确定线路站点集合I。

步骤2：确定染色体编码方式为二进制编码方式，并设定算法参数，相应基因位(即决策变量xi)个数为|I|，算子| ⋅|表示集合元素个数。

步骤3：计算平均最小间隔时间，即：①划分列车种类组，确定集合A；②确定类别运行列车组数矩阵U；③根据列车运行图要素值及其他参数计算平均最小列车间隔时间-----Mij。

步骤4：运用罚函数法确定℘⋅Δ，其中℘为惩罚系数，Δ由公式⑹确定。

从而构建适应度函数如公式⑺所示。

步骤5：令迭代次数t=1进行种群Ft的初始化。

步骤6：运用NSGA-Ⅱ算子得子种群Ct，并将其与Ft合并得集合Ht。

步骤7：对步骤5 所得结果进行非支配排序形成非劣解集；对各层个体进行拥挤度计算，按层级顺序选取Num个染色体构成新一代种群Ft+1。

步骤8：判断t>gen，gen为算法总迭代次数，若成立，算法终止，否则t=t+1，执行步骤6至步骤8。

该算法时间复杂度为O(λ⋅Num⋅Num)，λ为目标函数数量。

3 算例分析

3.1 算例分析设计

3.1.1 算例背景

在实际工程设计中，单线铁路布点以近期经调运量为依据，并考虑储备系数0.2，据此计算需要能力。根据需要能力不大于设计能力的原则，反推最大站间距，结合线路设计坡度，尽量均衡分布单线铁路各个站点[18]。此外，沿线各车站设计需要充分考虑预测运量，有客货运作业的车站必须设置开站，衔接多个方向的站点及有其他特殊要求的站点也需要开站。

以和若铁路(和田—若羌)作为算例。新建和若铁路位于新疆维吾尔自治区和田地区和巴音郭楞蒙古自治州境内。该线从喀和铁路(喀什—和若)的和田车站接轨，经过和田、洛浦、策勒、于田、民丰、且末、若羌等7 个市(县)及新疆生产建设兵团第二师三十七团、三十八团、第十四师二二五团，接入本线终点格库铁路(格尔木—库尔勒)若羌站。线路全长825.00 km；本线在和田地区境内线路长度402.50 km；在巴音郭楞蒙古自治州境内线路长度422.49 km。桥梁总长80 245.4延长米，其中特大桥64 307延长米/21座、大桥7 122延长米/29座，桥梁占全线比例9.73%。全线共设车站69处(不含接轨站和田和若羌)，洛浦、策勒、二二五团、于田、民丰、三十八团、三十七团、且末、瓦石峡共9 个站为中间站，其余60 处车站为会让站或预留会让站。和若铁路为新建单线内燃铁路。新建和若铁路地理位置图如图1所示。

图1 新建和若铁路地理位置图Fig.1 Geographical location map of Hetian-Ruoqiang Railway

和若铁路站点及编号表如表1 所示，除起讫点外只展示9 个主要中间站，全部车站平均站间距11.78 km，最大站间距13.50 km (区间托格日尕至先拜日尕)。

表1 和若铁路站点及编号表Tab.1 Number and station of Hetian-Ruoqiang Railway

研究采用的列车运行图要素如表2所示。

表2 列车运行图要素 minTab.2 Train operating plan element

由牵引电算软件仿真的货物列车平均区间运行时分为11 min，旅客列车平均区间运行时分为9 min，其中货物列车设计速度90 km/h，旅客列车设计速度120 km/h。由于客货运输需要及其他需要，洛浦、策勒、二二五团、于田、民丰、三十八团、三十七团、且末、瓦石峡9 处中间站为必开站，两端接轨站亦为开站。天窗维修时间90 min。和若铁路列车种类组如表3所示。

表3 列车种类组Tab.3 Train category group

按运行列车组前行列车与后行列车所属列车种类组的异同，可将运行列车组分为若干种类的运行列车组，由于仿真算例为新建双向行车单线客货混跑内燃铁路，牵引机型以DF8B为主，表1中任一列车种类组的列车，既可作为运行列车组的第一列车，又可作为运行列车组的第二列车；既可作为列车运行组的上行列车，也可作为运行列车组的下行列车。本算例中运行列车组种类数为36 种。和若铁路运行列车组种类构成矩阵表如表4所示。

表4 和若铁路运行列车组种类构成矩阵表Tab.4 The matrix table of train category groups of Hetian-Ruoqiang Railway

本算例双向行车单线区段运行列车组种类数(以行为准)分别为：6，6，10，10，5，5。根据中国铁路乌鲁木齐局集团有限公司既有运行图资料，列车平均进入晚点时间为12 min，列车进入晚点概率为0.6。算例列车后效晚点时间总值不超过150 min。

3.1.2 染色体设计

按照表1 编号，依和若铁路下行方向顺次编码，染色体编码方式如图2所示。

图2 染色体编码方式Fig.2 Code mode of chromosome

根据模拟二进制交叉算子，从亲代个体中产生子代，染色体交叉方式如图3所示。

图3 染色体交叉方式Fig.3 Cross mode of chromosome

根据多项式变异算子，染色体变异方式如图4所示。

图4 染色体变异方式Fig.4 Mutation mode of chromosome

3.2 算例求解及分析

3.2.1 求解结果

由2.1 节可知，A={A1，A2，A3}，U=(u)9×9，T=1 440 min。相同种类运行列车组概率为0.19，列车占用区间总时间为666.50 min，平均最小列车间隔时间为15.87 min，相同种类运行列车组平均最小列车间隔时间为15.78 min，不同种类运行列车组平均最小列车间隔时间为16.25 min。平均必要列车运行图缓冲时间-----tijrerf为32 min，基于列车最小间隔法的通过能力值为30.08对/d。

基于以上数据，设变异概率prm=0.03，交叉概率prc=0.84，种群规模Num=350，迭代次数gen=600，惩罚系数℘=5 000。算法迭代过程如图5 所示。Pareto分层图如图6所示。

图5 算法迭代过程Fig.5 Iterative process of the algorithm

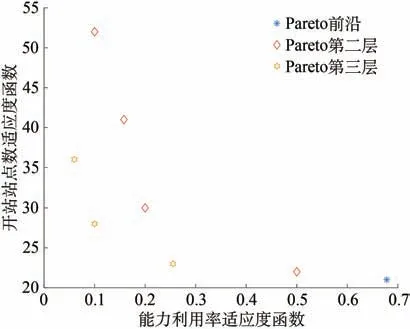
图6 Pareto分层图Fig.6 Pareto hierarchical diagram

由图5、图6可知，该算法在迭代150代左右收敛，算法具有较强稳健性；函数拥挤度较为均匀，分层明显；此外，Pareto 前沿面仅含一个元素，说明该模型具有优化解。

第600代对应算法求解结果如表5所示。

表5 第600代对应算法求解结果Tab.5 The 600th solution results of algorithm

由表5优化结果可知，洛浦、策勒、二二五团、于田、民丰、三十八团、三十七团、且末、瓦石峡等必开站均为1，这些必开站是为提高铁路运输质量，列车进行检修或具备较大客货运量非开不可的站点，即表5 下划线基因位所示；在必开站基础上另开拜什托格拉克、也斯尤勒滚、亚通古孜、托帕克、三十八团、喀拉米兰、西域塔且、阿克吐孜、五苇场、塔什萨依、塔特勒克10 处会让站，这些必开会让站是可以满足研究年度最大需要能力，同时能避免能力虚靡的较优开站点。

3.2.2 结果分析

研究所得结果与按照扣除系数法计算出的开关站分布情况一致，采用本方法并未减少开站数量，其主要原因是：按照研究所提基于最小间隔法获得的区间通过能力约为30对/d，而按照静态扣除系数法计算得到的区间通过能力约为40对/d，本算例区间需要能力约为25对/d，计算所得区间通过能力均大于区间需要能力，故分布情况一致；进一步地，如果考虑必要缓冲时间使基于最小间隔法获得的区间通过能力小于区间需要能力，而由扣除系数法获取的区间通过能力大于区间需要能力，则铁路沿线开站数需要增加。

为了研究最小间隔法各参数取值对计算结果的影响，以晚点概率密度函数参数a，m和平均必要列车运行图缓冲时间-----tijrerf为扰动分析元素，列车后效晚点时间总值不超过150 min，进行参数敏感性扰动分析，参数扰动分析如图7所示。

结合图7 可知，基于列车最小间隔法计算得到的通过能力值与平均必要运行图缓冲时间成反比，而晚点概率密度函数参数a，m会直接影响到该值的取值，三者间的关系存在多极值点，研究取值即为其中一个极值点，该点处的值具有稳定性，使目标优化迭代效率更高，求解结果更满意。

4 结束语

考虑铁路设计人员计算铁路站点分布的效率问题，构建了单线铁路的非线性整数多目标规划模型；根据算例求解结果及效率分析，研究所提方法一方面可替代行车设计人员传统的车站分布手动计算调整过程，显著提高专业设计人员的设计效率，另一方面可为稳健列车运行图的铺画提供一定的参考；获取的铁路车站分布优化结果，根据和若铁路案例验证，与传统工程设计结果一致，具有较高准确度，横向拓展了工程设计车站分布优化内容。但模型中存在未考虑铁路站点内部各设施能力利用情况等不足之处，这是下一步研究的重点。