省域公路货物运价抽样监测方法

赵转转，马廷博，马振祥，王钊龙，闫晟煜

（1.陕西交通职业技术学院 汽车工程学院，陕西 西安 710018；2.中广核铀业发展有限公司核燃料二部，北京 100081；3.长安大学 汽车学院，陕西 西安 710064）

0 引言

2013—2014年交通运输部、国家发展和改革委员会相继印发《关于开展道路货运价格与成本监测试点工作的通知》《关于做好货物运输价格监测工作的通知》等文件，要求组织开展货物运价监测工作，公路货物运价动态监测成为省域道路运输市场常态化监测任务。一直以来，限于货物运价持续变动、企业数量众多、运价结构复杂等因素，省域货物运价监测体系尚不完善，影响到管理主体对运价行情的及时掌握和宏观运力调控。公路货物运价为市场调节价，道路货物运输每周运价持续波动，省域内各货运企业报价互有差别[1]，一般通过建立运价指数按月监测。中国物流与采购联合会在2012年公布了全国货物运价指数[2]，考虑了经济环境、政策导向、柴油价格、人工成本、货物行情等因素，为研判货物运价态势提供了有力的分析工具。由于各省经济区位、资源分布存在显著差异性，省域货物运价规律与全国总体规律不尽一致，也需及时掌握运价变化动向。与此同时，铁路历经2013 年之后的2 次货运改革，在长运距“白货”的运能方面持续发力[3]，建立中国铁路95306 货运平台，借助运价低的优势，公路长运距货运受到一定冲击。近年来柴油油价持续走高，增加了运输成本，拉大了公路与铁路运价的差距，一些时效性不强的普通货物纷纷由公路运输转向铁路运输，影响到公路运力的总体调控。多种因素影响下，有必要建立一套省域公路运价抽样监测体系，用于调控货运市场、精准施行政策和运价及时反馈等工作的有序开展。

有关货物运价的既有研究多从运价指数、定价模型、运价预测、运价调整机制和公铁运价对比等方面展开。运价指数及运价模型多建立在自回归移动平均(ARIMA)模型、评定(Logit)模型、斯塔克伯格(Stackelberg)模型、自回归条件异方差(ARCH)类模型和拉式方法等基础上。2015年以来，一些省份也在逐步建立省域公路货物运价监测体系，监测领域集中在生鲜冷藏运输、煤炭运输、原油与成品油运输和集装箱运输等。货物运价研究方面，原云霄等[4]采用ARIMA 模型预测我国公路运价指数，运用数学软件和月度数据验证模型合理性；周茵等[5]基于总体、分类和个体指数提出铁路货运价格指数体系；肖本佳等[6]运用指数编制理论建立运价指数算法；来浩楠[7]运用煤炭市场大数据编制煤炭公路运输价格指数；Shackman等[8]运用向量误差校正模型，检验海运、铁路、公路和航空货运费率的协整关系；Kyriakou 等[9]基于运价指数回归模型为货运期权开发精准估值方法；Duru 等[10]提出用于干散货运输的长期航运运价指数；张双霞等[11]构建基于ARIMA模型和支持向量机(SVM)模型的公路运价预测模型；赵福杰等[12]建立铁矿石运价的自回归移动平均(ARMA)与霍尔特-温特斯方法(Holt-Winters)非季节组合模型；张若梦等[13]依托运价数据计算全局和局部莫兰(Moran)统计量，建立带有空间滞后项的空间自相关模型，分析货物运价的影响因素和空间效应；Chen 等[14]采用多重分形技术，分析了波罗的海地区干散货的运价指数；Parumog 等[15]基于汽车燃料价格变动因子提出公路运输定价的总体结构；Gohari等[16]解析运输燃料价格上涨对集装箱运输成本的影响；Macharis等[17]基于比利时多式联运码头区位分析(LAMBIT)模型研究燃料价格上涨10%时对货运增长的促进作用。

目前各省对公路货物运价的分析角度互有不同，采取手段较为灵活，如按整车、零担轻货、零担重货和集装箱运输来分类。一些省域公路运价监测以典型企业报送的运价作为基数发布，然而少量的监测样本对运价精度和分析质量有一定影响，也鲜见在抽取样本时考虑省域地市分布情况。鉴于此，研究提出一种公路货物运价抽样检测方法，满足运价推算精度，并通过省域数据验证方法的可行性，以期服务于公路货物运输行业的动态监测任务，实现高效率、低成本的货物运价动态信息实时掌握。

1 运价监测体系架构

1.1 抽样监测流程

省域内各地市货物运价以企业为依托采集数据，企业是关键的调查对象。货运企业按照拥有车辆数不同，分为规上企业、规下企业。规上企业分为拥有车辆数100辆以上企业、50～99辆企业，共2个层级；规下企业分为拥有车辆数10～49辆企业、5～9辆企业和4辆及以下企业，共3个层级。规下企业不如规上企业经营稳定，对货物运价的报价存在变动幅度偏大的特点，因而规上企业更适合作为调查对象。

道路货物运输企业经营范围分为普通货物运输、货物专用运输、大型物件运输和危险品货物运输，其中各省域普通货物运输计价方式有一定通用性且运输量比例最大，根据2019 年道路货物运输量专项调查结果，一些省份甚至达到92%以上，是公路货物运价动态监测的关键，而普通货物运输又分为整车运输、零担轻货运输、零担重货运输和集装箱运输4 种报价类别。普通货物运价因报价类别、运输线路、承运货物品类等不同而不同，货物运价抽样监测体系流程如图1所示。

图1 货物运价抽样监测体系流程Fig.1 Process of freight rate sampling monitoring system

货物运价抽样过程根据全国经济普查每5 年执行1 次，当样本不适应监测要求时可通过样本轮换解决。货物运价与货物品类关联密切，不同货物品类报价类别不同，运价算法也不同；运输距离也对运价有影响，公路运价算法在400 km以内与800 km以上存在显著的差异性。因此，样本分配阶段应充分考虑省域内运输的货物品类比例构成、运输线路分配问题。

1.2 分层抽样理论

获取省域各地市内规上企业的总体数，采用分层抽样法计算样本数。通过分层可增大各属性中的共性，易于抽出具有代表性的调查样本。因此，将总体按其属性分成若干层，在各层中随机抽取样本单位调查。对于给定的置信水平，总体方差越大，需要的样本量就越大。若总体是由几个差异明显的独立部分组成，且总体与样本之间存在一定的一致性时，分层抽样法中每层的方差要小于总体方差，样本容量较不分层抽样的方法大幅减少，可提升工作效率。根据分层抽样最优分配原理[18]，估计最低样本容量为

式中：n为最低样本量；Wh为第h层总体层权；为总体第h层方差；V为估计量方差；N为总体量。

式中：Nh为第h层总体量。

式中：d为抽样绝对误差；t为标准正态分布的双侧分位数；r为抽样相对误差，控制在5%～10%；Yˉ为总体均值。

奈曼分配为

式中：wh为第h层样本层权；nh为第h层样本量。

标准正态分布的双侧分位数可由常用分位数表查询得到，95%置信区间为1.96，90%置信区间为1.65。运用公式时先计算地市平均值，再计算该地市层内方差，结合该层层权和估计量误差，计算最低样本量，抽样分为2 层，第1 层为省域地市层，第2 层为规上企业层。根据规上企业层内标准差，可控制置信区间为90%～95%。

2 样本分配与数据报送

交通运输行业标准《运输货物分类和代码》(JT/T 19—2001)将货物分为17种品类，根据省域每5 年1 次的货运专项调查获得各地市普通货物品类的运量比例βi(i=1，2，…，17)[19]。按照各地市的βi拆分企业样本n0，可表示为

结果按照四舍五入计，每个企业重点监控3～6种货物品类。当规上企业缺少某货物品类的企业时，可在下一层的规下企业中寻求样本调换。

零担轻货按照货物包装最大外廓尺寸计算体积，按333 kg/m3计算其计费质量；零担重货对货物的划分界限为运载因数小于1.132 8 m3/t或40 ft3/t的运输。不同货物品类的报价类别如图2所示。

图2 不同货物品类的报价类别Fig.2 Quotation category corresponding to goods category

石油、天然气及制品和化工原料及制品多属于危险品运输，不在普通货物范畴内[20]。样本分配过程不区分企业层级，按照所属的重点监控货物品类报送运价，典型运输线路一般含市内线路、省内线路、省际线路，企业根据运输距离自行确定典型运输线路。每种重点监控货物品类的运价报送内容如表1所示。

表1 每种重点监控货物品类的运价报送内容Tab.1 The freight rate submission content of each priority goods category for monitoring

一些货物虽然以整车形式运输，如煤炭、金属矿石等，但可采用零担重货形式报价，报价类别灵活多变，运价数据采集时可确定唯一报价类别执行。报价数据接收后，对分析异常数据予以核实验证，可运用Z-分数筛选月度报价异常数据。

式中：Z为报价X的分数值；E为报价X的平均值；σ为报价X的标准差。

货物运价变量X具有正态分布特征，引入拉依达准则(3σ准则)判断异常运价数据，即当Z∈(-3，3)时认为X为正常数据，当Z超过阈值边界则认为X为异常数据。

省域规上企业常与上游生产企业签订年度货运承包合同来锁定整批货源，而零散的货物主要通过规下企业和个体户运输完成。无车承运人平台近年兴起，其运单数据中含有大量的实时运价信息，涉及整车、零担轻货、零担重货、集装箱、冷链运输和大件运输等多种道路货运报价类别，是理想的货物运价数据源，也是货物运价动态监测的有效补充[21]。然而，无车承运人运价数据并不能完全代表省域运价，缺少全局运价特征，如合同制货物运价等。

3 案例分析

2019 年某省开展普通货物运价抽样监测工作，提取9 月道路运政管理信息系统中各地市的规上企业数，按照分层抽样理论计算抽样样本数，取抽样置信度为90%，r=0.1，t=1.65，车辆数分别为100辆以上企业、50～99 辆企业的抽样结果。规上企业抽样数计算结果如表2所示。

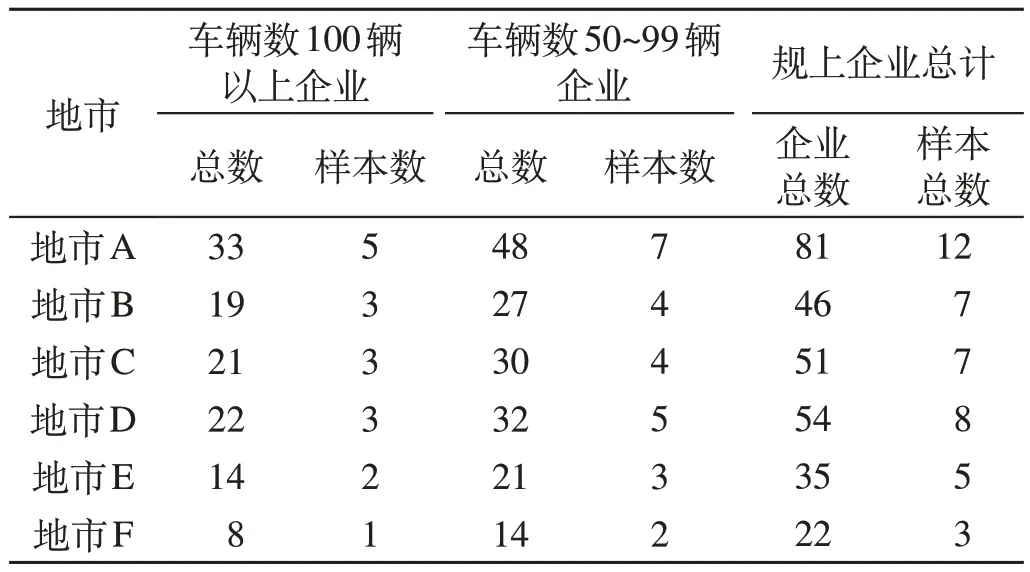
表2 规上企业抽样数计算结果 个Tab.2 Results of samples of enterprises above the designated size

初步计算得到总抽样企业数为42 个，总体抽样比例为14.49%。计算过程中发现，每个地市内车辆数为100 辆以上与车辆数为50～99 辆的企业数量差距(即二者标准差)越小，总体抽样比例则越小。此外，地市F的样本总数不足以覆盖行业标准中的17 种货物品类，需要在地市F 车辆数为10～49 辆的规下企业中降档选取2 个企业补充，因而总抽样企业数为44个。

提取2019年9月各地市货物运输量专项调查中普通货物品类的运量比例βi，按照公式⑸，拆分表2中规上企业样本总数。以地市A、地市B 为例，抽取企业样本对货物品类覆盖情况。地市A 和地市B的规上企业覆盖货物品类拆分如表3所示。

表3 地市A和地市B的规上企业覆盖货物品类拆分Tab.3 Splitting of goods categories covered by enterprises above the designated size in city A and city B

表3 中地市A、地市B 覆盖的货物品类未达到100%覆盖，这是由于非危险品运输的石油及天然气制品、化工原料及制品等2 种货物品类很低，地市A、地市B分别为5.88%，7.69%，而且总体货物品类覆盖的置信度已超过90%，因而统计中忽略这2 种货物品类的影响。表3 中企业样本数的拆分比例与覆盖货物品类基本一致，符合企业样本总数拆分规律。

被抽样的企业按照表1 填报指定监测货物品类的运价，定期报送，通过在线共享文档汇总数据，采取按照样本量对不同货物品类运价加权的方式，可得到不同运输距离下的整车、零担轻货、零担重货和集装箱运价。例如，以2019 年各报价类别为基价，按照400 km 以内、400～800 km、800～2 000 km的3种运输距离，整理部分2021年货物运价波动情况。不同报价类别下的运价月度波动情况如图3所示。

图3 不同报价类别下的运价月度波动情况Fig.3 Monthly fluctuation of freight rates under different quotation categories

由图3 可知，整车、零担轻货和零担重货运价在2021 年内基本呈现一季度偏低、二季度趋稳和三、四季度逐步提升的态势；春节过后，3～4 月不同运输距离的运价指数基本达成一致，而到7 月后又出现不同运输距离运价分化的状况；该省份3 种报价类别在1～2 月春节期间差异性显著。图3 中货物运价体现了该省货物运价的整体走势，也同时验证了货物运价抽样方法、按照货物品类分配企业样本和异常报价数据筛选等处理环节具有良好的可行性和稳定性。

4 结束语

（1）通过剖析货运企业分类和经营范围，运用分层抽样理论，提出普通货物运价抽样监测体系，引入企业承运的货物品类比例拆分抽样样本，按照运输距离和报价类别采集货物运价数据，利用Z-分数和拉依达准则建立审核标准来筛选异常报价数据，当规上企业不足以覆盖所有货物品类时，提出采用拥有车辆数为10～49 辆的规下企业补充监测样本缺失的方法。

（2）运用实例省份数据验证货物运价抽样监测方法的可行性和稳定性，抽样监测方法的置信度可达90%以上，研究发现每个地市内车辆数为100辆以上与车辆数为50～99 辆的企业数标准差越小则总体抽样比例越小的规律。

（3）货物运价构成复杂，货物专用运输和危险品运输的运价划分由于定价规则具有高度市场化的特点，研究仅探讨普通货物运价监测，而未详细阐述其他经营范围的货物运价监测方法；在下一步研究中，将重点探索危险品运输、冷链运输和特种货物运输的运价监测问题和省域内通用运价指数模型构建问题。