如何让学生理解“长方体体积=底面积×高”
周桂芬
学生对“长方体体积=底面积×高”的理解,往往局限于“下底面的面积×高”这一思维定式。为了帮助学生突破这一思维定式,深入理解该公式的本质,可以实施以下教学过程。
一、问题驱动,引发思考
1.呈现问题,引发冲突
出示题目:一根长方体木料,长5分米,横截面的面积是3 平方分米(如图1),这根木料的体积是多少?

图1
教师提问:“长方体体积=长×宽×高,现在只知道长方体的长和横截面的面积,该如何计算长方体的体积?”
2.独立思考,猜想假设
因为横截面的面积=宽×高,所以长方体体积=长×宽×高=长×(宽×高)=长×横截面面积。
二、原因分析,探究本质
1.肯定猜想,提出疑问
教师提问:“为什么横截面的面积×长就是长方体的体积?”
2.同桌讨论,反馈交流
预设:横截面的面积是3 平方分米,假设长方体的宽是3分米、高是1分米,那么就可以摆放3个棱长为1 分米的小正方体,体积为3 立方分米。长方体的长为5分米,则可以摆5列,所以一共可以摆放15 个棱长为1 分米的小正方体,体积就是15 立方分米(如图2)。算式:3×5=15(立方分米),即长方体体积=横截面面积×长。

图2
三、方法总结,得出结论
1.层层追问,促发深思
教师提问:“如果已知前面的面积和宽(如图3),能求出长方体的体积吗?”引导学生发现:长方体体积=前面的面积×宽。

图3
教师提问:“如果已知上面的面积(如图4),还需要什么条件才能求出长方体的体积?”引导学生发现:只要再知道高是多少就可以求出长方体的体积了,长方体体积=上面的面积×高。
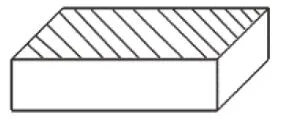
图4
2.分析归纳,总结方法
教师提问:“你们发现了什么?”
小组讨论后小结:长方体体积=某一个面的面积×与这个面垂直的棱的长度。统一表示为“长方体体积=底面积×高”。
四、拓展延伸,提炼模型
教师出示题目:下图的体积(如图5)可以用“底面积×高”来计算吗?

图5
让学生先用“底面积×高”求出体积,再将图形分割成两个长方体求出体积,最后比较两个结果以验证正确性。
教师提问:“你们有什么发现?”
学生发现此类图形同样可以采用“体积=底面积×高”的公式进行计算。
教师进一步提问:“经过刚才的研究,你知道哪些图形可以应用‘底面积×高’来求体积?”
学生展开讨论,并总结:由底面平移得到的图形、形状为上下均匀的柱体都可以用“体积=底面积×高”来计算。
上述教学过程改变了先认识底面积,再通过公式推导得出“长方体体积=底面积×高”这一结论的方法,而是从任意一个面的面积出发,引发学生的认知冲突,使学生深入理解公式的本质。

