超黏液体动力学模型对聚合物体系的适用性
任春晓,杨 晔,蒋斯麒,国 欣,王智远,张 帅,马成龙,张佳辉,胡玉峰*,刘植昌*
(1.中国石油大学(北京) 化学工程与环境学院/重质油加工国家重点实验室,北京 102249;2.中国石油石油化工研究院 新材料研究所,北京 102200; 3.中国石化工程建设有限公司,北京 100101)
玻璃化转变温度(Tg)附近的过冷液体被称作超黏液体。 玻璃态在日常生活中普遍存在,包括大多数工程塑料和光导纤维等,这使得功能性玻璃成为21 世纪最重要的高性能材料之一, 而其设计和制造过程高度依赖于超黏液体动力学的研究。 为了确定玻璃化转变理论的发展方向,需要明确描述超黏液体动力学 [黏度和松弛时间(τ)] 方程是发散型方程还是非发散型方程更适宜。 之前的报道已在发散型还是非发散型方程更适于拟合超黏液体动力学数据方面做了大量工作,但有关研究多限于小分子有机物[1-4],且较少考虑无限高温黏度(τ0)与无限高温松弛时间(η0)拟合值的合理性。 另一方面,在设计、制造和使用玻璃态聚合物材料时必须考虑物理老化所带来的物性变化,但如何定量考虑这些变化是超黏液体动力学模型研究中面临的一个挑战,因其关键在于定量描述对生产实践最重要、但也最难处理的 物 理 老 化 的 非 线 性 行 为[5]。 Narayanaswamy-Moynihan 方程和启发式非线性的Adam-Gibbs 方程是定量描述该非线性行为最常用的方程[5]。 这些方程的关键参数,比如Narayanaswamy-Moynihan方程里的常数x(其值不小于0 但不大于1)和活化焓Δh*(即过冷液体在温度稍高于Tg时的有效活化能)随材料而异,并且是通过Vogel-Fulcher-Tammann(VFT)方程的参数[Vogel 发散温度(T0)和脆性强度系数(D)]来确定的,而VFT 方程的参数T0和D 的值是通过拟合温度稍高于Tg时超黏液体的动力学数据获得。 VFT 方程是典型的发散型方程,因此,研究发散型方程还是非发散型方程更适于描述聚合物的超黏液体动力学,对确定Narayanaswamy-Moynihan 方程的关键参数x和Δh*, 进而定量描述物理老化的非线性行为非常重要。 从实际角度来看,Tg是最重要的特征温度, 因为利用该温度可将玻璃态与液态区分开,因此合理预测Tg值具有重要意义。本工作将利用聚合物超黏液体动力学的实验数据研究典型发散型和非发散型方程的适用性。由于Tg附近的区域是真正存在问题的区域, 因此将重点加以关注;由于τ 的实验数据比黏度数据更精确,所以利用其开展研究;同时,选择τ 实验数据相对准确的体系开展研究(例如文献[1]和[6]报道的体系),考察发散型和非发散型方程对Tg的预测性。
1 过冷液体动力学模型及拟合原理
1.1 发散型方程
此类方程的代表是VFT 方程[7]:
式中:τ0、D 和T0为拟合常数;T 为实际温度。由于T 趋近于T0时τ 趋近于无穷大,文献中认为T0定义了τ 的发散点,VFT 方程似乎描述了T0时发散的Super-Arrhenius 行为[7]。 该范式引导科学家们提出了发散型动力学理论, 包括亚当吉布斯理论[8]和随机一阶过渡理论[9]等。主流观点也据此认为,过冷液体的陡峭性慢化反映了由VFT 方程描述的、在T0时向τ 趋近于无穷大状态转变的相变[7,10]。
1.2 非发散型方程
非发散型方程包括Bassler-Avramov(BA)方程[1]
和Mauro-Yue-Ellison-Gupta-Allan (MYEGA)方程[11]
式中:τ0、A、n、K 和C 均为拟合常数;T 为实际温度。 上述方程表明不存在固定的温度,如T0,趋近此温度时τ 趋近于无穷大,因此被称为非发散型方程。
1.3 拟合原理
令τ0的拟合值在合理范围内(10-13~10-14s),利用MATLAB 进行最小二乘法拟合,通过最小化误差的平方和寻找数据的最佳函数匹配。 就本工作的模型拟合而言, 对于给定的一组实验数据(T,τ),假定其满足式(1)~式(3)的方程,为了求取各方程的参数τ0和D 及T0、τ0和A 及n、τ0和K 及C 的最优解,对于每个Ti(i 等于1,2,3...n),各方程的拟合值[τi(拟合值)]和相应实验值[τi(实验值)] 之间差值的平方和, 即残差平方和(SSE)应该最小:
式中:N 为实验数据点的数目。
2 结果与讨论
2.1 模型拟合结果
所研究聚合物三个方程的拟合结果与文献所查询Tg数据的对比见表1 和图1, 可以看出VFT 方程能准确拟合聚合物过冷液体的ln τ,而非发散性方程的拟合效果较差。
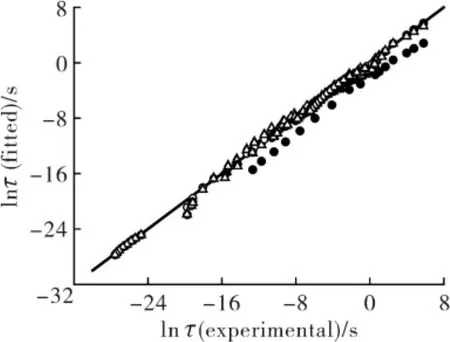
Fig 1 Comparison of fitted and experimental ln τ of polymer supercooled liquids by divergence and non-divergence equations
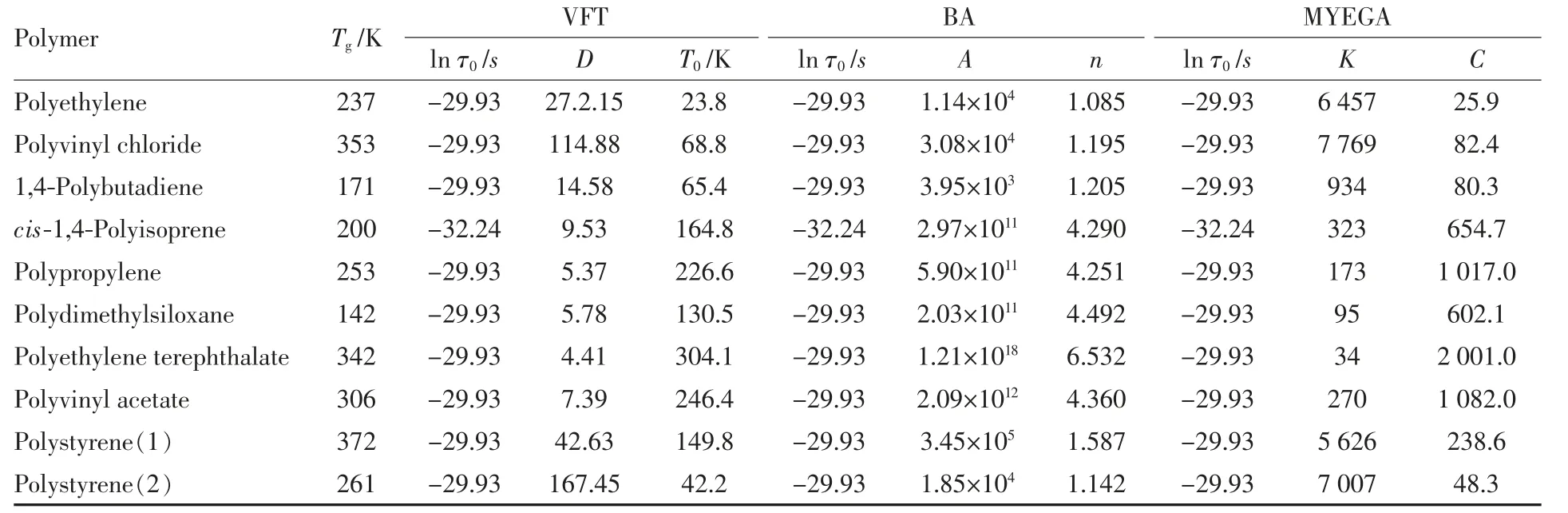
Table 1 Fitted parameters of three equations for ln τ values of polymers
2.2 拟合结果误差分析
三个方程拟合结果的均方根误差列于表2,可知VFT 方程的拟合均方根误差明显小于非发散型方程, 而BA 方程和MYEGA 方程对部分聚合物体系的拟合均方根误差较大,拟合结果不够理想。
图2 为三个方程拟合效果的残差分布图,可以看出VFT 模型的大部分残差值分布在0.4 附近,仅有少数例外。 当Tg/T 小于0.7 时三个方程的残差均接近0,而大于0.7 时残差逐渐增大,特别是大于0.8 时开始出现残差大于0.4 的情况。残差值位于0.4 之外的数据点多为非发散型方程的拟合结果,说明聚合物的过冷液体动力学更适于用VFT 方程描述。
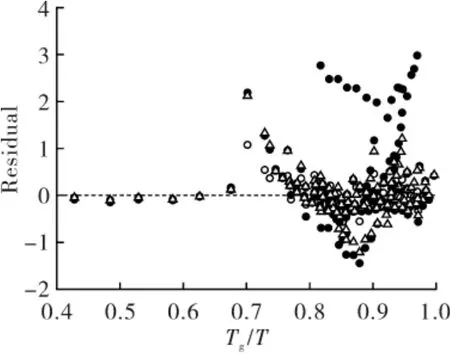
Fig 2 Distribution of residuals relative to Tg/T for fitted and experimental values of three models for polymer systems
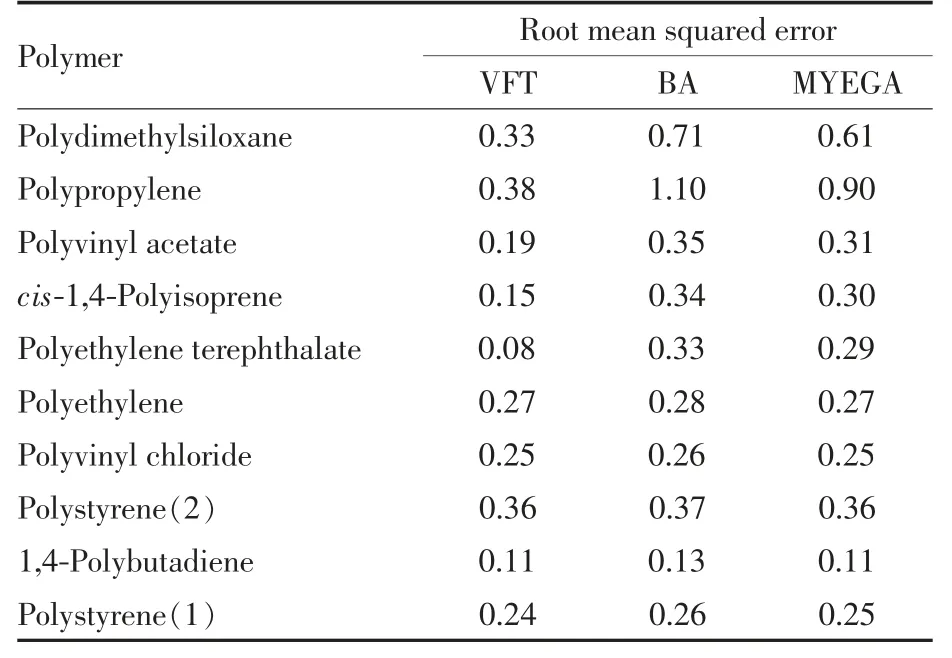
Table 2 Comparison of root mean square error of three equations for ln τ of polymers
2.3 Tg 预测结果分析
以τ 为100 s 时通过方程拟合得到的温度作为Tg的预测值 (Tgpred), 各聚合物Tg的实验数据(Tgexp)与三个方程的预测值以及二者的残差列于表3,可知三个方程的预测结果相近,且VFT 方程残差的平均值为10 K,小于非发散型方程。
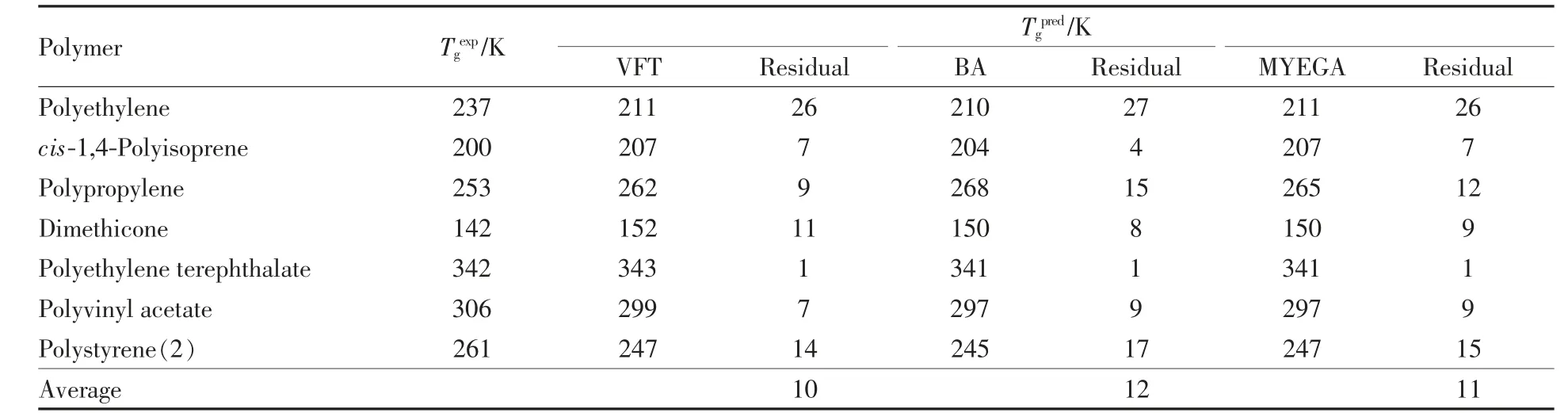
Table 3 Comparison of experimental and predicted Tg for typical polymers
3 结 论
聚合物的过冷液体动力学均最适宜使用VFT 方程描述, 其拟合精度优于非发散型方程,不仅总体的拟合偏差最小,具体到每个数据点也有最小的残差。VFT 方程对聚合物Tg的平均预测误差也是最小。

