基于离散元-有限元联合算法的纤维流场变形行为

董关震,姜 茜,钱晓明,吴利伟

(1.天津工业大学 纺织科学与工程学院,天津 300387;2.天津工业大学 先进纺织复合材料教育部重点实验室,天津 300387)

在纺织过程中,纤维的动态特性往往会影响织物结构性能,因此通过设计流场引导纤维运动是一种有效的质量控制手段。利用气流可实现对纤维的加捻、运输等过程。利用气流控制纤维具有纤维磨损率小、纤维分布均匀、纤维排列可调控以及生产效率提升等优势,其在诸多工艺环节如气流纺纱[1-2]、气流成网[3]、梳理成网[4-6]等均有应用。然而纤维在气流力作用下伴随着高度柔性变形与纤维间的碰撞,且流场分布差异对纤维运动过程与最终取向存在密切联系,因此对纤维在流场作用下的变形转移机制进行研究对于指导纺织生产至关重要。

利用计算流体动力学(CFD)获得流场计算结果,再通过构建的纤维动力学方程模拟纤维在流场中的运动已成为一种重要研究手段。利用CFD可以解除环境条件的限制,且其具备模型改进便捷、时间成本低等优势,以其针对纺织流场的研究正在不断发展。由于二维模型始终无法考虑纤维在真实三维空间中的运动与变形,相关流场研究逐渐从二维流场扩展至三维[7-9]。基于纺织流场的特性,相关流场模型的应用也在逐渐发展,Jin等[10]采用大涡模拟研究了转杯纺纱中转杯气流的涡特性,相比于k-e模型等传统RANS模型,LES模型捕捉到了更多非定常非平衡大尺度效应与拟序结构,且与直接数值模拟相比减少了计算成本。不同纤维模型在气流作用下会呈现不同形态,纤维模型主要分为2类,一类是刚性模型,如圆球[5,11]和圆柱模型[12],由于刚性模型无法改变其形状,因此只能近似表征纤维聚集形态,没有足够的自由度来模拟纤维的变形;另一类是柔性模型[13-15],可以实现弯曲、拉伸和扭转等情况。纤维与流体的耦合形式也会影响纤维的变形结果。在颗粒为稀相时使用流固单向耦合方法[16]计算纤维运动可以减少计算量,但随着颗粒浓度的增加,颗粒运动对流场的反作用逐渐增强,此时使用双向耦合[17-18]才能保证计算结果的准确性。目前大量纺织流场中的研究忽略了纤维柔性问题,使得对纤维动态转移与弯曲变形的行为认识不足。此外柔性纤维多针对单纤维,而忽略了纤维流中多纤维的交互,不利于预测纺织品结构与性能。

本文拟构建三维流场与柔性多球链纤维模型的流固耦合动力学模型,基于欧拉-拉格朗日算法Euler-Lagrange建立流场与柔性多球链纤维模型间的耦合作用关系,揭示单根柔性纤维在气流场中的瞬态受力变化与弯曲变形机制以及纤维簇在差异流场中的转移演化差异,以实现高变形多数量纤维的动力学计算模型构建。

1 仿真建模

采取数值模拟中欧拉-拉格朗日算法Euler-Lagrange方法求解,将空气视为连续相,颗粒视为离散相。耦合执行如下:①根据实际问题,可以依照时间步长、时间步数计算1个时间步内的流态,或直接进行稳态计算得到稳定流态;②通过耦合接口将流场作用在颗粒上的力传递给颗粒受力点;③通过引入的接触模型与黏结模型,计算柔性纤维各点在流场作用下的运动;④更新颗粒位置,若为双向耦合计算,则将纤维对流场的反作用反馈至流场,更新流场再次循环直至收敛,若为单向耦合计算,则纤维根据空间上更新的流场力进行迭代计算至收敛。⑤耦合计算结束,获得纤维受力过程与形貌变形演化。整体流程如图1所示。

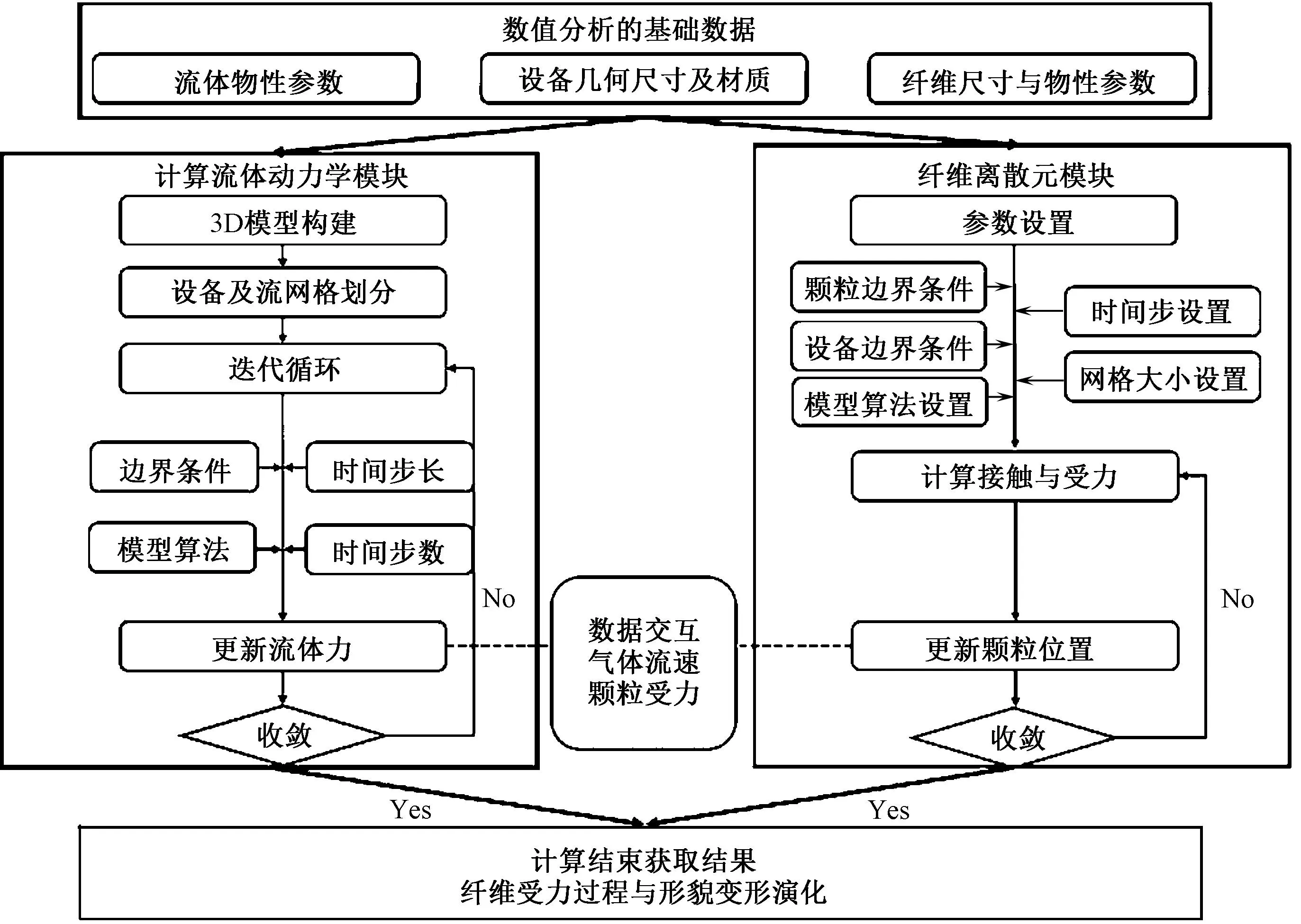
图1 CFD-DEM耦合过程

1.1 连续相模型

两相耦合模型中,气体设为连续相。假设气体不可压缩,控制方程为:

div(ρu)=0

(1)

(2)

式中:ρ为气体的密度,kg/m3;u为气流速度矢量;ui为u在坐标分量xi方向的分量(i=1,2,3),m/s;t为时间,s;μ为动力学黏度,N·s/m2;p为压力,Pa;Si为xi方向的广义源项。

采用稳态流场求解器,对流项采用二阶迎风格式离散,使用基于压力基的SIMPLE算法求解流场。

1.2 离散相模型

本文构建的纤维可被视为由n个球形颗粒与n-1根弹性杆组成的柔性多球链,柔性多球链纤维模型如图2所示。在纤维链中,第a个颗粒只与第a-1与第a+1个颗粒相邻,第1个和最后1个颗粒分别组成纤维头端与尾端。

图2 柔性多球链纤维模型

在初始阶段,颗粒之间通过黏结键连接形成与纤维类似的柔性结构,粒子所受的力(Fn,t)扭矩(Tn,t)设为0,并在每一时间步递增调整,如式(3)～(8)所示。

δFn=-vnSnAδt

(3)

δFt=-vtStAδt

(4)

δMn=-ωnStJδt

(5)

(6)

(7)

(8)

式中:RB是黏结的半径,m;Sn、St分别为法向刚度和剪切刚度,N/m3;δt为时间步长,s;vn、vt为粒子的法向和切向速度,m/s;wnwt是法向和切向角速度,rad/s;Fn、Ft是法向和切向接触力,N;Mn、Mt是法向和切向扭矩,N/m;A为黏结面积,m2;J为转动惯量,kg·m2。

当法向σmax和切向τmax剪应力超过某个预定值时,黏结就会断裂:

(9)

(10)

黏结形成后,颗粒在气流作用下进行平移与旋转,动力学控制方程如式(11)(12)所示。

(11)

(12)

球形颗粒与流体产生相互作用,颗粒间的碰撞使用软球模型,弹性杆起到传递内力与连接形成纤维的作用,整体可以实现纤维的拉伸、弯曲与扭转,较为完整地考虑了纤维的物理特性。

1.3 流场结构与纤维模型设置

本文在三维渐扩管道状的流体域内进行计算模拟,并基于短纤维特征参数(见表1)设置离散元柔性链。流体域结构与特征参数见图3。

表1 短纤维参数设计

图3 流体域结构与特征参数

2 结果与讨论

2.1 喂入纤维与气流夹角对纤维变形的影响

为了比较喂入纤维与气流夹角对纤维变形的影响,设置左端速度入口为2 m/s,得到了图4所示的流道中心沿Y-Z剖面的流速分布与初始纤维位置。纤维在T=0时刻喂入,且与气流方向的夹角分别为0°、10°、20°。

图4 流道中心沿Y-Z剖面的流速分布与初始纤维位置

经过搭建的耦合计算平台获得了图5所示的纤维在出口附近固定位置的最终取向变形。图5(a)中纤维初始取向与中心流速方向平行,最终时刻纤维仍呈现伸直状态,这意味着气流只在沿纤维主体方向存在速度差时,纤维没有形成弯钩的趋势。只有纤维初始取向与中心流速方向呈一定夹角时图5(b)(c),纤维弯钩才会形成,且随着夹角的增加,最终形成弯钩的形态越明显。在角度为10°与20°情况下,指定的纤维头端、中端尾端位置颗粒为典型位置点如图6所示,由于Y方向为主要受力方向,因此对其进行Y方向的受力分析以进一步说明纤维形成弯钩的过程。

图5 纤维与气流方向不同初始夹角时的最终弯曲情况

图6 纤维典型位置点

图7(a)(b)示出纤维在3个典型位置出现明显受力差大小与时间的差异。当初始角度为10°时,纤维头端、中端和尾端在0.015 s 开始出现了1.84×10-10N 的受力差异,而当初始角度为20°时则在0.001 s时出现了1.2×10-9N的受力差异,说明20°时纤维弯钩效果最好,这是因为较早出现受力差异使纤维开始变形的时间提前,且较大的受力差异使纤维变形过程更为迅速。

图7 纤维典型位置点的受力、速度与时间的关系

纤维端受力出现差异到产生变形差异也需要时间,力对变形速度和位移的影响效果仍需确认。如图7(c)(d)所示,在纤维初始角度为20°时,典型位置点出现高速度差的时间更早(0.009 s<0.016 s),数值更大(0.30 m/s>0.15 m/s)。在尾端粒子与中端粒子的组成的A部分,由于尾端粒子处的气体流速较慢,而中端流速较快,因此尾端与中端粒子在气流力与沿纤维方向的拉力合力作用下,尾端粒子与中端粒子部分运动受限形成一个整体,且受力与速度在各时刻几乎保持一致;而在头端粒子与中端粒子的B部分,由于中端粒子处的气流流速比头端粒子处更快,因此头端受气流力方向与受纤维拉力方向一致,此时对应头端速度曲线的降低阶段。纤维为了达到受力稳定状态,纤维头端在合力作用下逐渐翻转,该过程中端对头端的拉力方向逐渐相反,当纤维中端拉力开始主导纤维头端运动时,头端速度曲线达到峰值。翻转后纤维各位置受力与速度逐渐趋于一致,纤维头端的受力与速度曲线向中端靠近,最终趋于稳定。速度曲线并未出现受力曲线因纤维内应力导致的震荡,因此纤维因气流作用导致的内应力差异对纤维变形的影响可以略不计。

通过图8纤维典型位置随时间在Y、Z方向位移的变化对纤维变形过程进行了探讨。从Z方向上的位置变化可以看出,纤维头端在Z方向上先上升后减小,这对应纤维头端的先上扬后下落形成弯钩的过程。随着纤维初始喂入角度从10°增加至20°,上扬峰值从0.5 mm增加至1.0 mm,且上扬至峰值的时间减少,符合上述的受力与速度分析结果,纤维中端与尾端位移无明显变化趋于平稳。从Y方向的位置变化可以看出,随着时间推移,纤维头端位置曲线逐渐沿Y方向靠近尾端,且由于纤维初始喂入角度的增加,头端纤维靠近尾端的速度越快,20°时头端向尾端靠近的程度最高,形成了近似中心弯钩的效果。而在纤维中端与尾端,二者在Y轴方向上随时间的位移变化始终保持一致,呈现较好的整体性。

图8 纤维典型位置点的位移与时间的关系

2.2 喂入纤维位置对纤维变形的影响

纤维在流场中的变形程度取决于气流力在纤维上的累积。上述研究已知,相同位置下纤维的喂入角度越大,气流累积作用越强使其具有更好的弯曲变形效果。为深入探究更多影响气流力累积的因素,进一步比较了在高纤维喂入角度下不同喂入位置对气流的累计效果。在纤维初始喂入角度为20°时,将纤维分别放置于入口速度为2 m/s的差异流场计算域的左端入口位置 I与中心位置 Ⅱ 处(见图3),图9为不同纤维喂入位置下纤维在位置 Ⅲ 的最终取向变形结果。相比与从位置Ⅱ喂入的纤维,将纤维从位置I喂入流场中时在位置Ⅲ呈现出更强的弯钩效应,说明纤维喂入位置也会显著影响纤维变形。从图10(a)(b)纤维头端、中端与尾端典型位置点的受力与速度变化曲线可知,从位置I喂入的纤维由于初始气流场较大的流速差异,在T=0.001 s时刻纤维头端与中端的受力差到达峰值为1.2×10-9N,远大于位置Ⅱ 喂入后在T=0.006 s时产生的2.57×10-10N峰值受力差,并导致纤维头端与中端的流速峰值差异分别到达0.34 m/s与0.26 m/s(如图10(c)(d)所示),最终使纤维上扬量从0.49 mm增加至1.00 mm。尽管流速差异会影响形态,但在此流场中不同初始取向、不同喂入位置的纤维各典型位置点会趋近于稳定速度0.7 m/s。

图9 固定位置的纤维变形情况

图10 纤维典型位置点的受力、速度随时间变化规律

2.3 纤维交互作用对纤维变形的影响

为了研究单根纤维与纤维簇在流场运动过程中的差异,以10 m/s的入口速度条件对渐扩管流场特征进行计算。纤维簇模型包含同上的25根相同特征参数的单纤维。纤维之间的接触力通过Hertz-Mindlin接触模型计算,计算结果如图11所示。单根纤维与纤维簇随时间变化的运动位置基本吻合,但变形演化情况存在较大差异。T=0 s时,单根纤维与纤维簇被分别放入模型左端相同位置;T=0.002 s时,单根纤维整体发生屈曲变形,而纤维簇中只有上层纤维存在屈曲变形趋势,上层纤维阻碍了下层纤维的运动与气流力作用,导致下层纤维仍保持原有取向;T=0.004 s时,由于流场中心流速高,纤维中端逐渐引导下端伸直,使曲折部分逐渐转移至纤维头端,使头端有上扬趋势,在纤维簇中,下层纤维开始阻碍气流运动导致上层纤维受气流作用加剧,上层纤维变形大于单纤,纤维簇开始发生分层。T=0.006 s时刻,单根纤维头端上扬形成弯钩,纤维簇中9根上层纤维呈现大弯钩效果,变形优于单根纤维,16根下层纤维呈现小变形,上扬趋势不明显。

图11 单根纤维与纤维簇在流场作用下的运动演化过程

对周围纤维对单根纤维的变形影响进行量化探究得到图12在纤维相互作用下纤维典型位置点受力随时间变化规律。从12(a)可以看出,只喂入1根纤维时,其在0.000 4 s时头端与中端形成了5.01×10-9N的峰值受力差,而将这根纤维放在纤维簇中心再放入流场时,0.000 4 s时其头端与中端只形成了4.44×10-9N的峰值受力差,相邻纤维的交互作用使峰值受力差降低了11%。另外还比较了纤维簇层间受力的差异,从高变形量的上层区域与低变形量的下层区域分别选取2根典型纤维,从图12(b)中得知,高变形量纤维在0.000 4 s时分别形成了7.3×10-9N与6.79×10-9N的峰值受力差,而低变形量纤维在分别在0.000 4 s时和0.000 8 s时形成了2.2×10-9与2.64×10-9N的峰值受力差,层间变形的差异是由于纤维交互作用与气流分布差异的共同结果。

图12 纤维相互作用下纤维典型位置点受力随时间变化规律

3 结 论

通过构建柔性多球链纤维模型并结合CFD-DEM耦合模型进行三维仿真计算的研究方法,从纤维初始取向与气流方向夹角、纤维喂入位置和纤维间相互作用方面对柔性纤维与纤维簇在差异流场中的弯曲运动进行了研究,得出以下结论。

①当纤维与气流对齐对称地放置在通道中心线时,纤维沿水平路径直线前进,纤维的倾斜打破了对称性,导致纤维传输路径的偏差和波动,初始纤维的倾斜程度越高时,纤维越早发生屈曲。

②纤维的变形程度与气流力在纤维上的累积密切相关,增加纤维在流场中的运动距离有利于气流力的累积,纤维到达相同位置处的变形加剧,直至各纤维位置点趋于相同速度。

③纤维簇中纤维在流速差和层间相互作用下呈现分层现象,上层少数纤维会比单根纤维更快弯曲,下层多数纤维则更慢,纤维层间作用使峰值受力差降低了11%,纤维簇阻碍了单根纤维变形,不利于纤维的均匀混杂。