三峡库区弯曲河段大偏角船桥碰撞力分析

郑霄阳, 范存斌, 王英森, 唐亮*, 余葵

(1.重庆交通大学山区桥梁及隧道工程国家重点实验室, 重庆 400074; 2.中铁二十二局集团第五工程有限公司, 重庆 400711; 3.重庆交通大学河海学院, 重庆 400074)

船桥碰撞作为一项复杂的冲击动力学问题,在桥梁防撞设计中,船舶最大撞击力的合理确定至关重要。

由于长江上游流域跨江大桥数量众多,受三峡水库蓄水的影响显著,重庆航段多座跨江大桥位于三峡库区,使得库区桥梁桥墩较高,抗水平撞击的能力较弱。水库的建成还使得通航水位不断提高,这也导致原来所建桥梁的更多桥墩处于水中,增加了船舶撞击的风险。

耿波等[1]采用《美国公路桥梁设计规范》(AmericanAssociationofStateHighwayandTransportationOfficials, AASHTO)的方法和三概率参数积分路径方法对粉房湾长江大桥进行船撞风险分析,计算桥梁的碰撞概率和年倒塌频率,对桥梁抗撞性能进行安全评估。王建国等[2]以安徽省望东长江公路大桥为背景,研究船桥碰撞时桥梁撞击位置的受损状况及结构响应,发现船艏与桥塔的损伤随撞击角度变化。付明春[3]通过动态模拟船桥碰撞过程,研究撞击深度和碰撞力对船舶结构的损伤情况。

目前,船桥碰撞的研究方法主要为有限元数值模拟计算法、动力简化计算法和静力计算法。在各国的相关规范中,对于船舶撞击力设计值均采用静力计算法,如美国AASHTO设计规范(2009)[4]、中国《公路桥涵设计通用规范》(JTG D60—2015)等[5-7]。由于中国在此领域规范数量较多,不同的撞击力计算公式中考虑的影响因素各异,选用的计算方式差异极大,计算所得最大撞击力大相径庭。合理选择相关规范计算桥梁抗撞设计值成了一个难题。

通过比较国内外关于船桥碰撞相关规范最大撞击力的计算参数,分析不同撞击角度下的船桥碰撞所产生的最大撞击力差异性。重庆外环江津长江大桥位于三峡库区典型桥区河道,地势高差较大,该区段水流湍急,河道弯曲、通航密度大,在此航段上发生船桥碰撞的风险较大。以此桥船桥碰撞安全风险评估为依托工程,通过运用有限元软件ABAQUS,建立了7 000 t级散货船和等比例斜拉桥模型。采用高流速下船舶侧撞角理论公式对船舶撞击角度进行计算,同时在船撞速度计算中采用考虑河道里程综合影响的计算方法,最终以撞击角度、撞击速度和水位高度作为变量,确定了12种不同情况下的撞击模型。通过12种工况进行数值模拟后,对撞击力时程曲线进行全过程分析,将模拟结果与规范计算数据对比,为三峡库区弯曲河段中的船撞力计算提供参考。

1 高流速、大偏角下理论公式及参数取值

1.1 最大撞击力计算的船桥碰撞规范

随着船桥事故的频繁发生,各国出于安全考虑,在通航桥梁设计中都需考虑进行抗撞设计。众多学者根据船桥碰撞理论及试验研究成果给出了船桥碰撞的简化计算公式,相关研究成果被采纳并运用到对应规范中,在计算船桥碰撞力上给出了不同参考公式,如表1所示。

表1 国内外关于船舶撞击力设计规范Table 1 Code for design of ship impact force at home and abroad

1.2 三峡库区河道各规范理论参数取值

各规范在理论分析船撞力,因素,参数,选取方法如下。

(1)《通规》常用于计算船桥正撞情况下的最大撞击力,撞击点通常是位于承台或桥塔横向宽度的中点处。船桥碰撞动态响应主要集中在0～1 s,因此撞击力计算公式中撞击时间参数T取1 s;漂浮物重力M选取7 000 t级船舶,船货总重为9 270 t,即9 270 000 kN。

(2)《铁桥规》在桥梁防撞设计中,常用于船只行驶方向与桥墩台面法线方向不一致的情况,但在计算说明中并未明确撞击点的位置。撞击力计算公式引入正弦sinα对不同撞击角度的船桥碰撞进行调整,在重庆外环江津长江大桥数值模拟的船桥正撞中,采用船舶行驶方向与撞击点法线方向的夹角,即α=90°;在侧撞和漂撞中,撞击角度为船舶行驶方向与横桥向的夹角,均为α=23°。

(3)《公桥规》适用于船舶满载货物和船舶撞击角度小于45°,在此情况下常用该规范计算船舶最大撞击力。在该规范计算中,考虑的计算参数较为全面,相关计算参数的推荐取值:浮连水质量系数CM,船艏正撞时宜取0.1～0.3,侧撞时宜取0.5～4.5。在实际工程中,通过船舶吃水与航道水深的比值来确定浮连水质量系数CM,由于重庆三峡航道水深为10～40 m,以7 000 t级散货船“广运77号”为典型船舶,该船船舶尺寸为116 m(总长)×16.6 m(型宽)×6.1 m(型深),满载吃水深度仅为4.07 m,船舶吃水与航道水深比值小于0.8,因此在正撞中浮连水质量系数CM取0.3,侧撞和漂撞中CM取0.5。几何尺寸修正系数η是由船体厚度ΔH与船艏高度Hs比值确定,此处修正系数η取值为1。在该规范5.1.5节中,船舶撞击速度有着明确的规定,撞击速度沿着航道中心线向两侧递减,采用该规范公式5.1.5速度曲线计算,此处省略计算过程,计算结果见表1。

(4)《AASHTO》是根据美国船桥碰撞事故资料来统计构建出试验模型[8],船舶正向撞击刚性墙试验后提出。其经验公式对于多种船舶类型均适用,如油轮、货轮、散货船等,适用于船头正撞桥墩的情况。公式在实际计算中采用的是等效平均碰撞力,考虑了船舶撞击初速度和船舶吨位对撞击力的影响,是目前全世界船桥碰撞领域应用最为广泛的规范。

(5)《欧规》出自欧洲统一规范Eurocode 12.7分册,选用了全欧最广泛统计意义下的代表船舶,其公式特点是兼顾了内陆航道和海洋的船舶碰撞计算。对于内陆航道的船舶,K=5 kN/m;对于海洋船舶,K=15 kN/m。

2 多角度船桥碰撞方式及相关参数计算

2.1 考虑撞击角度的三种典型撞击方式

船桥碰撞事故的发生因素较为多样,通常受“人为、船舶、通航环境”等因素的影响,导致了船桥碰撞方式存在不确定性。综合考虑各因素的影响,选取了三种典型的撞击方式进行分析(图1)。①船艏正撞桥塔,正撞是当前研究中最为典型的撞击方式;②船艏侧面撞击桥塔中部,导致因素常为驾驶人员判断失误或航道指示灯出现故障;③横漂船侧撞击桥塔,该撞击方式在目前的船桥碰撞研究中涉及较少,主要是恶劣天气情况以及不良航道环境导致船舶失控。如2017年8月23日,台风“天鸽”在广东珠海登陆,在强风及风暴潮增水的影响下,“顺宏海1188”轮、“泰华航8668”等船舶发生走锚失控漂移,其中四艘船舶相互压碰勾连在一起漂移至上游约2 km处的广东西部沿海高速公路磨刀门特大桥,与大桥非通航孔桥墩发生触碰,致使部分墩柱及梁板受损,并导致“顺宏海1188”轮倾覆沉没。

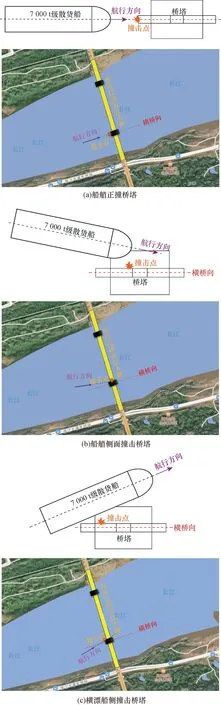
图1 船桥碰撞方式及实景展示Fig.1 Bridge collision mode and scene display

2.2 高流速下船舶侧撞角理论计算

船舶在航道上的航向,一般是按航道中心呈蛇形航迹左右摆动前进。船舶在行驶过程中受水流流态、流向、流速、风向、风速影响较大,加之重庆航段水流湍急、河道弯曲,因此船舶航行过程中会产生风流压偏角。根据研究表明[8-9],对船舶受横流影响的压偏角计算公式为

(1)

重庆外环江津长江大桥位于U形河道,横桥向与水流方向存在夹角,可能产生船舶航行的风流压偏角;同时,桥梁桥墩建设时,桥墩中心线与水流流向会产生夹角。这两个瞬时综合的结果,组成了偏航船舶与桥墩瞬时撞击的撞击角。两者角度的绝对值相加,即可得到最大侧撞角,表达式为

θ侧撞角=|α风流压偏角|+|β桥轴法线偏角|

(2)

根据重庆外环江津长江大桥桥区航道实测结果,7 000 t级船舶的航速为5.56 m/s,由于所处航道与水流流向不一致,水流会对船舶产生横流作用,因此需要通过风流压偏角和桥轴法线偏角来计算船舶侧撞角,该角度是船舶最大概率发生的侧撞角度。

2.3 考虑河道里程综合影响的船撞速度计算方法

撞击速度的影响因素有很多,如水流速度、船舶行驶速度等。撞击速度通常采用“失舵不失速”的计算方法[10],此方法确定的撞击速度将维持偏航前的线速度,改变的只是行驶角度和方向。如美国肯尼色河桥、中国广东九江大桥等桥梁,被撞塌的桥墩都远离航道中心线,且发生撞击时船舶速度并未下降。其中广东九江大桥被撞的桥墩距离航道中线为130.0 m,桥塌下后螺旋桨继续转动,并没有人去关机或者减速。上海海洋钢结构研究所对“失舵不失速”方法进行了修正,提出了考虑船舶速度沿桥轴线方向的分布及船舶意外等失速因素综合影响下的撞击速度计算方法。该方法考虑了河道流速在横向的分布是抛物线状,即主航道区域流速较大,航道边缘及外侧的流速较小。船撞桥墩计算选取速度时,应根据船舶所航行水域的水流速度依次调整,得到船舶行驶至各桥墩时不同的航行速度。具体计算公式为

Vx=V0-v0+vx

(3)

式(3)中:Vx为桥墩处典型航速;V0为船舶在航道内的正常行驶速度;v0为航道内中心流速;vx为距离航道中心x处的流速。

3 重庆外环江津长江大桥船桥碰撞数值模拟

3.1 工程概况

长江是中国内陆水上运输的重要要道,重庆外环江津长江大桥桥区航段位于三峡库区回水变动区,水位高差变幅大,河道情况复杂,水流速度差异显著,船桥碰撞事故时常发生。

重庆外环江津长江大桥位于重庆绕城高速南段,是重庆绕城高速公路的重要组成部分,是重庆绕城高速公路中规模最大的特大桥。该桥位于重庆市九龙坡区西彭镇李家河村,长江上游航道里程约721.1 km处,黄磏一期工程下游408 m,航道情况如图2所示。全桥长度为1.19 km,桥面宽36.5 m,跨江主桥跨径布置为(33.5+186+436+186+35.5) m,主跨长为436 m,主桥共长879 m,为结合梁斜拉桥。全桥设置两个菱型桥塔,滴水岩方向9#桥塔高度为167.29 m,南彭方向10#桥塔高度为172.19 m,在主梁下底板处设置一道横系梁。斜拉索均按照扇形布置,12 m为一个标准节段索距,桥梁总体布置情况及10#桥塔立面如图3所示。

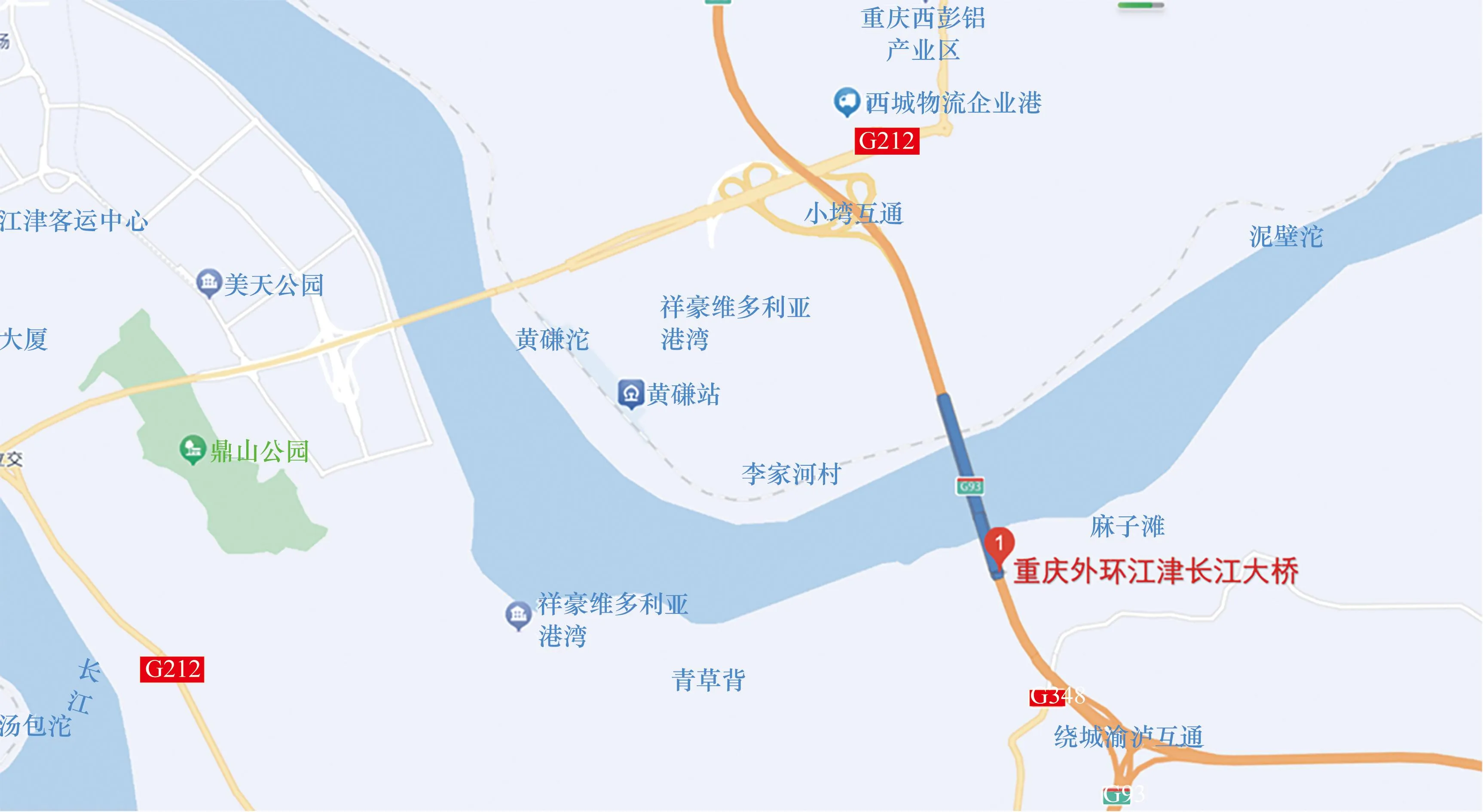
图2 重庆外环江津长江大桥及桥区航道图Fig.2 Chongqing outer ring Jiangjin Yangtze River bridge and channel map of bridge area

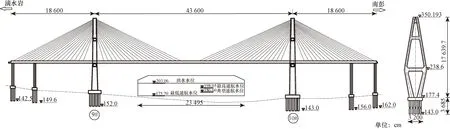
图3 重庆外环江津长江大桥总体布置图Fig.3 General layout of Jiangjin Yangtze River Bridge around Chongqing

重庆外环江津长江大桥按高速公路标准设计,设计时速为100 km/h,为双向6车道,最高通航水位为198.05 m,最低通航水位为175.70 m。索塔和承台分别采用C50混凝土和C40混凝土,在主桥左右两侧各设置2个辅助墩,墩身采用C40混凝土,桥墩桩基采用C30混凝土,全部桩基均为端承桩,共57根。

根据2017—2020年统计,此航段通航船舶吨级为3 000～7 000 t,占比95%。本桥船撞重要性等级为一级,通航代表船型的选取以《内河过闸运输船舶标准船型主尺度系列》(GB 38030—2019)标准船型为基础,结合《内河通航标准》(GB 50139—2014),采用5%准则确定设防代表船型[11],综合考虑后选取7 000 t级散货船作为代表船型。

3.2 船桥碰撞系统的力学模型

根据2020年重庆海事局的新闻报道,目前重庆航段7 000 t级散货船的代表船型为“广运77号”,主尺度为116.0 m×16.6 m×6.7 m,空载情况下,船身质量为2 270 t,故满载情况下,船货总重量为9 270 t。

3.2.1 7 000 t级船舶有限元模型

船舶为桥区航段典型的7 000 t级球鼻艏散货船,船桥碰撞过程中主要关心船桥相互作用力和碰撞位置变形情况,因此在船舶有限元建模中根据其不同部件的重要程度而区别详细程度[12]。船舶根据实船图纸进行建模,将结构分为前端球鼻艏、中部船身和后部船舱。为提高计算精度,在网格划分中对前端球鼻艏结构网格进行加密。船尾在本次模拟的碰撞过程中不发生任何接触和形变,为了简化船体,将船尾结构进行简化处理,建立为等长度船身结构形式,以保证所建船舶模型长度和质量与真实船体一致。7 000 t级船舶吨位(含载重)合计为9 270 t,船舶尺寸为116 m(总长)×16.6 m(型宽)×6.7 m(型深),船舶满载吃水深度为4.07 m,全船共划分单元99 978个。船舶的有限元计算模型,如图4所示。

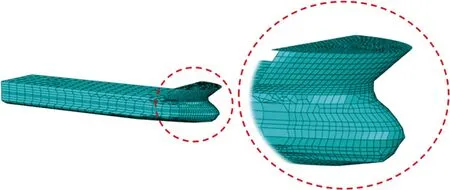
图4 7 000 t级船舶有限元模型Fig.4 Finite element model of 7 000 ton ship

3.2.2 桥塔精细有限元模型

南彭侧桥塔高度为172.79 m,在低水位时船桥碰撞撞击点位于承台,故数值模拟桥塔有限元模型以南彭侧10#桥塔为例。桩基础采用端承桩进行边界条件设置;桥塔被撞区域加密网格,采用C3D8R减缩积分单元进行划分,其中精细划分单元数量为37 865,模型单元总量为59 516,如图5所示。

图5 桥塔有限元模型Fig.5 Finite element model of pylon

3.2.3 数值模拟相关参数设置

考虑钢材与混凝土之间触形式为表面接触,摩擦系数为0.25。通过附加质量的方法替代水体对船舶的作用力,此处采用附加10%的船体重量[13],船货质量与10%的附加水质量总和为10 197 t,通过修改船体密度实现。在材料上,全船采用弹塑性本构模型,运用了各向同性和弹塑性随动强化材料。

3.2.4 桩土相互作用

根据重庆外环江津长江大桥的地质勘查资料,该大桥处的土体为砂性土。通过采用非线性弹簧(长度1 m)来模拟等效土体对桥塔的侧压力,取内摩擦角为35°。由于此处地质条件优越,桩基采用端承桩,经过试算,在发生船桥碰撞时,桥桩的最大水平变位小于40 mm,因此在发生碰撞时弹簧的角度变化可以忽略不计。

根据端承桩的力学特征,限制弹簧外围末端节点位移,对桩的底部单元节点的竖向位移进行约束。

3.3 船桥碰撞计参数的取值

3.3.1 四种水位高度下的撞击角度计算值

根据2.2节式(1)和式(2),在综合考虑航速、横向流速、风流压偏角和桥法线偏角后,船舶侧撞角计算结果如表2所示。

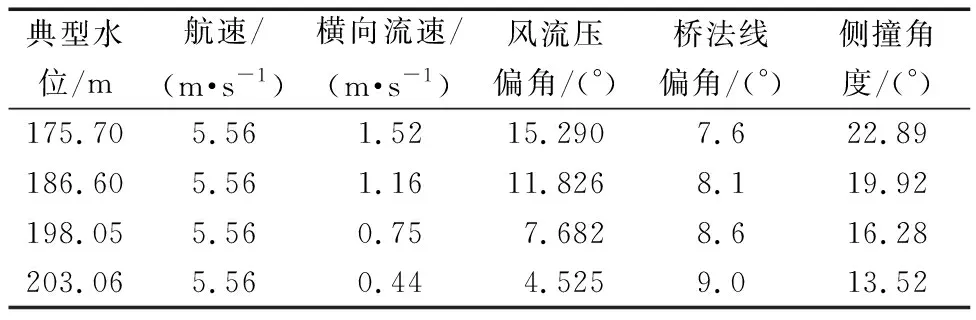
表2 10#墩处船撞速度表Table 2 Speedometer of ship collision at pier 10#

根据表2计算结果,桥区在上述四种水位情况下,7 000 t级船舶通过主墩时偏航撞击角度最大为22.89°,最小的撞击角度为13.52°。综合考虑各方面的安全因素之后,将设防船型的偏航撞击角度取为23°。

3.3.2 四种水位高度下的撞击速度计算值

撞击高度取决于水位高度和船舶干舷高度,该桥的最高通航水位为198.05 m,最低通航水位为175.70 m,典型水位为186.60 m,洪水位为203.06 m,如图6所示。对于7 000 t级船舶,考虑船舶干舷高度为2 m。在最低通航水位时,船舶撞击点在桥塔的承台处,在最高水位和洪水水位时,船舶撞击点在桥塔。根据2.3节式(3)计算出不同水位高度下的船舶撞击速度如表3所示。

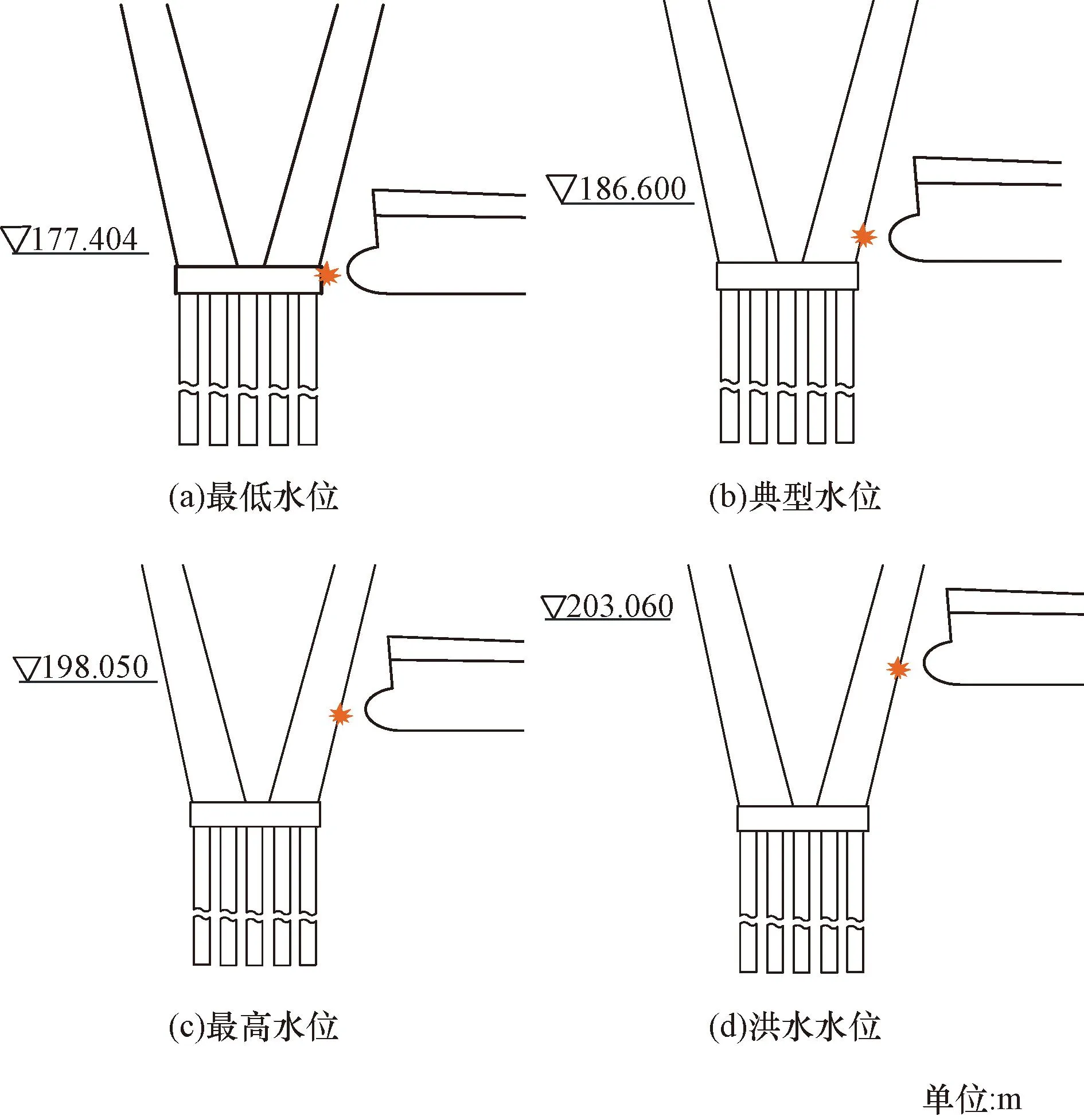
图6 各通航水位船舶撞击示意图Fig.6 Schematic diagram of ship collision at each navigable water level

表3 主墩处船撞速度表Table 3 Ship collision velocity at main pier

3.4 数值模拟结果

撞击角度分别为0°和23°,4种水位下计算了7 000 t级散货船在船艏正撞、船艏侧撞以及横漂侧撞,共计12种工况,如表4所示。

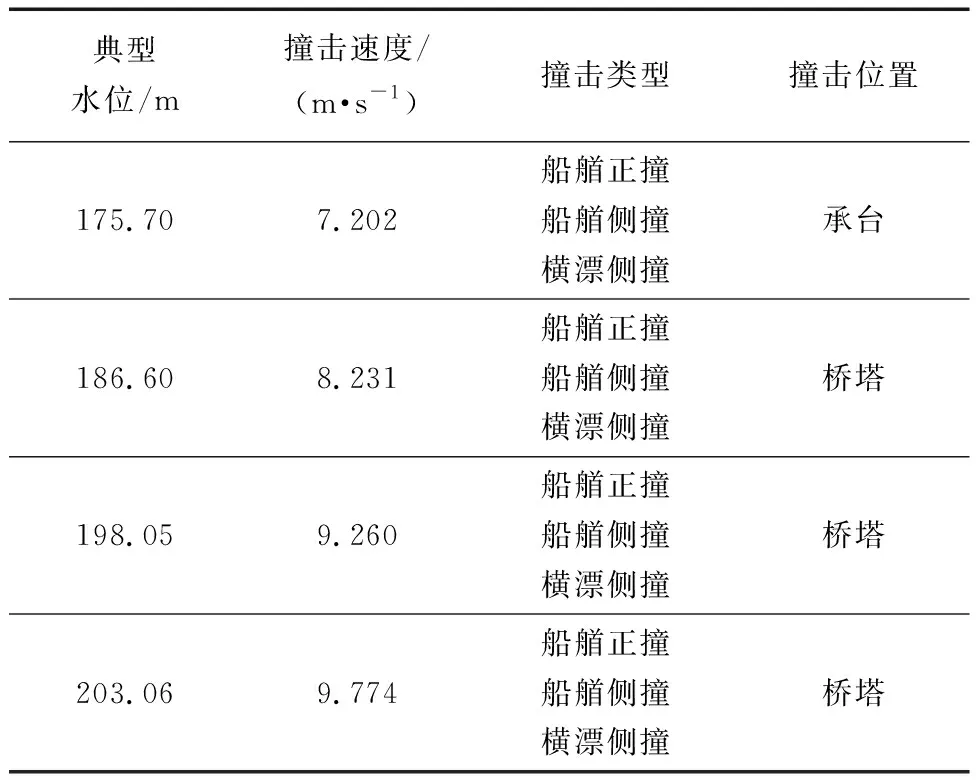
表4 计算工况Table 4 Calculation conditions

图7所示为船舶撞击过程中的时间—撞击力曲线图,时程曲线图包含了低水位、典型水位、高水位以及洪水位4种工况。

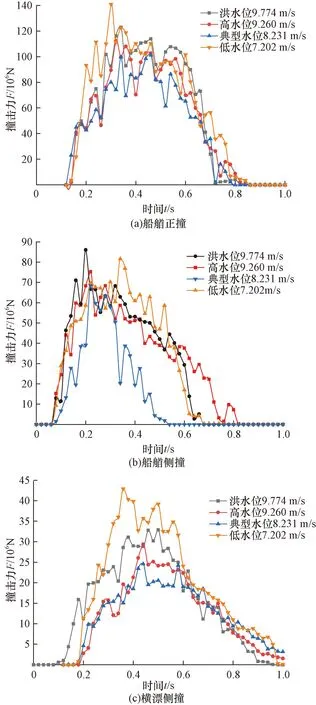
图7 10#墩撞击力时程曲线图Fig.7 Time history curve of impact force on block 10#

3.5 曲线拟合

根据3.4节中的数值模拟结果,在不同水位和撞击速度下的撞击力时程曲线呈现出半正弦波形态,与现有的研究成果较为吻合。孟德巍等[14]建立了半波正弦简化公式拟合了碰撞力时程曲线的形态,此研究认为碰撞力的峰值将出现在碰撞持续时长的中点,兰成坤等[15]通过引入正弦函数对上述方法进行了函数修正,得到了较为准确的拟合公式,即

f(t)=π(mt2+nt)

(4)

式(4)中:F为碰撞力,N;A为动力荷载峰值,N;t为碰撞响应过程中的时间点,s;t为碰撞持续时间,s;TC为响应峰值对应的时间点,s;a、b、m、n为拟合分项系数。

根据船桥碰撞数值模拟结果显示,在发生碰撞响应后,撞击力逐渐攀升至峰值后下降,该碰撞力峰值与相邻的碰撞力会产生较大的落差,同时在整个响应过程中,撞击力时程曲线会产生较大波动,因此将撞击力峰值作为安全衡量标准与实际相差较大。

本文中主要考虑船舶速度和碰撞角度两个因素,拟合各个参数和船舶速度和碰撞角度之间的关系式,通过拟合曲线的动力荷载峰值进行安全评估。限于篇幅,以位于低水位时船艏正撞10#墩为例,对有限元时程曲线进行拟合如图8所示。

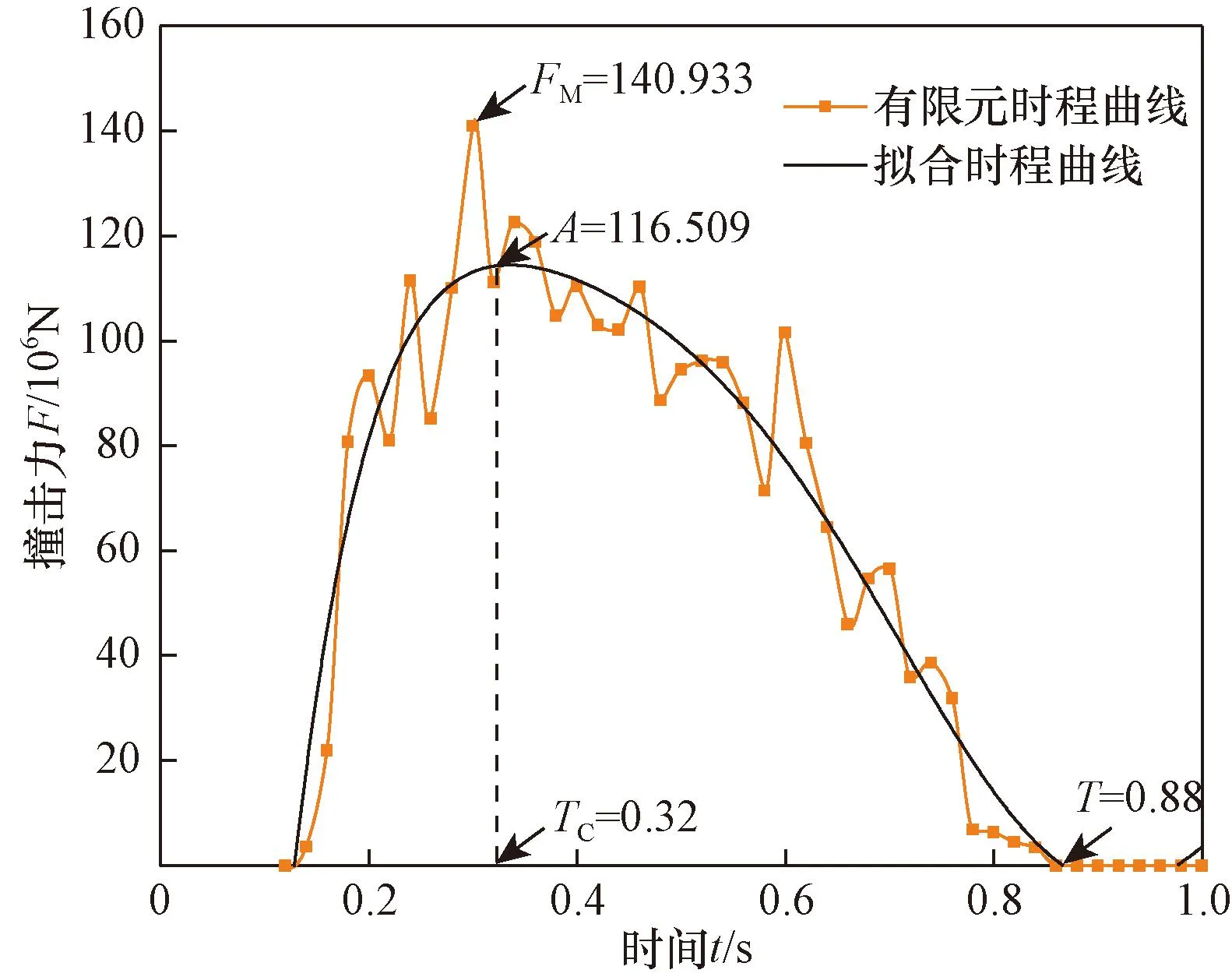
图8 撞击力时程曲线拟合示意图Fig.8 Schematic diagram of impact force time history curve fitting

3.6 各规范理论公式计算值与分析

为分析撞击方式及角度对船舶最大撞击力的影响,根据1.1节表1中各规范的计算方式和取值,计算相同水位高度、船舶质量、撞击速度及撞击角度下各规范的撞击力设计值,通过3.5节中时程曲线的拟合方式对3.4节的数值模拟结果进行拟合,绘制了数值模拟结果与国内外相关规范计算值对比图。如图9所示,位于低水位航行的船舶在发生船桥碰撞时,仿真模拟值将远大于各规范计算结果,造成这一现象的原因应是撞击点位于承台,在发生碰撞时船舶球鼻艏将直接与承台接触,截面刚度大所致。

图9 船桥撞击模拟值与各规范计算值对比Fig.9 The simulated value of 23° yaw drift collision is compared with the calculated value of each code

由图9(a)可知,除低水位船桥碰撞模拟值外,在其余水位下的模拟结果显示,最大撞击力位于AASHTO与《通规》之间,更加贴近AASHTO的数值计算结果,说明了AASHTO在船艏正向撞击且撞击点为桥塔时的碰撞计算具有较强的适用性,对于三峡库区高变幅水位下的斜拉桥碰撞计算具有很强的参考价值,还表现出两者规范在计算公式上存在差异,但两者在计算船舶正向撞击桥塔时结果较为相近。

对于考虑撞击角度的船桥碰撞而言,《铁桥规》与《公桥规》在最大撞击力的计算中明确将撞击角度作为其中一项计算参数,但两者计算值具有较大差距。相较于中国其他规范,《公桥规》在船舶撞击速度取值上做出了明确规定,船舶撞击速度沿航道中心线向两侧逐渐递减,本文中考虑的船舶撞击点位于航道中心线至3倍船长区间内,船舶撞击速度按照《公桥规》中公式5.1.5速度曲线计算。通过图9(b)的对比结果可以看到,除低水位外的数值模拟结果位于《公桥规》和《欧规》之间,《公桥规》考虑了撞击速度和撞击角度两大重要参数且与模拟结果吻合程度更高,更加贴合船艏侧撞的实际情形。

根据图9(c)可知,当撞击点位于桥塔时,船舶在偏23°漂撞情况下所产生的最大撞击力大致为22×106～29×106N,与《铁桥规》数据吻合程度较高,相较其他两种方式的撞击而言,该情况的最大撞击力仅为正向撞击的1/4左右,但船舶漂撞在历年的船桥碰撞事故中发生概率高,主要是由于船舶失控撞击下游桥梁,因此船舶的撞击方式和角度具有不确定性。在所有的船桥碰撞中,船舶正撞产生的最大撞击力大于侧撞和漂撞,但最大撞击力只能作为衡量船桥碰撞风险的指标之一,存在撞击角度的侧撞和漂撞不仅应考虑横桥向的抗撞能力,顺桥向的抗撞性也要考量。

3.7 多角度变化的船艏漂撞分析研究

为了进一步研究撞击角度对船桥碰撞带来的影响,选取了撞击角度为0°、10°、20°、…、80°的典型水位船艏侧撞为例,数值模拟所得的最大撞击力与《公桥规》计算值进行对比分析,如图10所示。

图10 数值模拟值与规范计算值对比Fig.10 Comparison between numerical simulation value and standard calculation value

在撞击角度不断改变的船舶侧向撞击桥塔的计算对比中,《公桥规》计算值与模拟值在撞击角度约为15°时相等,大约以撞击角度15°作为分界线,随着角度的增加或者减小,规范计算值与数值模拟结果差距逐渐增大。当撞击角度位于10°～45°时,《公桥规》计算值与模拟值差值在±10×106N内,尤其是撞击角度位于10°～25°时,该规范与模拟结果更为接近,体现出《公桥规》在该角度范围下的船艏侧撞计算中具有很好的参考价值,同时也印证了在《公桥规》中的撞击角度修正系数仅仅只能使用在0°～45°的船桥碰撞计算中。

在中国相关规范中考虑撞击角度的最大撞击力计算式较少,《铁桥规》通过运用正弦及动能折减系数,在一定程度上能对存在角度的船舶漂撞产生的最大撞击力进行估算。区别于其他规范,《公桥规》利用独特的分段函数对船舶撞击速度进行计算以及采用了含有余弦的撞击角度修正系数。

4 结论

在内河航道的船桥碰撞是一项复杂的工程问题,通过以重庆外环江津长江大桥作为工程依托,研究了位于三峡库区高变幅水位下的3种碰撞形式,根据在4种通航水位下共12种工况的数值模拟结果与国内外规范进行对比分析,得到如下结论。

(1)国内外关于船桥碰撞的规范计算结果差异较大,各理论公式选取了不同的计算参数,考虑的撞击点均位于桥塔。在船桥正向碰撞计算中,AASHTO与数值模拟结果吻合程度高,适合用于计算船舶正向撞击桥塔情形;在侧撞中,《公桥规》更适用于小角度和高流速下的船桥碰撞计算;相较于正撞和侧撞,漂撞所产生的撞击力较小,《铁桥规》在此情况下与模拟结果更加接近。

(2)撞击角度的改变对船桥碰撞具有很大的影响,船舶与桥梁发生侧向碰撞中,《公桥规》在撞击角度位于10°～45°时计算所得的最大撞击力具有较强的参考性,尤其是撞击角度在10°～25°的船桥碰撞中计算结果更加准确。

(3)在三峡库区高变幅水位下,航运环境较差,船舶漂撞在历年的船桥碰撞事故中发生概率高,船舶的撞击方式和角度具有不确定性。在所有的船桥碰撞中,侧撞最大船撞力大约为正向撞击的2/3,而漂撞的最大船撞力约为正向撞击的1/4,但最大撞击力只能作为衡量船桥碰撞风险的指标之一,侧撞和漂撞不仅应考虑横桥向的抗撞能力,顺桥向的抗撞性也要考量。