基于RF-WOA-VMD-BiGRU-Attention的神经网络模型在海浪预测中的应用

李练兵, 张燕亮, 吴伟强, 魏玉憧, 李佳根, 卢盛欣

(1.河北工业大学人工智能与数据科学学院, 天津 300130; 2.河北建投海上风电有限公司, 唐山 063000)

目前海浪预测[1]的方法主要分为3种:基于物理的数值方法,基于经验的统计方法和机器学习方法。基于物理的数值方法是理论驱动的,利用求解海浪的控制方程进行预测,但是只对海域比较宽阔,环境比较平缓的海浪有较好的预测结果。迄今为止,最成熟的基于物理的波模型是第三代海浪波模型[2],但是依旧需要大量的计算时间,这也是日常使用中最大的限制。基于经验的统计方法在预测中使用的假设模型,根据从实际得到的与过程有关的数据进行数理统计分析,预测的效果一般。如自回归模型和自回归移动平均法。机器学习方法通过输入和输出的大量历史数据描述了更全面的输入输出关系,例如,利用人工神经网络(artificial neural network, ANN)[3]预测海浪数据,ANN对于建立复杂非线性映射拟合函数的能力非常显著。然而,上述神经网络自身存在的缺点是忽略了数据对时间的依赖性,使得预测模型对噪声十分敏感,预测准确性下降[4]。(long short-term memory, LSTM)和(gated recurrent unit, GRU)都是循环神经网络(recurrent neural network, RNN)的进阶版本,LSTM[5]是对RNN的细胞结构进行优化,GRU则是将LSTM从内部结构上进行进一步的优化。双向门控循环单元(bidirectional gated recurrent unit,BiGRU)在GRU上增加了一个反向隐藏层,这样正向隐藏层和反向隐藏层可以互相利用隐藏层中的数据,预测结果会更加准确。该模型的预期效果在数据集较大的情况下具有更快的训练速度、更高的准确性、更好的处理顺序信息、更少的内存消耗,提高海浪预测模型预测精度[6]。研究结果证明GRU的预测性能明显高于LSTM和RNN,并解决了RNN存在的梯度爆炸性消失和长期记忆力不足等问题。

为了解决上述的各类问题,现提出一种结合随机森林、鲸鱼算法、变分模态分解的双向门控循环单元的海上风电场海浪预测模型,选取河北乐亭菩提岛风电场近一年来的海上数据作为预测模型的基础数据。首先使用随机森林筛选出与海浪波高相关性较强的环境特征数据,应用WOA(whale optimization algorithm)-VMD(variational mode decomposition)模型进一步降低数据噪声,提高模型的输入质量。最后将BiGRU与随机森林的注意力机制相结合,结合后注意力机制将为BiGRU的隐藏层分配不同权重并加强关键信息的影响,搭建出RF-WOA-VMD-BiGRU-Attention海浪预测模型。

1 RF-WOA-VMD-BiGRU-Attention神经网络模型构建

1.1 数据准备

1.1.1 海况数据采集

采取乐亭菩提岛风电场以观测站的海况数据作为样本数据集,样本数据集中采集了2020年1月1日0时—2021年12月31日24时的相关海况数据。表1为一段时间内的原始海况数据。

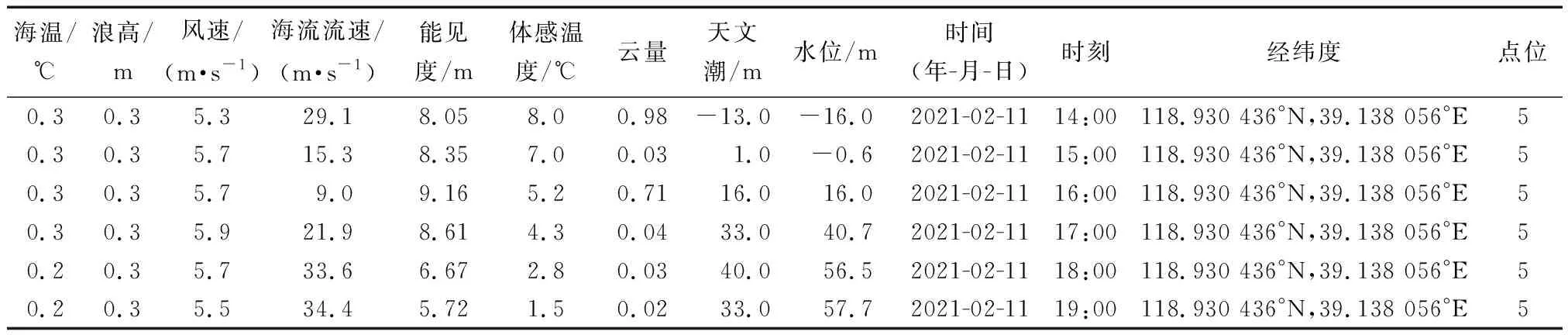
表1 海况数据表Table 1 Sea state data sheet

从表1的数据可以看出,该风电场的海况数据是间隔1 h进行记录更新,海况数据的要素包括海温(Sea_T)、浪高(WV_H)、风速(Win_S)、海流流速(SS)、能见度(VS)、体感温度(Som_T)、云量(CC)、天文潮(Ast_T)、水位(Wat_L)、年/月/日(YY/MM/DD)、时(Hour)、经纬度(LaL)、点位(Point)。

1.1.2 海况数据预处理

(1)数据清理。首先要对海况数据中重复、缺失的数据进行处理。使用线性插值技术,线性插值使用数据集中最后一个和第一个可用的平均值插补缺失值。公式为

(1)

式(1)中:f(x)为在位置x的估计值;f(x1)和f(x0)为已知数据点的对应值;x1和x0为已知数据点的位置。

(2)数据规约。数据归约则是通过降维删除不需要的属性来减少数据量,最大限度地减少数据丢失。其次,在尽可能保证数据信息完整性的同时,可以将已有数据降维到更低的维度,在实践中可以提高建模的效率[7]。

(3)数据变换。不同特征的数据维度可能不一致,如果对数据进行归一化,则数据值之间的差异可能非常大,如果不对数据进行处理,可能会影响数据分析的结果。因此,需要将数据按照一定的比例放缩,使其停留在特定区域进行综合分析。本文中采用最大-最小规范化方法将数据映射到[0 1]区间[8]。即

(2)

式(2)中:xnew为规范后的数据;x为原始数据;xmin和xmax分别为要将数据映射到的规范化范围的最小值和最大值。

1.2 随机森林

通过随机森林算法对冗余的数据进行剔除,只留下与海浪预测关联性大的特征,来避免因输入量过于繁杂带来的数据冗余问题[9]。图1所示为随机森林算法示意图。

图1 随机森林算法示意图Fig.1 Schematic diagram of the random forest algorithm

(3)

式(3)中:当0<σ<1时呈现正相关,-1<σ<0时呈现负相关。当σ的值无限接近1时,表明A和B之间呈现更高的相关性。

向量A和B分别表示各个数据集的向量值,任意一个数据集与另一个数据集之间的相关系数均由此计算。

图2所示为本研究中使用的数据集的特征相关热图,这些数据集以浪高作为分析目标。从图2可知,浪高与风速、海流流速、云量、天文潮和水位呈现正相关,因此当风速、海流流速、云量、天文潮以及水位较大(高)时,海平面会发生变化,海浪高度会随之变的更高且更加不稳定。浪高与海温、能见度和体感温度呈现负相关,考虑到当整体温度较高时且能见度较高时,天气相对比较晴朗,海平面更加稳定,海浪会变得更小、更加平稳[10]。

接下来进行特征重要性评估,在冗余的特征中选择出对预测结果影响最大的那几个特征,以此来缩减模型建立时的特征数。

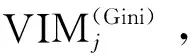
(2)第i棵树节点q的Gini指数计算公式为

(4)

式(4)中:pqc、pqc′为节点q中类别c、c′所占的比例。

节点q前后的Gini指数变化值为

(5)

假设特征XJ在决策树i中出现的节点为集合Q,那么XJ在第i棵树的重要性为

(6)

假设RF中共有I棵树,那么

(7)

最后,将重要性评分进行归一化处理,得到特征重要性评估结果,公式为

(8)

如图3可以看出,在海浪预测变量重要性度量[12]过程中,风速与海浪的关联最紧密。

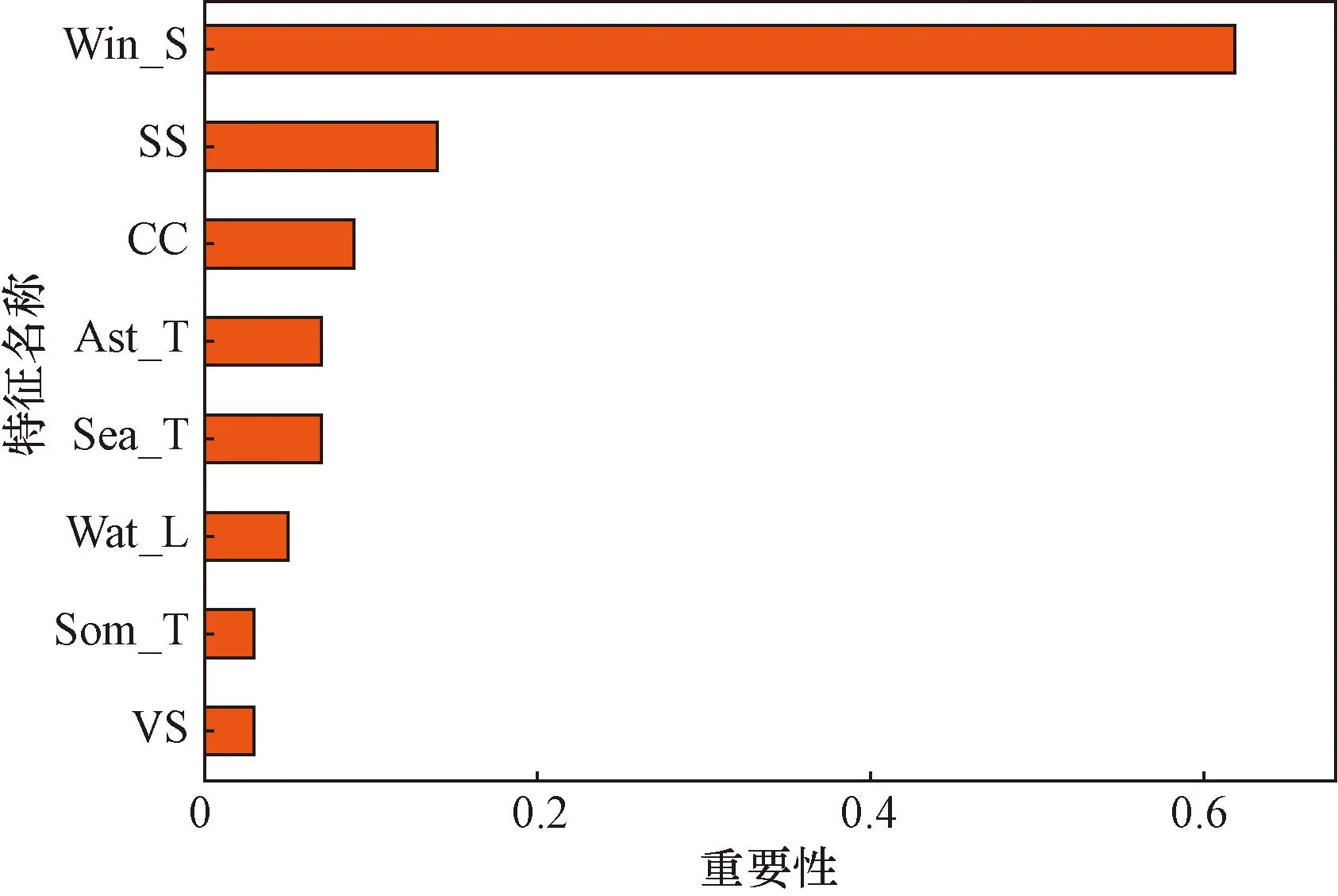
图3 随机森林特征选择结果Fig.3 Random forest feature selection results

1.3 数据预处理模型

1.3.1 变分模态分解(VMD)

VMD是一种非递归和自适应分解模型,用于处理非平稳信号的自适应分解[13]。该模型采用wiener滤波对相关参数进行初始化,得到K估计的中心角频率wk,然后使用交替乘法更新每个模态函数及其中心频率,并将每个模态解调到相关的频段,以最小化总估计带宽。公式为

(9)

式(9)中:δ(t)为单位冲激函数;{uk}={u1,u2,…,uK}和{ωk}={ω1,ω2,…,ωK}为K从固有模态函数(IMF)分解中获得的分量和中心频率。式(9)通过使用改进拉格朗日算子λ(t)和二次惩罚因子得到,即

L({uk},{ωk},λ)=

(10)

寻找变量受限的最优解,uk和ωk更新后得到

(11)

(12)

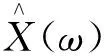
VMD模型的步骤如下:

(2)根据式(11)和式(12)更新uk、wk。

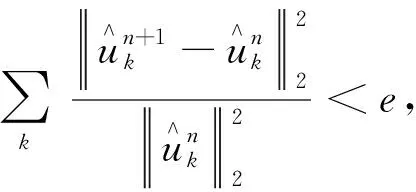
1.3.2 鲸鱼算法(WOA)

WOA作为一种新颖的智能算法,其核心是模拟座头鲸的狩猎行为。在WOA算法中,螺旋用于实现局部搜索,随机学习策略用于全局搜索。具体步骤如下。

(1)围捕猎物。座头鲸可以识别位置并包围猎物,在此算法中,离目标最近的单个鲸鱼的位置被设置为最佳位置。确定最佳位置后,其他鲸鱼会接近该位置。包围猎物的公式为

W(t+1)=W*(t)-AD

(13)

D=∣CW*(t)-W(t)∣

(14)

A=2ar1-a

(15)

C=2r2

(16)

(17)

式中:t为当前迭代;W*(t)为当前最佳位置向量;A、C为系数;r1和r2为0～1的随机数;a为一个0～2线性变化的量;Tmax为最大迭代次数。

(2)搜寻行为。座头鲸沿着螺旋路径走向猎物,模拟座头鲸狩猎行为的数学模型为

W(t+1)=W*(t)+Dpeblcos(2πl)

(18)

式(18)中:Dp=∣W*(t)-W(t)∣表示猎物到座头鲸的有向距离;b作为参数常量控制螺旋的形状;l为[-1,1]范围内的随机数。

此外,当座头鲸围绕猎物盘旋时,包围逐渐缩小。为了模拟这种行为,假设座头鲸选择了一个收缩的包络和螺旋模型,并有50%的概率更新它们的位置,因此开发了数学模型,即

(19)

式(19)中:p为[0,1]范围内的随机数。

(3)寻找猎物。座头鲸在寻找猎物时根据它们彼此之间的位置随机游动,这可以用以下数学模型表示,即

D=∣CWrand(t)-W(t)∣

(20)

W(t+1)=Wrand(t)-AD

(21)

式中:Wrand表示随机选择的鲸鱼位置,当|A|>1,鲸鱼被迫远离猎物,同时用随机生成的Wrand来寻找更合适的猎物。

1.3.3 基于WOA的VMD参数优化

使用WOA优化VMD参数的过程如图4所示[14]。首先初始化座头鲸的种群位置向量[K,α],以包络熵为适应度函数计算每头座头鲸的适应度,然后通过判断收敛因子的大小,选择迭代公式来更新迭代公式,得知满足终止条件,输出最优VMD参数。

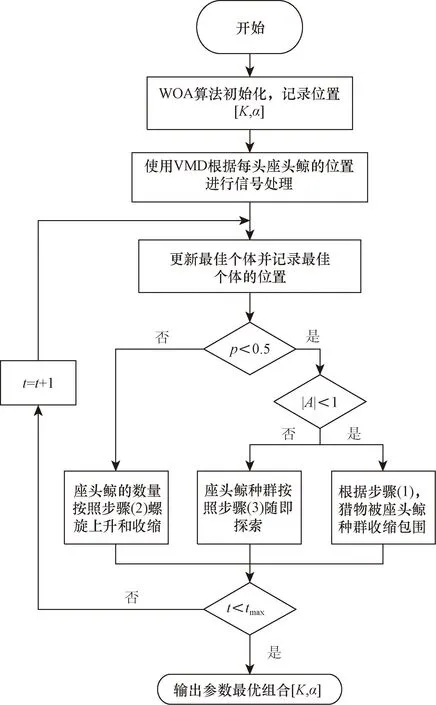
图4 基于WOA优化VMD参数流程图Fig.4 Flowchart of optimizing VMD parameters based on WOA

1.4 数据集成预测模型

1.4.1 双向门控循环单元(BiGRU)

图5为GRU的单元结构,其计算工作原理可表示为

图5 GRU单元结构Fig.5 Structure of the GRU unit

zt=σ(Wz[ht-1,xt])

(22)

rt=σ(Wr[ht-1,xt])

(23)

(24)

(25)

双向GRU由两个GRU组成:一个是正向的GRU模型,接受正向的输入;另一个是反向的GRU模型,学习反向的输入。BiGRU可以提高模型在后续预测问题中的性能,在任意时刻, 两个GRU的状态共同决定BiGRU的输出。BiGRU的具体结构如图6所示。

图6 双向GRU结构模型Fig.6 Bidirectional GRU structure model

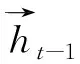
(26)

(27)

(28)

式中:wt、vt分别为正向权重参数和反向权重参数,bt为偏置参数。

1.4.2 注意力机制

在神经网络模型中,当输入大量的参数信息时会造成参数过载问题。而注意力机制恰好可以在复杂繁多的参数信息内找到最重要的信息,而对其他非重要的信息的注意力会下降,甚至可以有效地过滤掉一些无用信息,提高工作效率的同时保证了准确性。注意力机制主要应用在循环神经网络框架中隐藏状态矩阵Xi={X1,X2,…,XN}的生成过程中,计算表达式为

αi=p(z=i∣X,q)

=softmax[s(xi,q)]

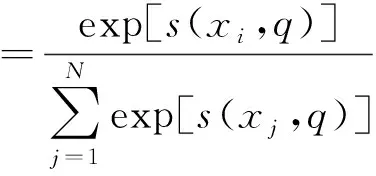
(29)

(30)

式中:Xi为第i时刻的隐藏状态信息;att(X,q)是注意力权重。

1.5 评估指标

为了比较不同模型的预测精度,采用均方根误差(root mean square error,RMSE)和平均绝对百分比误差(mean absolute percentage error, MAPE)两个评价指标对比RF-BiGRU、RF-BiGRU-Attention、RF-VMD-BiGRU-Attention、RF-WOA-VMD-BiGRU-Attention,通过分析结果判断RF-WOA-VMD-BiGRU-Attention模型预测准确。

(1)均方根误差RMSE数值越小代表预测误差越小,预测结果更加准确。计算公式为

(31)

(2)平均绝对百分比误差MAPE数值越小代表预测误差越小,预测结果更加准确。计算公式为

(32)

1.6 混合海浪预测模型

BiGRU网络可以有效地学习和训练波动的时间数据序列,从而提取时间特征。注意力机制的引入为特征分配了不同的权重,放大了重要信息的影响,提高模型效率。因此,该文提出一种引入注意力机制的BiGRU海浪高度预测模型。通过组合多种结构,学习原始数据的特性,获得更准确的预测结果。图7显示了有5个主要部分组成的模型结构:输入层、特征过滤层、特征分解、BiGRU层、注意力层和输出层。分解模块的结果作为下一层的输入,从所提出的特征中学习序列的时间变化模式,以实现预测功能。最后,通过输出层得到预测结果。

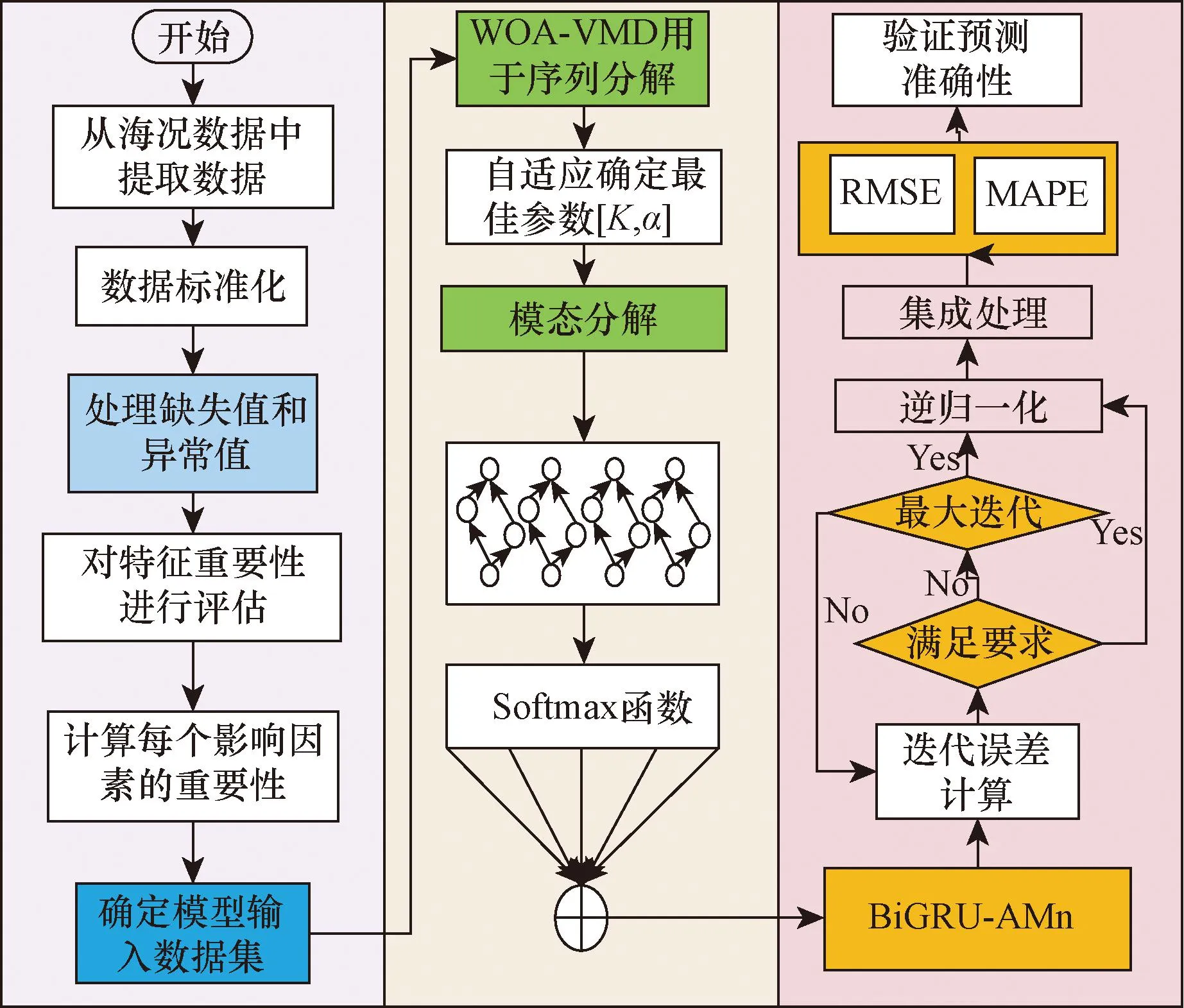
图7 基于RF-WOA-VMD-BiGRU-Attention的海浪预测模型框架Fig.7 Wave prediction model framework based on RF-WOA-VMD-BiGRU-Attention

2 实验分析

2.1 基于WOA-VMD的模型分解结果

为了验证基于RF-BiGRU海浪预测模型的卓越性,采用乐亭菩提岛风电场2020—2021两年的海况数据作为训练样本,预测样本为2022年上半年的观测数据,并用RF-BiGRU、RF-BiGRU-Attention、RF-VMD-BiGRU-Attention、RF-WOA-VMD-BiGRU-Attention模型作为对比试验。

为了进一步提高数据质量并消除噪声的影响,采用WOA-VMD对海浪序列进行分解。首先,鲸鱼的数量设置为10,最大迭代次数为50,变量数量为2,惩罚因子为[100, 2 000],K取值范围为[3,7]且仅包含整数。然后使用WOA优化VMD参数。

如图8所示为预测模型训练和测试迭代50次的损失函数曲线,当迭代次数达到8次时,损失函数趋于收敛,且损失值基本不再变化。图9为惩罚因子优化曲线,经过8次迭代进化后,得到的最优惩罚参数为100。从图10可以看出迭代后,本征模函数(intrinsic mode function,IMF)最佳数值为7。基于上述确定好的参数,对原始信号进行分解,得到的基于WOA-VMD的模态分解图如图11所示。

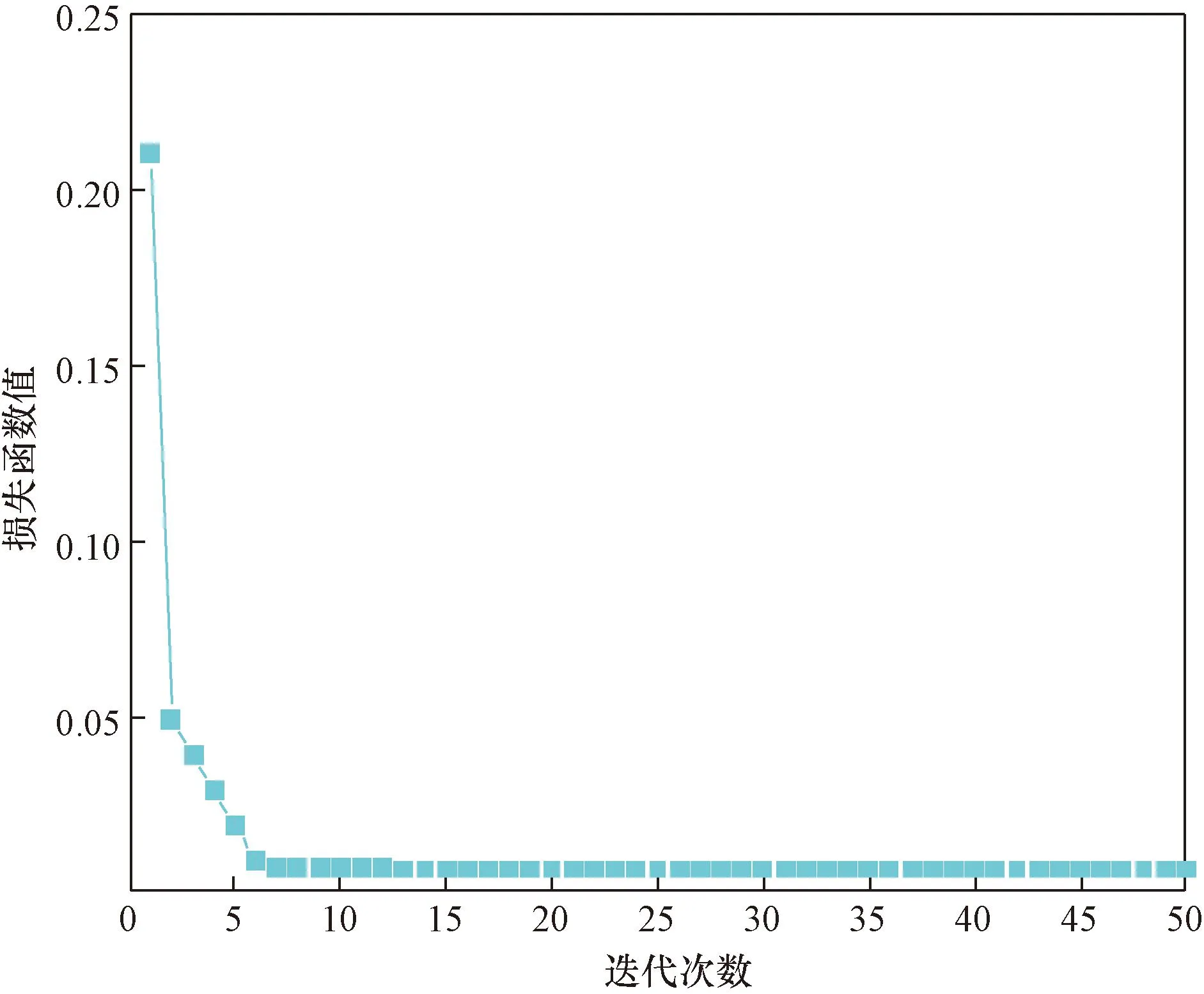
图8 损失函数曲线图Fig.8 Loss function graph

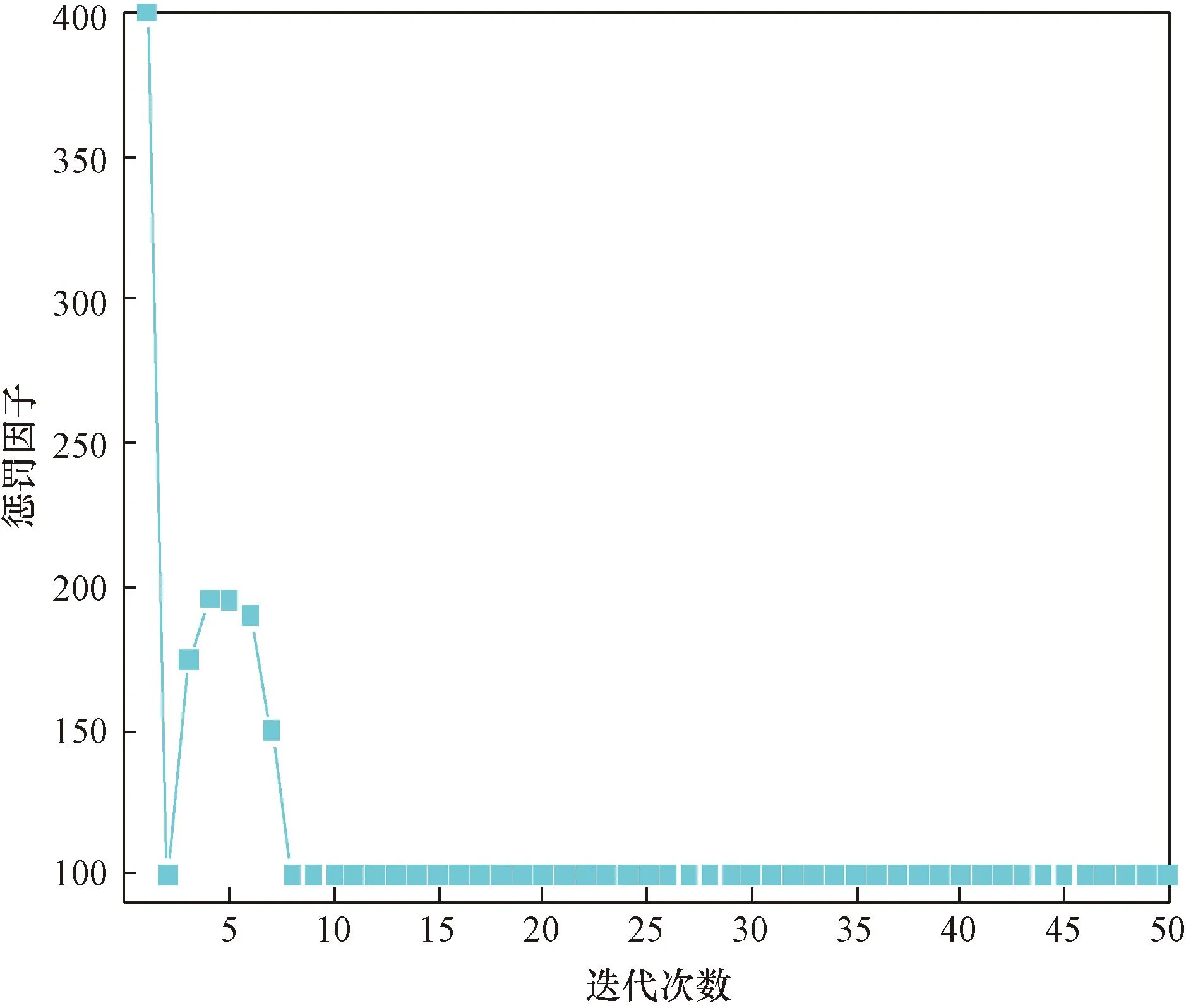
图9 惩罚因子优化曲线图Fig.9 Penalty factor optimization curve

图10 模态分解曲线图Fig.10 Modal decomposition curve

图11 基于WOA-VMD模态分解图Fig.11 Based on the WOA-VMD modal exploded view

2.2 基于RF-WOA-VMD-BiGRU-Attention模型浪高预测结果

由于文本海况数据量级过大,从数据集中随机选取连续5 d的数据进行预测,得到预测效果如图12所示。可以看出本文提出的RF-WOA-VMD-BiGRU-Attention模型具有良好的预测精度,在面对波动较大的海况数据时保持了良好的鲁棒性。本文提出的模型RMSE为0.555 7,MAPE为3.85%。

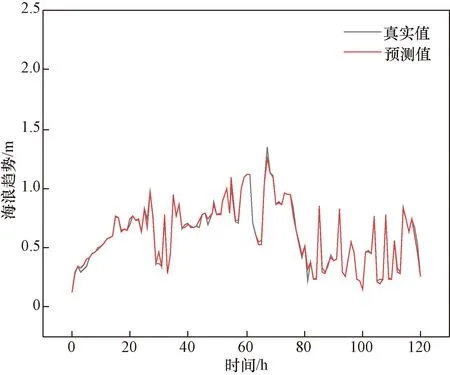
图12 RF-WOA-VMD-BiGRU-Attention模型预测效果图Fig.12 RF-WOA-VMD-BiGRU-Attention model prediction effect

2.3 多模型对比

为了评估所提出模型的优化效果,构建了另外3个模型来分别验证添加WOA、VMD和注意力机制的效果。如图13所示为多模型预测效果对比图。

为了精确地对比出不同预测模型的预测精度,表2为测试过程中RF-WOA-VMD-BiGRU-Attention、RF-VMD-BiGRU-Attention、RF-BiGRU-Attention、RF-BiGRU的RMSE、MAPE数值,通过对比RMSE和MAPE的值可以得出RF-WOA-VMD-BiGRU-Attention预测模型的预测精度更高。

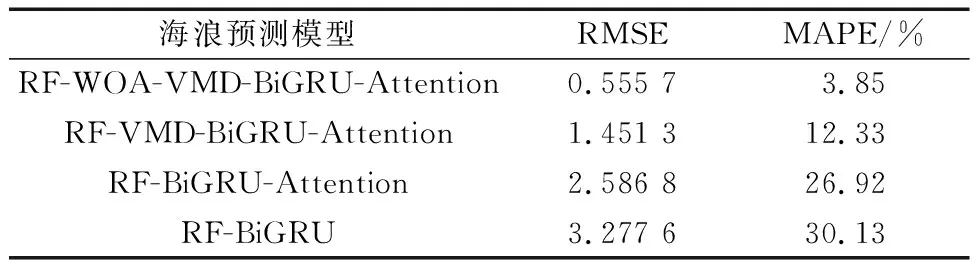
表2 各模型误差对比Table 2 Comparison of error between models

3 结论

本文搭建了RF-WOA-VMD-BiGRU-Attention模型,基于随机森林对输入特征进行筛选,利用WOA-VMD对模型的数据噪声进行分解,最后利用注意力机制进一步优化BiGRU来达到精准预测。以乐亭菩提岛风电场的海况数据为基础进行预测分析,实验结果表明,VMD可以有效地降低噪声,提高模型预测能力。VMD分解后RMSE和MAPE指数分别下降了43.90%和54.20%。采用WOA-VMD算法,得到VMD的最优关键参数,提高VMD的分解效果,应用WOA-VMD分解策略,RMSE和MAPE指数分别下降了78.52%和85.70%。注意力机制可以有效地聚集关键信息,消除冗余信息,引用注意力机制后,RMSE和MAPE指数分别下降了21.08%和10.65%。RF-WOA-VMD-BiGRU-Attention模型与其他模型相比,有效地降低了数据噪声的干扰,对于处理规模庞大的数据来说训练速度更快、结构更简单、处理长短序列性能更优越、内存消耗更少,能够更加准确地预测海浪高度。总体来说,本文提出了性能优良、泛化能力强的预测模型,但是海浪预测领域还是存在很多问题需要进一步研究。例如,没有考虑到风机尾流效应的影响,由于各个风电场的地理位置不同,导致海况数据的准确性也不同,预测结果也会有所不同,这也是将来我们进一步的研究方向。