“题组教学”在初中数学复习课中的应用
——以“全等三角形”大单元复习教学为例
●马玉洁
《义务教育数学课程标准(2022版)》指出,课程内容的选择要“符合学生的认知规律,帮助学生发展核心素养”;课程内容的组织要“对内容进行结构化整合,探索发展学生核心素养的路径”[1]。 “题组训练教学法”是中学数学复习课中的常用方法,这种复习方法以知识点为线索,以题组为载体,符合学生的认知特点,本文将详细探讨大单元视域下“题组训练”在初中数学复习课中的应用。
一、“题组训练” 在初中数学大单元复习课中的建构
大单元题组训练的方式是以一个单元或几个单元的知识点为背景,选取具有代表性、综合性和层次性的题目,将多个知识点融合在一起,形成不同难度的题组,以满足不同层次学生的需求。
(一)思想方法
1.转变思想
教师可以将复习课“讲—练—讲”的上课思路转变为“练—讲—练”或“练—议—练”,在课堂上充分发挥教师的引导性和学生的主体性。 题组设计的目的是让学生能够通过题组训练自主建构出知识网络,利用不同难度的由浅入深的题组去巩固知识、理解知识、应用知识、拓展知识。
2.转变方法
教师可以将“一题”“一练”转变为“一题”“多练”或“见题”“想法”,让学生在面对问题时有思路、有解决问题的办法。 做题的目的是通过做题找到解决此类问题的一般方法,因此教师要用“一题”让学生学会做一类题。
(二)选题原则
第一,系统性。 选取的题目要具有代表性,能够涵盖本单元的重要知识点和解题方法。
第二,应用性。选取的题目还应该具有一定的实际应用性,能够与学生的生活实际相结合,培养学生的数学应用能力。
第三,拓展性。 题目要具有一定的可拓展性,能够在原有知识点的基础上进行拓展和延伸, 培养学生的创新能力和解决问题的能力。
第四,层次性。 题目要具有一定的层次性,由易到难,满足不同层次学生的需求。
(三)讲解方法
在讲解题目时,应该注意以下几点:
一是注重引导。在讲解题目时,应该注重引导学生的思路和方法,帮助学生掌握解题技巧和解题思路。
二是突出重点。在讲解题目时,应该突出重点和难点,帮助学生掌握本单元的重要知识点和解题方法。
三是拓展延伸。在讲解题目时,可以适当拓展延伸相关知识,引入相关的知识点和解题技巧,帮助学生构建完整的知识体系。
(四)实施策略
1.利用开放型题组帮助学生构建大单元知识网络
大单元的复习课是对一个单元或几个单元知识的一个整体性复习和回顾, 学生也已经有一定的知识基础, 因此可以通过设计涵盖大单元知识的开放型题组帮助学生将所学知识进行整合, 进而构建大单元知识网络。
2.用新问题让学生产生串联旧知的新思考
复习课实际上就是把已学过的内容进行重现,用新的问题让学生将一个单元或几个单元的知识全都串联在一起,结合着小组交流活动使知识全面系统,让学生在回顾基础知识的同时收获基本活动经验。
3.用变式题组培养学生的创造力
初中阶段是培养学生创造性思维的关键时期,初中学生已经有了一定的基础知识和思维能力,也能够自主提出问题、寻找解决方法,并用创造性的思维来解决问题。利用变式题组让学生从一般到特殊,逐渐从具体的问题中抽象出共性和规律, 并运用到一类题中。
4.给予学生拓展性思考的时间
增强学生独立思考能力是培养学生数学解题能力和数学综合素养的重要方式。 在复习课中给予学生自主思考的时间可以让一部分学生去对本单元的知识内容、练习题目进行消化、整理,从而使知识内化;也可以让一部分学生进行提升训练,培养发散思维的同时激发学生数学学习的积极性。
二、“题组训练”在“全等三角形”大单元复习中的教学设计
下面以苏教版八年级上“全等三角形的复习”为例,展示大单元视域下借助“题组训练”开展课堂教学的思路和方法。
(一)【复习旧知,构建知识体系】——题组1

图1
1.感受全等
归纳:能________的图形叫做全等图形。全等图形________、________相同。 经历_______、_______、________前后两个图形全等。
2.运用全等
如图2,ΔABC≌ΔDEF,说一说,你能得到那些结论?
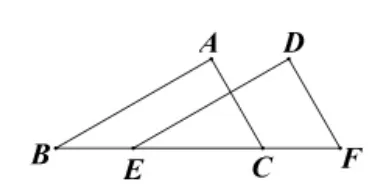
图2
归纳全等三角形的性质:
3.构造全等
如图3,已知AD平分∠BAC,要使△ABD≌△ACD。

图3
(1)根据“SAS”需添加条件()。
(2)根据“ASA”需添加条件()。
(3)根据“AAS”需添加条件()。
(4)如图4,已知AB=AC,BD=CD,求证:∠B=∠C。

图4
(5)如图4,已知AB=AC,∠B=∠C=90°,求证:BD=CD。
归纳全等三角形的判定方法。
【设计意图】建构有序的知识网络是复习课的首要任务。因此复习课引入阶段,要做到章节基础知识的覆盖[2]。 所以笔者以开放性问题的形式引入过渡,设计了由“已知三角形全等”得到“对应边相等、对应角相等”的性质;设计“由已知条件,证明三角形全等”帮助学生建构并回顾五种判定三角形全等的方法。
(二)【典型例题,覆盖重难点】——题组2
1.如图5,点E、F在CD上,且CF=DE,AE=BF,AE∥BF。

图5
求证:①△AEC≌△BFD;②你还能证得其他新的结论吗?
2.如图6:(1)利用尺规,作出∠CAB的平分线;(2)在∠CAB的平分线上任取一点,记为点P,如何在AB、AC上确定点D、E,使得△APD≌△APE,你有什么办法呢? 请在图中添加条件,并说明全等的依据。
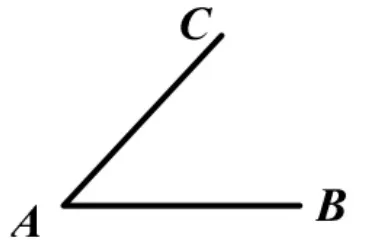
图6
【设计意图】新课标对学生尺规作图的能力新增了许多要求,尤其在作图的原理上提出了更高的要求,因此为帮助学生认识到尺规作图的重要性,笔者设计了第二个例题,让学生回顾用尺规作角平分线的过程,不仅复习巩固了基础知识,还加强知识之间的内在联系,满足大单元教学的要求,同时也能让学生更加充分地搭建本章的知识框架。
(三)【变式练习,巩固所学内容】——题组3
1.如图7,两个三角形是全等三角形,则∠a的度数是()
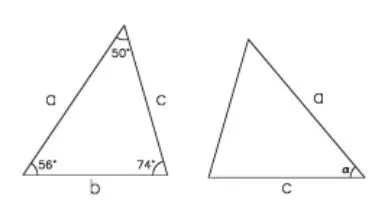
图7
A.50°B.58°C.60°D.72°
2.如图8,AB=AE,BC=ED,∠B=∠E,AF⊥CD,F为垂足,求证:CF=DF。

图8
3.如图9,锐角ΔABC中,AD⊥BC,BF⊥AC,若BE=AC,求∠ABC的度数。
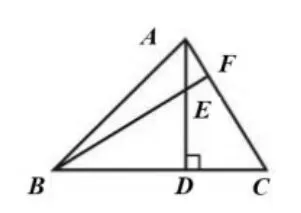
图9
【设计意图】本题组难度中等,重点在对知识点的应用与理解。 全等三角形的证明方法多种多样,学生需要能够根据题目条件选择合适的证明方法。同时,还需要注意一些常见的错误,如偷换概念、逻辑混乱等问题。 一些较复杂的全等三角形问题可能需要多个步骤才能解决,学生需要具备较高的逻辑推理能力和思维分析能力,以此培养学生的核心素养。
(四)【发散思维,合作探究】——题组4
1.如图10,△ABC是等腰直角三角形,∠C=90°,AE=BD,则△AED≌________;

图10
如图11,△ABC为正三角形,BD⊥BC,∠EDF=60°,则△BDE≌________。

图11
2.如图12,在△ABC中,AC=BC,D是AB上的一点,AE⊥CD于点E,BF⊥CD于点F,若CE=BF,AE=EF+BF.试判断AC与BC的位置关系,并说明理由。

图12
3.如图13,△ABC和△DCE都是等边三角形。
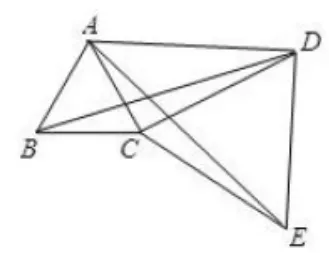
图13
(1)△BCD与△ACE是否全等? 若全等,加以证明;若不全等,请说明理由。
(2)若B、C、E三点不在一条直线上,∠ADC=30°,AD=3,CD=2,求BD的长。
(3)若B、C、E三点在一条直线上(如图14),且△ABC和△DCE的边长分别为1 和2,求△ACD的面积及AD的长。
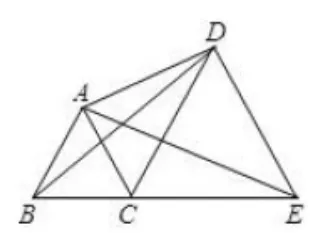
图14
【设计意图】本题组难度较大,是由全等三角形中的三个常见的模型组成。 由于学生之间存在个体差异,导致不同学生思维能力不同,因此为了让学生能够“吃得饱、吃得好”,笔者设计用此题组让学生进行合作探究,引导学生自主思考和解决问题,提高学生的思维能力和拓展探究能力。
实施“题组训练”时,应避免盲目“题海战术”或练习不够而导致的数学基本知识的遗漏, 教师要根据不同学生的个体差异设置高质量、有代表性、多层次、系统性强的题组,立足课本灵活性地选择教学资源,以达到培养数学核心素养的目的。

