大单元视角下数运算一致性的新实践
——以分数乘法教学为例
●王灵勇
一、探源:整体关联,吃透本质
2022版数学课程标准提出了“数运算的一致性”[1]重要理念。 数运算的一致性是指:无论整数、小数还是分数运算,本质上具备统一性,四则运算的意义、运算律、算理是一致的,都可以还原为计数单位的运算,算法上也具有内在的联系性。
(一)整体理解加与减的关联性
加法是运算的基础与核心,减法是加法的逆运算,如8+8=16,16-8-8=0;17+3=20,20-3-17=0。 整数、分数、小数加减运算,都是通过转化进行相同计数单位上的数字相加减。 加法是将若干个相同的部分或若干个不同的部分合成一个整体;减法是把一个整体分成若干个相同的部分或若干个不同的部分,如图1。
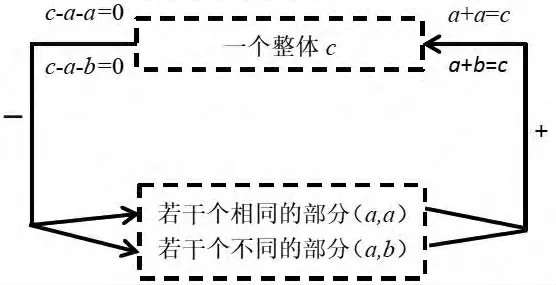
图1
(二)整体理解加与乘的关联性
整数、分数、小数的乘法算理是相通的,都是计数单位与计数单位相乘,计数单位上的数字与计数单位上的数字相乘。乘法是加法的简便运算,加法是将若干个相同的部分合成一个整体,乘法也是表示将若干个相同部分合为一个整体,如,3+3+3+3+3=15,5×3=15。 其结构关系如图2。
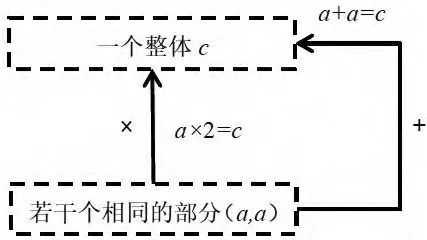
图2
(三)整体理解乘与除的关系
整数、分数、小数除法运算的算理是相通的,都是计数单位与计数单位相除,计数单位上的数字与计数单位上的数字相除。 乘除法教学应注重引导学生基于核心概念“计数单位”理解算法背后的算理,体会算理一致,乘法是将计数单位个数进行累加,除法是将计数单位个数进行均分,除法是乘法的逆运算,如5×3=15,15÷5=3。其结构关系如图3。
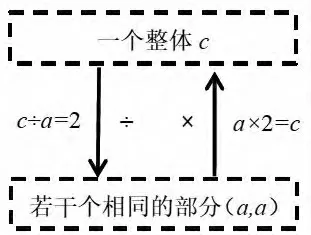
图3
(四)整体理解加减乘除四则运算的关系
整数、分数、小数的四则运算,本质上是一个整体,具有紧密的内在关联性。 加减乘除四则运算的算理都是基于运算定律和等式的基本性质,加减乘除四则运算的算法都需要立足于计数单位。要让学生真正感悟到加减乘除运算算理的一致性,教师对计数单位这一核心概念要特别引起重视。其结构关系如图4。
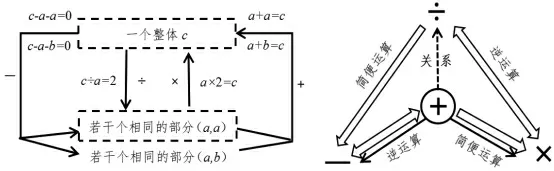
图4
二、寻根:测查学情,分析短板
计数单位是运算教学的核心概念,教师在开展运算教学时,不能将每节课孤立开,要充分研究运算间的内在联系。 教师研得充分,才能教得有结构,学生也才能学得有结构。 以北师大版五(下)数学教材“分数乘法”单元为例,学生在分数乘法的学习中,往往只记住法则,不理解算理。教师要以大单元的视角审视分数乘法的教学,将碎片化的知识建立起整体、系统、逻辑化的知识结构。 本文从一致性的视角,根据学情、教材,将分数乘法与整数乘法、小数乘法串联成知识群进行教学。在此基础上,对单元教学内容进行重新构架并设计相应的学习任务与教学活动。这样的教学使分数乘法的学习形成一个相互贯通的整体结构,为实现一致性的教学提供抓手,有助于学生理解数运算的一致性,提高运算能力和推理能力。
笔者通过对五年级学生的调研检测,发现学生对分数乘法意义理解片面,算理表征不明晰。 分数乘法算理具有一致性,学生思维进阶历程划分为不同的水平层次。 以整数乘分数为例,学生对“整数乘分数”的掌握分成以下不同水平:水平0,不能解决任何有关整数乘分数的问题;水平1,能用图示、举实例的方法理解分数乘法的一种意义;水平2,能正确理解分数乘法的两种意义。 通过对“你能举例说明6×的含义吗”的测试很能说明问题,具体情况如图5。
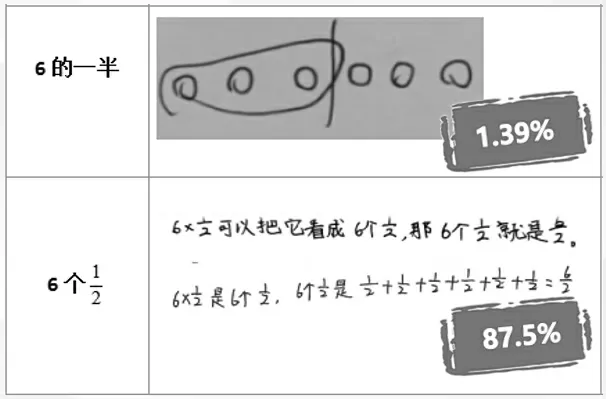
图5
通过测试发现,大多数学生对于整数乘分数的意义的理解停留在求相同分数的和这个最基础的水平。 处于水平2的学生能理解整数乘分数的两种意义,人数甚少。 因此,对理解分数乘整数求一个整数的几分之几的意义是认知难点。
三、扎根:探寻策略,优化路径
(一)注重数运算一致性的全局性理解
纵观北师大版教材,整数、分数、小数的运算,教材编排体系缺乏内在的一致性。如“分数乘法”,教材分为四个板块:分数乘整数(一);分数乘整数(二);分数乘分数;倒数。 学习分数乘整数,教材采用的是整数乘法的意义,如图6。

图6
到了分数乘分数的教学时算理前后并不一致,教材注重从乘法意义的角度来理解,,从分母乘分母得到新分母,分子乘分子得到新分子的运算中、看不出计数单位个数的累加过程。
整数、分数、小数虽然形式不同,但都共享十进位值制,运算的本质都是先拆分,然后进行计数单位个数的运算,有内在的一致性。分数单位的多变性其运算更复杂,因此,运算一致性理解的关键与难点都在分数。 分数乘法的核心目标是掌握分数乘整数和分数乘分数的计算方法,体会运算算理的一致性,基于此,笔者对原有的分数乘法教材体系作了适当调整。
第一课时“分数×整数”的教学,重点要帮助学生建立分数乘整数与整数乘法之间的联系。 算理和整数乘法相通,算法来自同分母分数的加法。学生通过迁移算法来解释算理, 初步感知乘法运算的一致性,分子乘整数其实就是在计算计数单位的个数,分母不变的道理是计数单位没发生变化。
对于“分数×整数”运算的另一种意义(求一个整数的几分之几),只有约1.39%的学生想到。 对于这个教学难点的突破,需要引导学生借助“倍”的经验,将6的表示为6的倍,以“倍”作为统领帮助学生感悟分数乘法的意义,其实就是整数乘法意义的扩展,这也是另外意义上的一致性。
将原“分数×分数”这一课时拆分成“分数单位×分数单位”和“分数×分数”两个课时,同时将原教材“约分”的教学内容后移,这样更加凸显新计数单位的产生以及对新计数单位个数累加过程的理解,接着增加一节计数单位的梳理课。 通过教学顺序的调整进一步引领学生探究分数乘法与整数、小数乘法算理一致性的过程:它们都是计数单位乘计数单位的个数。 单位分数相乘,实质上就是计数单位和计数单位相乘得到了一个新计数单位,这为后续的任意分数的乘法奠定了基础。 非单位分数相乘运算是基于计数单位的运算, 如是计数单位相乘,产生了新的分数单位,c×d计数单位上的数字相乘,是新的分数单位的个数。 从而将分数乘法与整数、小数乘法算理的一致性打通。
(二)践行数运算一致性的结构化路径
通过重新架构,“分数乘法”一致性教学的新授内容主要分为分数乘整数、分数单位乘分数单位、分数乘分数3个课时。 以下为分数乘法第一课时“理解分数与整数相乘的意义及算法”的主要学习路径重构:
在分数乘整数教学中与整数乘法相勾连,设计任务群驱动学习,通过知识迁移理解含义。
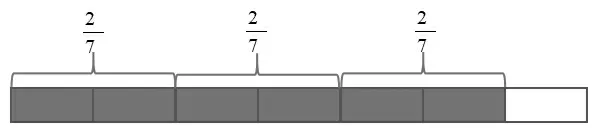
图7

图8
重构后的学习路径更能体现分数乘法算理的一致性。 各任务拾级而上,层层推进,每一个活动都紧紧围绕运算分数单位的个数实现一致性。

