基于双向热膨胀流的MEMS陀螺敏感机理分析

马炫霖,朴林华,佟嘉程,刘珺宇

(北京信息科技大学 北京市传感器重点实验室,北京 100101)

0 引言

微型热气体惯性传感器是一种新颖的惯性传感器,利用热气体(如空气、N2、SF6等)代替传统的固体质量块作为敏感元件。热膨胀流陀螺是一种以哥氏效应为基础的新型微机电系统(MEMS)惯性传感器,可以克服微型热对流式流体陀螺加热电阻和热敏电阻不在同一水平面的缺点,通过推拉式的气体流动,提高了热流陀螺灵敏度,避免了无重力场情况下热对流陀螺无法工作的缺点,与传统的微型振动陀螺仪相比,热膨胀流陀螺具有成本低,体积小,质量轻,抗冲击和振动能力强等优点,易于实现智能化与数字化[1-2]。微型热膨胀流陀螺仪的灵敏度相对较低,主要原因是热气体的等效质量和运动速度均小于固体质量块。因此,提高热膨胀流陀螺仪的灵敏度是亟待突破的关键技术之一。

2012年,Leung教授首次提出热膨胀流陀螺的结构和敏感机理[3]。此结构包含2个加热器及1对温度传感器,通过2个加热器交替加热产生“推拉式”的热膨胀流,通过热敏电阻来检测由科氏力引起的温度差,从而检测z轴角速度。2017年,常洪龙教授设计了一种基于双向热膨胀流的微机械三轴气体惯性传感器。该传感器由4对加热器和四对热敏电阻构成,形成一个含有4个测量单元的“交叉”网络[4]。2018年,Kock教授提出了一种新型无惯性质量块单轴气体热膨胀流陀螺仪,该陀螺仪由2个加热器(H1、H2)和2个温度探测器(TD1、TD2)组成,加热器和温度探测器悬在氮化硅制成的桥上,通过检测温差来测量z轴角速度[5]。2019年,Luo教授通过提出一种采用二维热膨胀流陀螺仪(μTEG)模型来预测传感器性能的方法,研究了薄膜参数、加热器间距等因素对传感器灵敏度的影响[6]。2022年,郭教授提出了一种新型三轴陀螺仪,解决了加工难及z轴抗高过载能力未知等问题。它包括两个独立的部分,这两部分相互嵌套以进一步减小结构体积,同时避免了耦合问题[7]。然而由于这些热膨胀流陀螺加热器和热敏电阻排列位置的原因,加热器加热时部分热气流流失,从而导致其温差较小及灵敏度较低的问题。目前大部分热膨胀陀螺均采用两组加热器交叉加热或单热源加热,这将使线加速度与旋转角速度间产生耦合效应,并导致腔体内流体受力不均匀,无法实现高速流动等问题。此外,现有陀螺仿真都是利用二维模型对其陀螺性能和敏感机理进行仿真,与三维仿真计算结果相比存在误差较大。因此,有必要研究一种高灵敏度、能有效抑制交叉耦合的热流体陀螺,且对其性能预测和敏感机理验证进行三维模拟。本文提出一种新型的基于双向热膨胀流陀螺结构,并通过COMSOL Multiphysics构建其有限元模型,分析在有无角速度时温度场和等温线的变化情况,试图揭示该新型结构陀螺的敏感机理。

1 结构原理

基于双向热膨胀流的陀螺结构主要包括密封盖板和敏感层。盖板和敏感层构成腔体从而密封气体,并为气体的热流动提供空间。图1为MEMS陀螺的三维结构示意图。该陀螺包含6个加热电阻(HL1、HR1、HL2、HR2、HL3、HR3)(下文统称为H1、H2、H3)和4个热敏电阻(TDL1、TDR1、TDL2、TDR2)(L、R分别表示位于左、右两侧的敏感元件),从而形成3组左右对称的加热器进行交替加热及两组检测电阻进行温差测量。基底层的主要材料是单晶硅,并采用硅表面加工技术进行制作。加热电阻和热敏电阻材料为铬、铂、金。溅射铬是为了增加铂的粘附性,采用金作为金属电极。

图1 MEMS陀螺的结构示意图

图2为基于双向热膨胀流的MEMS陀螺工作原理示意图。两组加热器H1、H3与H2通过周期性的方波信号交替加热,加热器周围的气体体积受热膨胀,进而产生推挽式的热膨胀气体流[8]。两组热敏电阻TDL1、TDR1、TDL2、TDR2阻值相同,可以检测出热气体的温度变化。假设热敏电阻TDL1、TDL2敏感到的平均温度为T1,热敏电阻TDR1、TDR2敏感到的平均温度为T2,则两热敏电阻间的温度差ΔT为

图2 MEMS陀螺的工作原理示意图

ΔT=T1-T2

(1)

由图2(a)可知,当z轴无角速度(ωz=0)时,H1、H3通电加热时,H1、H3周围的气体受热膨胀,H2周围的气体冷却收缩,热流由H1、H3的两侧流向中间的H2。由图2(b)可知,H2通电加热时,H2周围的气体受热膨胀,H1、H3周围的气体冷却收缩,热流由中间的H2向两侧的H1、H3流动,此时左右检测电阻TDL1、TDR1和TDL2、TDR2上的温度相同,温度差ΔT=0。当z轴有顺时针角速度输入(ωz>0)时,热源将会在垂直于x轴的方向产生哥氏力,使得热膨胀流发生偏转,导致热敏电阻检测对产生温差。由图2(c)可知,热敏电阻TDR1周围的温度升高,T1T2,温度差ΔT>0。角速度越大,热气体所受的哥氏力越大,使更多的热流流向热敏电阻,使ΔT增大。因此,角速度与热敏电阻的温度差成正比,即ΔT∝ωz。

温差在铂电阻上体现为阻值的变化,设初始电阻阻值为R0,热敏电阻TDL1、TDR1和惠斯通电桥输出电压关系[9]为

RTDL1=R0(1+αT1)

(2)

RTDR1=R0(1+αT2)

(3)

ΔR=RTDL1-RTDR1=αR0(T1-T2)=
αR0ΔT

(4)

(5)

同理可推出U6为

(6)

式中:Rref为参考电阻;RTDL1,RTDR1分别为热敏电阻TDL1、TDR1的阻值;U5,U6分别为经过一次差分放大后的输出电压;α为铂电阻的温度系数;A为该差分放大器放大倍数。电路输出电压Vout为

ΔT

(7)

图3为MEMS陀螺输出电路。两对热敏电阻通过惠斯通电桥输出后进入一级差分放大电路进行处理,最后经过二级差分放大电路输出。

图3 MEMS陀螺输出电路

基于双向热膨胀流陀螺是一种角速度传感器,其工作原理是传感器受到角速度作用时,热气流在科里奥利力(Coriolis force)的作用下发生偏转,y方向的3组加热器产生的热气流沿相反方向到达对应热敏电阻,形成相反的加热效应,使热敏电阻产生温差,通过将温度变化转化为热敏电阻的阻值变化,最后转化为输出电压的变化,通过测量电压的大小,进而测出角速度,实现z轴角速度的精确测量[10]。

2 有限元计算

为降低传感器的制作成本,缩短研发周期,提高传感器的性能,流片前需对传感器的敏感机理及影响传感器性能的诸多因素进行大量的理论研究[11]。本文采用有限元方法,利用COMSOL Multiphysics建立三维模型,并对双向热膨胀流陀螺敏感元件内的温度场和等温线的变化情况进行了计算。

2.1 物理模型

基于双向热膨胀流的MEMS陀螺的热敏元件的三维物理模型如图4所示。图中,下腔室对应基底中的倒梯形凹槽,上腔室对应空腔,空腔内填充气体。本模型通过忽略加热器和热敏电阻的结构对气体温度场和等温线的影响,以此保证其结构不对气体的流动及温度分布产生阻碍[9]。

图4 MEMS陀螺结构的三维模型

施加在加热器上的周期性方波信号可以通过软件自带的方波函数和解析函数组合得到[8],对热源H1、H3加载此方波,如图5所示。对热源H2加载与图5(a)反相的方波,以此构成两组交替加热的热源。方波周期为0.10 s,方波的占空比为50%,加热器功率为70 mW。三维COMSOL模型尺寸如表1所示。表中,l×w×h表示长×宽×高。

表1 MEMS陀螺三维COMSOL模型尺寸

图5 热源1加载方波

2.2 数学模型

MEMS热膨胀流陀螺腔体内部的气体流动和温度变化过程符合质量守恒方程、惯量守恒方程、热能守恒方程和状态方程[9]为

(8)

(9)

(10)

P=ρRT

(11)

式中:ρ为腔体内气体密度;R为理想气体常数。

将空气作为腔体内部的工作气体,其相关参数如表2所示。表中,M为气体平均摩尔质量,T0为腔体内初始温度,PAir为腔体内气体压强。

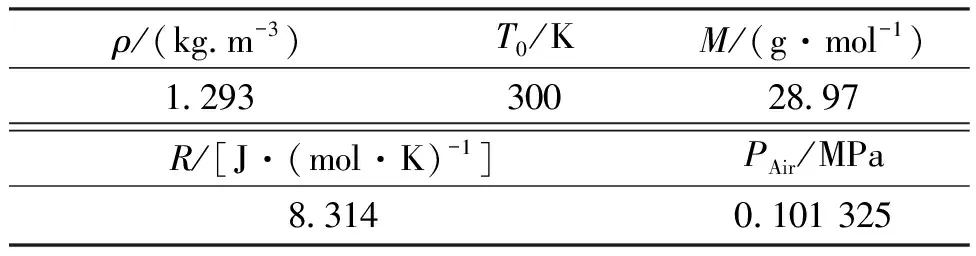
表2 三维COMSOL模型工作气体相关参数

2.3 有限元法求解

在确立物理模型和数学模型后,利用三大守恒公式,再加上边界条件,如滑移边界条件及入口边界条件[12]。利用COMSOL软件对陀螺的敏感元件在有无角速度时温度场的变化情况进行有限元分析和计算。其求解过程如下:

1) 建立有限元模型。

2) 模型参数设置。

3) 物理场选择。

4) 划分网格。

5) 计算[11]。

3 计算、结果及讨论

本文中加热器功率为70 mW,交替加热时间为0.05 s,加热器H1、H2的温度呈周期性“推挽式”的交替变化。随着时间的增加,加热器的最高温度不断升高,但两加热器间的温度差趋于稳定,平均温度差约为80 K。两加热器间的温度差变化曲线如图6所示。

图6 两加热源加热产生的温差

图7(a)为0.3 s未施加角速度(ωz=0)时基于双向热膨胀流陀螺的加热状态。图7(b)为0.35 s未施加角速度(ωz=0)时MEMS陀螺的加热状态。由图可看出,在未施加角速度的情况下,0.3 s时,对加热器H1、H3进行加热,热气流分布均匀,左、右两对电阻温差为0。在0.35 s时H2加热器加热,热气流分布均匀,上下电阻温差为0。图8为加热器H1、H3与H2分别加热时陀螺密封腔体内等温线的分布情况。

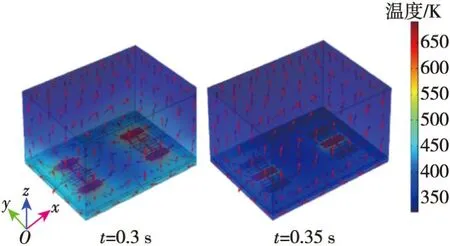
图7 ωz=0时,H1、H3与H2加热时MEMS陀螺温度场的运动情况

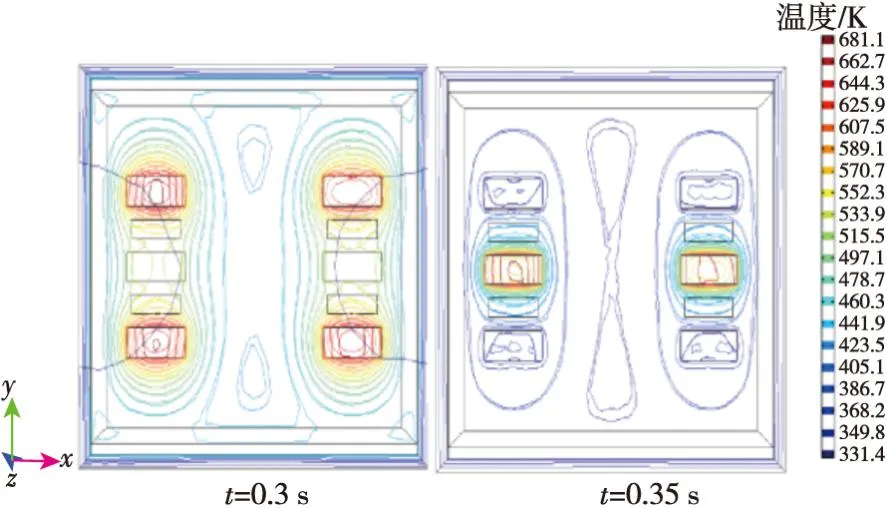
图8 ωz=0时,H1、H3与H2加热时MEMS陀螺等温线的分布情况(顶视图)

在ωz=25 rad/s时,温度场和等温线的计算结果如图9、10所示。当H1、H3加热器加热,热气流在科里奥利力作用下产生偏转,由于陀螺旋转方向为顺时针,故加热器H1产生的热膨胀流流向热敏电阻TDR1较多,使热敏电阻TDR1周围气体的温度大于TDL1周围气体的温度,故ΔT<0;同理,在t=1.20 s时,加热器H2加热,使热敏电阻TDL1周围气体的温度大于TDR1周围气体的温度,故ΔT>0。该结论验证了MEMS热膨胀流陀螺仪敏感机理,是灵敏度计算的基础[11]。

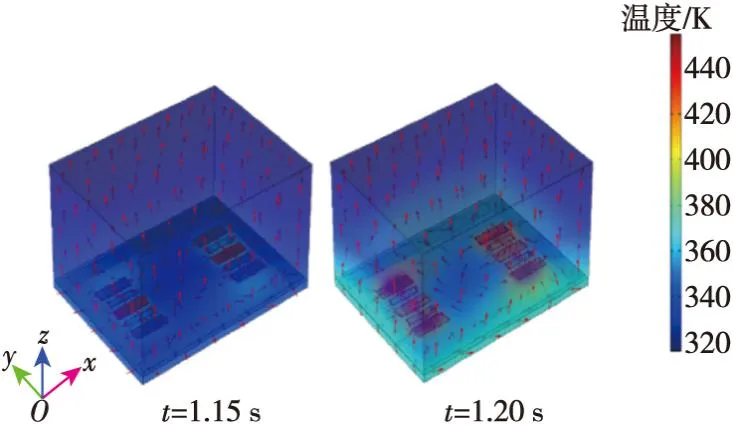
图9 ωz=25rad/s时,H1、H3与H2加热时MEMS陀螺温度场的运动情况

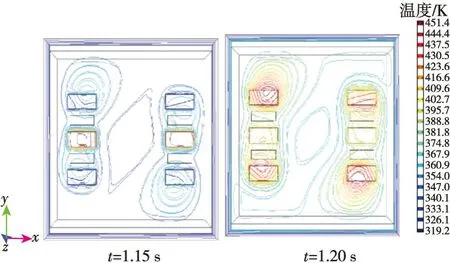
图10 ωz=25 rad/s时,H1、H3与H2加热时MEMS陀螺等温线的分布情况(顶视图)

图11为MEMS陀螺的温度灵敏度曲线。通过COMSOL有限元分析可知,在输入角速度ωz为-30 ～30 rad/s时,ΔT斜率为正。为使仿真更精准,最小二乘法的拟合效果更佳,选择输入角速度为-25～25 rad/s。MEMS陀螺的温度灵敏度拟合曲线如图12所示。

图11 MEMS陀螺的温度灵敏度曲线

图12 MEMS陀螺的温度灵敏度拟合曲线

设MEMS陀螺的输入角速度与热敏电阻的平均温度差关系为

(12)

Uout=cΔT+d

(13)

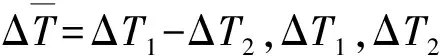
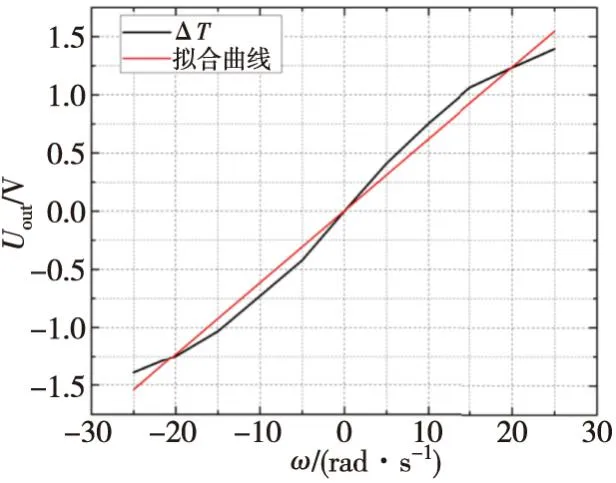
图13 MEMS陀螺的输入-输出特性曲线

Uout=0.064ω+0.039

(14)

综上所述,本文所提出的基于双向热膨胀流的MEMS陀螺在输入角速度ω为-25～25 rad/s,输入功率为70 mW时,灵敏度为0.064 V·(rad/s)-1,非线性度为6.855%。

4 结束语

本文提出一种基于双向热膨胀流的MEMS陀螺结构,并对其原理进行了介绍。该热陀螺由3组交替加热的加热器及4个热敏电阻构成,采用异步驱动的方式对加热器加热。在角速度产生时,角速度会使加热器所产生的热膨胀流在哥式力的作用下发生偏转,导致两对热敏电阻的温度变化,通过对其温差的转换,将其输出为电压的变化,实现z轴角速度的准确测量。采用有限元方法,利用COMSOL Multiphysics建立三维模型,对双向热膨胀流陀螺敏感元件内的温度进行了计算。计算结果表明, MEMS陀螺具有陀螺效应,输入角速度为-25～25 rad/s,陀螺的温度灵敏度为1.577 K·(rad/s)-1,灵敏度为0.064 V·(rad/s)-1,非线性度为6.855%。与现有的微型热气体陀螺仪相比,该陀螺不仅有抗冲击能力强,结构简单,成本低及功耗低等优点,还因其独特的结构优势和异步驱动方式,可以实现更高的输出灵敏度和更好地抑制交叉耦合的效果,可用于电子设备、航天和医学仪器等领域。