基于改进量子粒子群优化算法的机器人逆运动学求解
陈卓凡 周坤 秦菲菲 王斌锐
摘要 :针对工业机器人在逆运动学求解过程中存在的位姿奇异、解不唯一、求解精度低等问题,提出了一种改进量子粒子群算法。首先,利用D-H参数法建立机器人运动学模型,以机械臂末端最小位姿误差为主要优化目标,加入运动前后关节角变化最小、行程平稳连续的约束条件,设计了目标函数;其次,通过采用Levy飞行策略改进粒子更新方式、非线性地动态调整收缩膨胀因子、采用变权重方法计算最优平均位置等方法设计了一种改进量子粒子群优化(IQPSO)算法;然后,模拟单点位姿和连续轨迹两种不同的求解情况进行三种算法(IQPSO、APSO、QPSO)的仿真对比实验,结果表明IQPSO算法具有收敛速度快、求解精度高等优点;最后,将IQPSO算法用于机械臂本体进行实物验证,实验结果表明IQPSO算法求解出的插值点所组成的轨迹连续且平滑,进一步证明了该算法应用于实际运动控制中的稳定性和可行性。
关键词 :工业机器人;逆运动学求解;目标函数;改进量子粒子群优化算法
中图分类号 :TP242.2
DOI:10.3969/j.issn.1004-132X.2024.02.014
开放科学(资源服务)标识码(OSID):
Inverse Kinematics Solution of Robots Based on IQPSO Algorithm
CHEN Zhuofan ZHOU Kun QIN Feifei WANG Binrui
School of Mechanical and Electrical Engineering,China Jiliang University,Hangzhou,310018
Abstract : Aiming at the problems of singular pose, non-unique solution and low solution precision in the inverse kinematics solution processes of general robots, an improved quantum particle swarm optimization algorithm was proposed. Firstly, the robot kinematics model was established by using the D-H parameter method, and the minimum pose errors at the end of the manipulators were the main optimization goal, and the constraints of the minimum joint angle changes before and after the movement and the smooth and continuous stroke were added, and the objective function was designed. Secondly, an IQPSO algorithm was designed by using the Levy flight strategy to improve the particle update method, nonlinear dynamic adjust the shrinkage and expansion factors, and using the variable weight method to calculate the optimal average position. Then, the simulation and comparison experiments of three algorithms(IQPSO,APSO,QPSO) were carried out by simulating two different solutions of single point pose and continuous trajectory. The results show that the IQPSO algorithm has the advantages of fast convergence speed and high solution accuracy; finally, the IQPSO algorithm was used in the body of the robot arm for physical verification. The results show that the trajectory composed of interpolation points obtained by the IQPSO algorithm is continuous and smooth, which further proves the stability and feasibility of the algorithm in practical motion control.
Key words : industrial robot; inverse kinematics solution; objective function; improved quantum particle swarm optimization(IQPSO) algorithm
0 引言
工业机器人作为工业自动化领域的一个重要组成部分,已经被大量应用于电子、医疗、物流、交通制造、军工等行业 [1] 。工业机器人的逆运动学求解旨在依据给定的末端位姿信息计算出机械臂各关节所对应的角度值。由于描述机器人结构的数学模型具有非线性的特点,因此整个求解过程可以看作是求解一个多变量、强耦合下的高维非线性方程组,求解过程较为复杂且可能会出现多组解 [2] ,对于逆解如何取优也是一个研究难点。目前有关逆运动学的算法主要分为解析法、数值法、智能算法等。对满足Piper 准则的机器人可以使用解析法进行求解 [3] 。这种解法利用代数几何以及投影的方法可以获得闭合形式的逆运动学解,但是由于计算过程繁琐导致整体运算量偏大,且受限于机器人构型,普适性差 [4] 。数值法通常采用迭代求解,对于迭代初值选取较为敏感且迭代过程中雅可比矩阵会出现奇异导致无解。智能算法不受构型限制,它通过设立一个合适的适应函数将逆解问题转化为一个智能优化问题。目前应用较为广泛的智能算法包括人工神经网络 [5] 、遗传算法(GA) [6] 、粒子群优化(PSO)算法 [7] 等。神经网络算法的准确性更多地取决于网络的结构,且需要大量已知样本进行训练;遗传算法在单个染色体上使用交叉操作然后相互比较,共享效率较低;粒子群优化算法直觀高效,易于实现,执行效率高,可以避免繁琐的数学公式推导,比较适合作为机器人逆运动学的求解方法 [7] 。但是由于PSO算法在运算初期需设定的参数(惯性权重 ω,学习因子c 1、c 2) 太多,不利于找到最佳的优化参数。近年来有许多学者针对标准PSO算法存在的问题提出了改进方法,SANCAKTAR等 [8] 提出一种自适应的粒子群优化算法,并将其用于求解三自由度机械臂的逆运动学问题;姜涛等 [9] 提出引入收缩学习因子提高算法收敛能力的方法;DU等 [10] 提出了三种关于惯性权重的非线性调整方法,证明了相比较线性调整惯性权重,非线性调整方法有更好的优化效果。
然而PSO算法终究不是一个符合全局收敛准则的全局收敛算法,其全局搜索能力非常依靠对粒子速度上限的设定。针对此,孙俊 [11] 提出了一种具有量子行为的粒子群优化(QPSO) 算法,相比较传统粒子群算法,该算法取消了粒子的速度属性,参数更少,收敛速度更快。TIAN等 [12] 用选定的基准函数去测试QPSO算法性能后也验证了该算法的优越性。在分析讨论QPSO算法的收敛性时,SUN等 [13] 分析了算法迭代公式的参数选择对搜索能力的影响,并提出了可以增强全局搜索能力有效避免局部优化的方法;TURGUT等 [14] 提出在量子粒子群中引入不同的混沌映射从而达到提高算法鲁棒性的方法;ZHANG等 [15] 在初始化量子位置信息时引入高斯分布的变异算子以增加种群的多样性。
然而上述方法的改进思路都集中在优化种群初始化过程、预防算法早熟等方面,对算法更新准则中局部吸引子和搜索范围这两个直接影响位置更新速度的因素研究不够具体。因此本文在该领域先前的研究基础上针对上述问题提出了一种改进的量子粒子群优化(IQPSO)算法。首先,对本文的研究对象——六轴工业机器人机械臂进行运动学建模与分析,并根据优化目标建立合适的适应度函数;其次,介绍粒子群算法和量子粒子群算法的相关原理和联系,并在QPSO算法基础上引入Levy飞行策略改进局部吸引子更新方式,采用非线性方法动态调整收缩膨胀因子,采用变权重方法计算平均最优位置,从而优化粒子的搜索范围;然后,通过仿真实验模拟工作空间中任意單点位姿和连续轨迹两种不同的求解情况,将本文所述改进算法与加入混沌映射和高斯分布的QPSO算法、自适应粒子群算法进行对比求解分析,证明IQPSO算法的优越性;最后在六轴工业机器人平台上应用IQPSO算法进行实际运动过程中的点位求解,验证该算法在真实工作中的可行性和可靠性。
1 六轴工业机器人运动学建模与分析
1.1 机器人运动学建模
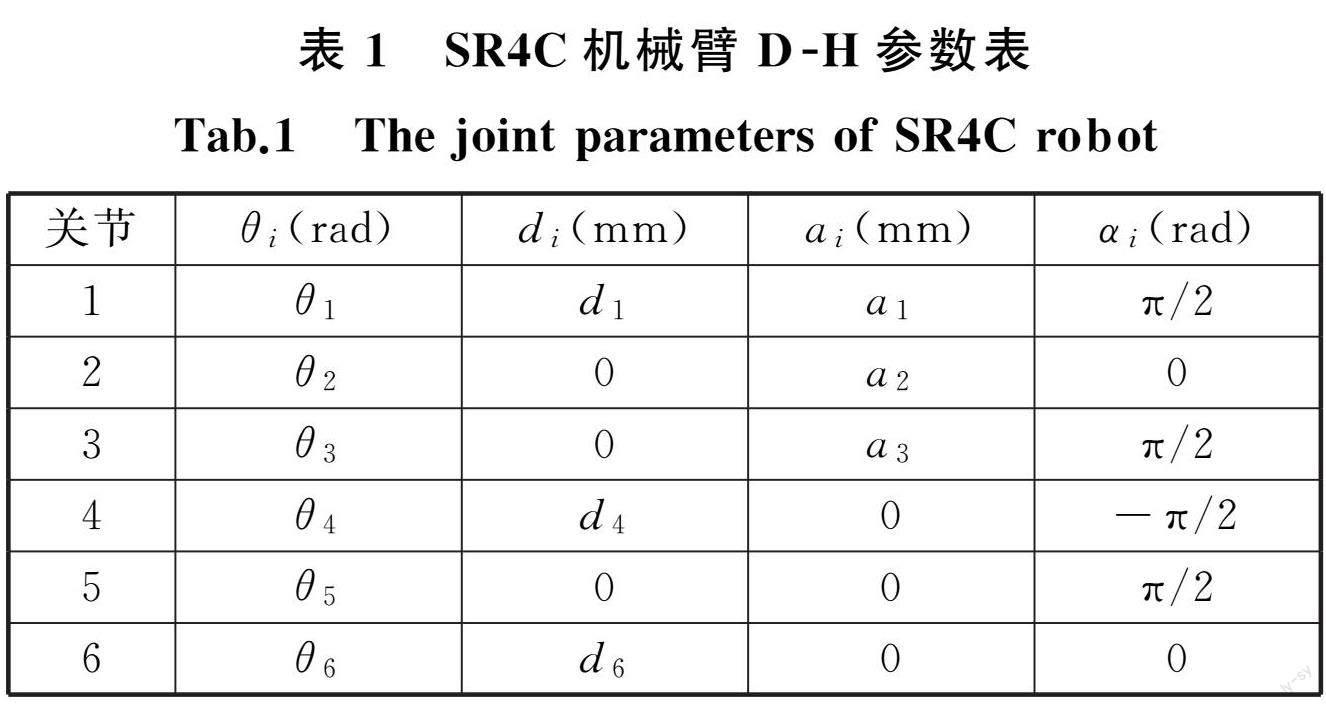
本文所采用的六自由度新松SR4C机械臂符合Pieper准则,根据表1给出的各关节信息,采用改进D-H参数法建立连杆坐标系,如图1所示。
其中,θ i、α i、a i、d i分别表示每一个连杆的关节角、扭转角、连杆长度以及连杆偏移。根据 SR4C 机械臂实际参数,将各轴的连杆偏移和连杆长度选取如下:
d 1=330 mm ,d 2=0,d 3=0, d 4=310 mm , d 5=0,d 6=70 mm ,a 1=40 mm ,a 2=315 mm ,a 3=70 mm ,a 4=0,a 5=0,a 6=0。
因此表示相邻坐标系间位姿变换关系的齐次矩阵如下:
i-1 i T =
cos θ i - sin θ i cos α i sin θ i sin α i a i cos θ i sin θ i cos θ i cos α i - cos θ i sin α i a i sin θ i 0 sin α i cos α i d i 0 0 0 1 (1)
将表1中的 D-H 参数代入式(1)后,可以得到各个关节的齐次变换矩阵。随后依据正运动学表达式,将6个齐次变换矩阵从左到右相乘就可以得到机器人末端相对于基坐标系的位姿矩阵 0 T 6:
0 T 6= T 1 T 2 T 3 T 4 T 5 T 6=
n x o x a x p x n y o y a y p y n z o z a z p z 0 0 0 1 = R 3×3 P 0 1 (2)
式中, R 3×3 为末端执行器相对于基坐标系的姿态变换矩阵; P 为末端执行器相对于基坐标系的位置变换矢量。
1.2 目标函数的建立
智能优化算法旨在将机器人逆运动学求解的问题转换为优化控制的问题来解决,因此需要设立一个合适的优化目标函数。给定机械臂末端执行器的期望位姿矩阵为
T des = R 3×3, des P des 0 1 (3)
将初始关节角度θ i代入式(2)后,可以得到当前关节角所对应的位姿矩阵:
T cur = R 3×3, cur P cur 0 1 (4)
为了让机械臂的末端执行器达到期望位姿,需要使得式(3)和式(4)满足:
Δ=‖ T cur - T des ‖=0 (5)
满足式(5)的关节角度即为正确的逆运动学解。同时满足条件的关节角度的边界条件设置为
θ l i≤θ i≤θ u i i=1,2,…,6 (6)
式中,θ l i、θ u i分别为第i个关节所对应的关节上限和关节下限。
由于式(5)同时涉及到了姿态的9个变量和位置的3个变量,方程组的构成较为复杂,因此本文将其分解为一个关于姿态误差的函数Δ 1和一个关于位置误差的函数Δ 2:
Δ 1=‖ Δ R 3×3 ‖=‖ R 3×3, cur - R 3×3, des ‖ (7)
Δ 2=‖ Δ P ‖=‖ P cur - P des ‖ (8)
实际工程应用中常会出现多组解的问题,在逆解取优时应以机器人各关节角θ i变化最小作为取优的依据,此时运动前后机器人姿态变化最小可保证运动行程的平稳连续。 假设在运动过程中,当前点P s 经求逆后对应的角度为θ s ,i (i= 1,2,…,6),目标点P r 所對应的角度为θ r ,i (i=1, 2,…,6), 则各关节角度的变化函数为
F(θ)=∑ 6 i=1 |θ r ,i -θ s ,i | (9)
综上,可以将逆解问题转化为一个以位姿误差最小、各关节运动前后角度变化最小、运行稳定的多目标约束下的优化问题,目标函数如下:
min φ(θ)= min (Δ 1,Δ 2,F(θ)) (10)
式中,F(θ)为运行平稳目标。
由于式(10)涉及到了两个优化目标,包含三个子项,属于一个多目标优化问题,因此本文采用目前使用较为广泛的线性加权法,用三个不同的权重系数将式(10)的各项线性组合,转换为综合优化的方式,即
φ(θ)=μΔ 1+λΔ 2+γF(θ) (11)
由式(7)可以看出姿态误差函数是正弦余弦函数的组合,其参数单位为弧度;由式(8)可以看出位置误差函数以欧氏距离差表示,其参数单位为毫米;由式(9)可以看出关节变化函数以前后角度差表示,其参数单位为弧度。经实验后发现,三个子项并不处于同一量纲,因此需要设立权重系数μ、λ、γ对各子项进行归一化处理,选取不同的参数协调各子项对目标函数收敛速度的影响,避免因数量级的问题而导致某种误差指标变化过小而被忽略。具体的系数设置根据机器人本体的参数值确定。
2 改进的量子粒子群优化算法
2.1 基本粒子群算法原理
PSO 是一种基于种群搜索的自适应进化算法,其基本思想在于通过群体中个体之间的合作和信息共享来寻找到最优解。假设在N维空间内,由M个粒子组成的一个粒子群都以一定的速度在此空间内飞行搜索,设其中一个粒子m所处位置为 x m=(x m,1 ,x m,2 ,…,x m,N ),当前粒子m的飞行速度为 v m=(v m,1 ,v m,2 ,…,v m,N );粒子的个体最优预测位置为 p best =(p m,1 ,p m.2 ,…,p m,N ),粒子种群的全局最优预测位置为 g best =(g 1,g 2,…,g N)。标准 PSO 算法的表达式即粒子的飞行速度和位置更新如下:
v m,n (t+1)=ωv m,n (t)+c 1r 1(p m,n (t)-x m,n (t))+
c 2r 2(g m(t)-x m,n (t)) (12)
x m,n (t+1)=x m,n (t)+v m,n (t+1) (13)
m=1,2,…,M n=1,2,…,N
式中,ω为惯性权重;c 1、c 2为学习因子,也称个体加速度系数和群体加速度系数;r 1、r 2为[0,1]内均匀分布的随机值。
2.2 具有量子行为的粒子群算法
标准的粒子群优化算法可以解决多峰、高维的控制优化问题,但是当变量个数增多且维数变大后,计算量大大增加且稳定性降低,很容易陷入局部最优 [7] 。对于求解六轴工业机器人的θ i(i=1,2,…,6),该算法并不完全满足稳定性和精度的要求,理论上来说并不能称为一种全局性算法,因此孙俊 [11] 将量子行为引入粒子群算法,提出一种全新的量子粒子群优化算法。该算法在进行优化迭代时摈弃了式(12)所示的速度更新,转而只更新粒子的位置信息。为保证量子粒子群算法收敛,每一个粒子必须收敛到自身的局部吸引子(又称势阱中心),吸引子的定义如下:
p m,n (t+1)=φp m,n (t)+(1-φ)g best ,n (t) (14)
φ∈[0,1]
式中,p m,n 为当次迭代时第m个粒子个体最优位置的第n维,它影响粒子每次迭代过程的进化收敛趋势;g best ,n 为整个粒子群体最优位置的第n维。
QPSO 算法引入了量子态粒子行为,用一个波函数Ψ(x,t)描述粒子的位置状态 [12] ,随后求解薛定谔方程获得粒子的概率密度函数Q和概率分布函数D,确定粒子出现在工作空间中某处的概率:
Q(x m,n (t+1))= 1 L m,n (t) exp (-2|p m,n (t)-
x m,n (t+1)|/L m,n (t))
D(x m,n (t+1))= exp (-2|p m,n (t)-
x m,n (t+1)|/L i,j (t)) (15)
L m,n (t)=2a|W n(t)-x m,n (t)| (16)
W n(t)= 1 M ∑ M m=1 p m,n (17)
式中,L m,n (t)為粒子间的特征长度,用来确定粒子的搜索范围;W n(t)为 QPSO 算法中定义的全新参数,表示第t次迭代时所有粒子的平均最优位置;a为收缩膨胀因子。
至此粒子在空间中的具体位置可通过蒙特卡罗逆变换方法获得 [16] ,位置更新方程如下:
x m,n (t+1)=p m,n (t)± 1 2 L m,n (t) ln (1/u) (18)
其中,u表示0~1均匀分布的随机数,当u>0.5 时“±”取“+”,当u<0.5 时“±”取“-”。
由式(18)可知,因子a成为了计算过程中唯一需要控制调整的参数,而且先前的粒子移动不再影响粒子下一次的位置更新,使其具有更高的随机性,提高了群体智能程度,理论上可以在搜索空间内找到最优解。因此本文基于这些特性,改进优化 QPSO算法中粒子的搜索范围从而更好地协调算法全局和局部的搜索能力,保证算法拥有更好的收敛速度和求解精度,然后运用改进的QPSO算法对机器人进行逆运动学求解。
2.3 改进的量子粒子群优化算法
由式(18)可知, QPSO 算法的位置更新过程中粒子局部吸引子p m,n (t)和特征长度L m,n (t)这两个关键要素起到了很大的作用,p m,n (t)决定了粒子种群在之后迭代过程中的进化方向,L m,n (t)用来确定粒子的搜索范围,并且由收缩膨胀因子和平均最优位置这两个因素共同决定。本文基于上述特征,针对 QPSO 算法进行三方面的改进,使算法可以根据各粒子运行过程中的实际情况不断优化调整搜索幅度和范围,提高 QPSO 算法的准确性和鲁棒性,加快整体收敛,防止算法陷入局部最优,进一步协调好算法的局部搜索和全局搜索能力。
2.3.1 引入 Levy 飞行策略
由式(14)可以看出,粒子的势阱中心由当前粒子的个体最优和当前群体的历史最优决定。然而当算法在迭代过程中历史最优值g best 陷入局部最优时,由于计算公式中g best 与p m,n 存在线性组合关系,p m,n 也会因此陷入局部最优导致算法过早收敛。本文为解决此类问题引入 Levy 飞行策略进行改进。据文献[17-18]记载,目前针对许多智能优化算法如粒子群优化算法、蚁群算法的研究中,都会选择利用 Levy 分布确定迭代步长的随机游走过程,然后通过粒子较大的跳跃在搜索空间中进行更有效的搜索,从而可以在一定程度上摆脱算法的局部最小值,提高搜索能力。因此在势阱中心的计算中引入 Levy 飞行策略,当种群进化方向陷入局部最优时重新分布粒子位置,改善 QPSO 算法提早收敛的劣势。
Levy飞行是一类非高斯随机过程,其随机游走服从Levy稳定分布。当将Levy飞行策略引入到量子粒子群算法中时,需首先定义一个符合Levy 分布的步长因子s:
s=rand(size(D))Levy(k)~ u |v| 1 k (19)
σ u=( Γ(1+k) sin ( π k 2 ) Γ( (1+k)k 2 )2 (k-1) 2 ) 1 k σ v=1
式中的参数u和v分别都满足于正态分布,即u~ N (0,σ 2 u),v~ N (0,σ 2 v)。函数rand(size(D)) 表示该粒子种群所有维度下的随机数,表示生成的随机向量与满足 levy 分布中采样得到的向量进行逐元素相乘,最终得到维度为D的步长因子s。σ u定义式中的Γ是根据式(19)获得的D维标准伽马函数的值;k为[1,3]的随机数。
将定义好的步长因子s放入势阱中心的计算公式中,有
p m,n (t+1)=s|x m,n -(φp m,n (t)+
(1-φ)g best ,n (t))| (20)
至此,将式(14)和式(20)作为粒子局部吸引子的两种更新方式,可根据不同情况进行选择。在算法初始化过程中事先给每个粒子设置一个界限值l lim 并初始化跟踪值t trial 为0。若每次迭代生成的新粒子对应的适应度值并未得到改进,则跟踪值递增一次;若迭代出的新粒子对应的适应度值相比前一次有所改善,则置t trial =0。当出现t trial >l lim 时,代表算法已陷入局部最优情况, 适应度值过早收敛,此时采取 Levy 飞行方法,根据式(20)重新计算局部吸引子位置进行后续迭代。
2.3.2 非线性调整收缩膨胀因子
通过重新设计调整收缩膨胀因子a的计算公式,可以在每一次迭代过程中都充分考虑并结合粒子最优位置和平均位置的距离差,达到动态调整粒子搜索范围的效果,提高算法的收敛能力,避免陷入局部最优。对于如何调整收缩膨胀因子a的问题,本文引入了相似性的概念 [19] 。定义粒子m和粒子n之间的相似度如下:
S(m,n)=1-( d(m,n) d max ) 2 (21)
式中,d(m,n)为两粒子间的欧氏距离差;d max 为空间粒子间的最大距离。
由式(21)可知,当d(m,n)→0时,S(m,n)→ 1;当d(m,n)→1时,S(m,n)→0。距离越近相似度越高,反之相似度越低。
根据这个特性就可根据粒子的局部吸引子位置和粒子群体的全局最优位置的距离差来选择调整收缩膨胀因子。设定当前粒子局部吸引子位置p m,n 和全局最优位置g best ,n 间的相似度为S(p m,n ,g best ,n ),当S(p m,n ,g best ,n )→0时,说明此时的距离差最大,该粒子距离群体的全局最优位置最远,所以在下一次迭代时需要脱离现在的搜索区域,加强全局搜索的能力,因此收缩膨胀因子值也随之增大;当S(p m,n ,g best ,n )→1时,该粒子距离全局最优最为接近,无需跳出且只需在当前的小区域内加大局部搜索的能力即可搜索到最优解,所以收缩膨胀因子值随之减小。
当S(p m,n ,g best ,n )(0,1)时,收缩膨胀因子的更新公式如下:
a m=a min +(a max -a min )·
S(p m,n ,g best ,n ) t max -t t max (22)
本文设定a max =0.9,a min =0.3。将经过式(22)调整过的收缩膨胀因子应用于式(16),即可达到非线性动态调整搜索范围的目的。
2.3.3 變权重方法计算平均最优位置
QPSO 算法中引入的平均最优位置W n(t)只是将种群内所有粒子的个体历史最优值相加求平均计算。这样的计算方法自动认定每个粒子的个体最优对最终的平均最优值所起到的作用一致,如下式所示:
W n(t)=( 1 M ∑ M m=1 p m,1 (t), 1 M ∑ M m=1 p m,2 (t),…,
1 M ∑ M m=1 p m,N (t)) (23)
然而在实际计算时,每个粒子的适应度值都不尽相同,适应度值越大说明该粒子在种群中就越重要,将这些粒子的个体最优都统一计算求取平均最优值显得不够准确,所以本文将粒子根据适应度值的大小降序排列,然后采用文献[20-21]中的方法为排序好的粒子分配不同大小的权重系数。整体遵循适应度值越大,在整体收敛逼近最优解的过程中起到的作用越大,其权重系数也应越大的准则。调整后的平均最优位置计算如下:
W n(t)=( 1 M ∑ M m=1 α m,1 p m,1 (t), 1 M ∑ M m=1 α m,2 p m,2 (t),…,
1 M ∑ M m=1 α m,N p m,N (t)) (24)
式中,α m,n 为权重系数,本文中根据不同粒子的适应度大小将权重系数从1.5到0.5线性变化。
2.4 改进量子粒子群优化算法的求解流程
针对求解量子粒子群的势阱中心p m,n 时可能会陷入局部最优的问题,采用 Levy 飞行策略使其跳出局部最小值,避免算法提早收敛;针对原特征长度L m,n 并未充分考虑全局搜索和局部搜索协同的问题,制定了非线性动态调整收缩膨胀因子和变权重方法计算平均最优位置等改进方式提高了 QPSO 算法的准确性和鲁棒性。改进量子粒子群算法的流程如图2所示。具体步骤如下:
(1)初始化种群大小、维数、最大迭代次数等种群参数,设定粒子迭代的起始位置,极限值l lim 和跟踪值t trial 。
(2)根据式(11)所示目标函数求取当前过程的适应度值,从而确定个体最优p m,n 和全局最优g best ,n 。
(3)进入循环,计算得出各粒子的局部吸 引子。
(4)利用上文所述的变权重方法计算平均最优位置W n,并根据当前点与历史最优点的距离差动态调整收缩膨胀因子,计算出特征长度L m,n 。
(5)根据 IQPSO 算法的迭代方程得出粒子的最新位置,计算其适应度值判断是否有所优化。
(6)若有优化,表明粒子处于正常搜索状态,置跟踪值t trial 为0,跳转到步骤(8);若没有优化,则表明粒子可能会陷入局部最优区域,跟踪值自增1并转去判断是否超过极限值l lim 。
(7)当t trial (8)通过分析新粒子的适应度值确定个体最优p m,n 和全局最优g best ,n 。 (9)判断是否满足终止条件,若满足则输出最 终的g best ,若不满足则返回步骤(3)进入下一次迭代。 3 仿真验证与分析 3.1 对单点进行改进算法的求解验证 按照2.4节所描述的改进QPSO算法流程,对图1所示的SR4C机械臂模型进行逆运动学求解验证。仿真实验环境为MATLAB 2018b,Win10 Intel(R) Core(TM) i5-7300Q CPU @ 2.50 GHz。 为避免实验的偶然性,在机器人工作空间内随机选定5组期望位姿和初始关节位置,并分别用引入收缩因子 [9] 的自适应PSO算法(将其记为APSO) 、采用混沌映射和高斯分布的QPSO算法 [15] (将其记为QPSO)、本文所述的改进QPSO算法(将其记为IQPSO)进行求解,然后对比分析。5组初始关节位置和期望位姿矢量见表2、表3。 为方便统计,表2、表3中的各数据取小数点后四位。表2中的关节角度用弧度值表示;表3中的 RPY 角度ψ r 、θ r 、φ r 表示姿态矢量,用弧度制表示;p x、p y、p z表示位置矢量。 算法的目标函数采用式(11)所示的形式,对式(11)中三个不同的权重系数进行归一化处理,用于平衡各子项的数量级。根据 SR4C机器人的D-H 参数以及参照表2、表3列出的关节角、位置、姿态数据,确定姿态误差、关节角变化函数的数量级在10 0,位置误差的数量级在10 3。为便于计算,同时结合调试经验选取姿态误差的权值系数μ=1作为基准;关节角度变化的数量级单位与姿态误差保持一致,选择 γ=μ=1;位置误差的单位为毫米,数量级为10 3,确定λ=1×10 -3 。 设置IQPSO算法的最大迭代次数为400,种群粒子数量为50;APSO算法的参数设定和实现参考文献[9]。将3种算法分别用于求解表3所列的5组期望位姿,将每种算法所收敛的最终适应度值统计在表4中,为便于记录将表中数据统一保留4位有效数字。 由表4可以看出,求解不同的期望位姿,本文所述的 IQPSO 算法的收斂效果基本都比其他两种方法更好,从中可以看出该算法的求解效率高,同时也具有较高的求解稳定性。 为方便直观地看出各种算法在迭代过程中的表现,本文将每个期望位姿的适应度值相加除以测试的组数,取对数处理后生成的平均适应度值的收敛曲线如图3所示。 由图3可以看出:IQPSO算法在整体求解过程中,其收敛速度和求解精度要优于QPSO和APSO这两种改进粒子群算法的收敛速度和求解精度,同时相比较标准QPSO算法而言,IQPSO算法在更早的迭代过程中就已经以一个相对较快的加速度进行收敛,在迭代超过40次后再以一个相对较慢的速度进行局部的仔细搜索直到收敛到最优值。整个过程相比较其他算法而言,更好地平衡了粒子的全局搜索能力和局部搜索能力,一定程度上证明了2.3节所述观点。 为了更加清晰地评价各种算法在求解精度上的差异,统计各种算法在经过5组期望点求解后的实际位姿T cur 相对于期望位姿T des 的误差,将位置误差和姿态误差的均值( Δ R+ Δ P)/2作为对比分析的指标,其中位置误差值 Δ R和姿态误差值 Δ P遵循下式: Δ R= ∑ 3 m=1 ∑ 3 n=1 (r mn -r mn, des ) 2 (25) Δ P= (p x-p x, des ) 2+(p y-p y, des ) 2+(p z-p z, des ) 2 (26) 经数据处理后将误差的平均值、最大值、最小值统计在表5中。 由表5可以看出:IQPSO算法在对单点的求解过程中所产在的误差最小,证明了该算法在应用于机器人逆运动学求解问题时所体现出的优越性。此外分别运用这三种算法对5组期望位姿进行逆运动学求解时,IQPSO算法的平均运算时间为0.12791s,QPSO算法的平均运算时间为 0.1506 s, APSO算法的平均运算时间为0.2156 s,从中可以看出IQPSO具有更快的求解速度,耗时相比较其他算法来说也有一定的优势,验证了算法整体在迭代过程中具有更快的处理速度。 3.2 对连续轨迹进行改进算法的求解验证 本节将算法用于求解连续轨迹上的各个插值点,对比这几种算法在求解连续轨迹时的适应度值收敛效果。同时通过计算轨迹上各个插值点的姿态误差和位置误差,分析比较各种算法在针对连续轨迹求解问题上所体现出的求解精度优劣性。 在机器人工作空间内随机选取4个目标点A、B、C、D,然后采用 MATLAB 工具箱中的插值函数进行每两点间插值,插值50个点共形成2条连续轨迹AB、CD。再将几种算法分别应用于轨迹AB和CD进行实验。图4是选定的两条期望轨迹,图5则是各种算法求解出的各插值点所组成的跟踪轨迹。两条轨迹端点A、B、C、D的位姿信息记录在表6中。 将各种算法对两条轨迹上的插值点独立重复求解5次后,计算并绘制出来两条轨迹上的插值点的平均位置误差和平均姿态误差变化的对比如图6、图7所示。 同时根据生成的位置误差和姿态误差曲线,分别计算两条轨迹共100个插值点所产生误差的最大值、最小值、平均值和标准差,其中最大最小值体现了求解算法的性能;平均值体现了算法求解的精度;标准差则体现出算法的稳定性和鲁棒性。表7统计了位置误差的各项指标,表8统计了姿态误差的各项指标。 分析图6、图7得知,几种算法在对轨迹上各插值点进行求解时都会存在一些控制精度上的波动,但是整体保持在10 -5 数量级以下;本文所述IQPSO算法求解出的各插值点相较于期望的各点来说, 位置误差和姿态误差都比QPSO算法和APSO算法求解的误差小,求解精度有了很大的提高, 这一点在表7、表8的最大最小值比较中也得以体现。同时IQPSO算法在求解中兼顾了精度要求和稳定性要求,误差的平均值和标准差相比较其他两种算法也具有明显的优势。进一步证明了本文2.3节所述观点。 4 实验验证 为验证算法的可行性,将算法应用于团队现有的实验平台,在新松SR4C机械臂实体上进行运动学求解的实物验证。现有实验平台由主控器、 4 kg 新松SR4C机械臂、控制柜(内含6个 Panasonic 驱动器)、示教器组成,如图8所示,机器人本体有6个关节电机,通过动力线和编码器信号线与控制器内的驱动器相连。各个驱动器之间采用串联方式并由第一个驱动器通过EtherCAT与主控器建立通信。 进行实物实验时,首先需要在示教器上输入示教点,编写示教运动指令;然后主控器通过TCP/IP通信接收到示教指令并进行解析;再根据解析结果调用插补运算部分中的规划函数和逆运动学求解算法,生成组成轨迹的各个插补点以及对应的关节角数据,控制机械臂各关节电机完成相应运动。 为充分验证IQPSO算法在机械臂实际工作时的效果,本文分别针对同一平面下的定姿态轨迹和曲面变姿态轨迹两种不同情况进行实物实验,分析验证算法的合理性和实用性。 4.1 平面轨迹实验 本节实验选定一条双扭线轨迹作为实验对象。首先在示教器上输入相应的点位信息和运动指令,示教指令如图9所示。为记录下机械臂运行的轨迹,自制了一个连接件将喷枪固定在机械臂末端,在白纸上进行喷绘实验。然后主控器接收并解析图9所示的用户程序,根据“MOVL”的解析结果调用所对应的速度规划算法生成对应的插补点,再利用本文所研究的IQPSO算法对各个插补点进行逆运动学求解,生成每个点位所需的关节角数据,最后点位数据经由主控器发送给各从站驱动器,在完成关节数据转换为编码器值后,各从站驱动器控制本体六个电机完成相应的轨迹运动。利用图9所示用户示教程序所绘制的轨迹如图10所示。 然后按照图11所示先在机械臂末端安装靶球并采用Leica-AT403型号的激光跟踪仪对机械臂所走轨迹进行跟踪测试, 跟踪轨迹如图12所示。轨迹上各点对应关节角变化如图13所示。 从图10、图12中可以看出,机械臂末端根据IQPSO算法解算出的点位所组成的轨迹段连续平滑且并未出现明显的突变情况,说明算法在计算各插值点过程中未出现无解或超出关节限位的情况,证明了算法在实际应用时的可靠性。 从图13中可以看出,各关节角的变化曲线都呈现平滑且连续的特征,证明了利用IQPSO算法求解的各插值点所对应的关节角满足运动平稳性要求。 4.2 曲面轨迹实验 本节实验中同时改变机械臂的姿态和位置信息,让末端执行器在一个平滑半球的曲面上运行,以此验证IQPSO算法在求解曲面轨迹上各个变姿态点位时的效果。在操作台上固定一个半球面,让机械臂在半球面上进行变姿态的曲面画圆作业。 绘制变姿态圆时,示教调用步骤与4.1节所述一致,实际运行的轨迹如图14所示。激光跟踪仪跟踪轨迹如图15所示。轨迹上各点对应关节角变化如图16所示。 从图14、图15中可以看出,虽在曲面上画圆导致各插值点的姿态信息一直在变化,但是也并未出现因各种奇异位姿而导致执行中断或是轨迹上的突变问题,整体轨迹和平面上运行时一样都呈现连续且平滑的曲线,因此可以看出运用IQPSO算法对不同轨迹上的插值点进行求解具有较为优良的稳定性和求解精度。 图16所示的关节角变化曲线和图13所示的变化曲线都一样保持了平滑连续无奇变的情况,再一次证明了利用IQPSO算法进行逆运动学求解可以达到运动控制过程中的运动平稳性原则,也与前文目标函数构建过程中的约束条件相 符合。 5 结语 本文首先根据机器人的正运动学模型,以位姿误差最小为优化目标,同时结合运动平稳性原则建立了優化目标函数,将运动学求解问题转换为优化控制问题进行分析;然后在量子粒子群算法的基础上引入Levy飞行策略改进粒子更新方式,非线性地动态调整收缩膨胀因子,采用变权重方法计算最优平均位置,从而设计了一种改进的量子粒子群(IQPSO)算法。之后模拟单点位姿和连续轨迹两种不同的求解情况进行不同算法的仿真对比实验。通过适应度收敛曲线、位姿误差变化图等仿真结果证明了IQPSO算法在进行逆解运算时具有更快的迭代速度,更高的精度和更好的稳定性。最后为了证明该算法在实际运动时的可行性,将IQPSO算法编写进控制器中进行机械臂本体的实物实验。实验结果表明,机械臂末端实际运行轨迹具有连续且平滑的特性,并没有出现明显突变或因奇异问题导致运动中断的现象,证明了该算法满足机器人实际示教运动时的稳定性 准则。 该算法基于新松自研SR4C机器人进行仿真和实物验证,理论上可以应用于其他的诸如ABB、FANUC、KUKA等品牌的6轴工业机器人模型的运动学求解,因此后续工作将根据实际情况建立不同的机器人运动学模型利用该算法进行逆解求解。 参考文献 : [1] 李冠琦, 武建德, 李瑞琴. 基于旋量理论的7自由机械臂运动学建模与分析[J]. 机械制造与自动化, 2022, 51(1):105-107. LI Guanqi, WU Jiande, LI Ruiqin. Kinematics Modeling and Analysis of Seven-degree-freedom Robotic Arm Based on SpinorTheory[J]. Machine Building & Automation, 2022, 51(1):105-107. [2] 尹宁宁, 潘松峰, 杨彦平, 等. 一类串行关节式机器人逆运动学建模与仿真研究[J]. 青岛大学学报(工程技术版), 2016, 31(4):79-83. YIN Ningning, PAN Songfeng, YANG Yanping, et al. A Kind of Serial Articulated Robot Inverse Kinematics Modeling[J]. Journal of Qingdao University(Engineering & Technology Edition), 2016, 31(4):79-83. [3] BEKEY G A. Springer Handbook of Robotics(B.Sic-iliano and O. Khatib; 2008)[Book Review][J]. IEEE Robotics & Automation Magazine, 2008, 15(3):110-110. [4] 房立金, 高瑞. 一般6R机器人逆运动学算法的改进[J]. 机械科学与技术, 2018, 37(9):1325-1330. FANG Lijin,GAO Rui. lmproving Inverse Kinematics Algorithm for General 6-DOF Robots[J]. Mechanical Science and Technology for Aerospace Engineering, 2018, 37(9):1325-1330. [5] ZAPLANA I, BASANEZ L. A Novel Closed-form Solution for the Inverse Kinematics of Redundant Manipulators through Workspace Analysis[J]. Mechanism and Machine Theory, 2018, 121:829-843. [6] KHALEEL H Z. Inverse Kinematics Solution for Redundant Robot Manipulator Using Combination of GA and NN[J]. Al-Khawarizmi Engineering Journal, 2018, 14(1):136-144. [7] LIU Yiyang, XI Jiali, BAI Hongfei, et al. A General Robot Inverse Kinematics Solution Method Based on Improved PSO Algorithm[J]. IEEE Access, 2021, 9:32341-32350. [8] SANCAKTAR I, TUNA B, ULUTAS M. Inverse Kine-matics Application on Medical Robot Using Adapted PSO Method[J]. Engineering Science and Technology, an International Journal, 2018, 21(5):1006-1010. [9] 姜濤, 曹琦. 基于改进粒子群算法的机械臂逆运动学求解[J]. 长春理工大学学报(自然科学版), 2023, 46(1):59-64. JIANG Tao, CAO Qi. Inverse Kinematics Solution of Manipulator Based on Improved Particle Swarm Optimization Algorithm[J]. Journal of Changchun University of Science and Technology(Natural Science Edition) , 2023, 46(1):59-64. [10] DU Shuxing, CUI Jiashan. An Improved Strategy of PSO for Solving Multimodal and Higher Dimensional Complicated Optimization Problems[C]∥2015 Inter-national Conference on Computational Intelligence and Communication Networks(CICN). Jabalpur:IEEE, 2015:1229-1234. [11] 孙俊. 量子行为粒子群优化算法研究[D].无锡:江南大学,2009. SUN Jun. Study on Drive System of the Full-face Rock Tunnel Boring Machine[D]. Wuxi:Jiangnan University, 2009. [12] TIAN Na, LAI C H. Parallel Quantum-behaved Particle Swarm Optimization[J]. International Journal of Machine Learning and Cybernetics, 2014, 5(2):309-318. [13] SUN J, FANG W, WU X , et al. Quantum-behaved Particle Swarm Optimization:Analysis of Individual Particle Behavior and Parameter Selection[J]. Evolutionary Computation, 2012, 20(3):349-393. [14] TURGUT O E, TURGUT M S, COBAN M T. Chaotic Quantum Behaved Particle Swarm Optimization Algorithm for Solving Nonlinear System of Equations[J]. Computers & Mathematics with Applications, 2014, 68(4):508-530. [15] ZHANG Feng. Intelligent Task Allocation Method Based on Improved QPSO in Multi-agent System[J]. Journal of Ambient Intelligence and Humanized Computing, 2020, 11(2):655-662. [16] 何光, 卢小丽, 李高西. 基于双策略协同进化的QPSO算法及其应用[J]. 计算机应用研究, 2023, 40(2):418-423. HE Guang,LU Xiaoli,LI Gaoxi. Double Strategies Coevolutionary Quantum-behaved Particle Swarm Optimization Algorithm and Its Application[J]. Application Research of Computers, 2023, 40(2):418-423. [17] LIU Yahui, CAO Buyang. A Novel Ant Colony Opti-mization Algorithm with Levy Flight[J]. IEEE Access, 2020, 8:67205-67213. [18] HAKLI H, UGUZ H. A Novel Particle Swarm Opti-mization Algorithm with Levy Flight[J]. Applied Soft Computing, 2014, 23:333-345. [19] ALKHRAISAT H, RASHAIDEH H. Dynamic Inertia Weight Particle Swarm Optimization for Solving Nonogram Puzzles[J]. International Journal of Advanced Computer Science and Applications(IJACSA), 2016, 7(10) :277-280. [20] XI Maolong, SUN Jun, XU Wenbo. An Improved Quantum-behaved Particle Swarm Optimization Algorithm with Weighted Mean Best Position[J]. Applied Mathematics and Computation, 2008, 205(2):751-759. [21] 程鑫,周書敏,匡森. 自适应混合策略的量子行为粒子群优化算法[C]∥第23届中国系统仿真技术及其应用学术年会会议论文集.合肥:合肥工业大学出版社, 2022:257-261. CHENG Xin,ZHOU Shumin,KUANG Sen.Quantum-behaved Particle Swarm Optimization Algorithm Based on Adaptive Mixed Strategy[C]∥23rd Proceedings of the China Annual Academic Conference on System Simulation Technology and Its Applications. Hefei:Hefei University of Technology Press, 2022:257-261. ( 编辑 王艳丽 ) 作者简介 : 陈卓凡 ,男,1999年生,硕士研究生。研究方向为工业机器人运动控制。E-mail:958002697@qq.com。 王斌锐 (通信作者),男,1978年生,教授、博士研究生导师。研究方向为仿生机器人智能控制。E-mail:wangbrpaper@163.com。

