基于LDA-IBES-RELM 的光伏阵列故障诊断方法

邹 凯, 曾宪文, 王 洋, 高桂革

(1. 上海电机学院 电气学院, 上海 201306; 2. 上海电机学院 电子信息学院, 上海 201306)

随着“双碳”理念的提出,新能源被加速开发和利用,其中风光装机容量占比预计到2060年将提升到60%,发电量将超过55%[1]。然而,光伏阵列是光伏发电的核心部件,其长期暴露在外,易发生一些故障,如断路、短路、遮阴、老化等[2-3]。因此,对光伏阵列进行高效准确的故障诊断研究,具有重要意义[4-5]。

现阶段对光伏阵列故障诊断的研究方法主要基于数值型数据结合机器学习模型,如支持向量机(Support Vector Machines, SVM)、反向传播(Back Propagation, BP)神经网络、RBF 神经网络、随机森林(Random Forest, RF)等[6-9],但这些算法直接用于故障诊断存在准确率不高的问题。随着大量群搜索算法的提出,学者们已经利用搜索算法优化机器学习。文献[10]利用遗传算法来优化BP神经网络,诊断精度得到了提升;文献[11]利用麻雀搜索算法对深度信念网络调参,增强了模型的泛化能力;文献[12]利用秃鹰算法优化SVM 对变压器进行故障诊断,并与布谷鸟、人工蜂群和萤火虫算法优化SVM 的模型对比,表明秃鹰算法优化后的效果最好。然而以上这些算法仍存在一些问题,算法本身可能会陷入局部最优,导致模型的最优参数难以获取,因此使用群搜索算法来优化参数,并对搜索算法进行改进。

为进一步提高光伏阵列故障诊断的准确率,本文由此展开了研究。首先利用Simulink平台建立4×3的光伏阵列模型,对正常和典型故障状态进行仿真分析,提取故障特征数据,其次利用线性判别分析(Linear Discriminant Analysis, LDA)对原始数据降维,并把降维后的数据作为故障诊断模型的输入;最后利用3个策略改进秃鹰算法来优化RELM 隐层参数,并与其他模型对比,验证本文模型故障诊断的准确性和有效性。

1 故障特征提取

1.1 故障分析

利用Matlab/Simulink建立4×3的光伏阵列仿真模型,通过对正常、开路、短路、局部阴影、轻度老化、大面积阴影、重度老化7种状态进行仿真实验,并获取大量故障数据。

将任1组串断开模拟开路,将某1光伏板正负极短接模拟短路。局部阴影将某1块板的光照强度设置在50～150W/m2,大面积阴影设置3块板的光强在50～150W/m2,轻度老化则是在某1组串联2Ω 电阻,重度老化串联8Ω 电阻,故障模拟图如图1所示。在光照强度为1kW/m2,温度为25℃的条件下生成各种状态下的P-U曲线和I-U曲线对比情况,如图2、图3所示。从图2、图3可以看出开路时的短路电流和最大功率点电流相对较小;对于短路故障,其开路电压较其他状态差别明显;阴影故障出现了多峰;老化故障的最大功率点电压和电流变化较明显,且从轻度到重度老化程度的变化,最大功率点电压和电流均在减小。因此可以选择开路电压(Uoc)、短路电流(isc)、最大功率点电压(Um)、最大功率点电流(im)和最大功率(Pm)作为部分特征量。

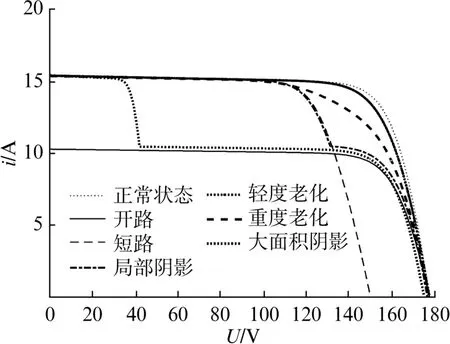
图3 各种状态下的I-U 曲线对比

在光强为400～1005 W/m2,温度在15～45℃的范围内进行仿真,总共获取1750组数据,其中训练集1400组(每种状态各200组),测试集350组(每种状态各50组)。再计算每组数据的填充因子FF,即

将以上5个参数和填充因子作为光伏故障数据的特征量。并规定正常、开路、短路、局部阴影、轻度老化、大面积阴影、重度老化的标签值分别为1、2、3、4、5、6、7。

1.2 特征降维

利用LDA 对特征量降维作为故障诊断模型的输入。LDA降维就是将原数据投影到低维的空间内,并且使同类数据尽可能聚集,异类数据尽可能远离[13-14]。利用LDA 对1.1中采集的数据降维,把降维后的数据作为最终的故障诊断特征量,至此故障特征提取工作完成,最终将此数据用于第三部分故障诊断模型的训练和测试。

2 算法原理及改进

2.1 秃鹰搜索算法(Bald Eagle Search, BES)原理

BES是由Alsattar等提出的一种启发式算法[15]。该算法模拟了秃鹰的捕食行为,分为3个阶段:选择空间,空间搜索和俯冲阶段。第1阶段为秃鹰选择空间,位置更新为

式中:Pnew,i为第i只秃鹰更新后的新位置;Pbest为最优位置;α为控制秃鹰位置变化的参数;r为随机数;Pmean为根据前一个阶段结束后得到的秃鹰平均位置;Pi为第i只秃鹰的当前位置。

α的范围在[1.5,2]之间,r的范围在[0,1]之间。

第2阶段是空间搜索,即在上一阶段搜索到的最佳空间内搜索猎物,位置更新为

式中:x(i)、y(i)为极坐标位置。

x(i)=xr(i)/max[|xr(i)|],y(i)=yr(i)/max[|yr(i)|],其范围均为[-1,1]。其中xr与yr是决定极坐标的变量,且xr(i)=r(i)sin[θ(i)],yr(i)=r(i)cos[θ(i)],θ(i)是极角,r(i)是极径,且θ(i)=απrand,r(i)=θ(i)+Rrand,α和R均是该螺旋方程控制位置的参数,范围分别在[5,10]和[0.5,2]。

第3阶段的位置更新为

式中:c1、c2为秃鹰向最优位置和中心位置的移动强度;x1、y1为极坐标位置。

c1和c2的范围均为[1,2],x1(i)=x(i),y1(i)=y(i),此时xr(i)=r(i)sinh[θ(i)],yr(i)=r(i)cosh[θ(i)],θ(i)=απrand,r(i)=θ(i)。

2.2 改进秃鹰搜索算法(Improved Bald Eagle Search, IBES)

由于种群个体收敛较快容易陷入局部最优,以及在后期因搜索空间较小也会陷入局部最优。因此针对以上问题本文对秃鹰搜索算法进行改进。

2.2.1 Logistic混沌映射 采用Logistic混沌映射对秃鹰算法初始化种群,取代传统的随机初始化种群方法,增加了随机性和多样性,使得该算法更容易搜索到全局最优解。即

式中:xn+1为混沌映射后的个体;xn为[0,1]之间的任意数;μ为分支参数,本文中取4。

改进后的初始种群为

式中:ub、lb分别为秃鹰搜索算法的上限和下限。

2.2.2 Levy飞行策略 在选择空间阶段引入Levy飞行策略,Levy飞行是一种随机游走的寻优策略,该方法凭借小步跟踪和长距离跳跃的特点帮助算法跳出局部最优。在搜索初期阶段使得秃鹰群体有着更广泛的搜索范围,在利用Logistic混沌映射初始化种群的基础上使得算法更具备全局寻优能力。更新后的秃鹰选择空间阶段的公式为

式中:δ为步长控制参数。而

2.2.3 柯西高斯变异扰动策略 在算法后期引入了柯西高斯变异扰动策略[16],加入该策略可以很好地提升后期全局搜索的能力,因此本文选用该方法对秃鹰算法进行改进。在每次迭代结束后,执行该变异操作,若更新后的位置优于当前最优位置,则替换当前全局最优解,变异扰动后的新位置为

式中:C(0,1)、G(0,1)分别为满足柯西和高斯分布的随机变量;λ1、λ2分别为1-t2/T2、t2/T2;t为每次的迭代次数;T为最大迭代次数。

2.3 算法验证

本文为验证IBES改进后的全局搜索能力,选取了文献[17]中F3、F4、F6函数测试,并规定搜索范围分别为[-10,10]、[-100,100]、[-100,100]。设置维度D=30,种群数N=30,最大迭代次数T=100,分别对粒子群算法(PSO)、灰狼算法(GWO)、BES和IBES算法进行测试,3个测试函数的收敛曲线如图4～图6所示。

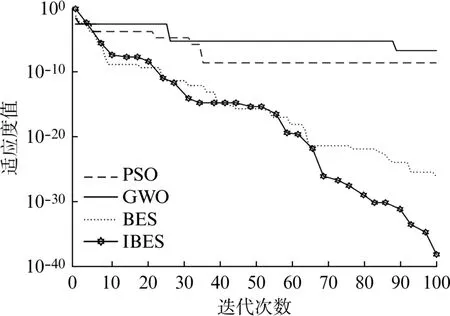
图4 函数F3测试结果对比

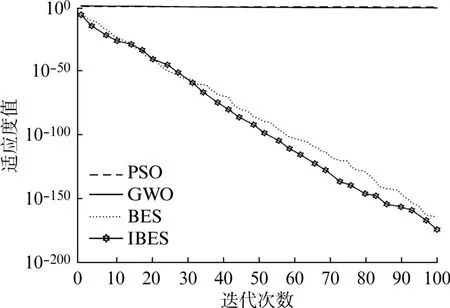
图5 函数F4测试结果对比

图6 函数F6测试结果对比

图4 ～图6均反映出在100次迭代内,IBES算法的寻优性能优于对比的3个算法。其中,PSO和GWO 算法均陷入了局部最优,只有IBES在3个测试函数下能跳出局部最优并搜索到全局最优解。从而验证了IBES算法的寻优性能较好,可有效用于对RELM 的参数寻优。

3 光伏阵列故障诊断模型

3.1 正则化极限学习机(Regularized Extreme Learning Machine, RELM)

极限学习机(Extreme Learning Machine, ELM)是单隐藏层的反馈神经网络,输入数据通过隐含层的映射,最终可以得到输出。设样本数据集(Xi,ti),其中Xi=[xi1,xi2,…,xin]T表示神经网络的输入,ti=[ti1,ti2,…,tin]T表示输出,则具有L个隐层节点的ELM 网络为

式中:wi为输入与隐含层之间的权值;bj为隐层偏置;βi为输出权重;wi·xj为wi与xj的内积;oj为网络输出;g(x)为激活函数。wi=[wj1,wj2,…,wjn]T,bj=[bj1,bj2,…,bjn]T。

为了保证输出误差最小,可以用下式表示,即

式中:H为隐含层的输出;T为预期输出。

求解β的过程就是利用最小二乘法,即β=HTT。投影后,可以得到H+=(HTH)-1HT,其中H+是H的广义逆矩阵。在计算β时,引入参数1/λ可以使该算法获得更好的泛化性能,并解决了在求解H+的过程中数值不稳定的问题[18]。利用正则化最小二乘法来求解β就是RELM 的求解过程,即

式中:λ为正则化参数。

3.2 LDA-IBES-RELM 故障诊断模型

利用1.2中降维后的数据输入到RELM 模型中,经过测试其准确率为90.29%,准确率有待提升,由于RELM 的输入层权值和隐层偏置这两个参数组合(W,B)是随机产生的,其取值对模型准确率影响较大,因此本文将2.2中的IBES算法来优化RELM 的隐层参数,搭建LDA-IBES-RELM模型。

设置模型中的适应度函数为

其中:trF、trall、teF、teall分别表示模型训练错误数、训练集总数、测试错误数、测试集总数。

该模型的实现步骤如下:

步骤1数据预处理。利用LDA 对原始数据降维,确定新的训练集和测试集及对应的标签值。

步骤2初始化RELM 的相关参数,确定IBES的相关参数,包括种群数,最大迭代次数,维度,搜索区域。利用IBES算法的混沌映射初始化种群位置(W,B),随后进行训练测试并计算适应度。

步骤3根据IBES算法更新位置,并确定每次迭代后的最优解。

步骤4判断是否已达到最大迭代次数,若是则停止搜索并输出最优参数组合(W,B),从而确定最佳的故障诊断模型。否则继续执行算法,直到满足终止条件。

3.3 仿真结果分析

本文分别对BES-RELM、IBES-RELM、LDAIBES-RELM 3 种模型做了测试对比实验,验证IBES对RELM 算法隐层参数的寻优能力以及LDA降维后的模型准确率。迭代次数设为80,种群数为30。图7反映了3种模型的适应度变化情况的对比,图8～图10分别是以上3种模型的测试结果。

图7 3种模型的适应度变化对比

由图7可知,改进后的IBES算法的寻优性能优于BES算法,且IBES算法能很快收敛到全局最优解。而与LDA降维技术结合,优化后的模型适应度最优解更佳,从0.13左右降到0.038左右,即故障诊断模型的准确率也得到提升。

根据图8分析,BES-RELM 模型的测试结果中,出现了6个正常数据诊断为故障,总体准确率为91.71%;根据图9分析,IBES-RELM 模型不存在正常数据诊断错误的情况,但依然存在大量轻度老化故障数据诊断错误的情况,总体准确率为92.86%。根据图10分析,LDA-IBES-RELM 模型就解决了轻度老化故障类别诊断准确率低的问题,该类别只有3个数据诊断错误,且开路故障的误诊数减少到4个,总体准确率达到了97.71%,比以上2种模型准确率分别提高了6%和4.85%,比传统RELM 准确率提高了7.42%。

图9 IBES-RELM 模型测试结果

图10 LDA-IBES-RELM 模型测试结果

本文还利用降维后的数据分别对PSO-RELM、GWO-RELM、BES-RELM 模型进行了测试。测试结果如表1所示。

由表1可知,秃鹰算法优化的模型故障诊断准确率优于PSO及GWO算法,且改进后的IBES算法效果更佳,同时也验证了IBES具有较强的搜索性能。

4 结 论

本文利用Simulink建立光伏阵列模型并仿真出故障数据,提出LDA-IBES-RELM 故障诊断模型,并对该模型做了训练和测试,得出以下结论:

(1) IBES 的寻优性能优于BES 及PSO 和GWO 算法,且柯西高斯变异对算法的改进效果较好。

(2) 本文提出的LDA 降维方法能够保留原始数据影响力较大的特征,并能过滤掉一些冗余特征,结合机器学习算法更能提高模型的预测准确率。

(3) LDA-IBES-RELM 模型用于光伏阵列故障诊断,训练速度快,准确率高。该模型也可以用于其他领域的故障诊断和分类问题。