城市轨道交通预约进站配额优化研究

朱亚迪, 张晓迪, 杨 晓, 孙 颖

(1.北京交通大学 土木建筑工程学院, 北京 100044;2.北京交通大学 北京市轨道交通线路安全与防灾工程技术研究中心, 北京 100044;3.北京中关村轨道交通产业发展有限公司, 北京 100044)

0 引言

城市轨道交通作为1种大运量公共交通,具有快捷经济、准时性高等特点,成为各大城市解决居民出行问题,尤其是通勤出行的主要交通方式.

城市轨道交通凭借其便捷性和准时性吸引了大量通勤乘客,导致早晚高峰时期车站内乘客严重拥挤;为此,大部分运营公司采用站外限流等方式,通过站外排队形式限制乘客进站速度,以缓解车站内乘客大量聚集. 但是,站外限流作为1种粗放型的管理手段存在较多问题:对于运营公司来说,需要配置大量人力进行引导管控;对于乘客来说,需要在站外排队等候,时间可靠性差、出行体验差. 随着互联网技术的发展,网络预约制度在各个领域广泛应用(例如医院预约挂号);通过合理的资源配置,以保证在资源紧缺的状况下协调供给与需求之间的关系,从而提升服务水平以及系统的运营效率. 在此背景下北京交通发展研究院于2020年开展了北京地铁预约出行试点工作,通过线上预约、快速进站方式减少乘客站外排队时间,提升乘客出行体验以及交通系统运营效率.

一方面,通过对居民出行时空分布的诱导干预,缓解由居民出行时空分布重叠不均引发的拥堵;另一方面,以需求为出发点提供出行供给服务,实现交通工具按需调度,提升交通出行服务质量. 而以北京为代表的大城市高峰时段通勤出行需求非常大,客流会在短时间内高度集中,造成客运资源紧张,并且新冠疫情相关政策措施更是不允许出现人员密集排队与地铁满载现象. 因此,北京在新冠疫情防控期间,选取了地铁大客流站点开展了预约进站的实践工作,依托预约出行思路,通过预约将乘客在站外的排队转变为线上排队,减少站外集聚风险.

然而,根据在北京地铁沙河站实地调研发现,在政策实行过程中,预约通道乘客到达比较分散,虽满足了乘客“即到即走”,但是存在很多通道空闲的状况,资源未能得到最大限度利用;且在利用地铁出行刷卡大数据与实际调研结果比对后发现,未实行预约政策的普通通道在出行高峰时期排队拥挤情况仅得到一定改善. 究其原因,预约试点过程中各时段的配额设定缺乏合理依据,相对偏少. 因此,为了能更好地发挥预约出行的作用,需要对预约配额进行科学合理的优化,以保证在系统能力充分发挥的前提下,尽可能减少普通通道乘客排队时间,提升乘客出行体验以及系统运营效率.

本研究旨在对城市轨道交通预约进站系统的配额进行优化研究,以实现在站点容量限度范围内最小化所有乘客的进站排队时间. 本文使用智能卡数据和实地调研数据,建立站外排队时间的优化模型,优化车站预约配额;并利用Anylogic行人仿真平台进行计算机仿真,验证地铁预约系统配额优化模型的有效性与可靠性.

1 数据获取及分析

1.1 出行特征分析

本文首先基于智能卡数据分析目标车站乘客出行高峰时段,为调研工作和模型构建提供基础;从个体角度分析通勤者每日进站时间特征,以确定预约时间粒度.

1)出行高峰时段分析

基于目前北京地铁实施预约进站的限流站点,本研究选择沙河站为研究案例车站. 利用智能卡数据,统计沙河站全天进站客流,以15 min为颗粒度进行统计,其时间分布图如图1所示. 统计结果显示沙河站早高峰较为明显且进站客流集中06:30—09:00时间段,其中峰值出现在07:00.

图1 沙河站进站客流时间分图

2)进站时间特征分析

为确定预约时间的最佳粒度,本文基于智能卡数据,对通勤乘客每日进站时间差进行统计分析,如图2所示,表明通勤乘客进站时间相对固定,如果预约时间粒度采用10 min,并提供前后10 min的缓冲时间可以保证大部分乘客进站时间需求.

1.2 车站服务能力分析

为了得到车站服务能力,本文针对车站站台容量、高峰时段站外乘客进站流率、高峰时段站外乘客排队时间、高峰时段的乘客到达率进行实地调研.

1)站台容量

本文中站台容量是城市轨道交通车站单方向站台最大承载人数. 针对早高峰时段,站台容量可以采用所有车门处最大排队人数来衡量. 多次统计高峰时段各个门口的最大排队人数,通过求和取平均值即得到车站单方向站台容量.

针对沙河站线路,其运营车辆是6节编组车辆,有24个车门. 限于调研人数限制,本文只调研每节车厢的2个车门处排队人数,得到12个车门的排队人数;将处理后的调研数据扩大两倍,即得到总体容量为R=438人.

2)普通通道服务特征

未预约乘客从普通通道进入车站,其通过能力以及新到达率决定了乘客的排队时间. 本文通过通道流率、新达到率和排队时间来衡量普通通道的服务特征.

对于通道流率,本文调研早高峰时段每2 min的通道进站乘客数量,得到高峰时段普通通道流率随时间的变化特征. 对于新达到率,本文调研相同时段内每2 min队尾新增加的排队人数,作为新到达人数. 对于排队时间,在早高峰时段每20 min从队尾选择1名排队乘客记录从进入队列到进站的总排队时间即为该时刻的排队时间.

针对本文的案例车站,通过实地调研,保留有效数据,分别绘制通道流率、新达到率和排队时间的变化趋势,如图3所示. 调研结果显示普通通道流率和新到达人数随时间呈现出较强的规律性,流率基本在60～100人/min,新到达人数在07:40后呈下降趋势;而排队时间随时间呈较明显的先上升后下降的变化趋势,表现出早高峰的产生与消退.

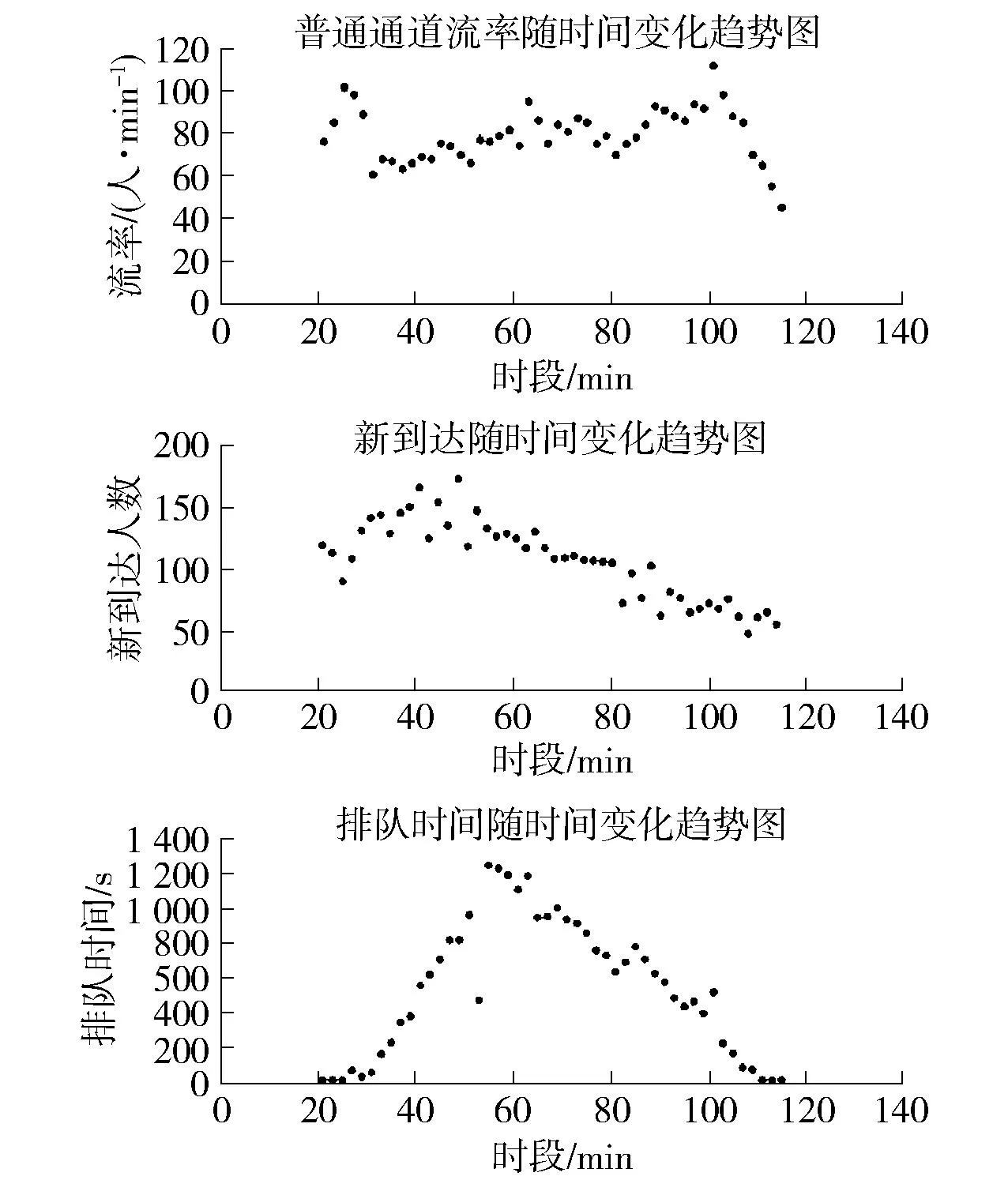
图3 各变量随时间趋势图

图4 模型概念构建图

3)现有预约配额

预约乘客可以通过预约通道直接进入车站候车,预约通道通过能力决定了预约配额. 由于目前试点站配额相对较少,很难调研得到预约通道的最大通过能力;因此,本文以普通通道的最大通过能力来表示预约通道的最大通过能力. 针对现有预约配额,本文以10 min调研时间单位,记录通过预约通道进站乘客数量;取其平均值得到目前站点预约通道的配额每100人/10 min.

2 配额优化模型构建

2.1 模型假设

1)假设预约乘客均能在预约时间段内进站;

2)假设在调研的2 min时间间隔内新到达乘客的总排队时间相同;

3)假设每次地铁进站后,站台上所有乘客均能上车,无滞留乘客.

2.2 优化模型构建

1)基于调研数据的优化模型

为了优化站点预约进站配额以达到减少乘客站外排队时间的目的,本文根据调研数据建立站外普通通道排队时间与预约进站配额等因素之间的关系,并据此构建优化模型.

表1 方案一主要参数

设t时刻时,排队人数为L(t),流率为q(t),新到达人数为a(t),时间间隔为Δt,排队时间为T.已知某时刻的排队人数等于(t-Δt)时刻的排队人数,减去t时刻的进站人数qΔt,加上t时刻的新增排队人数aΔt.

L(t)=L(t-Δt)-q(t)Δt+a(t)Δt

(1)

结合式(2),基于排队时间与排队人数和进站流率的关系,得到式(3)

(2)

(3)

基于调研数据,利用该关系式进行回归,得到排队时间的计算公式;并与式(1)结合,得到每2 min时间间隔的排队时间的递推公式,见式(4).

(4)

基于该递推关系,构造1个预约时间粒度,即10 min新到达乘客的总体排队时间.

以早高峰典型时段07:30—07:40为例,为方便表达,以07:00为基准,将07:30用30表示,07:30—07:32时段用中间时段31表示.基于式(4),得到31、33、35、37、39时段的排队时间,其中,第31和39时段的表达式见式(5).

(5)

接下来,根据每个时段的预约配额求解对应普通通道的新到达人数.此时,各时段新到达人数通过各时段调研得到的普通通道新到达人数与优化预约配额和原预约配额差值计算得到.因此,各时段的新到达人数表达式见式(6).

(6)

最终得到目标函数,见式(7).

(7)

针对以上目标函数,本文提出4个方面的约束条件:

①每个时段的排队时间应小于5个时段实际调研排队时间中的最大值.

T(i)≤max{T′(31),T′(33),T′(35),T′(37),T′(39)}
(i=31,33,35,37,39)

(8)

②所有排队时间都大于零.

T(i)≥0

(9)

③普通通道流率与预约通道流率之和应小于每分钟站台容纳量.

(10)

④目标函数应大于零.

G(X1,X2,X3,X4,X5,X6)≥0

(11)

2)基于排队论的优化模型

根据调研数据分析,地铁预约进站符合多服务台无穷输入先到先服务排队系统(M/M/n/∞/FCFS).该模型系统存在以下假设:

①乘客的到达可以被视为是无限的.

②乘客的到达是相互独立的,以前的到达对现在新到达人数没有影响.

③乘客输入过程是趋于平稳的.

④乘客的输入过程服从泊松分布,而服务时间服从负指数分布.

从而,时间t内到达n个乘客的概率为

(12)

乘客间隔服务时间T

P(T≤t)=1-e-λt

(13)

本文排队规则为等待制,即当乘客到达时,如果进站人数达到站台容量,乘客就排队等待,直到进入车站.FCFS服务即先到先服务,先到的乘客优先进入地铁站乘车.

模型构建:模型基本参数见表2:

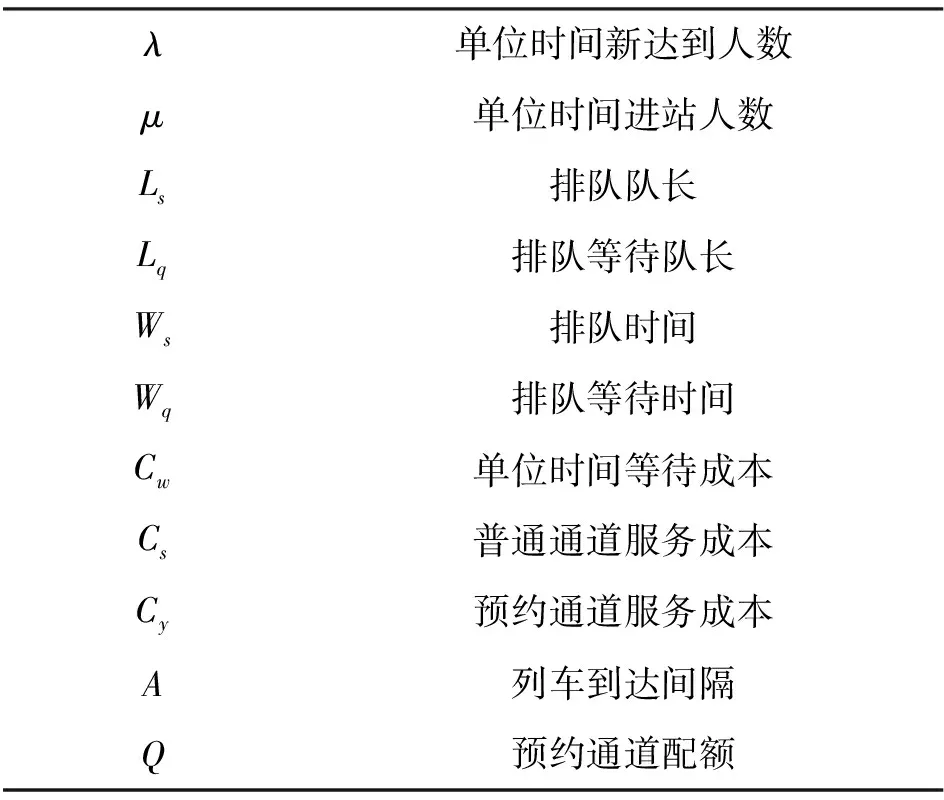
表2 基本参数介绍

1)服务过程

时间t内到达n个顾客的概率为

(14)

乘客间隔服务时间T

P(T≤t)=1-e-λt

(15)

2)服务过程

①基本排队关系

输入率=输出率

λn-1Pn-1+μn+1Pn+1=(λn+μn)Pn

(16)

系统中的平均顾客数(L)(包括等待的和正在被服务的顾客)等于顾客的平均到达率(λ)乘以1个顾客在系统中花费的平均时间

Ls=WSλ

(17)

③建立总收益函数=普通通道收益+预约通道收益-等待成本.

3)模型优化

目标函数

1)最大化总收入C

MaxC=(Cs-CqWq)(Lq-Q)+QCy

(18)

2)最小化排队时间

min(Ws)

(19)

约束条件

1)预约通道实现不排队

Q/H≤μ(max)

(20)

2)普通通道符合实际情况

μ≤μ(max)

(21)

3)排队等待时间小于列车到达间隔

Ws≤A

(22)

4)其余约束条件参考方案1

3 结果分析及仿真模拟

3.1 模型优化对比

基于MATLAB完成以上模型,并进行模型优化求解,结果见表3.

表3 各方案优化结果对比

表3中,Q为预约通道10 min内的预约配额,q为每2 min预约配额.

3.2 结果仿真验证

针对模型优化结果,本文利用Anylogic建立沙河站乘客进站仿真模型,如图5所示:将进站口分为普通通道和预约通道,设置行人从各方向到达地铁站附近,通过闸机进入地铁站. 分别对本文提出的2种模型的优化方案进行仿真,与优化之前效果进行对比.

图5 3D物理模型及仿真逻辑模型

1)仿真结果分析

统计仿真运行过程中各方案排队人数与排队时间实时数据,结果如图6所示.

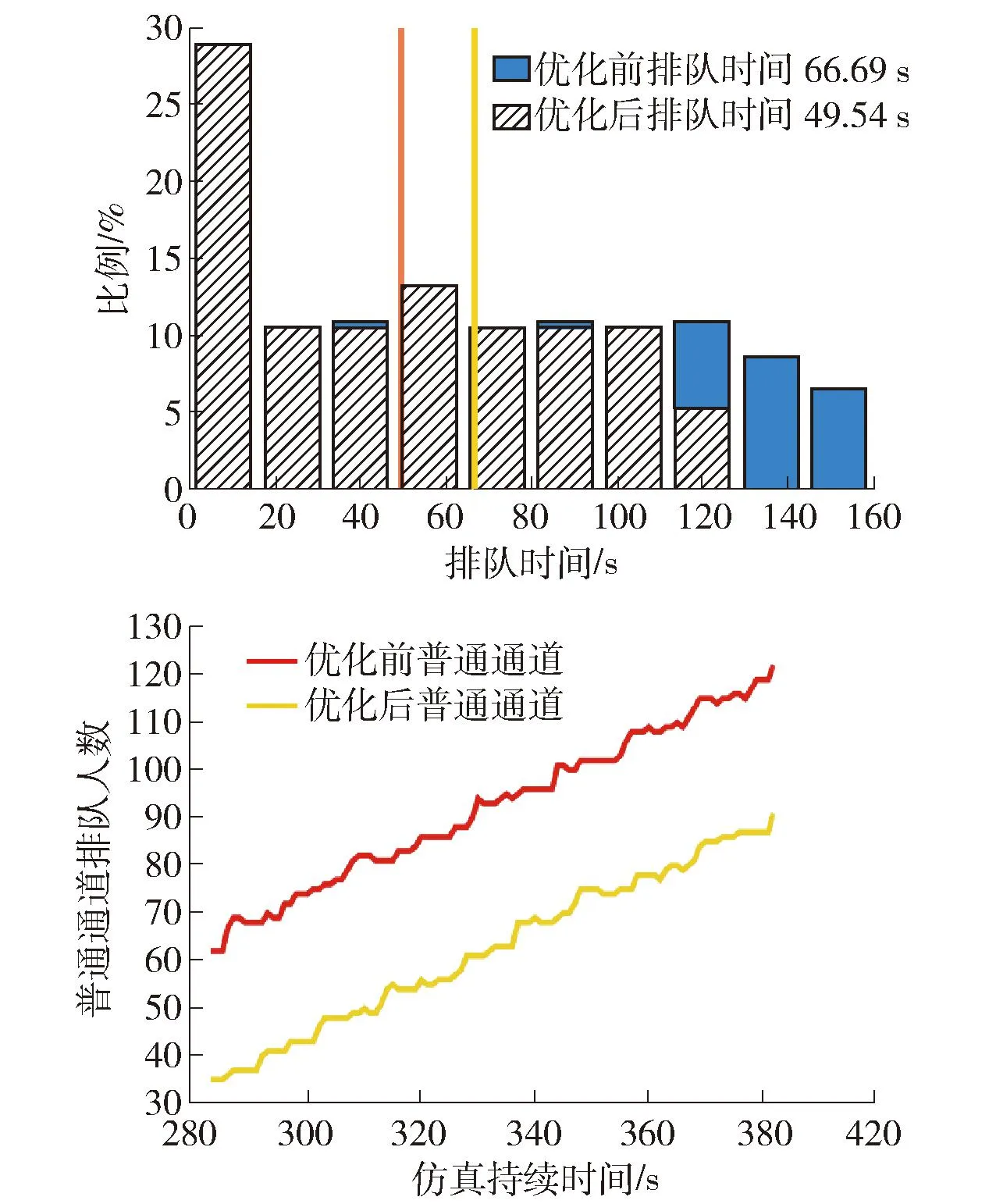
图6 方案1排队时间直方图及排队人数折线图

由图6可以看出,经方案1优化后,即预约配额增加至420,普通通道乘客进站排队时间普遍缩短,均值由66.69 s缩短至49.54 s,排队人数在也平均减少25人左右.

由图7可以看出,经方案2优化后,即预约配额310时,普通通道乘客进站排队时间均值由65.41 s缩短至52.69 s,排队人数在各阶段平均减少27人左右.

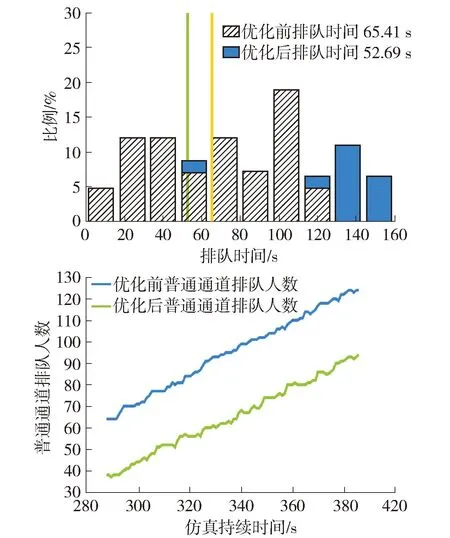
图7 方案2排队时间直方图及排队人数折线图

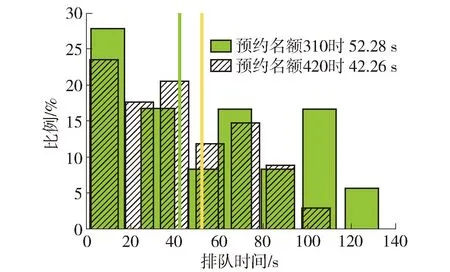
图8 方案对比排队时间

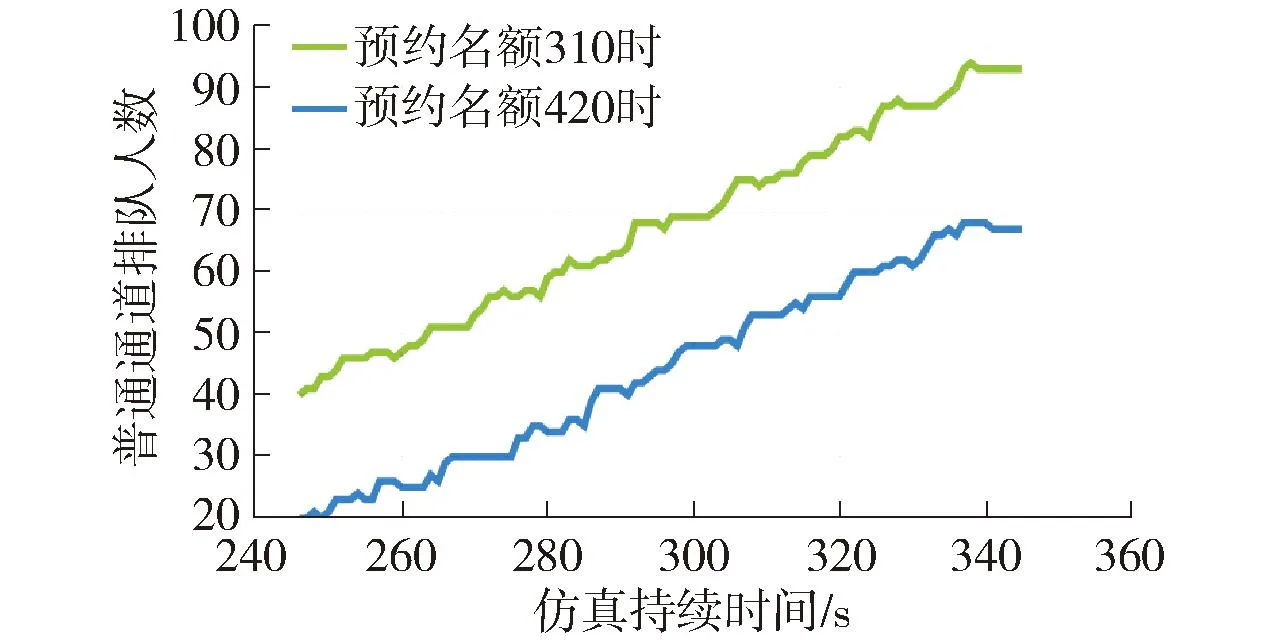
图9 方案对比排队人数

2) 仿真结果对比

针对两个方案的仿真结果,方案1比方案2缩短了总体排队时间10 s,并减少了排队人数约20人.

3.3 优化结果分析

采用方案1优化方案,本文进一步计算了08:20—08:30以及08:30—08:40的优化结果,如表4所示. 1)在08:20—08:30时间段,此时间段为地铁高峰期的时间段,优化出的结果为预约配额为359名,但相对于07:30—07:40时间段,进站客流有所减少,从而预约配额减少;

表4 优化结果

2)在08:30—08:40时间段,此时间段已经处于早高峰时段末期,新到达人数相对较少,优化出的结果为预约配额为173名,基本符合实际情况.

以上优化得到的每2 min流量均小于实际调研的最大单位流量,保证了优化结果满足现有限流政策.

通过本文建立模型并优化得知,我们提出预约配额在高峰期能够提升到300～400人;然而,目前预约方案中每10 min平均提供配额约100人,而这显然是没有充分发挥预约系统的作用的体现. 增加预约配额,可以最大程度地利用了预约系统,使乘客进站效率更高. 同时,通过优化结果也发现,在早高峰期间,不同时段的最优预约配额是不同的;因此,按照不同时段,动态调整预约配额更好地发挥系统性能也十分必要.

3.4 政策建议

基于以上分析结果,本文对城市轨道交通预约进站方案设计提出以下3点建议:

1)目前北京地铁已经实施预约进站的站点可以适当增加预约配额,进一步提高车站运营效率,减少乘客排队时间.

2)各时段的预约配额应根据客流特征动态调整,以达到资源的合理配置.

3)运营部门可利用视频监控系统,基于计算机视觉技术获取预约配额优化模型所需数据,实现预约配额的动态优化.

4 研究结论及展望

本研究基于智能卡数据分析通勤高峰时期乘客出行特征,确定预约时段;通过实地调研获取进站客流特征;利用排队论模型以及以最小化非预约乘客站外排队时间为目标的调研数据模型进行配额优化;建立了Anylogic三维模型进行仿真,得出以下结论:

1)通勤乘客进站时间相对固定,采用10 min预约时间粒度即可保证乘客进站需求.

2)普通通道流率和新到达人数呈现规律性,流率基本在60～100人/min;新到达人数在07:40后呈下降趋势;排队时间具有先上升后下降的变化趋势,表现出早高峰产生与消退.

3)针对07:30—07:40时段,调研数据模型与排队论模型对预约配额的优化结果分别为421与312;通过Anylogic仿真后发现采用调研数据模型的优化方案优于排队论优化方案及原方案,其站外排队人数与平均排队时间最少.

4)总体来看,目前提供预约名额100名,未能充分利用预约系统,应增加预约配额,必要时动态调整.

基于上述工作,后续在以下2方面展开研究:

1)在考虑预约系统“削峰”作用下进行优化预约配额的研究,由此可以实现地铁站把高峰集中出行的乘客向高峰边缘时段引导的实际需求.

2)将地铁预约出行作为新型出行模式进行研究,让其作为1种新型出行模式在超出轨道交通的领域得到更加普遍的应用.