都市圈客运走廊城际通勤方式选择演化博弈研究

费 跃, 余忠洛, 张 强

(1.东南大学成贤学院土木与交通工程学, 南京 210088; 2.中国国际工程咨询有限公司, 北京 100048)

0 引言

都市圈是“城市群内部以超大特大城市或辐射带动功能强的大城市为中心、以1 h通勤圈为基本范围的城镇化空间形态”[1]. 都市圈的发展突破了单个城市行政区划的范围,外围城市与中心城市间的城际通勤需求是其主要特点. 客运走廊是都市圈长距离快速出行的主通道,走廊内存在着轨道交通、私人小汽车等交通方式间的竞争. 既有关于出行方式选择的研究多采用离散选择模型[2-4],只能给出最终的静态结果. 有学者[5-7]将演化博弈理论应用于交通方式选择的研究中,模拟现实中交通出行者不断调整优化自己出行选择的过程. 蔡鉴明等[8-10]从出行者成本、系统收益角度出发,利用演化博弈分析了外部因素变化对出行方式结构的影响. 随着研究的深入,学者发现演化博弈中的复制动态机制在解释出行选择行为的有限理性方面存在一定的局限性[11],而基于Logit动态的演化博弈考虑了个体偏好,更符合出行者的出行决策过程. 利用基于Logit动态的演化博弈模型,Lin等[12]分析了高速公路收费政策的调整对于轨道交通和小汽车出行的影响,结果表明出行距离对免费通行政策的强化效果存在非线性影响. 牟振华等[13]研究了北京与上海间出行者的方式选择,认为高铁提速会吸引更多出行者,并将扩大其与航空的竞争范围. Zhang等[14]分析了出行者在共享汽车和私家车之间的动态选择过程,发现当共享汽车在出行货币成本上具有优势时,出行者才会选择共享汽车出行. Zhang等[15]提出了基于无差异阈值的出行方式选择演化博弈模型,计算结果表明:只有当出行方式间感知效用差异大于无差异阈值时,出行者的决策行为调整才遵循随机效用最大化原则.

既有研究对象主要集中在区域长距离运输和城市内部交通领域,而都市圈是一种高度城市化的地域空间,客运走廊城际通勤也区别于区域和城市内部出行,但目前尚缺少对于都市圈客运走廊城际通勤方式选择的演化博弈研究. 合理的通勤出行结构是都市圈城际交通健康可持续发展的重要保障,为了更加科学地分析都市圈客运走廊通勤出行方式选择行为,论文结合纯电汽车快速发展的背景,利用基于Logit动态的演化博弈模型,研究都市圈客运走廊城际通勤者方式选择的动态演化趋势,分析了轨道交通在途时间成本减少和票价降低对于城际通勤方式选择的影响,对于优化都市圈通勤出行结构,提高轨道交通运营效益以及相关政策的制定具有理论意义和实践价值.

1 模型构建

1.1 Logit动态

动态演化方程常用来描述博弈者策略选择概率随时间的变化率.假设出行起讫点之间的交通方式集合为M,共有m种不同的交通方式,xi表示出行者选择第i种交通方式的比例,ρij表示由出行方式j转换为出行方式i的条件概率.则在下1个单位时间dt内,选择出行方式i的出行者数量的变化可表示为[12]:

(1)

方程两边同时除以dt可得到期望动态演化方程:

(2)

根据二项logit模型的基本理论,令ui和uj为出行者选择方式i和方式j的期望效用函数,此时ρij可表示为:

(3)

将式(3)带入式(2)可得到两种出行方式下的动态演化方程:

(4)

1.2 出行者收益函数

都市圈客运走廊内的城际通勤者有两种出行方式可供选择:①轨道交通;②私人小汽车,表示为M={r,p},其中,r为轨道交通,p为私人小汽车.令出行者选择轨道交通的概率为x,则选择私人小汽车的概率为1-x.两种出行方式的收益函数构成主要是出行时间、费用等方面的成本.令轨道交通出行的在途时间为tr1,包括候车时间,乘坐轨道交通的时间,中途换乘时间(如有换乘);两端接驳时间为tr2,包括从家出发到达轨道交通站台的时间,以及到站下车后到达目的地的时间.使用私人小汽车出行的在途的时间记为tp1,两端接驳的时间为tp2,包括从出发地到达停车场的时间,以及从停车场达到目的地的时间.乘坐轨道交通的票价为mr1,接驳交通方式的费用为mr2.使用私人小汽车的燃料成本为mp1,其他车辆成本(包括停车、保险、清洗保养等费用)为mp2,过路过桥费为mp3.

通勤时段,当出行者较多的选择私人小汽车出行时,必然会引起高峰时段客运走廊内道路交通的拥堵,带来时间上的额外损失.而当较多出行者选择轨道交通出行时,也会带来车厢内的拥挤,造成出行体验的下降.因此在收益函数中还需要考虑轨道交通和小汽车拥挤(拥堵)所产生的额外成本,分别用cr、cp表示.同时,驾驶小汽车出行会给出行者带来一定的出行体验收益,记为rp,这也是出行者在出行成本存在差异时仍然会选择小汽车出行的原因[16].相关指标及其含义如表1所示.

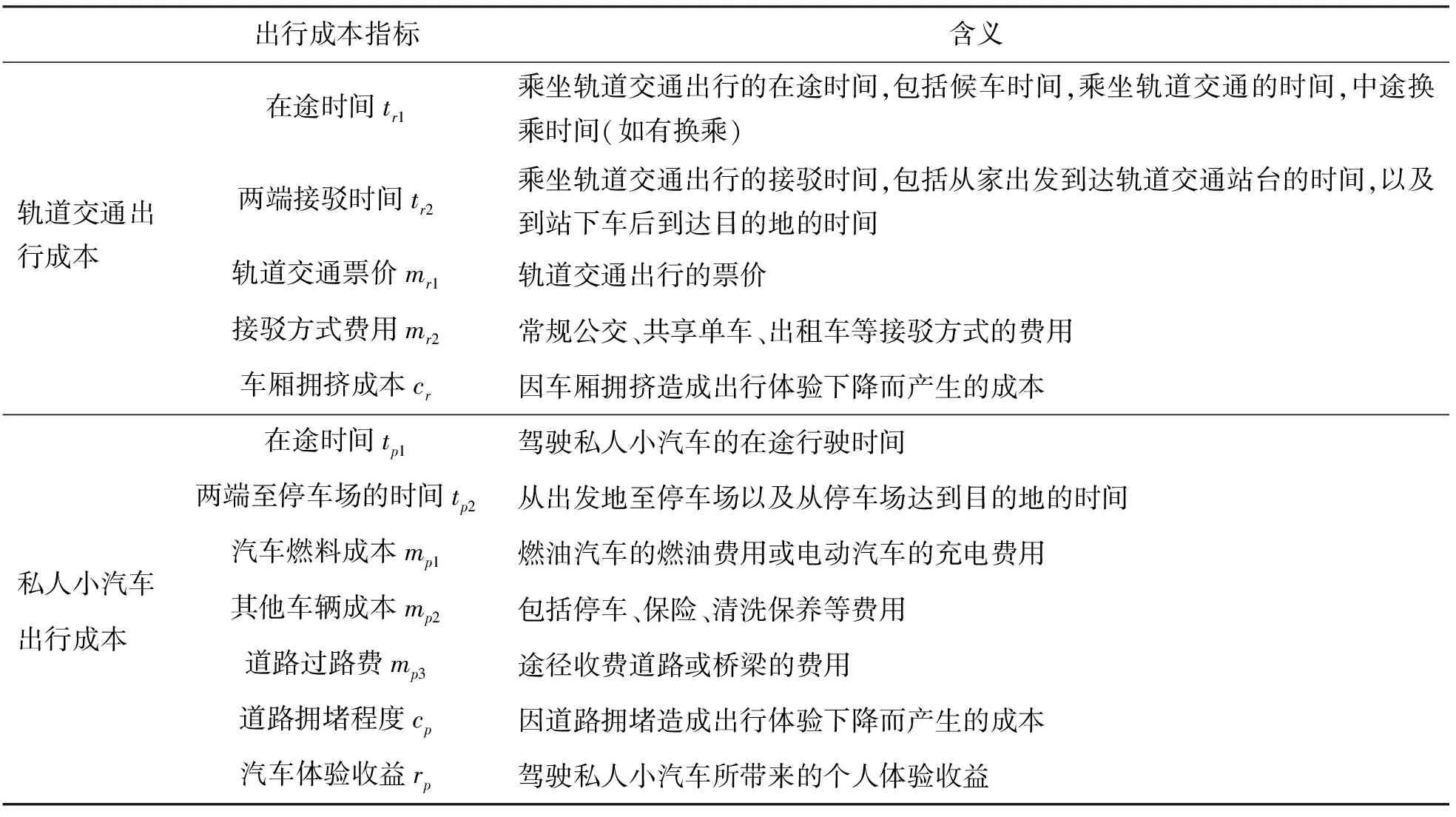
表1 出行成本指标及其含义

由上述分析可知,都市圈客运走廊轨道交通出行者的收益函数ur和小汽车出行者的收益函数up可分别表示为:

ur=-tr1-tr2-mr1-mr2-xcr

(5)

up=-tp1-tp2-mp1-mp2-mp3-(1-x)cp+rp

(6)

式中,tr1,tr2,tp1,tp2>0,cr,cp>0,rp>0,mr1,mr2,mp1,mp2,mp3>0.

1.3 演化稳定点分析

根据演化博弈的稳定性理论[17],如果是演化方程的1个均衡点,则有即:

(7)

(8)

式中,α=(tr1+tr2-tp1-tp2)+(mr1+mr2-mp1-mp2-mp3)-cp+rp,β=cr+cp.

(9)

当J<0时,处为全局稳定点,否则,动态演化博弈无法达到稳定状态.因为β>0,0<<1,所以J<0,动态演化博弈可达到演化稳定策略.同时,可通过调节轨道交通和私人小汽车的出行成本来改变α或β的大小,从而分析通勤者出行方式选择在不同条件下的演化趋势.

2 数据收集

为了保证出行者的同质性,减少地区差异的影响[14],论文利用南京都市圈宁句客运走廊内句容市居民前往南京的向心通勤活动数据进一步研究出行者在选择轨道交通或私家车时的演化趋势. 目前南京至句容间的城际交通方式主要包括轨道交通和道路交通,其中轨道交通主要依托南京地铁S6号线(宁句城际)换乘南京市区轨道交通,道路交通依托宁容快速路(S122)连接南京市区道路. 论文针对从家到工作地的单程通勤,对从句容前往南京的通勤出行者开展了问卷调查,这些出行者居住在句容,在南京工作,均具有轨道交通和私人小汽车通勤的经历.

对调查结果进行整理分析,出行者选择轨道交通的平均乘车时间为63 min,平均票价8.5元,轨道交通两端接驳的平均时间为15.1 min,两端接驳方式的平均费用为0.8元. 选择私人小汽车出行的通勤者,平均驾驶时间为71 min,两端到达停车场的平均时间为10.1 min,平均出行里程43 km. 燃油汽车的平均油耗为9.5 L/100 km,电动汽车的平均电耗为12.5度/100 km,加油的平均费用为8.0元/L,充电电费平均为0.5元/度,参与调查的出行者中,驾驶新能源汽车的比例约为21%. 小汽车出行者均选择宁容快速路出行,过路过桥费用为0,两端为家庭和单位停车位,停车费用的平均值为5元,保险、清洗保养费用平均每月为330元、90元,按每月30 d计算,则每天的费用为11元、3元. 目前,对于私人小汽车出行体验收益进行量化计算的研究较少. 有学者认为车辆价格越高,其性能和配置越好,也增加了驾驶的体验[18]. 参考Zhang等[14]的研究成果,利用车辆价格来估计出行者的驾驶体验收益,以10万元车辆为基准,假设10万元汽车产生的驾驶体验效益为10元,其他价格汽车产生的收益按照价格比进行计算. 同样,对于由车厢拥挤或道路拥堵产生的额外出行成本,因出行者个人的感知体验会存在较大的差异,论文通过问卷调查了解了出行者对于拥挤(拥堵)成本占出行总成本比例大小的感知. 调查结果显示,轨道交通出行者认为车厢拥挤成本占出行总成本比例的平均值为35%,小汽车出行者认为道路拥堵成本占出行总成本比例的平均值为15%. 根据2022年南京就业人员平均工资和工作天数计算,通勤者的时间货币价值约为63元/h. 将上述数据进行整理,将时间成本转换为货币成本,得到出行成本调查结果与货币成本取值如表2所示.

表2 轨道交通与私人小汽车出行成本均值

3 演化计算

3.1 方式选择的演化趋势

以现状调查得到的数据进行演化博弈分析,图1显示了轨道交通与私人小汽车交通方式分担比例达到均衡点时的演化轨迹. 可看出,在当前的出行成本下,不论2种方式的初始分担率是多少,系统均会演化至1个稳定的演化均衡点,约有74.0%的通勤者会选择轨道交通出行,仅有约26.0%的出行者选择私人小汽车方式. 说明在现状出行成本下,私人小汽车并不占优势,这与南京都市圈现状的通勤出行结构比例接近.

图1 现状出行成本下的演化趋势图

随着新能源汽车特别是纯电汽车的普及,车辆使用的燃料成本将有较大幅度的下降. 若通勤小汽车中纯电汽车的比例达到100%,小汽车通勤的平均燃料成本将由当前的26.5元降低到3.2元. 模型结果显示,私人小汽车的演化稳定点由26.0%提升至58.2%,即有32.2%的出行者将从轨道交通转向私人小汽车,如图2所示. 此时,轨道交通与私人小汽车相比已不具备优势.

图2 纯电汽车普及下的演化趋势图

以现状出行成本下的演化稳定策略(74.0%,26.0%)为初始点,分析不同纯电汽车比例对于轨道交通出行比例的影响. 图3显示了在小汽车出行总量中,纯电汽车出行比例每增加5%,对于小汽车出行比例增量的影响. 可看出纯电汽车比例每增加5%,小汽车出行比例增加约2.6%～3.0%,并且在最初阶段增加幅度的变化速度较快,当纯电汽车出行比例超过70%后趋于平稳.

图3 纯电汽车比例与小汽车出行比例增量的关系

3.2 成本调节对出行选择的影响

由于低廉的电力成本,使得小汽车具备了较大的竞争优势. 并且,随着都市圈交通一体化的发展,未来都市圈范围内城际高速可能会采取收费优惠的政策,这将会进一步降低小汽车的通勤时间成本. 为此,轨道交通要保证一定的客流,需要进一步降低旅客的出行成本. 由于私人小汽车的出行时间成本、燃料、保险、清洗保养的费用相对固定,而通勤出行两端的停车地点多以单位和家庭为主,收费较统一,难以配合出行结构优化进行单独的价格调整. 因此,相对可行的措施是通过降低轨道交通乘车时间和票价来提升轨道交通的出行吸引力,如开行大站快车等. 从都市圈城际快速通勤的需求角度来说,这也是最符合出行者利益的措施.

利用演化博弈进一步量化分析轨道交通在途时间成本减少和票价降低对出行方式比例的影响. 图4 显示了轨道交通在途时间成本减少时,轨道交通出行比例的变化情况. 可看出随着轨道交通在途时间成本的减少轨道交通出行比例呈现上升趋势,当在途时间成本减少超过27元(乘车时间减少约25.7 min)时,私人小汽车出行者全部转移到轨道交通. 图5显示了轨道交通在途时间成本减少的边际效应,也就是出行者对于单位成本变化的反应程度. 当轨道交通在途时间成本开始下降时,轨道交通出行比例呈现加速上升的趋势,即边际效应是逐渐增大的. 在乘车时间成本降低16元(乘车时间减少约15.2 min)时,边际效应达到最大. 此后轨道交通在途时间成本减少的边际效应呈快速下降趋势. 说明在实际运营中,一味地降低轨道交通在途时间并不经济.

图4 轨道交通在途时间成本减少与轨道交通出行比例累积变化量的关系

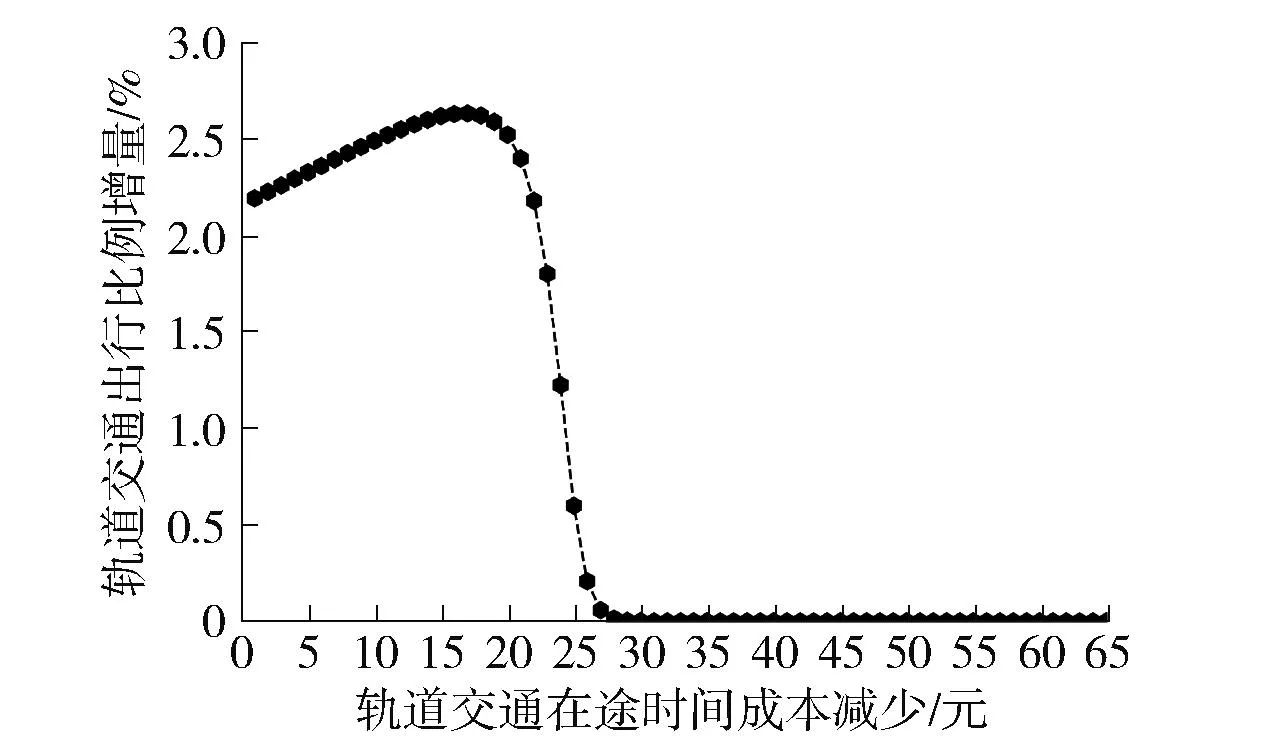
图5 轨道交通在途时间成本减少与轨道交通出行比例增量的关系

图6显示了轨道交通票价降低时,轨道交通出行比例的变化情况. 可看出随着轨道交通票价的降低轨道交通出行比例呈现上升趋势,当在途时间成本减少到0元时,也仅有约20%的私人小汽车出行者转移到轨道交通,因为此时仍存在较高的出行时间成本,相对于票价来说,时间成本对于出行者仍具有较大的影响. 图7显示了轨道交通票价减少的边际效应,可看出其边际效应是逐渐增加的,但基本在1.1%左右. 说明降低轨道交通票价对都市圈城际出行选择的影响较小.

图6 轨道交通票价降低与轨道交通出行比例累积变化量的关系

图7 轨道交通票价降低与轨道交通出行比例增量的关系

4 结束语

论文采用基于Logit动态的演化博弈模型分析了都市圈客运走廊通勤出行结构的动态演化过程,研究结果表明,由于当前较高的燃油成本,轨道交通城际通勤仍具有较大的优势,但随着纯电汽车的普及,轨道交通的竞争优势将被逐步抵消. 降低城际轨道在途时间成本(提高轨道旅行速度)或减少轨道交通票价对提高轨道交通的出行比例的影响都是非线性的,且降低在途时间成本的方式能更有效地鼓励出行者选择轨道交通. 随着都市圈的不断发展成熟,客运走廊早晚高峰将产生长距离、大客流、特定方向的集中出行[19],根据模型计算结果,对服务都市圈城际出行的轨道建议采用市郊铁路类型建设,适当扩大站间距,并在部分站点预留越站运行条件,可降低轨道交通出行在途时间成本,吸引客流,提升运营效益,并进一步优化通勤出行结构.