少开关低电压应力电流连续且共地的高增益Buck/Boost变换器

秦杨，刘宇涵，秦岭

（1.江苏大学电气信息工程学院，江苏 镇江 212016；2.南通大学电气工程学院，江苏 南通 226019）

0 引言

传统Buck/Boost双向直流变换器具有结构简单、控制方便、成本较低等优点，被广泛应用于储能系统[1，2]、可再生能源发电系统[3-5]等领域。然而，该变换器的升压能力较弱。当高、低压侧电压倍数超过5时，其占空比趋近于1，导致功率管电流应力和通态损耗急剧增大，效率明显下降[6]。此外，功率管承受较高的电压应力（等于高压侧电压），需要采用高耐压功率器件，导致通态损耗和成本较大；高压侧电流呈脉冲状，因此滤波电容承受较大的电流应力[7-9]。

为了解决上述问题，各国学者提出了多种技术方案。双电感Buck/Boost变换器实现了高压侧电流连续，减小了所需的滤波电容，但电压增益和功率管的电压应力与传统Buck/Boost变换器完全相同[10]。将中点钳位[11]或飞跨电容[12]等三电平技术引入到传统拓扑，可以使功率管的电压应力下降1/2。然而，前者的高、低压侧不共地，且负极性端的电位差呈高频PWM脉动，通过印刷电路板的分布电容产生了共模电磁干扰噪声[13，14]；后者在系统启动时需要首先对飞跨电容进行预充电，增加了结构和控制的复杂性。此外，与传统拓扑相比，三电平解决方案的开关管数量为4个，且升压能力和高压侧电流连续性没有得到改善。文献[15]提出的有源开关电感四管双向变换器能显著拓宽电压增益范围，但是其高、低压侧不共地且电流断续。此外，其还会因电感量不相等而出现振铃现象，导致功率管的实际电压应力较高（超过高压侧电压）。文献[16]提出了一种开关电容Buck/Boost变换器，该变换器的电压增益和功率管电压应力分别为传统拓扑的2倍和1/2，但同样存在不共地和高压侧电流脉动的问题。

本文提出了一种改进型Buck/Boost变换器，与传统Buck/Boost变换器相比，其增加了一个功率管，但具有更低的电压应力和更强的升/降压能力，效率较高，实现了高、低压侧共地和电流连续，降低了滤波电容的电流应力。无需采用大量电解电容并联，改善了系统可靠性。最后通过1台100 W/120 kHz的样机实验验证了该方案的可行性。

1 主电路拓扑

本文提出的改进型Buck/Boost双向变换器如图1所示。

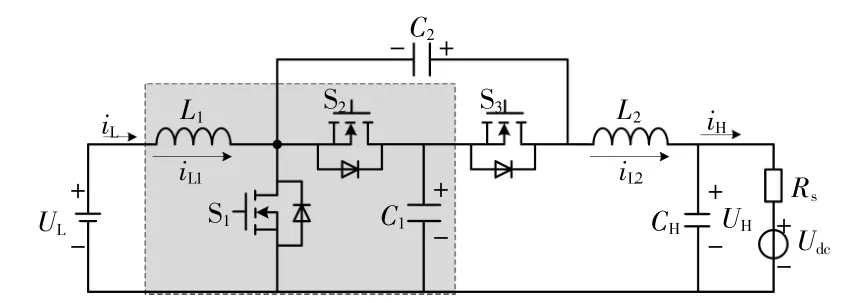
图1 所提改进型Buck/Boost双向变换器Fig.1 The proposed improved Buck/Boost bidirectional converter

图中，电感L1、开关管S1，S2和电容C1构成传统Buck/Boost电路。本文所提变换器在传统Buck/Boost电路的基础上，增加了开关管S3、电感L2以及电容C2，CH。S3与S1的驱动信号相同，与S2互补导通，本质上仍属于同步整流控制。此外，高压侧电源用恒压源Udc与内阻Rs的串联电路来等效，UL和UH分别为低压侧和高压侧的端电压。

2 工作原理

为了简化分析，用恒压源UH替代高压侧电源和滤波电容CH，并假设电容C1，C2足够大，其端电压UC1，UC2在开关周期内保持恒定。

①Boost模式

Boost模式下，所提变换器在一个开关周期内的稳态工作可以分成4个模态。其关键波形和各模态对应的等效电路如图2所示。

图2 Boost模式下，所提变换器的关键波形和各模态对应的等效电路Fig.2 Key waveforms and equivalent circuit for each mode of the proposed converter in Boost mode

模态1[t0～t1）：t0时刻，开通S1和S3。S2的体二极管DS2被强迫关断。低压侧电源UL对电感L1进行充电，电容C1经过S3对电容C2进行充电。电感L2和电容C1对负载供电。电感电流iL1和iL2分别开始上升和下降，其斜率为

t1时刻，关断S1和S3，DS2导通，模态1结束。该模态的持续时间为D1Ts，D1为S1的占空比，Ts=1/fs为开关周期，fs为开关频率。

模态2[t1～t2）：电感L1经过DS2，对电容C1进行充电，并和电容C2一起对电感L2充电。电感电流iL1和iL2分别开始下降和上升，其斜率为

t2时刻，ZVS（Zero Voltage Switching）开通S2，自然关断DS2，模态2结束。该模态持续时间为死区时间Td。

模态3[t2～t3）：L1通过S2对C1充电，并和C2一起继续对L2充电。电感电流斜率如式（2）所示。t3时刻，关断S2，DS2再次导通，模态2结束。

模态4[t3～t4）：该模态的工作情况与模态2相同。t4时刻，开通S1和S3，模态4结束，下一开关周期开始。该模态的持续时间为死区时间Td。

②Buck模式

Buck模式下，所提变换器在一个开关周期内的工作可以分成4个模态，其关键波形和各模态对应的等效电路如图3所示。

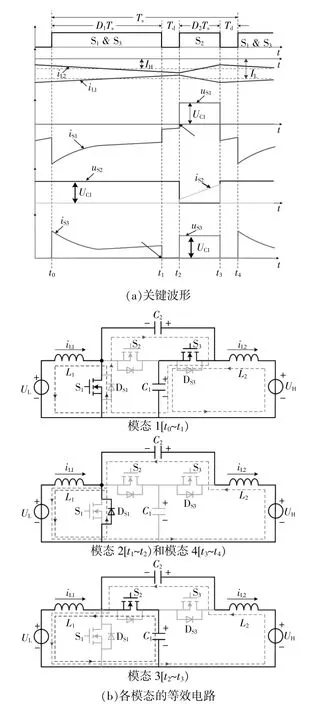
图3 Buck模式下，本文变换器的关键波形和各模态对应的等效电路Fig.3 Key waveforms and equivalent circuit for each mode of the proposed converter in Buck mode

模态1[t0～t1）：t0时刻，ZVS开通S1，S3。电感电流iL1经过S1的沟道续流，DS1自然关断。经过S3，电容C2对电容C1进行充电，高压侧电源UH对电感L2和电容C1进行充电。电感电流的变化斜率如式（1）所示。t1时刻，关断S1和S3，模态1结束。该模态持续时间为D1Ts。

模态2[t1～t2）：电感电流iL1中的一部分经过DS1续流；高压侧电源UH对电感L2、电容C2充电。电感电流的变化斜率如式（1）所示。t2时刻，开通S2，DS1被强迫关断，S1，S3端电压上升为UC1，模态2结束。该模态持续时间为死区时间Td。

模态3[t2～t3）：电容C1通过S2对电感L1进行充电，电感L2对电容C1和电感L1进行充电。电感电流的变化斜率如式（2）所示。t3时刻，关断S2，DS1导通，S1和S3的端电压重新被钳制在0，模态3结束。

模态4[t3～t4）：该模态的工作情况和模态2相同。t4时刻，ZVS开通S1，S3，模态4结束，下一周期开始。模态4的持续时间为Td。

3 稳态特性

3.1 电压增益和电压应力

根据电感L1，L2的伏秒平衡，可得：

由图3（b）可知，UC1=UC2，将该等式代入式（3），可得所提变换器的电压增益为

开关管S1，S2，S3和电容C1，C2电压应力分别为

可见，所提变换器开关管电压应力完全相同。

若以UH作为基值，则开关管的电压应力标幺值为

根据式（4）和式（6），可以绘出本文所提变换器的电压增益和电压应力特性曲线，如图4所示。可以看出，本文所提变换器最小增益为2，表明低压侧电压UL必须低于0.5UH。

3.2 平均电流应力

由于稳态时电容C1和C2的平均电流为零，故电感和开关管的平均电流为

式中：IS1，IS2，IS3分别为开关管S1，S2，S3的平均电流；IL1，IL2分别为电感L1，L2的平均电流；IL，IH分别为低压侧和高压侧的平均电流。

3.3 稳态特性比较

表1对本文和文献[4，10，12，15，16]所提双向直流变换器的稳态性能进行了对比。

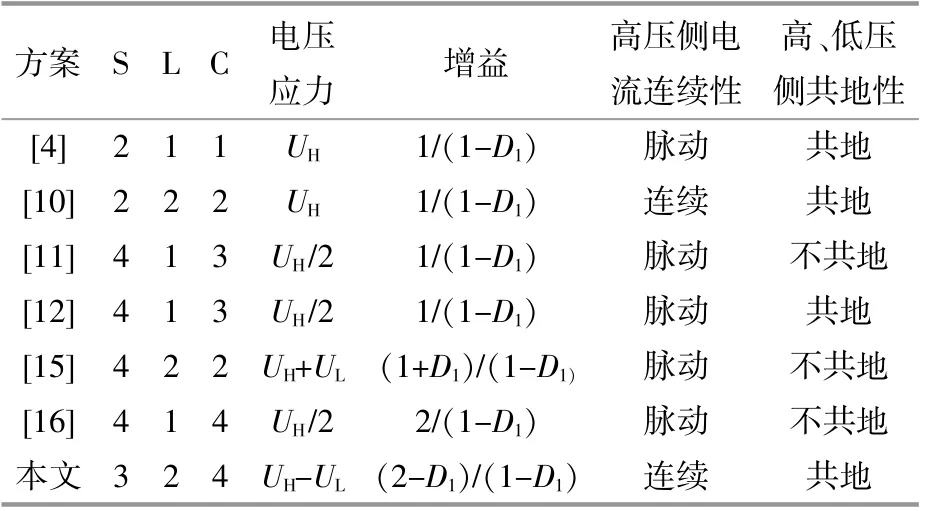
表1 不同Buck/Boost变换器方案的性能比较Table 1 Performance comparison among different Buck/Boost converter schemes

由表1可知：本文所提变换器具有较少的功率管和连续的高压侧电流，且高、低压侧共地；相同占空比条件下，电压增益与文献[15]所提有源开关电感变换器接近，高于文献[4，10，12]的拓扑，略低于文献[16]所提拓扑；电压应力远低于文献[4，10，15]所提拓扑，高于文献[11，12，16]所提方案。然而，随着低压侧电压UL增大，本文所提变换器的电压应力逐渐降低。当UL≈UH/2时，其与三电平变换器和开关电容变换器的电压应力非常接近。

4 小信号建模

为了便于分析，除了开关管S的通态电阻Ron和电感L1，L2的寄生电阻RL，忽略其他寄生参数。根据图2，3的各模态等效电路，采用状态空间平均法，可得状态平均方程为

式中：uL为输入变量；uH为输出变量；d为控制变量；电感电流iL1，iL2以及电容电压uC1，uC2和uCH为状态变量；〈·〉表示变量“·”在开关周期内的平均值，用静态工作点及其附近的小信号扰动来描述，即：

将式（9）代入式（8），并进行扰动分离和线性化处理，可得控制到高压侧电压的传递函数和控制到低压侧电感电流的传递函数：

式中：m=（2-D1）；r=mRon+2RL；z=2sRonC2；z1=2sL1；z2=2sL2；a=UC1+UC2+RonIL1-RonIL2；b=UC2-UC1-RonIL1+RonIL2；c=UC1-UC2-RonIL1+RonIL2；e=sCH+1/Rs；x=D1Ron-2Ron-2RL；k=D12-m（z+D1）；h=（D1-m）emRon；j=cm+aD1；f=xD1-mD1Ron；w=（z+2D1）m；q=emmRon-2D1+exD1；p=aD1+cm；o=（z+2D1）z；i=（m-D1-zD1）D1Ron；t=zc+c+b；u=（z+2）emRon；y1=oz1D1-of-ik；y2=oez2D1+uw-qo。

当UL=12 V，D1=0.73，C1=C2=20 μF，CH=30 μF，L1=26 μH，L2=150 μH，Ron=0.005 Ω，RL=0.01 Ω，Rs=10 Ω，输出功率Po=100 W，fs=120 kHz，Udc=48 V（Boost模式）and Udc=74 V（Buck模式）时，通过Matlab/Simulink分别绘制Gud（s）和Gid（s）的理论和仿真波特图，如图5所示。可以看出，在0.1fs以下的频段内，波特图的理论值与仿真值基本吻合。

图5 Gud（s）和Gid（s）的波特图Fig.5 Bode diagrams of Gud（s）and Gid（s）

所提变换器采用高压侧电压、低压侧电感电流的双闭环控制策略，如图6所示。

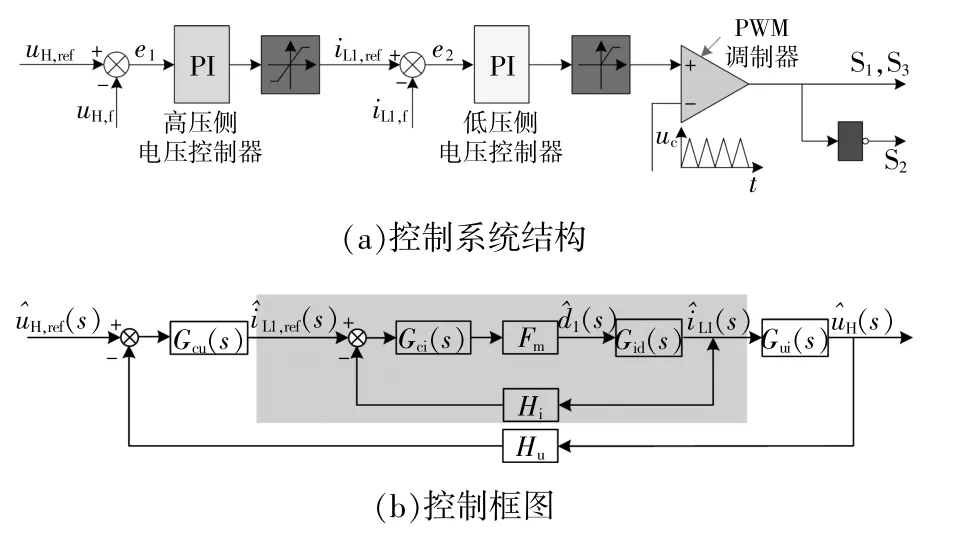
图6 所提Buck/Boost变换器的双闭环控制结构及其框图Fig.6 Double-loop control structure and block diagram of the proposed Buck/Boost converter

图中：电压外环和电流内环均采用PI控制器，传递函数分别为Gcu（s）=kp2+ki2/s和Gci（s）=kp1+ki1/s；Gui（s）为低压侧电感电流到高压侧电压的传递函数；Fm为PWM增益；Hu和Hi分别为高压侧电压和低压侧电感电流的反馈系数。

由图6（b）中的阴影部分可知，电流内环的闭环传递函数为

式中：Ti（s）=FmHiGci（s）Gid（s）为电流环的开环传递函数。

电压外环的开环传递函数为

当kp2=0.1，ki2=3 000，kp1=0.1，ki1=200，Fm=1/2.4，Hi=0.1，Hu=0.05时，Boost和Buck两种模式下，开环传递函数Ti（s）和Tu（s）的波特图如图7所示。

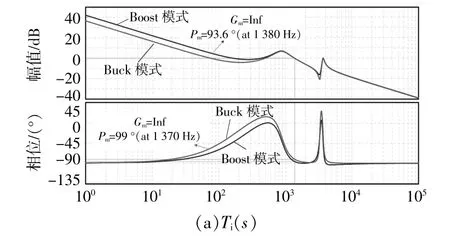
图7 开环传递函数的波特图Fig.7 Bode diagrams of open loop transfer functions

由图7可以看出：两种模式下，Ti（s）的增益裕度Gm无穷大，相位裕度Pm均大于90°；Tu（s）的增益裕度Gm和相位裕度Pm远大于0，且交越频率约超过1 kHz。这表明当前控制器参数可以确保所提双向变换器稳定运行，且具有足够的鲁棒性和较好的动态特性。

5 仿真和实验验证

为了验证所提Buck/Boost变换器的可行性，本文设计并制作了一台实验样机，如图8所示。其设计指标：Po=100 W，fs=120 kHz，UL=12 V，UH=56 V。主电路参数如表2所示。

表2 实验样机主电路参数Tabel 2 Main circuit parameters for the prototype

图8 所提双向变换器实验样机Fig.8 Experimental prototype of the proposed bidirectional converter

本文所提变换器采用的是同步整流控制，为了避免直通现象，需要设置死区。死区时间Td过长，会导致开关管的体二极管导通时间相应增大，通态损耗增大；但Td过短，会增大输出电容引起的开关损耗，导致轻载效率下降[17]。权衡考虑，设置Td=100 ns。控制电路以PWM控制芯片SG3525为主控核心。电压外环和电流内环控制器均采用PI调节器，参数分别为kp1=0.1，ki1=3 000和kp2=0.1，ki2=200；高压侧电压和低压侧电感电流分别采用分压电阻和LEM电流传感器LA25-NP进行测量，采样系数分别为H1=0.05和H2=0.1。

图9，10分别为UL=12 V，UH=56 V且满载时，所提变换器在Boost模式和Buck模式下的稳态实验波形。

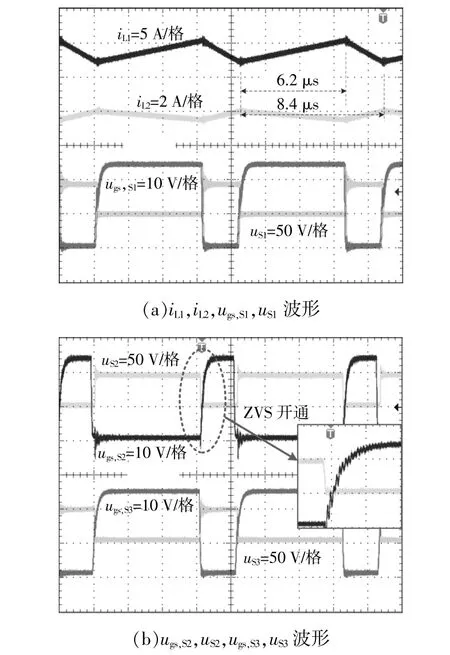
图9 Boost模式下，UL=12 V，UH=56 V且Po=100 W时的稳态实验波形Fig.9 Steady-state experimental waveforms in Boost mode when UL=12 V,UH=56 V and Po=100 W

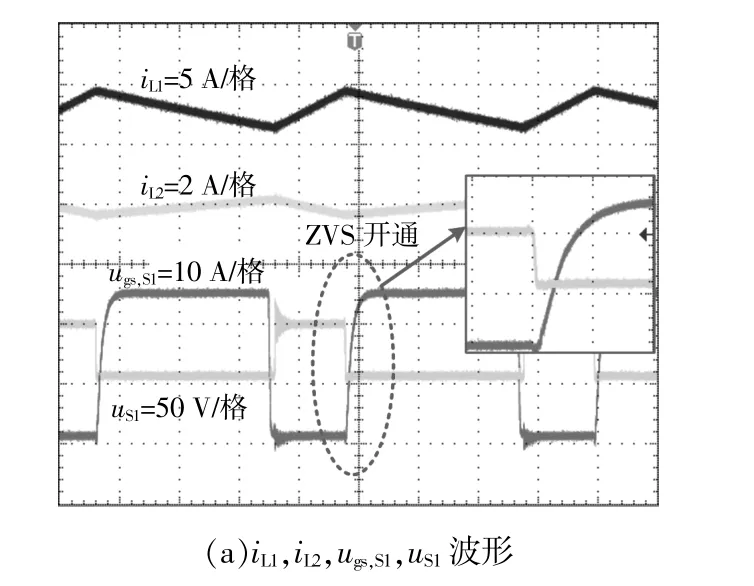
图10 Buck模式下，UL=12 V，UH=56 V且Po=100 W时的稳态实验波形Fig.10 Steady-state experimental waveforms in Buck mode when UL=12 V,UH=56 V and Po=100 W

由图9，10可以看出：电感电流iL1和iL2均连续，但变化规律相反。开关管S1～S3的实测电压应力约为44 V，与理论值基本吻合。Boost模式下，开关管S2的驱动信号ugs，S2的上升沿到来前，其端电压uS2已经下降到0，表明S2实现了ZVS开通。Buck模式下，开关管S1，S3的驱动信号ugs，S1，ugs，S3的上升沿到来前，其端电压uS1，uS3已经下降到0，表明S1，S3实现了ZVS开通。占空比D1≈0.73，理论增益为4.7；与实测增益Gboost=56/12=4.67基本吻合，从而验证了理论分析的正确性。

图11为Boost模式下，UH=56 V，低压侧电压UL和负载功率Po分别变化时所提变换器的瞬态实验波形。

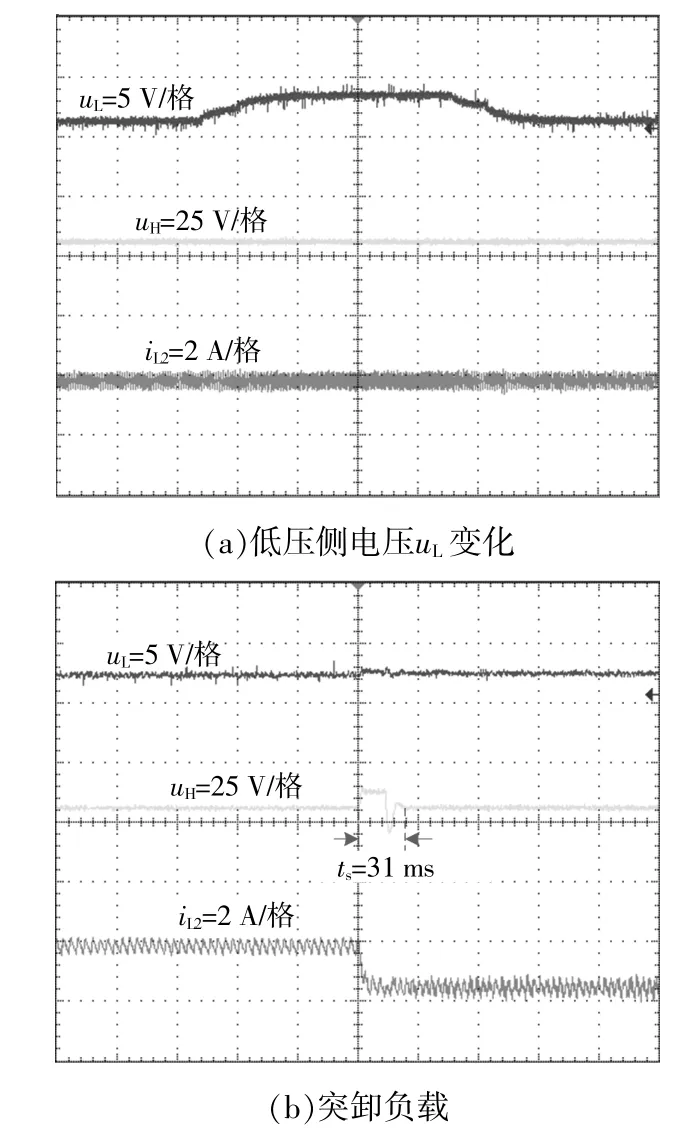
图11 Boost模式下的瞬态实验波形Fig.11 Transient experimental waveforms in Boost mode

由图11可以看出：UL在12～14 V变化，但高压侧电压UH始终稳定在56 V；当负载功率由100 W突卸至20 W时，经过约31 ms的调节过程，系统重新进入稳态，高压侧电压仍稳定控制在56 V。

图12为满载条件下所提变换器的Buck/Boost模式切换实验波形。该实验中，低压侧采用标称电压12 V的松下铅酸电池，高压侧采用直流电压源串联电阻来模拟48 V蓄电池。

图12 UL=12 V，UH=56 V且满载时的实验波形Fig.12 Experimental waveform under full-load condition when UL=12 V,UH=56 V

由图12可以看出，模式切换前后，电感电流iL1的方向发生变化，且高压侧电压能始终稳定在56 V，基本没有超调。表明所提控制策略可以实现高压侧的恒压控制和工作模式的快速平滑切换。

实验中，采用数字功率分析仪测量UL=12 V，UH=56 V时，两种工作模式下所提变换器和传统Buck/Boost变换器的效率，如图13所示。

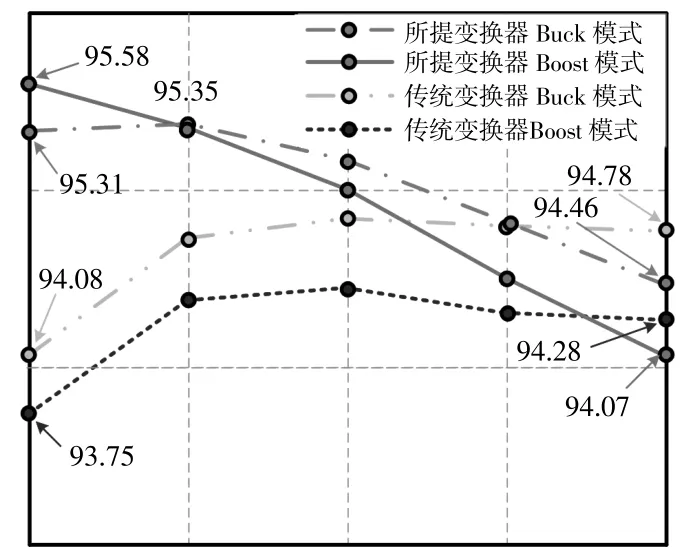
图13 实测效率曲线Fig.13 Measured efficiency curve

由图13可以看出，和传统Buck/Boost变换器相比，本文所提变换器的满载效率非常接近，约为94.5%（Buck模式）和94.1%（Boost模式），但是轻载效率明显提升，约为95.3%（Buck模式）和95.6%（Boost模式）。

图14给出了高压侧蓄电池内阻R=0.25 Ω，满载且相同输出滤波电容量的条件下，所提变换器和传统Buck/Boost变换器的高压侧蓄电池电流io的快速傅里叶变换（Fast Fourier Transform，FFT）仿真结果。

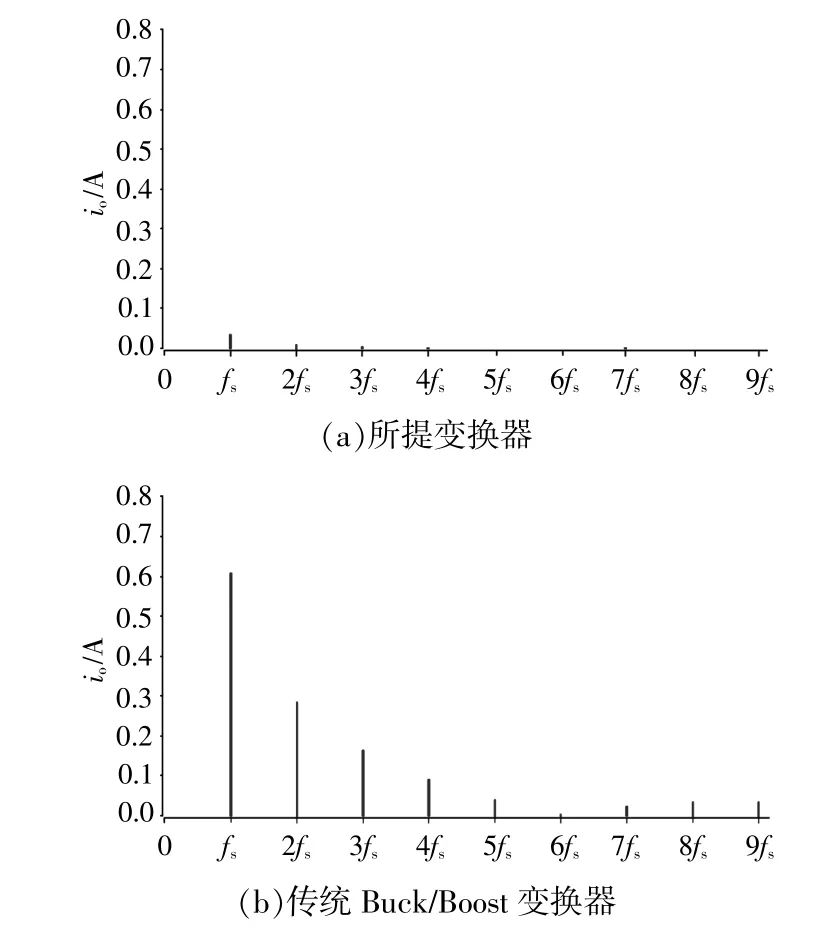
图14 高压侧蓄电池电流的FFT仿真结果Fig.14 FFT simulation results of high-voltage side battery current

由图14可知，高压侧蓄电池电流的谐波主要分布在开关频率及其倍频处，且随着谐波次数的增加，谐波幅值逐渐下降。与传统Buck/Boost变换器相比，所提变换器显著降低了高压侧蓄电池的电流谐波，具有明显的优势。

6 结论

本文提出了一种改进型Buck/Boost变换器，并通过100 W/120 kHz样机实验验证了其可行性。研究结果表明，所提Buck/Boost变换器具有较少的开关管数量，可实现能量双向流动和工作模式的平滑切换，且输入、输出共地，结构和控制相对简单。与传统Buck/Boost变换器相比，其电压增益比增大了1倍，电压应力下降为高、低压侧电压之差，因此降低了开关损耗和通态损耗，变换效率更高；更重要的是，所提变换器具有连续的高压侧电流，可避免采用大容量电解电容，特别适用于高压侧为低内阻电源或对可靠性要求较高的场合（如电动汽车等）。但需要注意的是，该变换器的最小增益为2，因此低压侧电压不能超过高压侧电压的1/2。