考虑可再生能源出力不确定性与碳排放成本的台区运行优化策略研究

王建波，秋泽楷，张小庆，豆敏娜，刘啸，卢俞帆，吕锡林，王俪蓉

（1.国网陕西省电力有限公司电力科学研究院，陕西 西安 710100；2.华北电力大学，北京 102206）

0 引言

随着金融行业的发展和电网公司的市场化改革，各类社会资本将逐步涌入电力市场，配电网下辖的台区和配电网本身都将隶属于不同的利益主体，各利益主体为了追求最大的自身利益相互竞争，形成多主体博弈格局。本文建立了由配电网运营商和其下辖的台区构成的一主多从博弈模型，实现各主体之间的利益均衡。首先运营商制定动态电价，然后各台区对电价做出响应，合理制定内部分布式电源出力以及与运营商的能量交易。

在“双碳”背景下，我国能源结构清洁化转型步伐日益加快，大量分布式能源（Distributed Energy Resources，DER）接入配电网台区（Transformer District，TD），提升了配电网能源构成清洁性的同时，源侧不确定性也使配电网调度运行风险进一步提升。目前，为降低不确定性影响，实现分布式可再生能源有效分层调控，将同一配电TD下的分布式可再生能源机组、分布式火电机组、储能以及部分可平移负荷作为整体进行统一调控[1]，在TD内部优先平抑可再生能源出力的不确定性[2]。

相关研究基于马尔科夫[3]、Coulpa[4]和ARMA[5]等方法生成可再生能源预测出力曲线[6]，本文采用蒙特卡罗法生成风光出力的预测曲线。由于可再生能源出力具有不确定性，预测出力曲线与实际出力曲线存在误差，导致出现弃风弃光的风险。目前，已有较多研究将条件风险价值（Conditional Value at Risk，CVaR）理论用于量化可再生能源不确定性所造成的运行风险。文献[7]运用CVaR理论度量风电不确定性引发的调度风险，建立了基于CVaR含碳捕集电厂与风电的电力系统的综合低碳优化调度模型。文献[8]运用CVaR理论量化虚拟电厂内分布式光伏发电的不确定性，构建了计及光伏出力不确定性的一主多从日前优化调度模型。文献[9]运用CVaR理论度量综合能源系统中源荷两侧的不确定性，建立考虑电源侧的风、光出力和负荷侧不确定性的综合能源经济调度模型。文献[10]利用鲁棒优化论（Robust Optimization，RO）和CVaR理论描述风光出力不确定性风险，构建虚拟电厂规避运行风险优化模型。本文基于上述研究，运用CVaR理论量化TD内弃风、弃光风险。

目前，为控制全球“温室效应”进一步加剧，已有多国建立了碳排放权交易市场，截至2022年1月，全球共有25个碳市场正在运行，还有22个碳市场正在建设或准备建设中[11]。为实现“双碳”目标，我国构建了碳排放权交易体系，引入了碳排放配额。碳配额的分配方式主要分为有偿、无偿分配两种，为刺激碳市场交易，通常采用基于基准线的无偿分配方式为各参与主体分配碳配额。文献[12]将碳交易成本作为风光火储系统优化目标之一，构建了碳交易与碳捕捉成本达到均衡的碳排放调度模型。

配电网中高比例可再生能源的接入虽造成了不确定性风险，却能够有效降低碳排放，进一步实现能源清洁化转型。因此，亟需在可再生能源出力的不确定性风险与清洁性收益间找到平衡，在规避不确定风险的同时降低TD内的碳排放量。本文将各TD主体在碳市场交易中的收益加入配电网运营商（Distribution System Operator，DSO）收益的目标函数，以量化发电的清洁成本，并在各TD的运行成本中加入不确定性导致的弃风、弃光风险成本。

综上所述，本文在现有研究的基础上，同时考虑了配电TD内的分布式可再生能源出力不确定性引起的调度风险和各TD主体的发电碳排放行为。首先，为协调DSO和其下辖TD之间的利益关系，建立了由DSO和其下辖的多个TD所构成的主从博弈模型；然后，通过引入CVaR理论量化可再生能源出力不确定性造成的运行风险；最后，通过BP神经网络拟合将双层主从博弈模型简化为单层模型，并运用粒子群算法进行求解。

1 多台区能量管理的主从博弈模型

为平抑分布式可再生能源出力的不确定性，将隶属于同一配电TD的分布式光伏（PV）、风电（WT）、微型燃气轮机（MT）、电能存储装置（ES）以及可中断负载（Interruptible Load，IL）作为整体，以安全性和经济性为目标，由DSO统一调控参与电力市场和碳市场交易。基于此，本文提出了一种DSO及其下辖TD的电量交易模式，如图1所示。在每个时段内，TD与DSO的购售电价是由DSO实时制定的，然而该时段内的TD内部发电量和耗电量可能不平衡，若某TD对外呈现电量富余称之为“富电TD”，若某TD对外呈现电量缺乏称之为“缺电TD”，若某TD内部能够实现供需平衡称之为“平衡TD”。“富电TD”将多余电量按照售电价格卖给DSO，“缺电TD”则按照购电价格向DSO购买所需电量。DSO根据各TD电量的供求状况，通过购售电价与主网进行电能交易，实现配电网的能量供需平衡，并在该过程通过电价差价赚取收益。

图1 DSO与TD的电量交易关系Fig.1 Relationship of exchange energy between DSO and TD

除此之外，DSO带领所辖TD参与碳市场交易，火电机组发电量参与碳配额交易[11]；可再生能源发电商在碳交易市场中通过出售国家核证自愿减排量（Chinese Certified Emission Reduction，CCER）获利[13]。DSO通过协调所辖TD的分布式火电与可再生能源发电设备出力使其自身在电碳市场的综合收益最大。

由于DSO和TD属于不同的利益主体，可将二者的主体分别视为博弈的领导者和跟随者，如图2所示。在此交易模式结构中，作为领导者的DSO能够制定与各TD的电量交易价格，制定电价之前DSO须要收集其下辖所有TD提交的购售电量数据，结合电力市场的购售电价、碳市场的碳价及碳配额总量，合理制定其与TD间的交易电价，以实现自身收益最大化。各TD则作为跟随者，根据DSO设定的交易电价，进一步考虑风光出力的不确定性所带来的运行风险和清洁能源补贴所带来的收益，以降低自身综合运营成本为目标，调整自身内部的DER和负荷的发用电量。

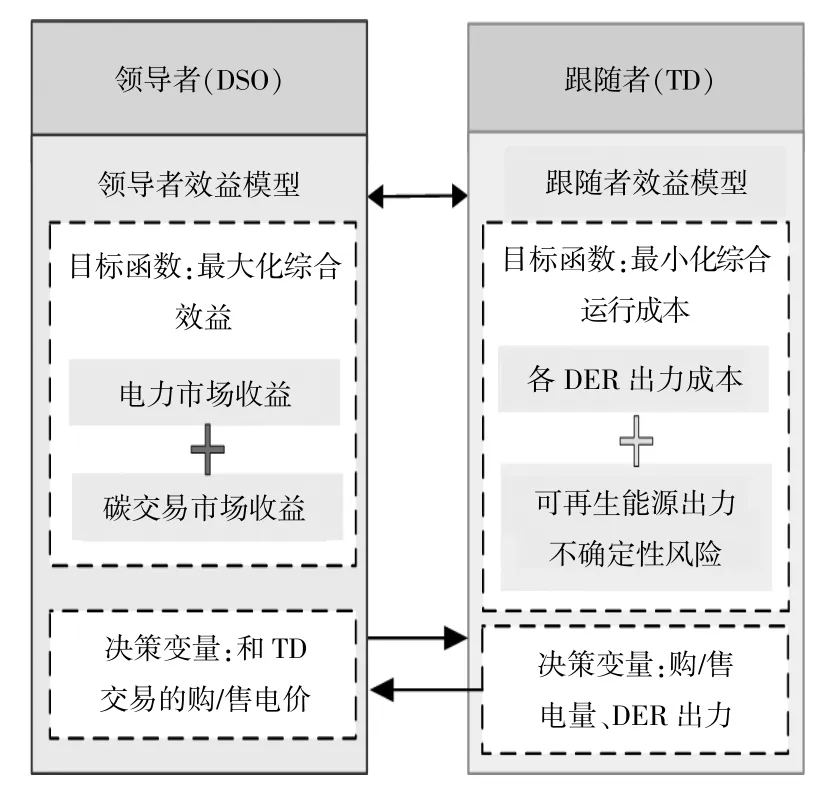
图2 主从博弈框图Fig.2 Framework of stackelberg game mode

1.1 领导者效用模型

1.1.1 效用函数

DSO作为主从博弈的领导者，以最大化自身收益为效用函数，如式（1）所示。此处收益包括DSO参与电力市场能量交易的收益、DSO参与碳交易市场的收益和DSO与各TD交易的收益。

CCAR的计算方法如式（4）～（6）所示。

式中：CFP为分布式火电机组参与碳配额交易的收益；CRP为可再生能源发电商出售CCER的收益；λC为碳价；γref为单位电量的碳排放配额；γj，i为第j个TD内的第i个MT的碳排放系数；为t时刻第j个TD内的第i个MT发出的有功功率；λCCER为碳市场内单位CCER的交易价格；分别为第j个TD内的第m个WT和第n个PV的发电量与CCER的转换系数[13]；分别为第j个TD内的第m个WT和第n个PV发出的有功功率。

1.1.2 约束条件

DSO在制定与TD交易的购售电价时，应满足如下约束：

满足上述约束可确保各TD在最小化综合运行成本时优先选择与DSO交易，而非直接向主网购售电。由式（7）可以确定DSO制定的策略空间ΩDSO，如式（8）所示。

1.2 跟随者效用模型

TD根据DSO制定的购售电价和碳配额做出响应，确定其内部的各DER出力以及与DSO的交易电量，追求自身利益最大化，如图3所示。

图3 TD响应机制Fig.3 Respond mechanism of TD

1.2.1 效用函数

在主从博弈中，作为跟随者的TD以最小化全时段内自身运行成本为目标函数，如式（9）所示。

式中：ai，bi，ci为t时段第j个TD中第i个MT的发电成本系数；第j个TD中第k个ES的调度成本系数；第j个TD中第m个WT发电成本系数；为第j个TD中第n个PV的发电成本系数；为第j个TD中第r个IL的中断补偿电价。

1.2.2 台区弃风、弃光成本

CVaR是基于风险价值（Value at Risk，VaR）演变而来的一种风险分析方法[14]，与常规的风险度量方法如VaR、敏感度分析法（Sensitive Analysis，SA）[15]相比，CVaR在预测“尾部风险”[16，17]、保持正齐次性和传递不变性方面表现出明显的优势。本文运用CVaR理论研究TD内由风光出力不确定性所引起的弃风、弃光风险成本。

首先，通过风光出力偏差来衡量不确定性造成的运行损失，构造损失函数如下：

出力偏差过大会导致弃风、弃光量增加，设上述出力偏差不超过一定阈值α的概率为函数如式（17），（18）所示。

在给定的置信水平β下，根据VaR理论的定义，构造风光出力偏差的VaR值，如式（19），（20）所示。

在VaR的基础上，进一步计算风光出力偏差的CVaR值，如式（21），（22）所示。

式中：σm，σn分别为第m个WT机组和第n个PV的弃风、弃光成本系数。

1.2.3 约束条件

在响应DSO设定的电量交易价格的同时，TD必须确保内部功率平衡，各DER也要满足各自的运行约束。

式中：式（29）为t时段内第j个TD的功率平衡约束；式（30），（31）分别为TD与DSO的能量交易约束；为第j个TD与DSO的交易电量；θj，t为布尔变量，用于描述TD的购售电行为，θj，t=1时表示在t时段第j个TD向DSO售电，θj，t=0表示TD向DSO购电；为第j个TD与DSO交易的最大电量；式（32）为MT运行约束；为t时段第j个TD中的第i个MT的最大输出功率；，分别为MT向下、向上的爬坡率；式（33）为t时段第j个TD中的第k个ES的运行约束；为t时段ES的荷电状态；分别为荷电状态的上、下限值；分别为ES充放电功率的上、下限值；Ek，max为ES最大能量容量值；式（34）为IL的中断电量约束；为t时段第j个TD中的第r个IL的最大中断量；式（35）为WT的运行约束；为t时段第j个TD中的第m个WT的最大输出功率；式（36）为PV的运行约束；为t时段第j个TD中的第n个PV的最大输出功率。

1.3 主从博弈模型

由DSO和TD构成的主从博弈模型可记为

若在对方现有策略的影响下，领导者与跟随者双方都无法通过改变策略来提升自己的收益时，主从博弈到达平衡点。

式（38）也可记为双层形式：

2 主从博弈模型求解

主从博弈模型通常有两类求解方法：一类是传统的数学方法，即通过KKT条件将双层模型转换成单层模型，但在本文的主从博弈模型中，由于式（31）中含有布尔变量θj，t，导致该方法不适用；另一类方法是直接采用启发式算法求解双层模型[18]，这类方法求解过程往往过于复杂，求解时间较长。

BP神经网络（Back-Propagation Neural Network，BPNN）能学习和存贮大量的输入-输出模式映射关系，无需事前揭示描述这种映射关系的数学方程。BPNN在处理函数逼近问题时，直接利用样本数据来实现输入和输出的非线性映射，在样本数据中自动逼近最佳刻画样本数据规律性的函数。因此，本文提出了一种BPNN结合粒子群算法的主从博弈均衡解求解算法，采用BPNN拟合并取代TD内部的能量管理模型，有效地避免了上述两种方法的弊端。

2.1 用BPNN建立拟合模型

本文所构建的BPNN输入层的物理量为T个时段的售电价λTD，s和购电价λTD，b，输出层的物理量为T个时段的各TD与DSO的交易电量，隐含层的层数为单层，最终得到输入输出参数的映射关系，如式（40）所示。

式（39）的主从博弈模型可转换为单层模型，如式（41）所示，其中购售电价λTD，b，λTD，s为模型决策变量。

2.2 主从博弈均衡解求解算法

本文采用了基于BPNN的主从博弈均衡解求解算法，其步骤如下。

步骤1：初始化系统参数。对参数进行初步设定，包括DSO通过电力市场与主网进行能量交易的上网电价和电网电价、TD内部各DER的参数、主从博弈均衡解求解算法中BPNN和粒子群算法的参数等。

步骤2：场景生成。采用MCS法，基于风光出力的历史数据，生成包含概率信息的风光出力预测值；采用拉丁超立方采样（Latin Hypercube Sampling，LHS）法，基于现有电价数据，生成K个起始样本点，记为中每个样本点的两个数值代表一组购售电价，如式（42）所示。

步骤6：将现有的样本数据集Bj带入式（1）中，得到每一组对应的上层目标函数值，即DSO在k场景下的收益。依据计算结果，将DSO的策略空间ΩDSO划分为Nl个重要区间，每个关键区间的上层目标函数即DSO收益最优值记为。

步骤10：对各个区域的最优解进行比较，可得出当前循环的全局最优解，如式（45）所示。

步骤12：判断是否达到迭代收敛标准，若达到迭代收敛标准，则停止迭代并输出均衡解，否则返回步骤4。

3 算例分析

3.1 算例说明

本文构建了一个含有3个TD的仿真系统，每一个TD包含WT，PV，ES及MT等不同种类的DER，TD中的微型燃气轮机参数如表1所示，储能参数如表2所示，风光出力预测曲线如图4所示，负荷曲线如图5所示。

表1 微型燃气轮机参数Table 1 Parameters for MT

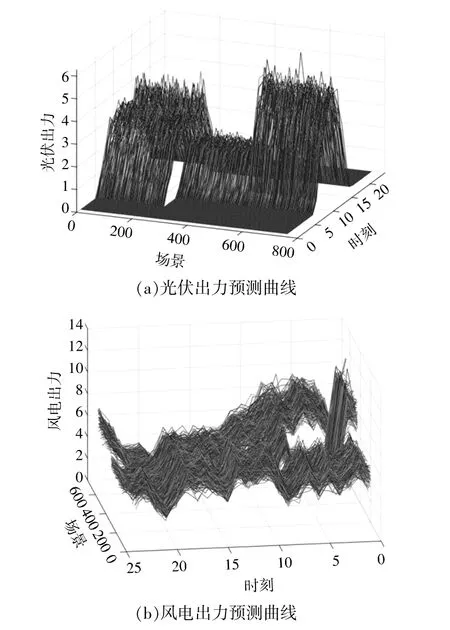
图4 风光出力预测曲线Fig.4 Prediction power of PV and WT

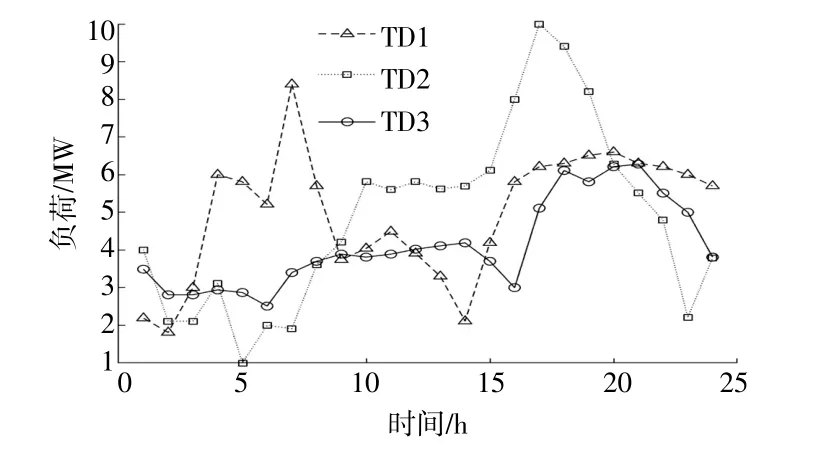
图5 负荷预测曲线Fig.5 Prediction power of load

运用CPU为Core i9-12900HX，主频为3.6 GHz，内存容量为16 GB的计算机进行优化仿真分析。运用matlab的yalmip+cplex工具包对所提下层模型进行优化求解。

3.2 仿真结果分析

本文设计了3种不同的场景以验证上述模型的有效性。

①DSO不参与碳市场交易。在电力交易中DSO不控制电价，将DSO与TD的交易电价设置为主网的购售电价，各TD间采取非协作的竞争策略。

②DSO不参与碳市场交易。在电力交易中DSO通过对电价进行调整优化自身利益，DSO与各TD间采取主从博弈模式。

③DSO参与碳市场交易。在电力交易中DSO通过对电价进行调整优化自身利益，DSO与各TD间采取主从博弈模式。

3.2.1 场景1，2对比结果分析

在场景1，2下，DSO制定的各TD与DSO的交易电价如图6所示。

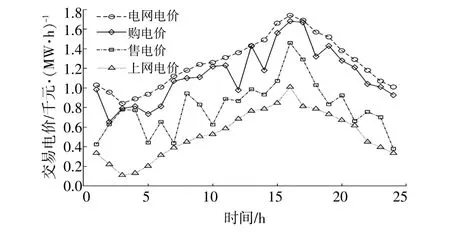
图6 交易电价Fig.6 Trading price

在图6制定的电价下，各TD根据自身利益需求调整内部DER的出力。根据各时刻自身内部发电量和用电量是否平衡，可将TD划分为“富电”、“缺电”和“平衡”3种状态。在某个时刻，处于“富电”的TD会将富余的电量出售给DSO，以获取收益，降低运行成本；处于“缺电”的TD会向DSO购买缺额的电量，以满足自身负荷用电需求；处于“平衡”的TD不须购买或者出售电量。用交易电量的多少描述TD与DSO之间的能量交易，当TD向DSO购买电量时取值为正。当交易电量大于0时，表示该TD有功率缺额，向DSO购电；当交易电量小于0时，表示该TD电量富余，售电给DSO；当交易电量等于0时，表示该TD不与DSO进行能量交易。交易电量的9种取值情况分别对应上述TD的3种状态。场景1，2下各TD与DSO交易电量如图7所示，TD的3种状态在图7中得以表现。

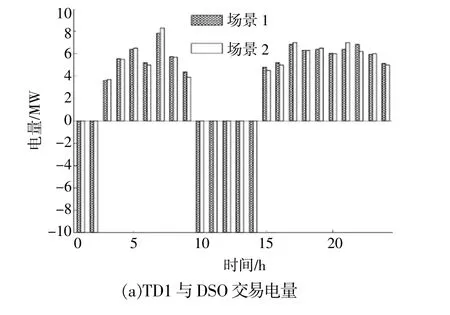
图7 场景1，2下各TD与DSO交易电量Fig.7 Trading power between TDs and DSO in subscenario 1 and 2

根据式（2），在对各TD与DSO交易的电量进行汇总后，DSO会根据下辖TD整体能否满足功率平衡来判断是否需要与电力市场进行电能交易。根据式（3），DSO与电力市场的交易电量即为各TD与DSO购电量之和减去售电量之和，因此可求出DSO与TD总交易电量。场景1，2下DSO与TD的交易电量如图8（a）所示。DSO会优先将“富电”TD富余的电能出售给“缺电”TD以弥补缺额的电能，这部分来自于TD并通过DSO用于TD的电能即为TD之间的“共享电量”。在某时刻，当＞0时，共享电量为当＜0时，共享电量为。场景1，2下各TD之间的共享电量如图8（b）所示。

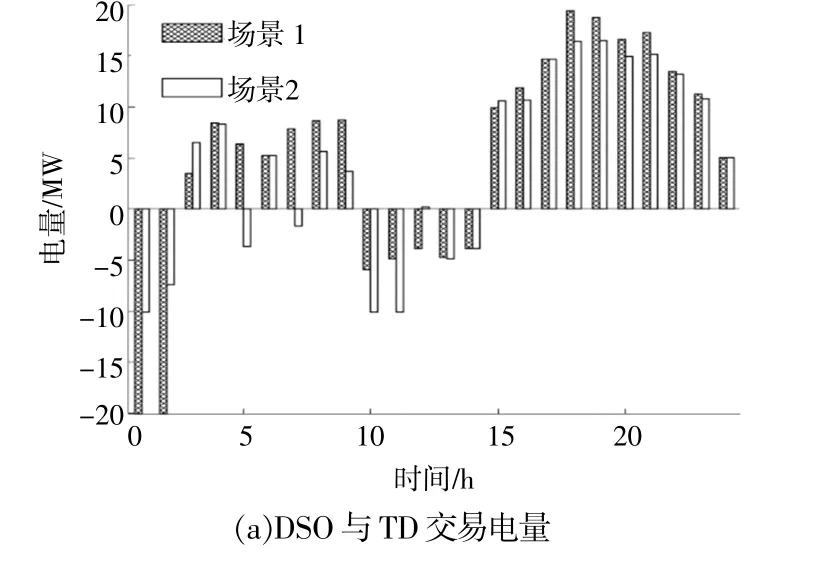
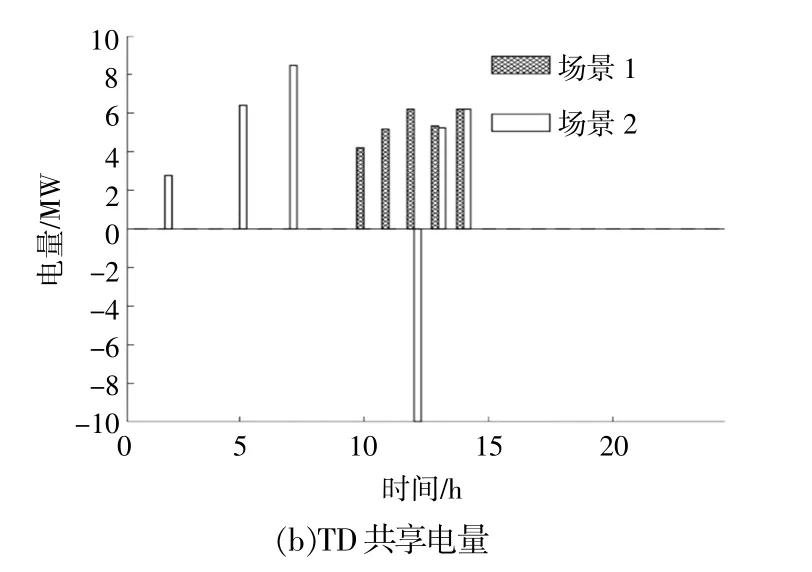
图8 场景1，2下DSO与所有TD的交易电量以及TD间的共享电量Fig.8 Trading power between DSO and all TDs and shared power between TDs

由图7可以看出，在场景1的第2小时时段，TD1，TD2分别售出10 MW的电能给DSO。根据式（2）可得TD与DSO的交易电量为-20 MW，根据式（3）可得TD之间的共享电量为0 MW。在场景2下，TD1售出10 MW的电能给DSO，TD3从DSO购买了2.8 MW的电能。根据式（2）可得DSO与TD交易电量为-7.2 MW，根据式（3）可得TD之间的共享电量为2.8 MW。在场景1的第12小时时段，TD1售出10 MW的电能给DSO，TD2从DSO购买6 MW的电能。根据式（2）可得DSO与TD交易电量为-4 MW，根据式（3）可得TD之间的共享电量为6 MW。在场景2下，TD1售出10 MW的电能给DSO，TD2从DSO购买了6 MW的电能，TD3从DSO购买了4 MW的电能。根据式（2）可得DSO与TD交易电量为0 MW，根据式（3）可得TD之间的交易电量为-10 MW。以上结果可以从图8得到验证。

比较两种场景的TD共享电量可以看出，在场景2下，TD响应DSO的动态电价并实施能源管理优化策略后，TD之间的共享电量与共享时长比场景1有显著的增长。因此，DSO向电力市场购买的电量减少了，获得的利润有所增长。

场景1，2下DSO和TD的效益如表3所示。当数值为正时表示运行成本，为负时表示利润。由表3可以看出，在场景2下，DSO能够通过优化配电网内部交易电价，显著提高自身的利润；同时，因为DSO制定的内部购电价不会超过电力市场上的电网电价，内部售电价不低于电力市场上的上网电价，所以TD的成本费用也相应减少。

表3 场景1，2下TD和DSO的效益Table 3 Benefits of TD and DSO in Scenarios 1 and 2 千元

结合图6～8，分析两种场景下运营商制定的动态交易电价和各TD与DSO交易电量之间的关系，整体上可以分为以下3类情况。

第一类是完全供不应求，典型时段如20，21，22时段。在这些时段中3个TD均处于“缺电”的状态，没有多余的电能实现跨台区共享。为了解决配网内电能不足的问题，DSO只能通过电力市场向主网购电，然后TD向DSO购电满足自身需求。DSO为了减少损失，会制定较高的配网内售电价格，从图6可以看出，这些时段的售电价均接近于电网电价。

第二类是整体供不应求，典型时段如15，16，17时段。在这些时段中存在多种状态TD，但整体上还是供不应求，DSO仍然要向主网购电满足需求。从图6可以看出，此时DSO仍然会给TD制定较高的售电价格，但是比起第一类情况要低一些，同时还会制定较高的购电电价，引导“富电”TD多售电，满足“缺电”TD需求，以减少DSO从电力市场购电。

第三类是整体供过于求，典型时段如1，2，10，11时段。在这些时段中同样存在多种状态TD，但整体上是供过于求，DSO会将多余电能卖到电力市场以获取利益。由于此时电能充沛，DSO会制定较低的售电价格，吸引“缺电”TD和“平衡”TD购电，实现自身更多利益。

3.2.2 场景2，3对比结果分析

在场景2下，DSO未参与碳市场交易，此时尚未计及碳排放成本。在场景3下，由于DSO在电力交易的基础上还参与了碳市场交易，需要在兼顾电能交易收益的同时兼顾发电的清洁成本，平衡电能需求与碳排放。本文分别设置了隶属于场景3的3种子场景，各子场景对应的碳价λC和单位CCER的交易价格λCCER组合如表4所示。台区1在场景2及场景3中子场景1～3对应的风电、光伏出力曲线分别如图9，10所示，其余台区内的风光出力见图11～14。

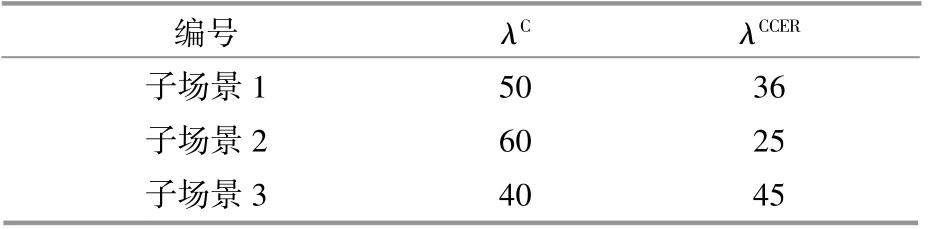
表4 不同子场景下的碳价和单位CCER价格Table 4 The price of carbon and unit CCER in different sub-scenarios 元/t

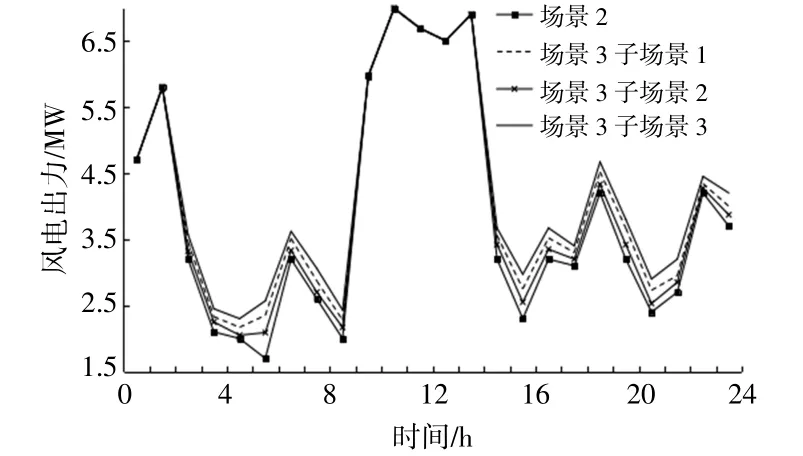
图9 不同场景下台区1内WT功率曲线Fig.9 Power output curve under different scenarios of WT in DT1

由图9可以看出，在3～9，15～24时段内，场景3的子场景3对应的风电出力最大，子场景1对应的风电出力最小。由表4可知，子场景3所对应的碳价λC最高，而单位CCER交易价格λCCER最低，造成该场景下台区通过调用分布式MT发电的碳排放成本高，而通过调用分布式可再生能源发电在碳市场中可以获得较多的补贴。因此，在子场景3下，台区1倾向于调用分布式MT，PV发电，此现象同样出现在其余台区中，具体见图11～14。由图10可知，在6～9，15～19时段内，场景3的子场景3对应的光伏出力最大，子场景1对应的光伏出力最小，这一现象同样是由上述原因所导致的。

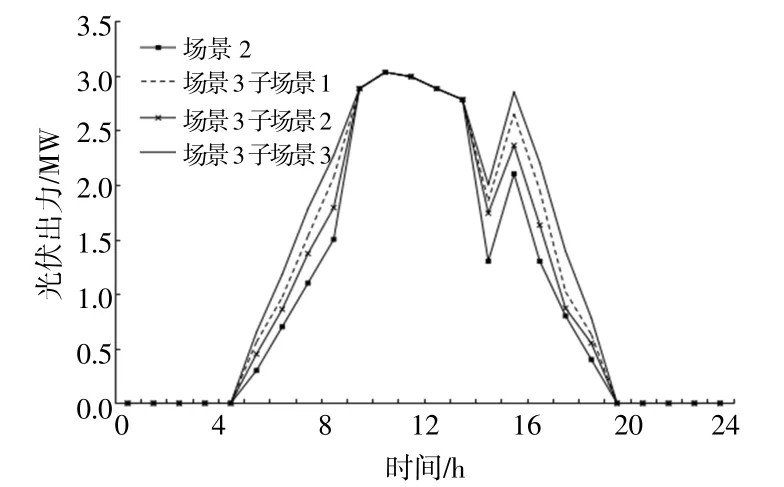
图10 不同场景下台区1内PV功率曲线Fig.10 Power output curve under different scenarios of PV in DT1

图11 不同场景下台区2内WT功率曲线Fig.11 Power output curve under different scenarios of WT in DT2

图12 不同场景下台区2内PV功率曲线Fig.12 Power output curve under different scenarios of PV in DT2

图13 不同场景下台区3内WT功率曲线Fig.13 Power output curve under different scenarios of WT in DT3

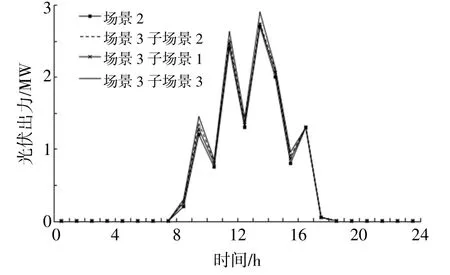
图14 不同场景下台区3内PV功率曲线Fig.14 Power output curve under different scenarios of PV in DT3

由图9，10还可以看出，在场景2下风光出力均小于场景3中各子场景下的风光出力，这是因为场景2中DSO不参与碳市场交易，未能调动各台区内可再生能源出力的积极性。由此可见，参与碳市场交易有助于调整配电侧分布式发电能源结构，刺激台区调动内部清洁能源发电。由图9可知，在1～2，10～14时段内，各场景下风电出力相同。而图10显示，在10～14时段内，各场景下光伏出力相同。这是由于在上述时段内，台区1通过向DSO售电获利，此时分布式可再生能源满发以满足台区1向DSO售电的需求。

4 结论

针对配电侧多台区运行优化问题，本文构建了主从博弈模型，将DSO和所辖TD分别作为博弈的领导者与跟随者，实现了领导、跟随双方利益的优化。针对分布式可再生能源出力的不确定性，本文采用CVaR理论进行量化，规避了风光出力不确定性造成的运行损失。此外，本文进一步将碳市场收益加入DSO效益模型，通过加入碳市场交易刺激所辖台区内可再生能源出力，降低发电碳排放成本，实现电碳市场收益综合优化。最后，通过算例验证本文所建模型的有效性，得出以下结论。

①依托主从博弈模型，DSO能够执行动态定价策略引导TD进行电能交易，并使双方在此过程中均能获得最大收益。

②通过运用CVaR模型量化可再生能源出力的不确定性，降低了弃风、弃光成本。

③将碳排放成本加入DSO效益模型，能有效刺激TD内可再生能源出力，提升能源清洁性。

由于新型电力系统建设不断完善，分布式可再生能源在配网侧的接入比将不断提升，未来将进一步研究配电侧高比例可再生能源接入下的电碳协同市场机制优化问题，并针对各类可再生能源进行精细化建模，以确保系统安全高效运行。