基于最小二乘法的平面度测量系统设计
彭 壮,颜 强,朱 岩,罗 汉,解 鏊
(湖南云箭集团有限公司 湖南 长沙 410100)
0 引言
在现代制造业中,平面度是一个重要的表面质量指标,是指被测实际表面所有测量点相对其最小二乘平面的变动量[1],用于评估零件表面的平整程度。 平面度误差的评定方法主要有三点法、对角线法、最小区域法和最小二乘法等。 最小二乘法是一种基于数学模型的优化方法,通过最小化测量残差的平方和来拟合实际测量数据与理想模型之间的关系,来评估零件表面的平整度[2]。 由于最小二乘法具有良好的数学性质和可靠的测量结果,被广泛应用于各个领域的测量任务。 倍福可编程逻辑控制器(programmable logic controller,PLC)是一种先进的自动化控制设备,具有高精度和高可靠性的特点,广泛应用于工业制造领域[3]。 本文设计一种基于最小二乘法的平面度测量系统,用于实现高效而准确的平面度测量,取代人工测量,大大提高了平面度测量的精度和稳定性。
1 算法原理
最小二乘法又称为最小平方法。 它是一种寻找数据的最佳函数的匹配方法[4]。 它常用于数据分析和回归分析,可以帮助确定未知数据,并使得这些数据与实际数据之间的误差的平方和最小化。 它能在确定的数据点集合中,通过拟合一个函数模型,使得该函数与数据点之间的误差最小化。 首先,可以假设一个函数模型,根据给定的数据点计算该函数模型与实际数据之间的误差,然后,通过最小化这些误差的平方和来确定函数模型中的参数。最后,最小二乘法的应用可以扩展到评估平面度误差。 平面度误差是指在表面测量中,评估表面平整度的一种方法。 最小二乘法可以用来拟合一个平面,作为评估基准平面,并计算实际表面与该基准平面之间的平面度误差[5]。最小二乘平面的建立方法为:
设最小二乘平面方程为式(1)所示:
式(1)中,A、B、C为方程系数。 只要确定了A、B、C的值,就确定了平面方程。
设实测工件平面上各点的坐标为Pi(xi,yi,zi)(i =1,2,…,k)。 根据最小二乘法原理可知,实测平面上各点的值Pi(xi,yi,zi) 与最小二乘平面上各点的Z向距离平方和为最小。Z向距离平方和方程为式(2)所示:
根据极值原理,要使F的值为最小,则要使F对A、B、C的偏导值为零。 即式(3)所示:
整理矩阵化可得式(4):
则可解得最小二乘平面方程系数A、B、C为式(5)所示:
进一步整理可得式(6):
其中,
根据以上求解得到A、B、C的值就建立了最小二乘平面方程,分别求出平面上各测点对最小二乘平面的偏移量ZDi=Axi+Byi+C-zi,判断找出Di的最大值Dmax和最小值Dmin,则被测平面的平面度误差为式(8)所示:
2 系统设计实现
2.1 硬件设计
(1)PLC 单元选择。 此测量系统开发平台采用倍福可编程逻辑控制器PLC 平台CX-5130。 CX-5130 是倍福公司推出的一款基于PC 的PLC。 它是一款高性能、高可靠性的嵌入式控制器,用于工业自动化和控制系统。 它采用Intel Atom 双核处理器和高速内存,提供强大的计算能力,适用于需要处理复杂数据和实时反馈的应用。 它的运算处理器频率为1.75GHz,主内存为4GB,具有多种接口,包括以太网、USB、串口等,方便与其他设备进行通信和连接。 它还支持多种外部模块和扩展卡的添加,支持EtherCAT 现场总线。 EtherCAT 是一种高性能的现场总线通信协议,用于实时控制和自动化领域。 它基于以太网技术,通过一个主站和多个从站之间的通信,实现实时传输控制数据和实时反馈数据。 EtherCAT 的通信速度非常快,可达到100 Mbps 以上,同时具备很低的通信延迟。 这使得它适用于需要高实时性的工业自动化系统。EtherCAT 的拓扑结构灵活,支持线性、环形、星形以及混合拓扑结构。 这使得布线和扩展系统变得更加简单,可以根据需要增加或减少从站。 EtherCAT 支持标准以太网硬件和协议,可以与其他以太网设备进行集成。 此外,EtherCAT 还提供了大量的设备配置和通信诊断工具,方便系统的开发和调试[6-7]。
(2)传感器选择。 测量传感器选择欧姆龙激光位移传感器。 通过激光反射测量物体位移和距离。 测量范围为30±2 mm,重复精度高达±2 um。 支持EtherCAT 现场总线。
(3)运动机构设计。 结构配备有高精度的定位夹具和高精度全闭环松下伺服驱动模组,来实现工件的移位与传感器的移位。 结构采用双测量头、单X 轴和双Y 轴的结构架构,实现一次测量2 个工件的同时还能进行另一工位的上下料,最大限度提高运行效率。
(4)存储器设计。 考虑到PLC 主内存偏小,设计增加外部扩展存储器。 采用了金士顿闪存盘/64G 移动U 盘作为存储媒介,以实现大容量生产数据的记录。 同时,为了确保数据的安全性和稳定性,倍福PLC 还配备了不间断电源(uninterruptible power supply, UPS),它能在电网供电异常或断电时,为PLC 等设备提供一定时间可靠的供电,以保证系统的稳定运行和数据存储的完整性。
PLC 平台通过EtherCAT 现场总线控制伺服驱动和激光传感器。 测量系统结构如图1 所示。
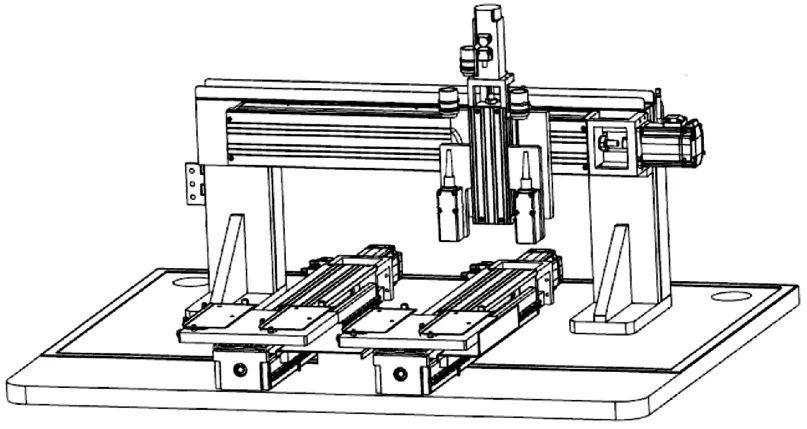
图1 测量系统结构图
2.2 软件设计
TwinCAT ( The Windows Control and Automation Technology)是倍福公司开发的一款用于工业自动化系统的软件开发环境。 它基于Windows 操作系统和标准的IEC 61131-3 编程语言,为用户提供了一个强大而灵活的平台,用于开发、编程和配置工控系统。 IEC 61131-3 标准的编程语言是国际标准语言,包括梯形图、指令列表、功能块图、结构化文本和顺序功能图等。 用户可以根据自己的需求选择合适的编程语言。 该系统采用结构化文本语言来进行系统控制流程的开发。
系统控制流程为:首先,PLC 通过控制X 轴和双Y 轴伺服驱动将传感器瞄准工件上的测量位置,并获取激光传感器的实时测量值。 然后,根据记录的测点坐标位置以及激光测量值来计算最小二乘平面系数、测点至最小二乘平面的平面度误差。 最后,判断平面度误差是否在允许范围内,并输出OK/NG 结果。 控制流程如图2 所示。
根据以上流程得到被测工件上10 个均匀分布的采样点P1~P10 的X、Y、Z位置坐标,通过程序算法计算得到最小二乘平面方程系数A、B、C和被测工件平面度误差结果。 坐标点位如表1 所示。
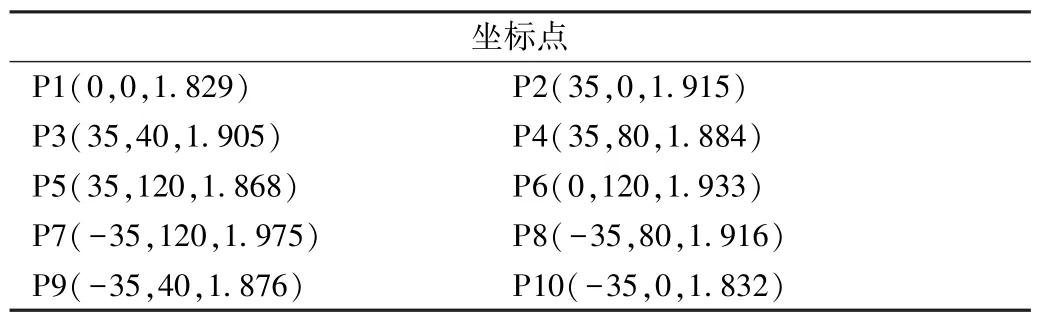
表1 测量点坐标
程序计算解得最小二乘平面方程系数A、B、C分别为-0.000 096 428,0.000 533 62,1.861 282 758。 根据求解的最小二乘平面方程系数A、B、C,即可计算出此被测工件的平整度误差结果为0.111 mm。
3 应用实例
本研究针对某制造厂的金属框产品进行了相关性的测试。 通过采用10 个均匀分布的采样点测量方式,分别得到32 件不同的金属框工件的本系统的测量数据和专用三位测量仪的测量数据。 其相关性测量结果如表2 所示。

表2 相关性结果
数据显示,此测量系统的重复精度±0.01 mm,其测量结果与专用三维测量仪测量结果基本一致。 测量周期时间1.75 s/pc,解决了人工测量速度慢、误判率高的问题。
4 结语
本文基于最小二乘法设计的平面度测量系统成功应用。 经过应用证明,系统运行可靠性和生产效率高。 在设计与使用中,本测量系统具有以下特点:
(1)通过最小二乘法的拟合算法,能精确、高效地测定平面的平面度误差,测量精度达±0.01 mm,有效地提高了平面度测量的精度和稳定性,解决手工速度慢、准确性差等问题。 实现高效的自动化生产。
(2)采用倍福PLC 运动控制器作为平台,扫描周期快,总线连接控制方便,控制精度高,开发周期短,功能强大,接线少,易于使用和维护。
(3)结构硬件配置遵循简单化、模块化的原则,提高了整个系统的可扩展性、可靠性和可维护性。

