二维水流数学模型在船厂工程防洪影响评价中的应用

邱居华，李 阳，朱士江，王海银

(1.湖北欣瑞工程咨询有限公司，湖北 宜昌 443000；2.湖北昊源建设工程有限公司，湖北 宜昌 443000；3.三峡大学，湖北 宜昌 443000)

1 工程概况

本船厂工程位于三峡大坝和葛洲坝两大水利枢纽之间，长江右岸(葛洲坝库区南岸)南沱村，距离三峡大坝下游约15.0 km。工程河段水位、流量条件直接受水利枢纽调度影响，有实测数据。

本船厂工程生产场地约33 335 m2，船台8个(其中有4个为混凝土地面，另外4个为沙土地面)，舾装码头1座，占用长江水域岸线长度约300 m，厂区分为加工区、制作区、仓储区、人员办公区、混凝土地面船舶修造区、沙土地面船舶修造区等；生产、测量设备及检测设备近400台(套)，主要生产活动为修船和造船。

2 二维水流数学模型

近年来，二维水流数学模型被运用于各种涉河建筑物的防洪影响评价计算，为工程建设提供技术支撑[1]。石少山[2]使用二维水流数学模型对亲水广场进行防洪评价计算，王丽君[3]使用二维水流数学模型对输电线路工程进行防洪评价计算，王鑫等[4-6]使用二维水流数学模型对跨河大桥工程进行防洪评价计算，盛建兴[7]、曹开兴[8]等使用二维水流数学模型对码头工程进行防洪评价计算。

对于复杂天然河道水流运动的数值模拟，为了克服计算区域边界复杂的困难，同时也为了提高数值计算成果的精度，多采用基于曲线网格的坐标变换方法，使计算网格贴合曲折的河道边界。其中正交曲线变换和一般(非正交)曲线变换方法是两种最常用的方法。与正交曲线变换相比，一般曲线变换不受计算网格必须严格正交的限制，网格生成也较灵活。因此本次采用一般曲线坐标变换方法实现计算边界与物理边界的准确耦合。

2.1 模型计算控制方程

考虑侧向入汇流影响，笛卡尔坐标系下平面二维水流数学模型的控制方程如下：

水流连续方程如式(1)：

h=n+d

(1)

x方向水流运动方程如式(2)：

(2)

式中：f为柯氏力系数；η为河底高程，m；Pa为当地大气压，MPa；g为重力加速度，m/s2；ρ为水的密度，kg/m3；ρ0为参照水密度，kg/m3；τsx、τbx分别为风场摩擦力在x、y上的分量，MPa；sxx、sxy分别为辐射应力分量，MPa；Txx、Txy为水平黏滞力应力分量，MPa；uS为源项x方向水流流速，m/s。

y方向水流运动方程如式(3)：

(3)

式中：τsy、τby分别为底床摩擦力在x、y上的分量；syx、syy分别为辐射应力分量；Tyy为水平黏滞力应力分量；vS为源项y方向水流流速，m/s。

2.2 模型方程离散和求解

MIKE21模型的数值解法主要有空间离散方程组成，计算区域的空间离散是用有限体积法(Finite Volume Method)，其求解方式是将计算区域划分成不重复的控制单元，单元理论上可以是任意形状的多边形，但在这里一般分解成三角形和四边形单元。

浅水方程组的通用形式如式(4)：

(4)

式中：U为守恒型物理向量；F(U)为通量向量，S(U)为源项S的微分函数表达式。

在笛卡尔坐标系中，二维浅水方程组如式(5)：

(5)

式中：Fx、Fy分别为F(通量向量)在x和y方向的分量；I、V分别为无黏性通量和黏性通量。各个参数的计算如式(6)～式(11)：

(6)

(7)

(8)

(9)

(10)

(11)

式中：A为过水面积，m2。

对上述浅水方程的的第i个单元进行积分，选用Gauss原理重写后见式(12)：

(12)

式中：Ai为单元Ωi的面积；Γi为单元的边界；ds、dΩ分别为沿着Γi、Ai边界的积分变量；n为糙率。

式(12)运用了单点求积法来计算面积的积分，该求积点位于单元的质点，同时运用中点求积法来计算边界积分，如式(13)：

(13)

式中：Ui为第i个单元的U的平均值，并位于单元中心；Si为第i个单元的S的平均值，并位于单元中心；NS为单元的边界数ΔΓj为第j个单元的长度。

3 数学模型验证

模型验证计算的目的在于检验数学模型计算方法的可行性，根据实测资料确定模型中相关参数的取值，并检验其精度。本次主要根据水面线和垂线平均流速分布资料对模型参数进行调试。

3.1 模型计算范围及边界处理

(1)工程河段地形图。采用2016年11月实测工程河段1/2000河道地形图。

(2)水文资料。采用2014年9月3日(Q=45 100 m3/s)一组测验水面线及断面垂线平均流速分布资料，共验证4个水位点水位和4个断面垂线流速分布情况，验证水位点及流速分布断面位置见图1～图2。

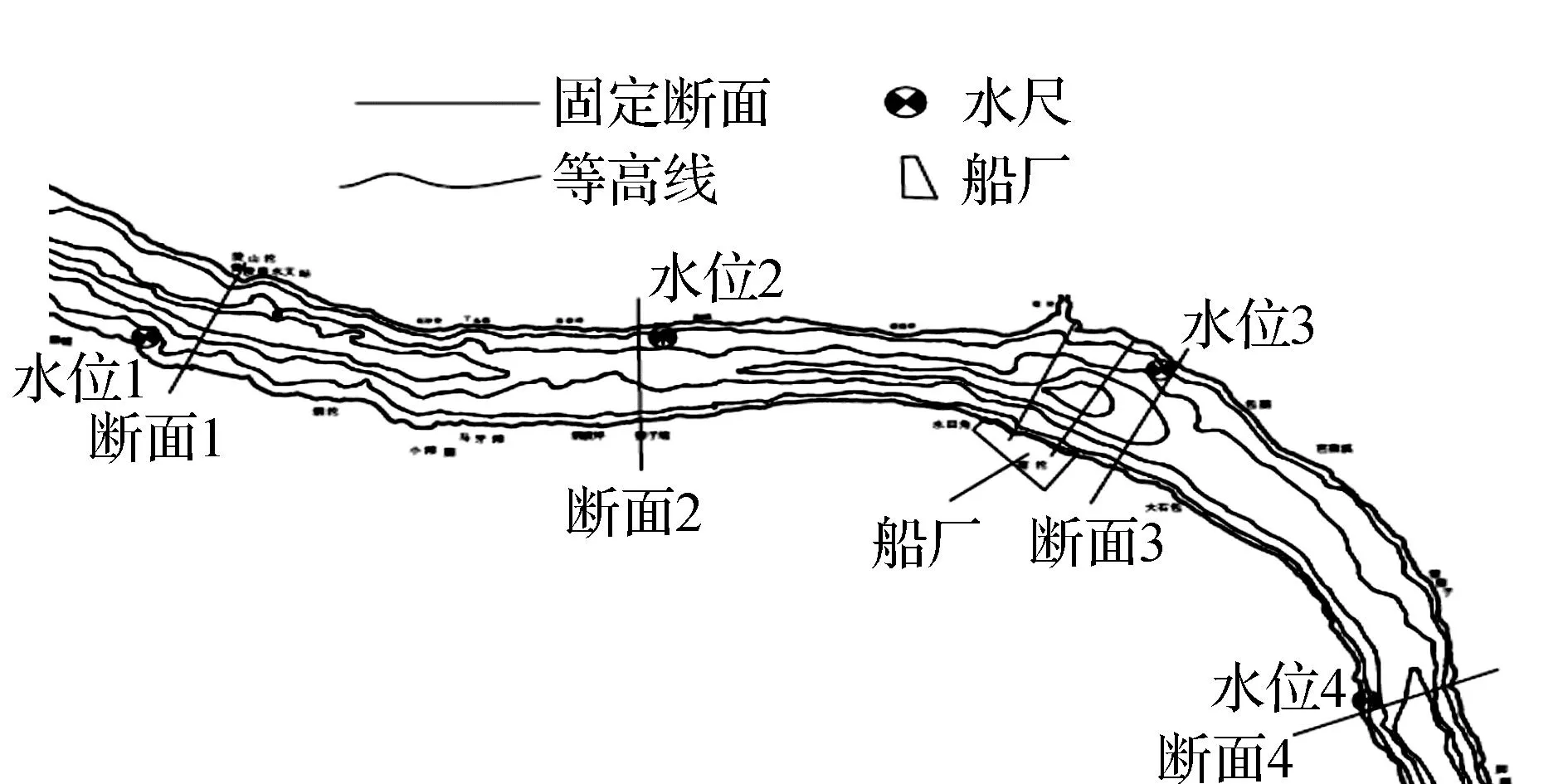
图1 数学模型计算区域地形概况

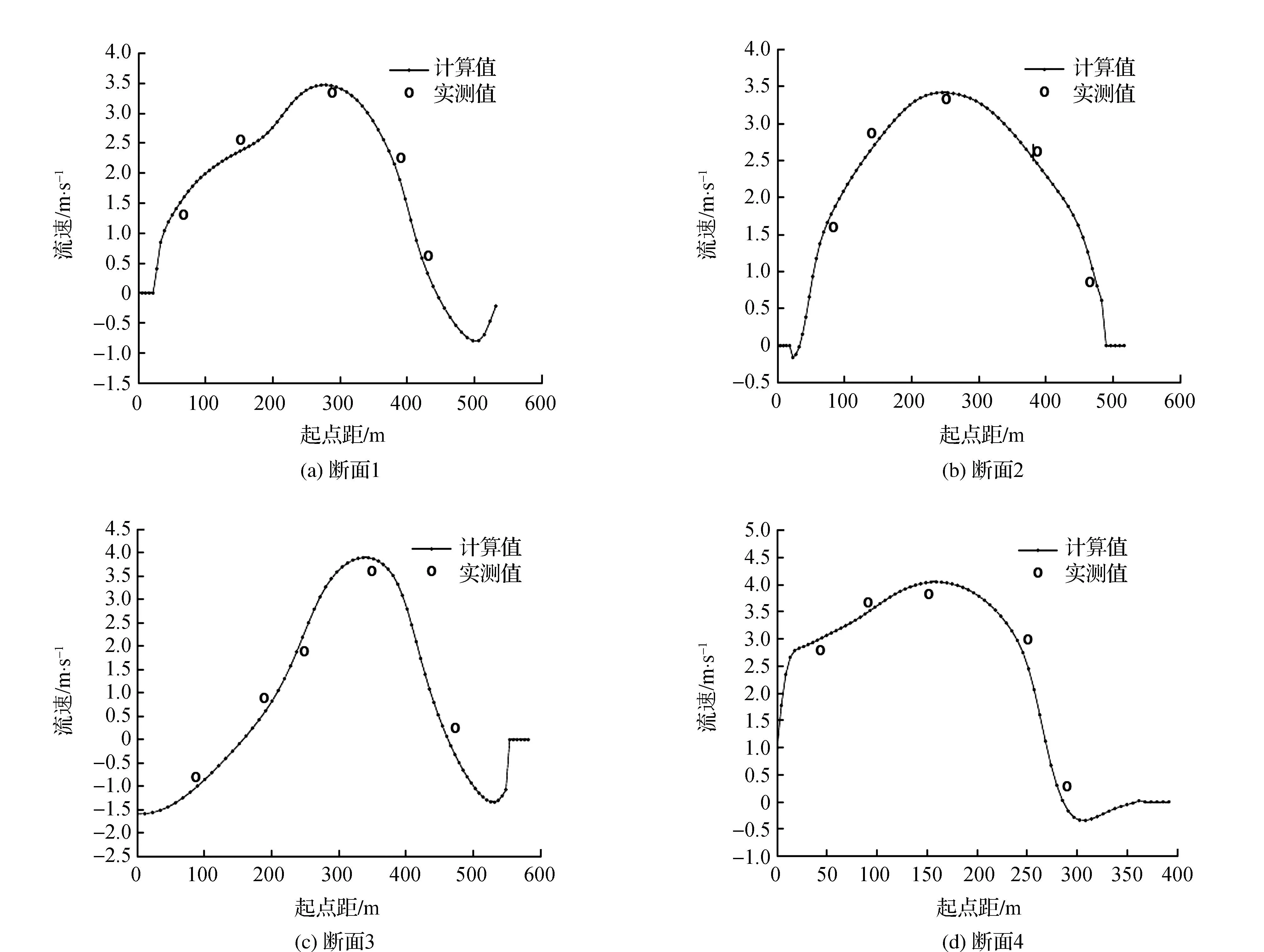
图2 各断面流速分布验证(Q=45 100 m3/s)

(3)边界条件处理。平面二维水流模型中，边界条件通常包括河道进出口边界、岸边界及动边界等。本模型中对上述边界分别做以下处理：①进口边界。根据已知进口全断面流量，给定入流单宽流量沿断面的横向分布。②出口边界。给定出口断面的水位。③地形边界。取河道地形图外边线为计算的岸边界，给定其一个比较高的高程令其流速为0 m/s，以保证计算区域的封闭。④动边界。

本模型采用“冻结”法进行动边界处理，即根据水位结点处河底高程来判断该网格单元是否露出水面。若不露出，糙率取正常值；反之，更改单元的糙率(n取1010量级)。为不影响水流控制方程的求解，在露出水面的结点处需给定一个薄水层，一般给定其厚度为0.5 cm。

3.2 模型验证计算成果

模型计算水位成果与实测成果比较见表1。模型计算水位与实测水位基本吻合，其最大相差为0.2 cm。

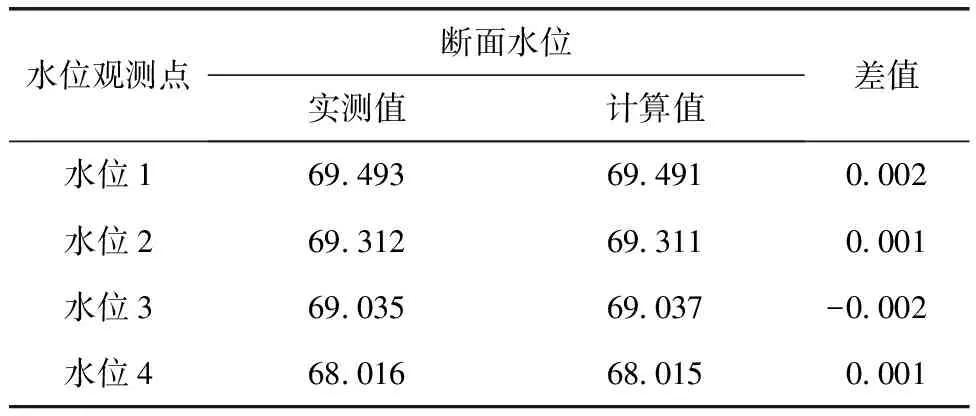
表1 水位验证计算成果 m

根据实测水文资料综合调试，得到该河段糙率变化范围为主槽n=0.030～0.036，滩地糙率n=0.035～0.046。

图1～图2给出了工程河段4个流速断面垂线流速分布验证成果，计算与实测流速大小和沿河宽分布情况基本一致，两者误差一般<5.0%。图3为根据验证条件计算得到的河段流场。模型计算得到的流场变化平顺，洪枯水条件下水流运动特征明显，滩槽水流运动区分合理，水流运动形态与河道地形变化情况符合较好。

综合分析以上验证计算成果，所采用的数学模型能较好地模拟工程河段水流运动特性，验证计算成果与实测成果吻合较好，表明数学模型的计算方法正确，模型中相关参数取值合理，可以用于船厂工程影响河道水位及流速的计算分析。

4 案例应用与分析计算

4.1 水文条件

为评价船厂工程修建后对工程河段行洪的影响，计算时主要针对长江汛期高水位条件，考虑100 a一遇设计洪水56 700 m3/s流量工况，还考虑了汛期维持下游通航的三峡控泄流量45 000 m3/s、汛期常遇流量30 000 m3/s三种工况，具体计算条件见表2。

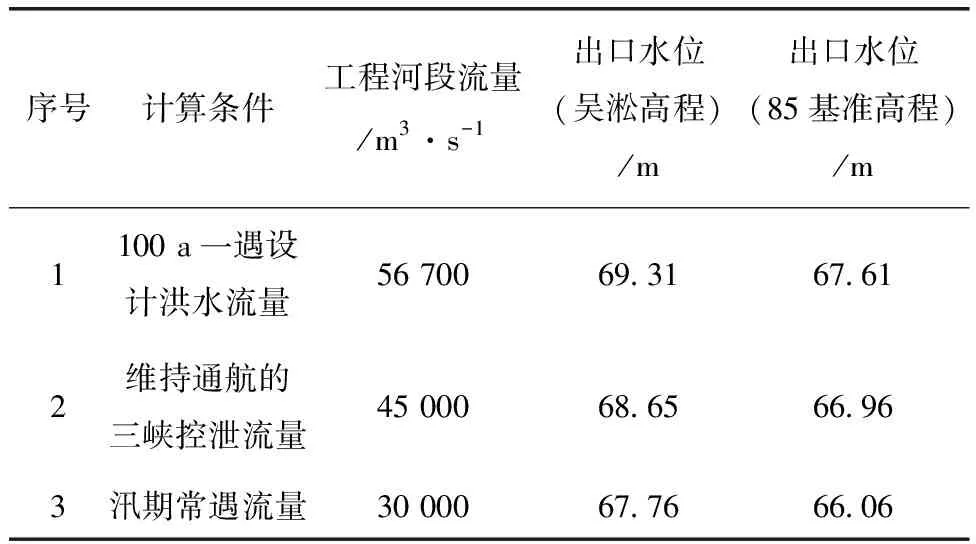
表2 各工况计算条件

4.2 工程概化

根据船厂工程设计方案，船厂工程主要阻水部分主要为：车间平台、船体放置平台、实体坡道、架空下河坡道、坡道前沿的趸船等。为反映工程对河道水流运动的影响，在计算过程中通过局部糙率调整的方法进行工程概化。具体为：

(1)对于实体坡道，主要是通过修改局部地形来反映工程的影响。

(2)对于架空坡道按工程量计算各水位下的阻水面积，对于趸船按照船体尺寸及吃水计算阻水面积，根据以上两项计算成果确定工程后的河道过水面积值，通过公式将阻水转换为局部糙率值。

(3)局部糙率计算方法：局部阻力系数ζ计算如式(14)：

ζ=0.5(1-A工程后/A工程前)

(14)

式中：A工程后、A工程前分别为工程后、工程前的过水面积，m2。

为便于计算，将局部阻力系数转化为糙率的形式如式(15)：

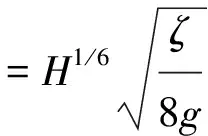
(15)

式中：n阻为糙率；H为吃水深度，m。

最后得到施工区域所在网格的局部综合糙率系数n为如式(16)：

(16)

式中：n工程前为工程前的糙率。

4.3 计算成果分析

4.3.1 工程后断面缩窄率

为了了解船厂工程区域内工程前后横断面变化及断面过水面积缩窄情况，根据船厂工程的平面布置，选择船厂车间平台及船体放置平台作为代表断面进行分析研究。以2016年11月地形图为基础，计算了船厂工程后的断面缩窄率见表3。

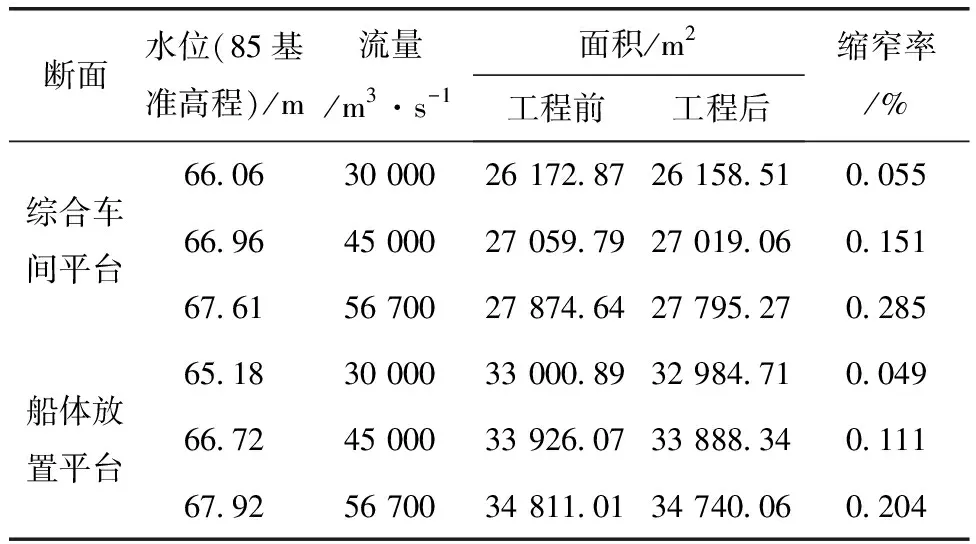
表3 船厂面积缩窄率计算成果

计算表明，工程后在各设计洪水位下，工程区域河道的横断面过水面积均略有减小，随着水位不同面积缩窄率略有不同，船厂的面积缩窄率均<1.000%。遇100 a一遇的洪水时，船厂最大面积缩窄率约为0.285%；遇流量30 000 m3/s、45 000 m3/s洪水时最大面积缩窄率变化不大，变化大小幅度分别为0.055%、0.151%。满足《长江流域和澜沧江以西(含澜沧江)区域河湖管理范围内建设项目工程建设方案洪水影响审查技术标准》(T/CTESGS 02—2022长江技术经济学会，2023.01.01)的要求。

4.3.2 工程对水位影响分析

船厂工程建设后，河道过流断面被束窄，河槽水位随之出现一定调整，模型计算表明：上游不同来流条件下，船厂工程引起的河道水位变化分布规律大致相似，均呈现出上游局部水位抬高，下游局部水位降低；且水位变化影响范围和影响程度随流量增加有所增加，但总体变化幅度均不大。工程前后水位变化见表4、图4～图5。

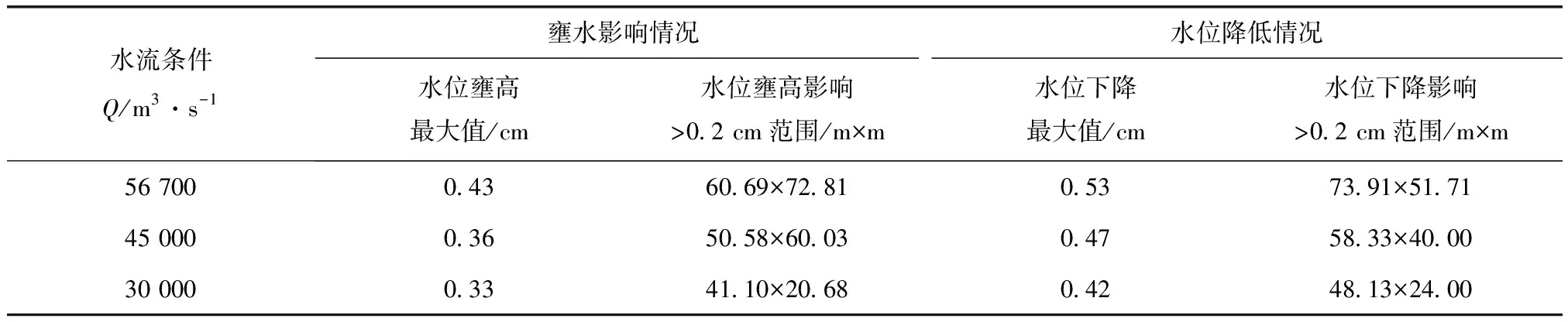
表4 工程前后水位变化计算成果

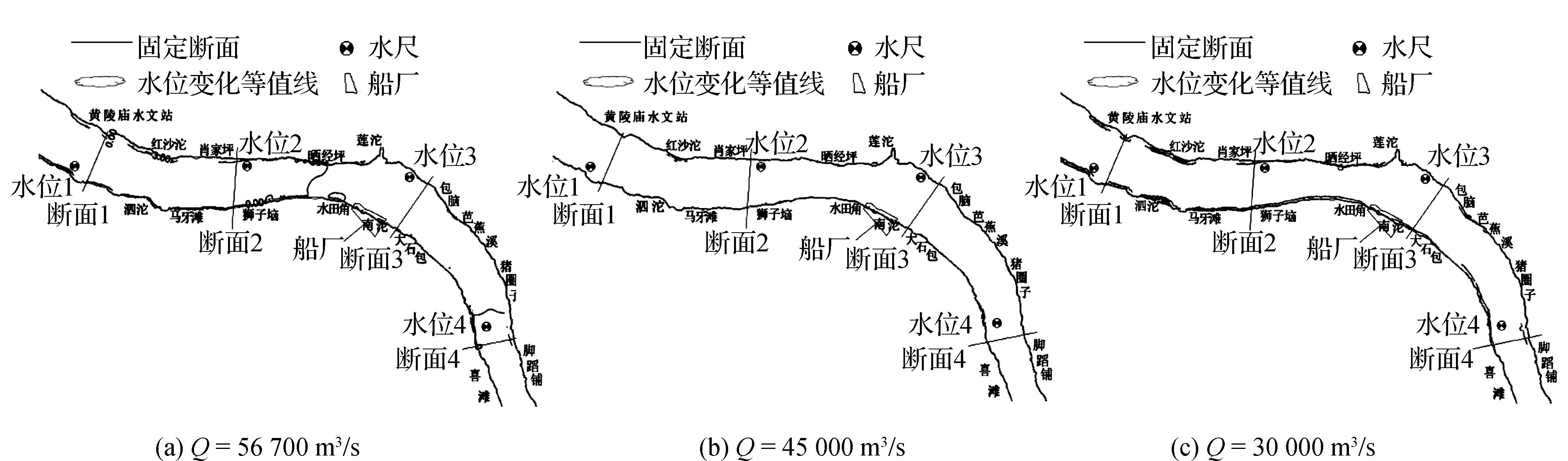
图4 评价区域水位变化等值线

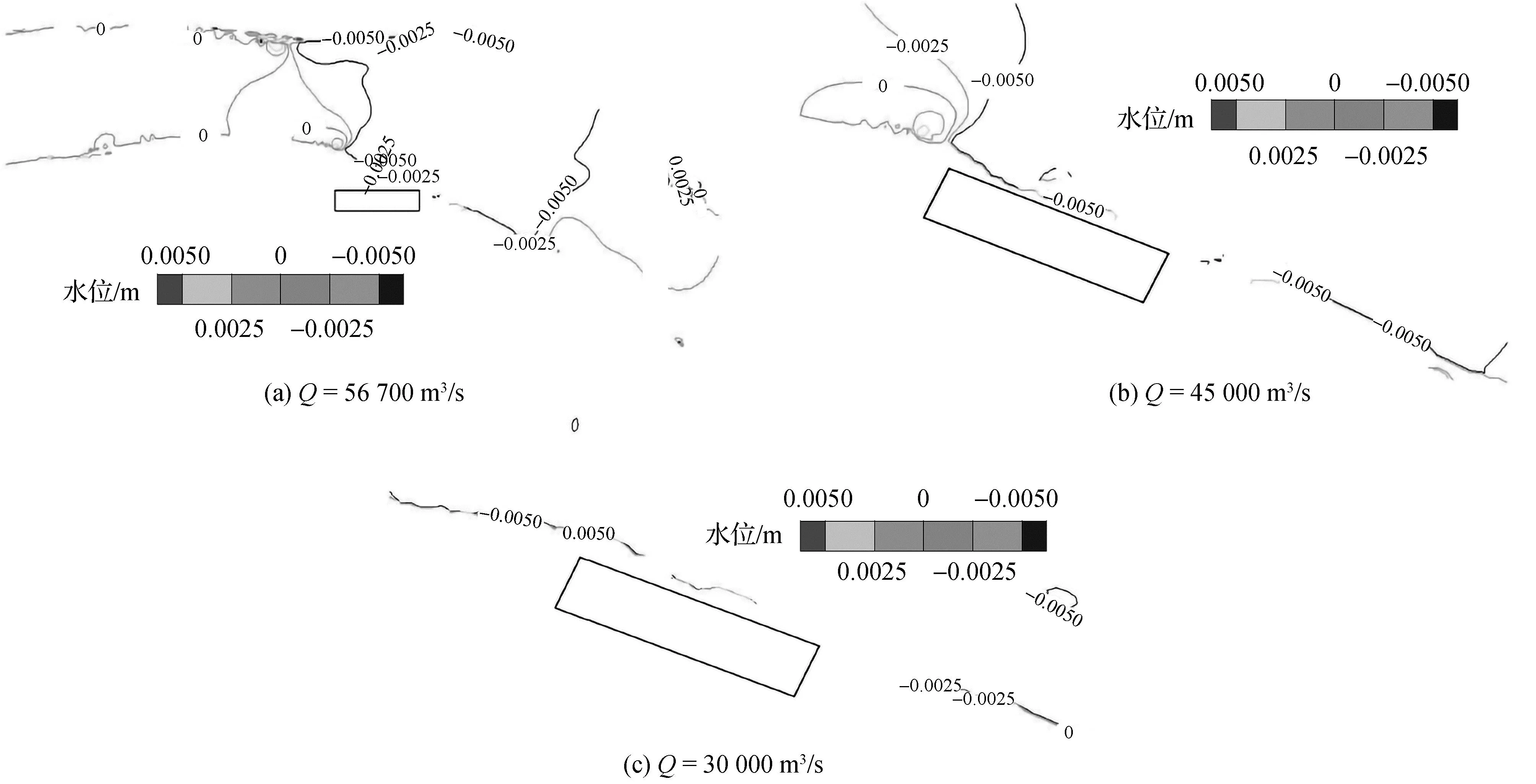
图5 船厂区域水位变化等值线

4.3.3 工程对流速影响分析

工程修建以后引起的流速变化主要集中在船厂区上下游、前沿局部区域。具体影响表现为船厂上游局部区域受阻水作用，流速表现为下降，船厂区域及其下游局部由于水流绕流紊动扩散，流速也相应下降，船厂前沿水流受工程挤压，局部流速有所增加。同时计算表明，船厂对下游流速的影响大于上游，流速减小幅度和影响范围大于流速增加幅度及影响范围，船厂对流速的影响随着流量增大而增大，但总体影响较小。船厂工程前后流速变化见表5、图6～图7。

表5 工程前后流速变化计算成果

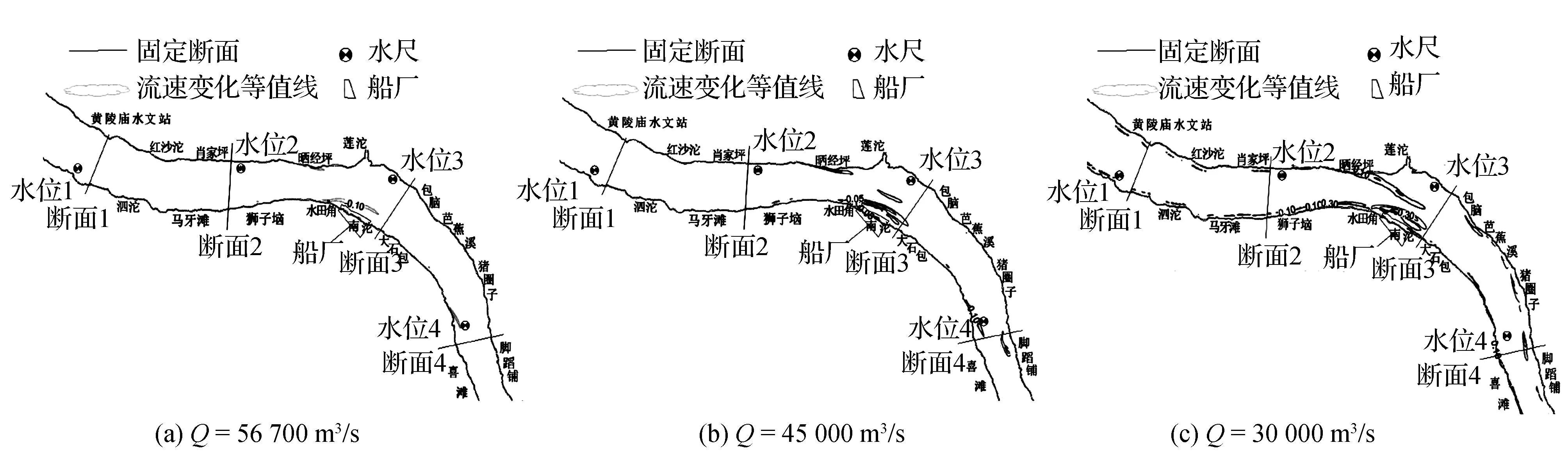
图6 评价区域流速变化等值线

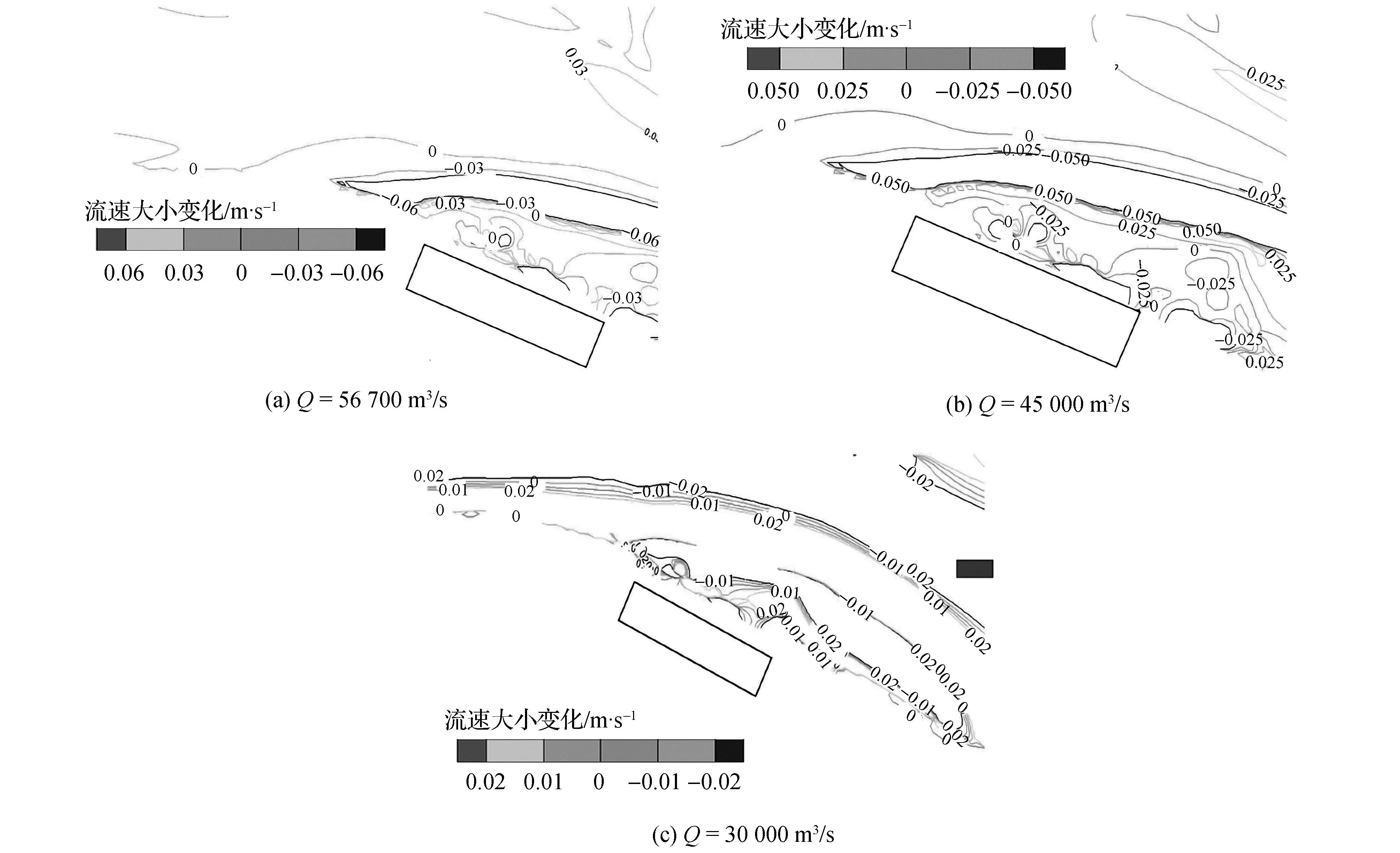
图7 船厂区域流速变化等值线

4.3.4 综合评价分析

本工程建设后，河道过流断面略被束窄，河槽水位出现小调整。模型计算表明：本工程引起的水位变化情况为船厂工程上游局部水位抬高，下游局部水位降低，汛期遭遇100 a一遇洪水时，局部最大壅水值为0.43 cm。船厂前沿流速略有增加，船厂区域流速略有减小，汛期遭遇100 a一遇洪水时，流速最大增加值为0.06 m/s。船厂工程对水位、流速的影响量和影响范围随流量增加而增大。

在工程影响范围内，本工程兴建对河道过水面积缩窄率、壅水高度、流速变化的影响较小，不会对河势及河道行洪产生明显不利的影响。

5 结 语

(1)结合水文站实测数据成果对本文计算成果进行了验证，验证计算成果与实测成果吻合较好，表明本文所采用的数学模型能较好地模拟工程河段水流运动特性，数学模型的计算方法正确，模型中相关参数取值合理，适用于船厂工程影响河道水位及流速的计算分析。

(2)通过二维水流数学模型计算分析看出，工程前后河道水动力特性和流场的变化不大，水流流态及水流流速分布无明显变化，计算成果可靠，为建设项目对防洪影响的计算与分析提供了可靠的方法，为建设项目安全运行提供了保障。