悬臂式抗滑桩桩后土拱效应及影响因素分析

周永兴

(江西省万载县安泰水利水电建筑有限公司，江西 宜春 336000)

1 工程概况

悬臂式抗滑桩是一段嵌固在岩土体，另一段出露在土体上部的一种抗滑桩类型。在边坡支护工程中，悬臂式抗滑桩桩后岩土体与桩体相互作用，使桩后土体中产生具有一定承载能力和应力传递能力的桩后土拱，进而对桩体的抗滑设计产生影响。且桩后土拱前部区域土体的破坏形式对桩前区域的安全性具有重要影响，故研究悬臂式抗滑桩支护边坡中以桩后土拱效应为主的桩-土相互作用具有重要意义。

近年来，国内外学者分别从理论分析、数值模拟、模型试验等多方面对土拱效应进行了深入的研究。Handy对土拱的形态进行描绘，首次提出土拱拱型的主应力迹线为近似悬链线。吴子树等采用物理模型试验对土拱的形成机理及条件进行了研究，认为土体自身的粘聚力和摩擦是土拱能形成的要素。张永兴等通过斜坡中悬臂式抗滑桩的模型试验，证实了以合理桩间距布置的悬臂桩的桩间土体是在端承拱的拱圈内侧开始发生破坏。

以上研究主要针对抗滑桩截面形态及桩间距等影响因素进行分析，本文从桩后土拱的主应分布出发，采用FLAC3D建立简化的悬臂式抗滑桩支护边坡三维计算模型，对桩后土体的应力、位移、桩后土拱的三维形态、桩前被动士拱的形态和应力变化及相关影响因素进行研究。为悬臂式抗滑桩应用提供参考。

2 边坡模型及约束条件

本文采用FLAC3D建立了采用悬臂式抗滑桩进行支护的简化边坡三维模型，抗滑桩发挥阻滑作用时，桩土间的相互作用受多因素影响，比较复杂。使用FLAC3D进行三维建模时先作以下假定：(1)抗滑桩截面为矩形，以实体桩模型进行数值模拟；(2)不考虑边坡坡度及形态的影响，将坡顶设置为平面；(3)不考虑滑面形态的影响，将滑面设置为水平面，桩后滑坡推力分布形式设为矩形；(4)抗滑桩模型为单排实体桩模型，坡体和抗滑桩的布置具有对称性。

计算模型如图1所示，桩截面尺寸为2m(宽)×3m(高)，桩间距为6m。为了使桩后土拱能较好形成，故取模型边坡后部的计算长度为3倍桩净距，即桩后坡体长12m，桩前坡体长15m，以减少人工边界的影响。边坡模型宽为4倍桩间距即24m，模型上部土体计算深度10m，悬臂段桩长10m，以避免实际工程中悬警段桩前开挖土体清方形成的临空面因受荷段过高导致的桩间土体和桩后土体的坍塌影响模拟计算，下部土体计算深度15m，嵌固段桩长10m。模型内每个单元都是边长为0.5m的正六面体，边坡和桩体模型内共有155134个接触节点，143136个正六面体单元。按弹性本构模型计算实体桩模型部分，以M-C本构模型计算边坡土体部分。模型的计算参数见表1。

表1 边坡主要物理力学参数

图1 边坡数值模拟模型

施加在土体后侧的推力荷载取为400kN/m，按矩形荷载分布施加与模型受荷段土体后侧。计算步骤如下。

(1)通过命令流划分网格并建立模型，将命令流导入FLAC3D进行计算。

(2)模型垂直于x轴的悬臂段桩后坡体后侧界面设置横向位移约束边界，计算模型的初始应力、位移。

(3)先将模型内桩、土体产生的初始位移清零，然后解除悬臂段桩后坡体后侧界面的横向位移约束并在该截面施加矩形均布压应力，进而模拟悬臂式抗滑桩在坡体推力作用下的桩-土相互作用，将坡面与滑面都设置为水平面避免了因其角度改变引起的坡体推力大小改变，通过改变坡体后侧施加的压应力模拟不同体量的滑坡情况。

3 桩后土拱效应模拟

3.1 悬臂段桩后土体正应力云图

桩顶面向下各深度的桩后土体正应力云图如图2所示，从图可以看出桩后一定土体范围内形成了明显的拱形区域，在深度z分别为3、5、7和9m时，桩后土体最大正应力分别为2.76×105、6.0×105、1.02×106、1.54×106Pa，显然，随着抗滑桩后深度增加，最大主应力成逐渐上升的趋势从图中土拱迹线可知，桩后土体深度越深，产生的土拱效应越不明显，且自桩顶面向下拱形区域逐渐缩小。

图2 不同深度的桩后土体应力云图

3.2 悬臂段桩后土体应力矢量图

不同深度水平切面的应力矢量图如图3所示。由图3可知，自桩顶向下不同深度水平切面上桩后土体主应力发生了明显偏转。悬臂段桩后土体水平方向应力逐渐分别以桩间对称线向竖直方向偏转。拱顶点位于桩间对称线上，该点主应力方向由水平向发生90°偏转至沿竖直方向，越靠近桩背侧，主应力又逐渐从拱对称点沿拱迹线由竖直方向偏转到水平方向，所以桩后土拱能将拱后的剩余坡体推力传递至抗滑桩上。应力矢量偏转范围随着深度加深而逐渐缩小，说明土拱效应是随深度加深逐渐减弱的。

图3 不同深度水平切面应力矢量图

3.3 桩后土拱三维形态分析

分析各深度y方向应力沿深度变化曲线，可得到对应深度的y方向应力极大值与极小值点对应坐标，并得到各深度桩间对称线上土拱前、拱轴线及后缘界线如图4所示。

图4 不同深度桩间对称线上土拱界线变化情况

由图4可知，根据数值模拟得到的土拱前后缘界线和理论计算的裂缝位置，土拱厚度随深度加深而逐渐减小，从z=0m至z=2m深度范围内拱的模拟计算和理论计算裂缝距临空面距离基本保持不变，而理论计算的裂缝位置基本位于模拟得到的前后缘居中位置，随着深度加深，土拱厚度逐渐减小，在z=3～7.5m范围内模拟前缘线与理论计算前缘线逐渐接近且差值小于1m，深度z=7.5m以下，模拟土拱界线则逐渐前移接近临空面，在深度z=2～8m以下根据y方向应力所得的土拱前后缘界线重合，此时模拟所得的土拱效应在此深度下不再明显，而基于理论计算得到的裂缝界线也基本不变，此时桩受荷段底部水平面处土拱厚度达到最小值。在z=2～10m深度范围内模拟和理论计算的裂缝界线虽然有一定差距但趋势大致呈随深度逐渐前移，距临空面距离减小的趋势。

基于图4得到的模拟土拱的前后缘界线，提取模型中中间两桩桩后土体不同y坐标在各深度上的y方向应力变化曲线，获得对应前后缘界线y方向应力的等值线点，并根据各等值线点可大致描绘出桩后土拱的三维形态如图5所示。

图5 桩后土拱三维形态图

模型中由y方向应力变化确定两桩间桩后土拱的后缘三维形态，土拱在三维形态上呈上宽下窄，后陡前缓的近楔形体形状，距坡顶深度越深土拱后缘越接近凌空面，土拱最大深度为10m，最小深度为0.5m。越接近桩侧面，土拱后缘线逐渐前移，且变化趋势较桩间对称线处的土拱后缘界线更陡，在深度z=2m附近处桩侧截面的土拱后缘界线前凸，深度再往下土拱后缘界线又逐渐后移直至深度接近受荷段底部时土拱后缘界线才逐渐贴近至临空面。

3.4 影响临界破坏界线变化的因素分析

3.4.1桩间距

在桩宽、土体抗剪强度参数和滑坡推力不变时，设定桩宽为2m，桩间距分别为L1=5m，L2=6m，L3=7m 3种情况，分析这三种情况下拱前土体临界破坏界线沿深度变化的规律。各桩间距情况下的拱前土体临界破坏界线的变化如图6所示。

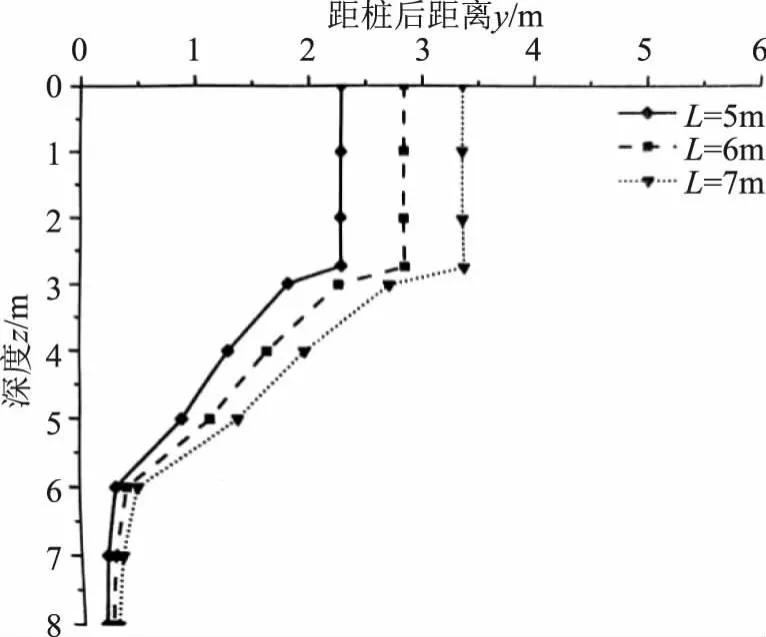
图6 临界破坏界线变化曲线

由图6可知，从地表面到深度2.7m范围内，该阶段各桩间距对应的临界破坏界线距桩背侧大小不发生变化，此时L1、L2、L3的临界破坏线距桩后距离分别为2.2、2.8、3.3m。随着桩间距的增加，临界破坏界线距桩背侧距离明显增大，深度z0以下则呈非线性减小趋势。当深度为6m时，L1、L2、L3的临界破坏线距桩后距离分别为0.25、0.3、0.34m。当桩后土体深度达到8m时，L1、L2、L3的临界破坏线趋于重叠，桩后距离在0.1～0.2m之间。桩间距过大时，在临空面后的区域土体可能破坏的范围更大，安全隐患更大，因此，应按合理桩间距布置抗滑桩。

3.4.2桩宽

设定桩间距L=5m，其他参数不变，只改变桩宽，计算得到不同桩宽(b1=1m，b2=2m，b3=3m)条件下拱前土体临界破坏界线沿深度方向的变化如图7所示。

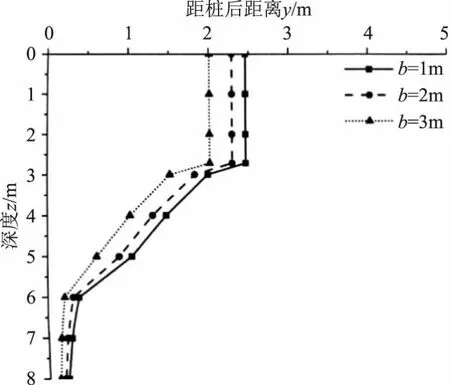
图7 不同桩宽土拱临界破坏界线

由图7可知，在保持桩间距不变，只改变截面宽度时，拱前士体临界破坏界线距桩背侧距离呈随桩截面宽度增加呈非线性减小规律。在z=3m范围内，不同桩宽的抗滑桩临界破坏线基本保持不变，b1、b2、b3的临界破坏界线距桩后距离分别为2、2.4、2.5m。随着深度增加，由于桩间距不变，桩宽增大，而桩间净距随之减小，即拱前土体临界破坏界线距桩背侧距离随桩间净距减小而减小。

4 结语

本文采用有限差分数值模拟软件FLAC3D，研究了抗滑桩桩后土体应力分布规律以及影响因素，得到如下结论。

(1)悬臂式抗滑桩随着桩后土体深度增加，最大主应力也逐渐增大，产生的土拱效应越不明显。最大主应力随深度增加从拱对称点由水平方向偏转到竖直方向，将剩余下滑力传递至抗滑桩。

(2)土拱在三维形态上呈上宽下窄，后陡前缓的近楔形体形状，距坡顶深度越深土拱后缘越接近凌空面。土拱最大深度为10m，最小深度为0.5m，且在深度2m附近处桩侧截面的土拱后缘界线产生明显突变。

(3)由于边坡治理土拱效应影响因素复杂，文章仅采用数值模拟方式进行分析，理论计算模型与实际情况存在偏差，研究结论应结合实际情况确定。