基于启发式算法的重力式挡土墙压力计算及截面优化设计

范晓香

(临沂市水利水电工程建设监理中心，山东 临沂 276000)

自改革开放以来，城镇化进程不断推进，公路、道路、隧道、桥梁等工程不断增多，并且工程地质环境复杂程度也在不断提升，当面临土体结构容易变形，基础稳定性较弱的软土地基时，为了保证工程质量与安全，防止滑坡以及塌方等事故发生，就会利用到挡土墙，利用挡土墙支撑土体，提升土体结构的稳定性与安全性。目前挡土墙已经被得到广泛应用，尤其是重力式挡土墙，重力式挡土墙多用作陡坡路基的路肩墙，由于施工难度较低、工程造价较低以及支撑效果良好，目前在道路工程中广泛使用。重力式挡土墙性能能否得到有效发挥，与其截面设计有直接关系，重力式挡土墙截面优化设计需要结合实际受力情况，因此挡土墙压力计算与截面优化设计是重力式挡土墙设计中重要环节。挡土墙压力计算是一个比较复杂的土力学问题，因此具有较高的难度。国内重力式挡土墙应用起步比较晚，相关计算与设计理论还不够完善，现行的压力计算与截面优化设计方法仍旧沿用普通挡土墙设计方法，并不适用于重力式挡土墙，导致在实际工程中压力计算误差比较大，而且截面优化后的挡土墙抗滑稳定安全系数比较低，无法满足实际工程需求，为此提出基于启发式算法的重力式挡土墙压力计算及截面优化设计。

1 基于启发式算法的重力式挡土墙压力计算及截面优化设计

1.1 重力式挡土墙压力计算

根据重力式挡土墙受力情况，挡土墙压力主要为墙后的土压力，根据挡土墙移动情况以及挡土墙后的土体运动状态，重力式挡土墙压力为静止土压力、被动土压力以及主动土压力之和，在重力式挡土墙处于静止不动的情况下，挡土墙后静止土压力是在挡土墙自重作业下形成的，其计算公式为：

(1)

式中，E—重力式挡土墙静止土压力，kPa；ε—重力式挡土墙后土的重度，kg/m3；h—重力式挡土墙高度，m；k—重力式挡土墙后土的侧土压力系数；ρ—重力式挡土墙后土的有效内摩擦角，(°)。

在静止土压力的作用下，重力式挡土墙会发生位移，此时重力式挡土墙压力转化为主动土和被动土压力，利用朗金理论计算重力式挡土墙主动土压力和被动土压力，其计算公式为：

(2)

式中，Ea—重力式挡土墙主动土压力，kPa；υ—重力式挡土墙内摩擦角，(°)；c—重力式挡土墙后填料的粘聚力，kPa；Eb—重力式挡土墙被动土压力，kPa；μ—重力式挡土墙外摩擦角，(°)。

将以上计算的3种土压力相加，即可计算得出重力式挡土墙压力：

S=E+Ea+Eb

(3)

式中，S—重力式挡土墙压力，kPa。

以此完成重力式挡土墙压力计算。

1.2 截面优化目标函数及约束条件设定

此次将重力式挡土墙截面优化问题转换为一个非线性多参数的目标规划问题，从重力式挡土墙经济性角度出发，以重力式挡土墙截面面积最小为目标，建立优化目标函数，其用公式表示为：

在医学院校的教学中，案例教学效果非常有利于学生的理解与接受[1]。《数据库语言》课程在医学院校中是作为基础课程开设的，修习的都是大学二年级本科生。在此之前他们都在《计算机基础课程》中掌握了EXCEL和网络应用。在常规的《数据库语言》课程体系中，第一堂课内容都是数据库理论和基本概念，对于学生而言，这些枯燥的理论和概念，使得他们由上课起始的兴致勃勃转成听课中的昏昏欲睡，继而失去了对数据库课程的兴趣。结合时代发展和学生今后工作及科研需求、提高学生学习兴趣，是数据库课程教学改革的目的。为此，瞄准关键一课，实施了在第一堂课进行应用案例教学的教学改革。

A=minf(x1，x2，x3，x4，x5)

(4)

式中，A—重力式挡土墙截面优化目标函数；minf—重力式挡土墙最小截面面积，m2；x1—重力式挡土墙的墙面坡比；x2—重力式挡土墙的墙顶宽度，m；x3—重力式挡土墙的上墙墙背坡比；x4—重力式挡土墙的衡重台宽度，m；x5—重力式挡土墙的下墙墙背坡比。

将以上5个参数作为挡土墙截面优化参数，考虑到重力式挡土墙截面优化设计需要满足一定的约束，因此根据挡土墙设计需求，设定约束条件。第一，对重力式挡土墙抗滑稳定性约束，优化后的重力式挡土墙抗滑稳定安全系数要大于容许安全系数，根据上文计算的挡土墙压力，计算出挡土墙抗滑稳定安全系数，计算公式为：

(5)

式中，K—重力式挡土墙抗滑稳定安全系数；G—重力式挡土墙重度，kg/m3；α—重力式挡土墙底部倾角，(°)；β—重力式挡土墙背与土体之间的摩擦角，(°)；γ—重力式挡土墙背倾角，(°)。

根据挡土墙抗滑稳定安全系数大于容许安全系数要求，其墙体抗滑稳定约束条件用公式表示为：

K-[K]≥0

(6)

式中，[K]—重力式挡土墙容许抗滑稳定安全系数。

第二，挡土墙截面优化设计需要满足抗倾覆约束条件，优化后的挡土墙抗倾覆稳定安全系数要大于容许安全系数，挡土墙抗倾覆稳定安全系数计算公式为：

(7)

式中，F—重力式挡土墙抗倾覆稳定安全系数；M—重力式挡土墙的稳定力矩，N·m；A—重力式挡土墙倾覆力矩，N·m。

根据挡土墙抗倾覆稳定安全系数大于容许安全系数要求，其墙体倾覆稳定约束条件用公式表示为：

F-[F]≥0

(8)

式中，[F]—重力式挡土墙容许抗倾覆稳定安全系数。

第三，重力式挡土墙要满足应力约束，其用公式表示为：

(9)

式中，[H]—重力式挡土墙地基容许承载力，kPa；Hmax—重力式挡土墙基底最大应力，kPa；H—重力式挡土墙基底平均应力，kPa。

将以上建立的目标函数和约束条件整合，建立重力式挡土墙截面优化模型，为后续启发式算法对重力式挡土墙截面优化计算奠定基础。

1.3 基于启发式算法的截面优化设计

在上述基础上，利用启发式算法对重力式挡土墙截面优化数学模型求解，优化模型中符合约束条件的截面优化目标函数的可能解有众多个，利用启发式算法对其迭代计算，搜索出可能解中目标函数最优解。将目标函数输入启发式算法中，假设目标函数可能解集为J，每个解为一个个体，利用概率矩阵从目标函数可能解集中采样，以此生成初始种群。在启发式算法迭代计算过程中，个体在搜索空间内对目标进行搜索，个体在搜索过程中会受到启发，概率矩阵通过学习优质个体的分布规律对种群进行更新，更新公式为：

(10)

式中，P(t+1)—更新后的种群，即生成的新的目标函数解集；ς—个体学习率；P(t)—更新前种群；θ—优质个体组成的优质种群；n—迭代次数；In—计算优势种群个体特征的指标函数，即优势种群中某个位置是算法输入的目标函数中最有利得到满意解。

每完成一次迭代计算后，利用适用度函数计算出更新后种群中个体的适应度，适应度是衡量个体与目标之间的距离，适应度值越高，则表示个体与搜索目标之间的距离越近，其对应解与目标越贴近，反之适应度值越小，则个体对应的解与目标越不相符。当算法计算满足迭代要求时，输出种群中适应度值最高的个体，其对应的解为目标函数最优解，即重力式挡土墙截面设计最优方案，根据方案对重力式挡土墙截面参数优化设计，以此完成基于启发式算法的重力式挡土墙压力计算及截面优化设计。

2 对比实验

2.1 实验准备与设计

关于上文设计的基于启发式算法的重力式挡土墙压力计算及截面优化方法，以下将设计一组对比实验，选择两种目前最为常用的方法作为对照对象，为了方便后续实验陈述，以下将两种方法分别用对照组1、对照组2表述，将本文设计方法作为实验组，选择某工程为工程背景，该工程原设计重力式挡土墙高度为3.15m，宽度为2.85m，厚度为0.76m，墙体材料为浆砌石块，挡土墙重度为26.35kN/m3，墙厚填土为不易风化的石块砌体，天然重度为17.56kN/M3，重力式挡土墙基础容许承载力为1500kPa，基底摩擦系数为0.45，按照上述流程对重力式挡土墙压力计算，随机选取一个挡土墙，其压力计算结果如图1所示。

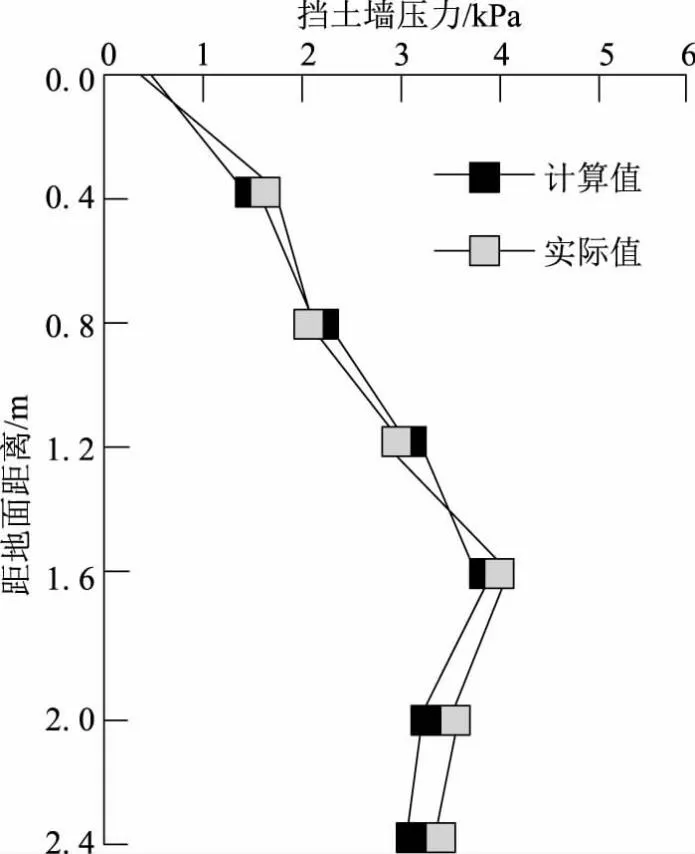
图1 重力式挡土墙压力计算结果

利用启发式算法对挡土墙截面优化目标函数求解，优化后的挡土墙截面面积为56.46m2，上墙墙面坡比为1.26，下墙墙背坡比为1.03，墙顶宽度为2.65m，衡重台宽度为0.86m，偏心距为0.25m，以下对具体优化效果进行对比分析。

2.2 实验结果与讨论

对于重力式挡土墙压力计算精度，选择误差作为指标，将计算值与实际挡土墙压力值作差，求出挡土墙压力计算误差，使用电子表格对实验数据记录，具体数据见表1。

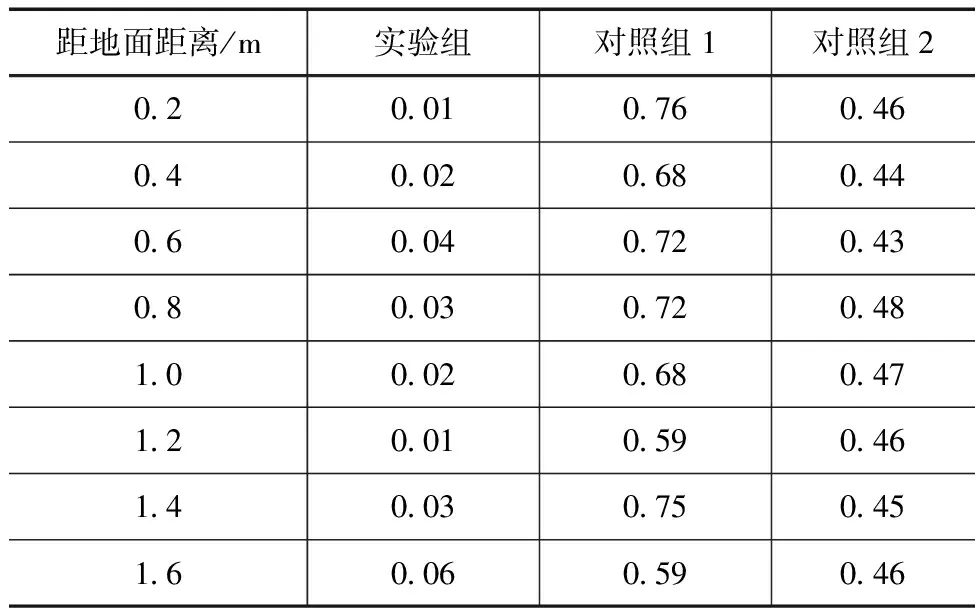
表1 3种方法挡土墙压力计算误差 单位：kPa

由表1知，3种方法在挡土墙压力计算误差方面表现出明显的差异，设计方法平均计算误差为0.02kPa，对照组1对于挡土墙压力计算误差平均值为0.71kPa，对照组2对于挡土墙压力计算误差平均值为0.41kPa，对照组计算误差远远大于实验组，因此证明在挡土墙压力计算精度方面设计方法优于传统方法。对于重力式挡土墙截面优化效果，选择挡土墙抗滑稳定安全系数为指标，抗滑稳定安全系数越高，则表示重力式挡土墙稳定性越好，实验随机选取8个重力式挡土墙，将3种方法优化后挡土墙抗滑稳定安全系数对比，具体数据见表2。

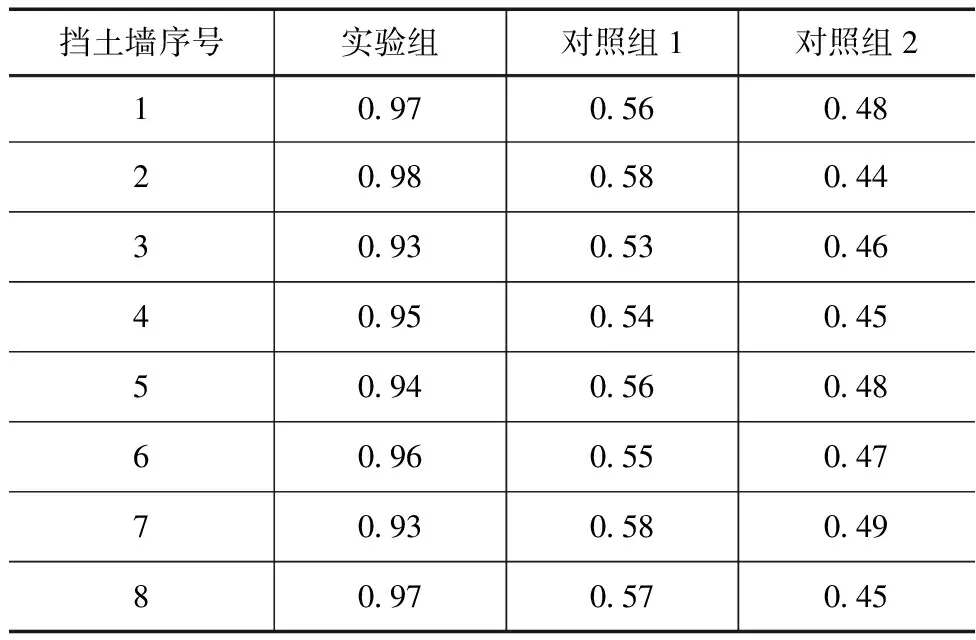
表2 3种方法应用下重力式挡土墙抗滑稳定安全系数

由表2可知，在设计方法应用下挡土墙抗滑稳定安全系数处于较高的水平，平均抗滑稳定安全系数为0.95，可以将其控制在0.9以上，证明优化后重力式挡土墙的抗滑性能显著提升，抗滑稳定性较高。相比之下，设计方法应用下挡土墙抗滑稳定安全系数比对照组1高将近0.4，比对照组高将近0.5，具有良好的优化效果。因此通过以上实验数据和实验结果可以证明，在挡土墙压力计算精度方面以及在挡土墙截面优化效果方面，设计方法均具有明显的优势，相比较两种传统方法更适用于重力式挡土墙压力计算与截面优化设计。

3 结语

重力式挡土墙作为一种重要的基础和围岩支撑和加固组织，对保障周围岩土结构安全起到重要作用，此次针对现行方法的不足和缺陷，结合启发式算法优势，将其应用到重力式挡土墙压力计算与截面优化设计中，提出了一个新思路，有效减小了压力计算误差，提高了挡土墙抗滑稳定性，为重力式挡土墙压力计算及截面优化设计提供了理论支撑，同时也为该方面相关研究提供了参考依据，具有一定的现实意义和理论意义。但是本文研究方法目前尚处于初步探索阶段，尚未在实际中得到大量的实践与应用，在某些方面或许存在不足，今后会在该方面展开深层次探究，促进重力式挡土墙应用广泛推广。