基于头峰的多步分解反应过程热失控特征参数计算方法研究

乔德乾，翁仕春，郭子超，饶国宁

（南京理工大学化学与化工学院， 江苏 南京 210094）

0 引 言

化工生产过程中的热危险性主要表现为反应失控［1］。近年来微通道反应技术得到快速发展，微通道反应器传热效率高、持料量微小的特点极大地降低了反应热失控的风险，在严重依赖危险化学品工艺过程的精细化工领域具有无可比拟的优势［2-3］。但是在涉及危险化学品，尤其是含能材料时，微通道反应器中反应物、中间体、产物本身的热稳定性分析依然是反应安全风险评估中必不可少的环节。《精细化工反应安全风险评估规范》（GB/T 42300-2022）［4］提出，在反应失控可能性评估和反应工艺危险度评估中，采用绝热情况下最大反应速率到达时间（TMRad）以及TMRad等于24 h 的引发温度TD24等热失控特征参数，作为评估危险等级、确定工艺温度的重要因素，其主要通过热分析设备如加速度绝热量热仪、差示扫描量热仪（differential scanning calorimeter， DSC）分析计算获得。

目前计算TMRad和TD24的传统方法主要有单步N级法和基于模型的数值计算法［5］。传统的单步N级法是基于单步N级反应模型进行动力学分析计算，缺点是不能描述复杂的分解反应，对于呈现出自催化特性和多步分解反应的物质，TMRad和TD24的计算结果会产生较大的偏差［5-6］。数值计算法是基于完整的反应模型进行动力学计算和TMRad求取［6］，解决了传统算法只适用于N级模型的问题，且计算精度高。但由于多步分解模型的不确定性和难以验证，使得准确获取每一步反应的分解动力学信息比较困难［7-9］，不仅对研究人员的专业能力要求较高，且需要耗费大量的时间精力去验证模型的准确性［10］。

含能材料的分解过程通常比较复杂，其DSC 热流曲线表现为复杂的多步过程。为此有学者开始研究基于分解放热头峰的计算方法。Zhu 等［11］利用DSC 对3，4-二硝基呋咱基氧化呋咱（DNTF）反应液热解特性进行了研究，测得其分解过程为多步分解过程，但并没有对头峰进行分峰处理，直接选取了头峰的部分数据进行动力学分析，并进行了热分解特征参数计算。该方法仅对头峰的部分数据进行动力学分析，偏差较大，也没有对其有效性进行验证。朱益［5］发现当多步分解过程的第一步遵循N级动力学时，采用外推法对第一段放热计算TMRad和TD24，结果与理论值较为接近，但未作更深入的分析与研究。

目前尚缺乏高效、精确的含能材料热分解特征参数计算方法。为进一步简化多步分解反应的热失控特征参数计算过程，本研究提出基于头峰（即多峰曲线分峰后的第一个峰）的多步分解反应热失控特征参数的计算方法。利用穷举法进行数值模拟生成多步分解反应DSC 放热速率曲线，采用头峰方法计算获取TMRad和TD24，并与基于总反应模型的数值计算法结果（以下称理论值）进行比较，验证该方法可行性。随后对1，8-二硝基蒽醌、改性硝基胍（M-NQ）、1，5-二硝基蒽醌和3，4-二硝基呋咱基氧化呋咱（DNTF）4 种含能材料的文献实验数据进行分析计算，与已知基于总反应机理模型的计算结果比较，分析该方法的偏差。

1 基本原理与方法

1.1 基本原理

在理想绝热条件下，分解反应放出的所有热量均用来加热物料本身，分解物料的温度会上升。假设物料的比热容是定值，则转化率α与反应能量的关系如式（1）［12］：

式 中，C为t时 刻 反 应 物 的 浓 度，mol·L-1；C0为 初 始 时刻反应物的浓度，mol·L-1；ΔHt为0 至t时间区间内的放热量，J；ΔHtotal为总放热量，J；Ton为起始分解温度，℃；Tf为绝热分解的终点温度，℃；ΔTad为绝热温升，℃。

对式（1）进行微分，可以得到温升速率与转化速率之间的关系：

对式（2）进行积分，可以得到TMRad的计算公式［8］：

式中，t0为起始温度T0处所对应的时间，s；tm为最大温升速率处对应的时间，s；Tm为最大温升速率对应的温度，℃。

含能材料的分解过程往往比较复杂，表现出多步分解特征，其DSC 热流曲线会呈现出多个放热峰［13］：绝热条件下多步分解过程的温度升高速率为［7］

式中，n为反应步数；αi为第i步的转化率；ΔTad，i为第i步绝热温升，℃；Ai为第i步的指前因子，s-1；Ei为第i步的活化能，kJ·mol-1；R=8.314 J·K-1·mol-1；f（αi）为第i步的反应机理函数。

将式（4）代入式（3），可以得到多步分解反应的TMRad计算，如式（5）：

从式（5）可以看出，TMRad的量纲为时间，单位为秒。常见的热失控特征参数为TD24，其量纲为温度，单位为摄氏度。通常来说，TD24的值比由热分析技术测试得到的起始放热温度要低很多。由此可以推断，即使含能材料的分解过程表现出多步特征，但是当温度低于起始放热温度时，其放热速率由第一步放热速率决定［7］。以DSC 为例，含能材料的DSC 热流曲线可能呈现出多个放热峰，但是当温度低于起始放热温度时，其放热速率由第一个放热峰（即头峰）对应的分解过程决定。因此，只要能获得头峰的热分解动力学模型和参数，即可计算TD24。

对于含能材料而言，其分解热通常较大。这意味着在绝热分解过程中，当温度高于起始放热温度后，物料的温度将迅速达到最大放热速率对应的温度Tm。由此可以推断，基于头峰计算得到的TD24c与实际值TD24E偏差会很小，见式（6）：

换言之，基于头峰计算得到的最大反应速率处的温度Tmc与实际值TmE的时间差，即tmc至tmE相比24 h 可忽略不计，如图1 所示。

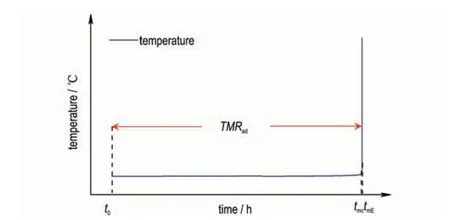
图1 TMRad示意图Fig.1 Diagram of TMRad

基于此原理，本研究提出基于头峰的热失控特征参数计算方法。该法的主要流程（见图2）为：（1）通过数学分峰法获得头峰的热流曲线；（2）判定头峰的分解模型；（3）拟合动力学参数。由于头峰的热分解动力学模型及参数更容易获得和验证，以此方法预测绝热过程将更加简便、高效。

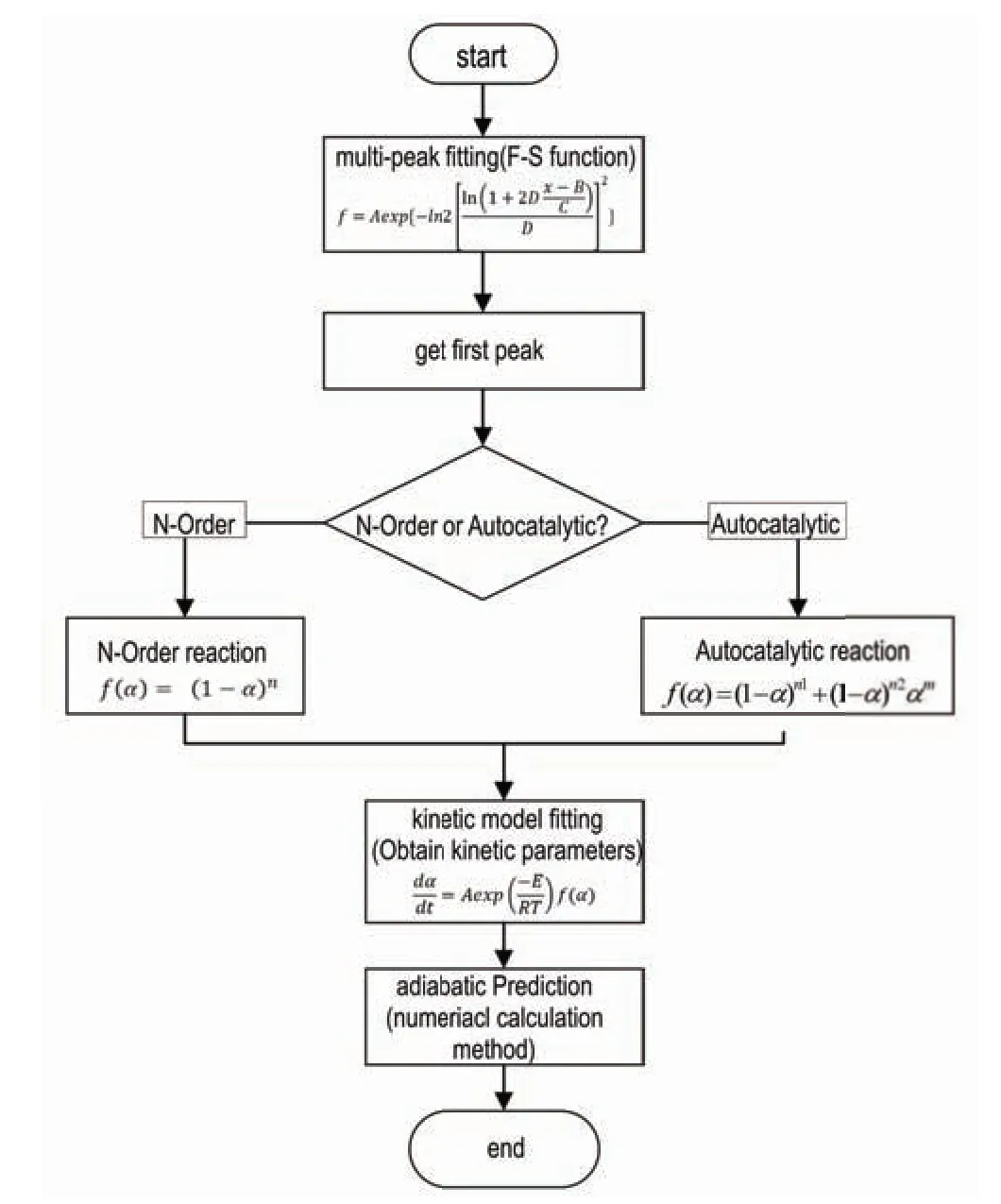
图2 基于头峰的热失控特征参数计算流程图Fig.2 Flowchart illustrating the computation of thermal runaway parameter based on the first peak

1.2 数学分峰获取头峰热流曲线

连续分解反应的DSC 动态曲线呈现为多个峰，可采用数学分峰的方式将复杂的多步反应分离为单个反应，并对单个反应进行分析［14］。不论分解反应是N级还是自催化反应，Fraser-Suzuki 函数（F-S 函数）都能良好拟合理想动力学模型的曲线［7，14-17］，如式（7）。使用2 个F-S 函数对两步分解的模拟热流曲线进行非线性拟合（动力学参数为A1=e44.9s-1，E1=205.5 kJ·mol-1，n1=3.0；A2=e30s-1，E2=160 kJ·mol-1，n2=1.0；Q1∶Q2=7∶3），拟合相关系数R2=0.999，如图3a。通过拟合结果中第一个F-S 函数获得头峰曲线，如图3b。

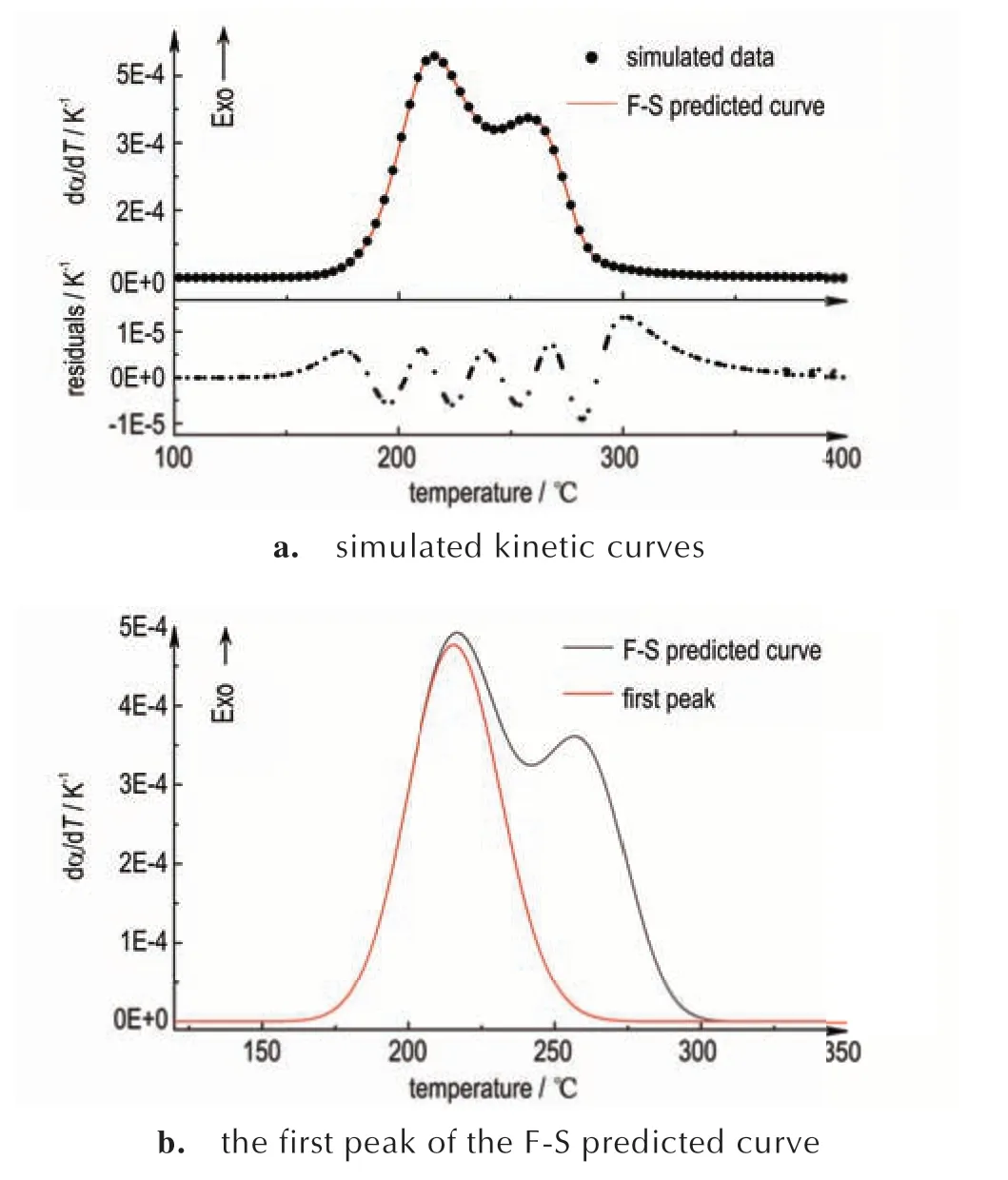
图3 F-S 函数多峰拟合及获取头峰Fig.3 Multi-peak fitting using the F-S function and obtaining the first peak

式 中，A为 振 幅；B为 峰 位 置；C为 半 峰 宽；D为 不 对称度。

1.3 头峰曲线动力学拟合

若物质分解为N级反应，其机理函数可以表示为f(α) =(1 -α)n；若 为 自 催 化 反 应，假 设 其 遵 循Benito-Perez 模型［5］（BP 模型），其机理函数为f(α) =(1 -α)n1+(1 -α)n2αm，该模型在描述自催化过程有较好的通用性［18-19］。

根据数学分峰获得头峰曲线后，可根据DSC 等温或中断回扫实验判断其是否为自催化反应［12，20-23］。然后利用N级模型或自催化模型对头峰进行拟合，得到第一步反应的动力学参数。拟合过程基于最小二乘法Levenberg-Marquardt 算 法［24］，用 于 拟 合 的 模 型 公 式如式（8）所示。

2 数值模拟验证

采用穷举法比较本研究方法与模型计算法得到的TD24之间的偏差，以此验证本方法的有效性。为此，假定多步连续分解反应动力学模型和模型参数（指前因子、活化能、反应级数）已知，基于Python 程序，通过数值模拟生成多步分解反应的DSC 动态曲线。以两步N级连续反应A→B→C 为例，其分解反应动力学模型如式（9）所示。

式中，α和γ分别为反应物A 的转化率和产物B 的得率。模拟生成的曲线见图4（动力学参数为A1=e44.9s-1，E1=205.5 kJ·mol-1，n1=3.0；A2=e30s-1，E2=160 kJ·mol-1，n2=1.0；Q1∶Q2=7∶3）。

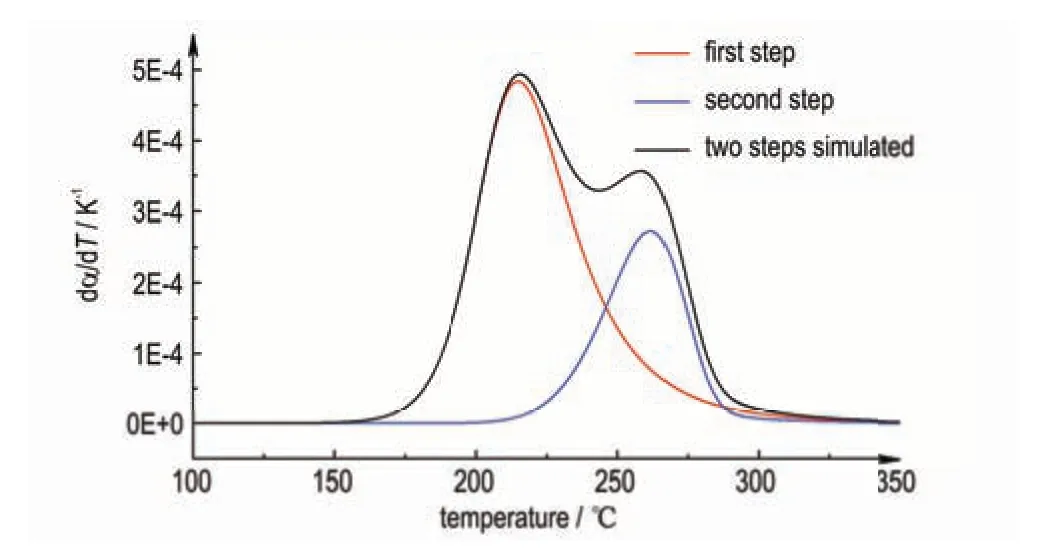
图4 模拟两步N 级连续分解反应DSC 曲线Fig.4 Simulation of DSC curves for a two-step N-order continuous decomposition reaction

2.1 动力学参数设置

根据含能物质的分解动力学参数统计结果［8］，其范 围 是：指 前 因 子A为 e4～e46s-1，活 化 能E为50～250 kJ·mol-1，反应级数n为0.1～3.0。本研究以两步和三步连续反应为验证模型，利用穷举法，对所有动力学参数进行等差排列，生成大量得动力学参数组合。其中两步连续反应类型由N级、自催化反应组合为4 种。三步反应模型由于模型数量及计算量限制，第一步反应由N级、自催化反应组合，共生成81000 个反应模型组合。两步连续反应和三步连续反应得动力学参数设置情况见表1、表2。

表1 两步连续分解反应数值模拟参数Table 1 Parameters for numerical simulation of a two-step continuous decomposition reaction

表2 三步连续分解反应数值模拟参数Table 2 Parameters for numerical simulation of a three-step continuous decomposition reaction

模拟计算过程中会出现两种非理想情况。第一种非理想情况是模拟计算得到多个放热峰相互独立，此时仅需对第一步反应分析即可。第二种非理想情况是计算结果不收敛。去除这两种非理想情况，两步连续反应和三步连续反应得有效模拟样例分别为5853 个和2630 个。运用本文提出的方法对多步分解反应DSC 模拟曲线进行绝热预测，计算其TD24值，并与模型计算法得到TD24［5］进行比较。

在数值模拟过程中由于穷举产生大量的模拟样例，因此将头峰方法实现Python 程序化，以便对所有模拟样例进行批量处理。其次是使用F-S 函数多峰拟合的精度对计算结果影响大，需尽可能提高拟合精度。本研究得拟合相关系数R2均不低于0.999。

2.2 数值模拟结果

2.2.1 两步连续反应

基于头峰方法和模型计算法得到的TD24偏差统计见图5，横轴为偏差大小，纵轴为计算偏差出现的频次。偏差为正说明头峰方法的结果高于模型计算法，其结果冒险。偏差为负说明头峰方法的结果低于模型计算法，其结果保守。

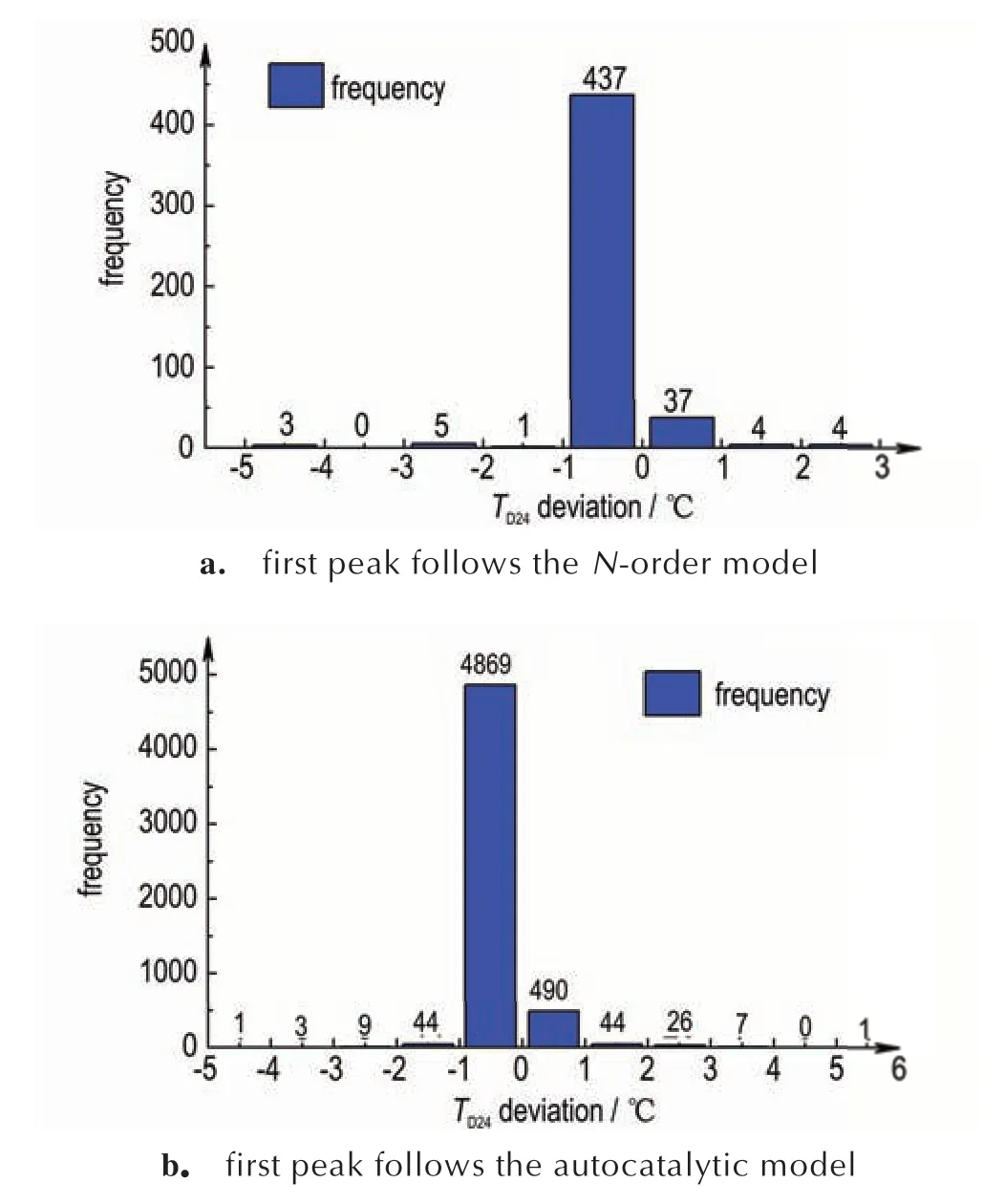
图5 两步反应TD24偏差统计分析Fig.5 Frequency of TD24 deviation for the two-step reactions

图5a 显示当头峰是N级反应时，474 个模拟样例（占96.54%）的TD24偏差绝对值小于1 ℃，TD24的最大偏差绝对值为4.61 ℃，所有模拟样例偏差百分比均未超过5%。当头峰是自催化反应时（见图5b），5179 个模拟样例（占96.53%）TD24偏差绝对值小于1 ℃。4926 个模拟样例（占91.81%）的偏差为负，结果偏保守。头峰为自催化反应时的TD24最大偏差温度为6.41 ℃，此时偏差百分比仅为2.88%。以上结果表明对于两步连续分解反应，无论头峰是N级反应还是自催化反应，头峰方法都能够准确可靠地评估TD24。

2.2.2 三步连续反应

三步连续反应数值模拟计算TD24的偏差统计分析见图6。当头峰为N级模型时（见图6a），153 个模拟样例（占87.93%）的TD24偏差绝对值小于1 ℃，167 个模拟样例（占95.98%）的TD24计算结果更为保守。TD24的最大偏差温度为5.39 ℃，最大差百分比为6.9%。当头峰为自催化反应时（见图6b），2211 个模拟样例（占90.02%）的TD24偏差绝对值小于1 ℃，2301 个模拟样例（占93.69%）更为保守，TD24的最大偏差温度为5.17 ℃，最大偏差百分比为5.89%，偏差均在可接受范围内。这表明头峰方法在三步连续反应情况下也能较为准确可靠地评估TD24。

图6 三步反应TD24偏差统计分析Fig.6 Frequency of TD24 deviation for the three-step reactions

对比两步与三步连续反应的TD24偏差统计可以发现，不论是两步还是三步连续反应，运用头峰方法计算TD24，偏差范围均较小，验证了本研究提出方法的在计算热分解特征参数时的有效性。另外，统计结果显示绝大部分情况下较为保守，在热危险性评估中具有实践意义。

3 实验应用

3.1 实验应用对象

为进一步说明本研究提出方法的实用性，本研究选取4 种含能材料作为实验应用对象：1，5-二硝基蒽醌、3，4-二硝基呋咱基氧化呋咱（DNTF）、1，8-二硝基蒽醌和改性硝基胍（M-NQ）。根据文献资料［8-9，25］，1，8-二硝基蒽醌和M-NQ 呈现两步连续分解过程，1，5-二硝基蒽醌呈现出三步连续分解过程，DNTF呈现出四步分解过程。其中，1，8-二硝基蒽醌和M-NQ 的头峰为自催化反应模型，剩余两个对象的头峰遵循N级动力学模型［8-9，25］。

3.2 动力学参数分析

4 个样品的DSC 热流曲线均从文献中获取。首先对4 个样品的DSC 热流曲线进行分峰处理，获得独立的头峰。以升温速率1 K·min-1曲线为例，四个样品的数学分峰效果见图7，拟合相关系数R2均大于0.998，表明分峰效果良好［15］。拟合自催化模型时采用广义自催化模型［26］，其反应速率方程可表示为式（10）。

图7 F-S 函数多峰拟合效果Fig.7 Results of multi-peak fitting with F-S function

式中，Ez为引发反应和自催化反应的活化能之差，kJ·mol-1；Z0为引发反应和自催化反应的指前因子之商；n1，n2分别为引发反应和自催化反应的反应级数。

对获得的头峰热流曲线进行动力学拟合，获得头峰的分解动力学参数。表3 中对比了通过本研究方法获得的头峰动力学参数与理论值。可以看出，理论值与本研究方法获得的头峰动力学参数值接近，表明数学分峰处理对头峰的动力学参数拟合影响较小。

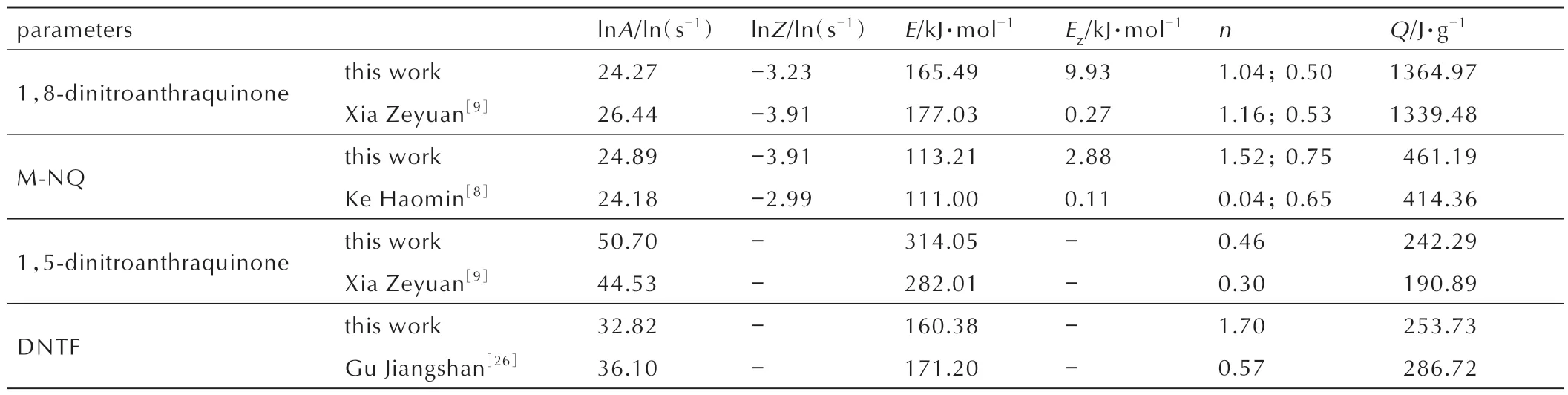
表3 拟合头峰动力学参数与相关文献结果对比Table 3 Kinetic parameters of this study and other relevant investigations

3.3 TMRad计算

在头峰动力学参数的基础上预测TMRad，与基于模型拟合法获得TMRad理论值比较［8-9，26］，结果见图8。

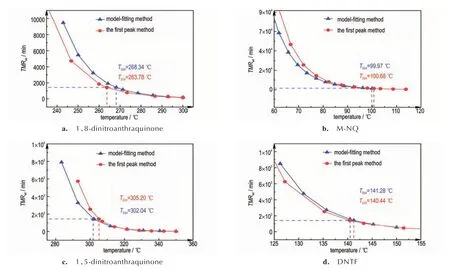
图8 头峰法计算的TMRad与基于模型拟合法获得总反应机理获得的TMRad理论值比较Fig.8 Comparison of the TMRad calculated using the first-peak method with its corresponding theoretical true value

从图8 可以看出，利用头峰方法计算的TMRad与理论值值偏差均较小。头峰方法预测1，8-二硝基蒽醌TD24与理论值的偏差为-4.55 ℃，偏差百分比为1.70%（图8a）；，M-NQ 的偏差为0.71 ℃，偏差百分比为0.71%（图8b）。结果均较为准确。

1，5-二硝基蒽醌与DNTF 的分解过程分别为三步和四步反应。基于头峰法计算的1，5-二硝基蒽醌的TD24与理论值的偏差为3.16 ℃，偏差百分比为1.05%（图8c），略为冒险。 DNTF 的计算结果与理论值的偏差为0.84 ℃，偏差百分比为0.60%（图8d）。由上述分析可知，基于头峰动力学参数对多步分解反应进行绝热预测的方法具有可靠性，预测结果均较为准确。

3.4 偏差原因分析

当头峰为最大放热速率过程时，即DSC 曲线上第一个峰为最高峰，第一步反应到达最大反应速率时的温度Tm与总反应一致，可看作积分范围T0～Tm不变。将头峰方法计算的结果表达为TMR´ad和TD24´，模型计算法的计算结果表达为TMRad和TD24。在T0～Tm段TMR´ad与TMRad关系如式（11），可以推出TD24´＞TD24，此时理论上略为冒险。

当头峰非最大放热速率过程时，即总反应的温度Tm与后续某步反应一致，积分范围T0～Tm大于第一步反 应 积 分 范 围T0～T´m。在T0～T´m段 以 头 峰 计 算 的TMR´ad与总反应理论值TMRad关系如式（12）：

在T´m～Tm段，则有式（13）：

所以头峰非最大放热过程时，头峰方法计算的TMR´ad与理论值TMRad的大小关系无法确定。但是由于其时间长度偏差相比24 小时而言可以忽略，所以依然可以使用头峰方法来进行绝热预测，且可以推广到更多步骤的绝热预测中。而在多步反应过程不耦合的情况下，可以看作在两个独立的温度反应内分解，从防止二次分解反应的角度，此时应当以低温下的反应，即头峰反应来进行绝热预测，评估其危险性，因此本方法仍适用。

由上述分析可知，无论多步分解反应DSC 曲线是否耦合，均可基于头峰进行绝热预测，偏差均较小。若耦合时头峰为最大放热速率过程，以头峰进行绝热预测的结果略为冒险；若头峰非最大放热速率过程，以头峰进行绝热预测结果可能保守也可能冒险。

4 结 论

本研究提出了基于头峰的多步分解反应过程热失控特征参数计算方法。并采用数模模拟的方法验证该方法的有效性，通过穷举法得到了两步连续和三步连续反应的TD24。与模型计算法的结果相比，TD24的最大偏差百分比分别为2.88%和6.9%，最大绝对偏差为6.41 ℃，从而验证了本研究提出方法的在计算热分解特征参数时的有效性。相比模型计算法，该方法计算过程仅需基于第一步反应机理，避免了多步模型拟合的不确定性，简化了计算过程，节约实验资源，且结果可靠性高。

另外，本研究将该方法应用于1，8-二硝基蒽醌、M-NQ、1，5-二硝基蒽醌和DNTF 四种含能材料的TD24计算，与模型计算法得到的TD24相比，偏差百分比的绝对值均小于2%，进一步证明了本研究提出的TD24计算方法的有效性。