综合考虑材料热各向异性与多种传热方式的磁性元件热阻网络精准模型
郭 轩 肖云昊 李 驰 郑泽东
综合考虑材料热各向异性与多种传热方式的磁性元件热阻网络精准模型
郭 轩 肖云昊 李 驰 郑泽东
(电力系统及大型发电设备安全控制与仿真国家重点实验室(清华大学) 北京 100084)
磁性元件正在向高频化、小型化、高功率密度的方向发展,随着功率密度的提高,散热已成为影响器件可靠运行的关键因素,因此对磁性元件的热分析提出更高的要求。传统的热分析模型存在运算时间长、传热方式单一等问题,该文引入已有研究中提出的三轴九热阻网络模型,在此基础上添加热对流与热辐射两种传热方式,综合考虑材料热各向异性与热传导、热对流、热辐射。并通过精细划分元件温度计算子区域、实际器件损耗场分析、热电耦合迭代提高模型的计算精度,提出一种更加完善的三轴十五热阻网络模型,基于该模型对实际磁性器件建模,验证了该模型的准确性,并于最后提出一种通用的针对EE、EI、UU等典型磁心构成的磁性元件的热阻网络建模方法。
磁性元件 材料热各向异性 多种传热方式 实际损耗分布 集总参数热阻网络
0 引言
磁性元件在隔离电力电子变换器中扮演着重要的角色[1],变换器在电动汽车及用户储能领域的蓬勃发展正在催生本行业对器件小型化的需求。同时我国电力电子技术在广泛场景的深度应用对器件性能指标与可靠性提出了严苛要求,特别是近年来,纳米晶铁氧体等磁性材料的使用及以SiC和GaN为代表的第三代宽禁带半导体技术的成熟使用使得电力电子变换器的高频化成为必然趋势,变换器的优化设计变得越来越重要[2-4]。作为核心组件,磁性元件的功率密度对电力电子变换器的性能参数有着重要的影响[5],目前许多研究正致力于提升功率密度。
散热设计是磁性元件优化设计中的一个关键步骤,元件内部的温升通常会限制元件的体积[6],散热性能的优劣将直接影响元件的工作性能。然而,磁性元件功率密度的提升使其散热更加困难,使元件的散热管理面临更严峻的考验。为了满足变换器优化设计的要求,保证电力设备稳定可靠运行,科学有效的热性能分析、完善的热力学建模是变换器散热设计中不可或缺的步骤。
目前的主流热分析方法有集总参数建模分析和有限元分析两类。文献[7-8]采用流体相似理论和三维有限元法计算了具有轴径向通风系统的大中型异步电动机定子三维温度场。文献[9]通过电磁-热-结构多物理场仿真实现了铁心电抗器的温度场计算。文献[10]基于有限元计算方法,采用多物理场耦合方法计算对流传热系数,实现了变压器温升的计算和绕组热点预测。文献[11]利用有限元法分析了电机匝间短路故障前后的温度分布。总体来看,有限元分析方法具有较高的精度,但计算复杂度高、耗时长。而磁性元件散热设计的优化往往需要数万次迭代,有限元法较大的时间开销往往难以满足磁性元件优化设计的时间需求。
针对集总参数的热力学分析,文献[12]利用热阻等效网络对75 kV·A三电平背靠背变流器的散热系统进行分析,但仅考虑了热传导一种散热方式。文献[13]建立38节点的永磁同步电机热网络模型,真实反映了电机各部件的温升,并通过与有限元分析结果对比验证了模型的正确性。文献[14]提出了基于等效热网络法的定频双转子发电机热分析,通过建立定频双转子发电机的热网络模型得出电机各部分的稳态温升,并通过实验进行了验证。文献[15]考虑热对流与热传导两种传热方式,通过等效热网络法对电动汽车采用的轮毂电机额定工况下的温度场进行了分析。文献[13-15]都未考虑辐射散热对结果的影响。文献[16]在热平衡原理和热电类比理论基础上,提出功率器件集总参数热路模型,但没有考虑热各向异性对热分析结果的影响。文献[17]对166 kW/20 kHz中频变压器进行了热分析建模,但仅考虑了损耗在磁心均匀分布的情况。文献[18]对中频变压器进行了热分析建模,考虑了热传导、热对流和热辐射,但也仅考虑了损耗在磁心均匀分布的情况。
高功率密度磁性元件往往伴随水冷、风冷等多种散热结构的布置,具有热对流、热辐射、热传导多种散热形式。此外,应用于高频磁性元件的磁心(如非晶、纳米晶等)及绕组(如利兹线)材料多为热各向异性,且实际工作时损耗密度并非处处相等。目前的研究还没有全面考虑实际情况,所提热阻网络针对特定的样机结构,不具有通用性。
本文以EE型高频电感为例,引入了已有研究中的三轴九热阻网络的集总参数热等效网络建模方法,综合考虑热对流、热辐射及热传导三种热效应对器件热力学分析的影响,并将各向异性材料纳入模型。此外,借助该模型对磁性元件内部产热加以考虑,根据实际磁心损耗分布模型,实现了较为完备且具有通用性的针对使用EE、EI、UU等典型磁心设计的磁性元件的热阻网络模型,在保证热力学分析精度的同时具有高效的计算速度,实现了精度高、速度快的集总参数热力学分析,并有望推广为更加普适性的热分析方法。
首先,本文介绍了已有的热阻网络,并通过考虑热各向异性等多方面因素,以EE型电感为例推导得到了整体热阻网络运算模型;其次,通过实验对热阻网络模型进行验证;然后,基于本文提出的综合性热阻网络模型,针对一些典型磁心构成的磁性元件总结了通用性的热建模方法;最后,根据实验与理论结果得出结论,并对未来的工作进行展望。
1 综合集总参数热阻网络建模
1.1 长方体器件三轴九热阻网络
文献[19]综合考虑热传导和器件内部产热,提出了在笛卡尔坐标系下具有内热产生和材料热各向异性的一般长方体单元的集总网络等效——三轴九热阻网络,长方体元件的通用等效热网络如图1所示。R(=,,;=1, 2, 3)为长方体元件中对应方向上的传导热阻,计算公式如式(1)、式(2)所示;T(=,,;=1, 2)为长方体元件与对应方向所垂直平面的温度;为长方体元件内部平均温度。
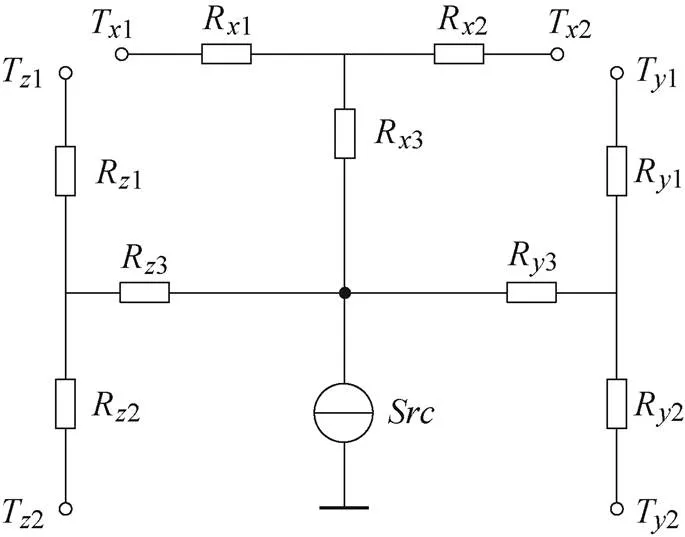
图1 长方体元件的通用等效热网络
三轴九热阻网络中各热阻[19]分别为
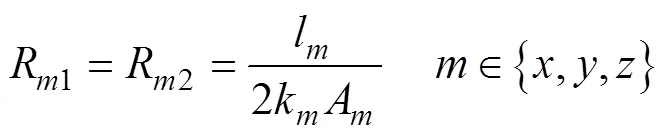

式中,l为长方体对应方向上的长度;k为对应方向上材料的热导率;A为长方体对应方向上的截 面积。
1.2 考虑多种传热方式的长方体元件热阻网络模型
实际应用中,高频磁性元件一般不存在浸没式液冷问题,大多数情况为某一表面置于散热器上。在三轴九热阻模型的基础上,考虑空气对流与磁心表面热辐射对热分析结果的影响,本文在三轴九热阻网络中添加了对流热阻和辐射热阻,假设长方体块置于无限大空气域,中心位于笛卡尔坐标系的原点,三组对立面分别垂直于、、轴,提出了更加完善的三轴十五热阻网络如图2所示。
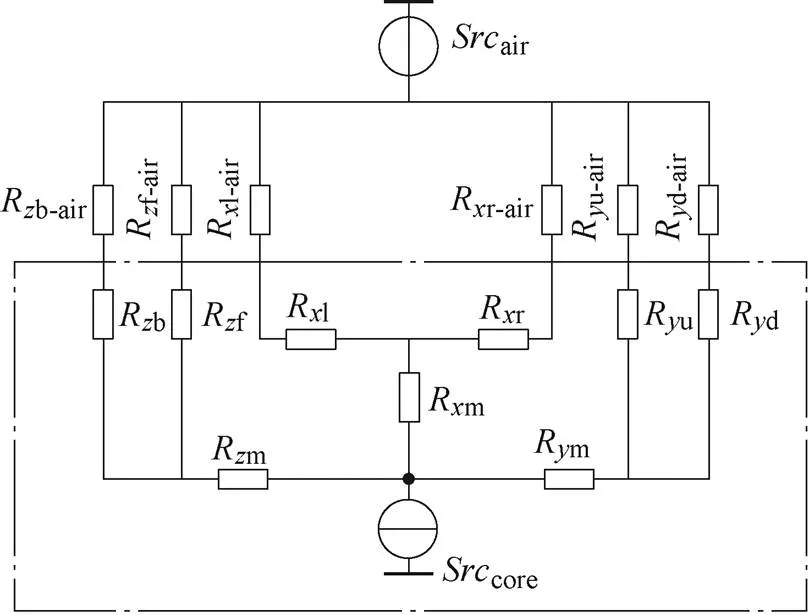
图2 考虑热对流、热辐射的等效热阻网络
图2中,点画线框内区域为三轴九热阻网络,热阻物理含义与图1相对应。点画线框外区域的热阻分别表示长方体元件各表面与空气间的热阻。air为环境温度,cor为内部热源,Rr-air为正方向表面与空气间的热阻,由对流热阻和辐射热组并联等效得到。
传导热阻可以通过式(1)、式(2)计算得到,对流热阻conv与辐射热阻thr计算公式分别为
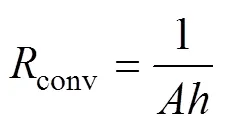

式中,为与空气接触的表面积;s、air分别为截面平均温度和环境温度;为对流传热系数,有三个不同的计算公式,分别对应于顶、侧及底面三个方向,依次表示为式(5)~式(7),其中,air为空气热导率,为特征长度。对于顶面和底面,为表面面积和周长的比值;对于侧面,为表面的高度[18]。瑞利数ray为流体力学中与浮力驱动对流相关的无量纲数,为普朗特数;为玻耳兹曼常数;为辐射系数。



式(3)、式(4)表明,对流热阻和辐射热阻均和温度有关,由于计算前元件温度分布未知,故需要迭代计算。
1.3 考虑热各向异性与多种传热方式的热阻网络理论模型区域化建模方法
实际应用中,在损耗、散热等多种因素的制约下,磁性元件往往没有和长方体一样规则的形状,本文针对EE型、EI型磁心构建了通用性的理论体系。为了验证所提解析模型的准确性,绕制了如图3所示150mH电感实物。电感为EE型,采用两块E型铁氧体磁心,型号为E80/38/20。绕组采用0.1 mm× 1 500 Litz线,均匀绕制三层,总匝数为27。

图3 150 mH电感实物
本文以绕制电感为例,通过区域化的热分析方法,将器件分割为多个具有规则形状的区域,分别通过长方体元件热阻网络模型建模,最后根据磁性元件实际形状连接各区域热阻网络,构建出磁性元件的整体精细热阻网络模型。
1.3.1 磁心处理
根据图4所示的磁心分块示意图将EE型电感的磁心划分为10个长方体块,对每一个子区域分别进行热阻网络建模。为了保证模型的运算速度,磁性元件的区域划分数量不能无限增长,故可能会出现一个或多个区域某一表面同时接触多个区域的情况,以区域1为例,磁心区域划分方案如图5所示。
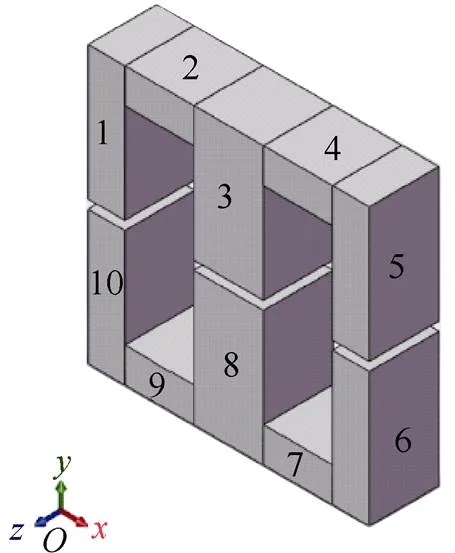
图4 磁心区域划分方案
图5中,1为区域1与区域2接触的面积,2为区域1与右侧空气块接触的面积。此时,子区域1的表面接触多种介质的热等效网络如图6所示。
r1、r2分别为区域1与区域2连接时的传导热阻和区域1与右侧空气块连接时的传导热阻,由式(1)计算得到。r1、r2分别为磁心区域1与磁心区域2接触表面的平均温度和磁心区域1与空气块1接触表面的平均温度。由于本文所用电感磁心材料为铁氧体,不需要考虑磁心材料热各向异性的问题,若磁心材料选择纳米晶则需要考虑热各向异性的问题。
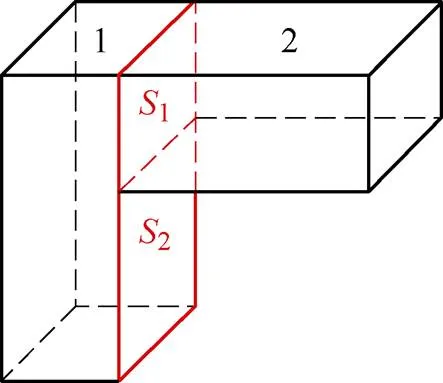
图5 局部磁心框图

图6 表面接触多种介质的热等效网络
1.3.2 气隙处理
为了防止磁饱和现象发生,设计磁性元件时会预留气隙,需要考虑气隙的存在对热分析的影响。本文所使用磁性元件的气隙为弱导磁固体材料填充,可以将气隙部分视作与磁心热导率不同的无内部产热子区域,利用如图7所示的内部无热源的三轴九热阻网络建模。
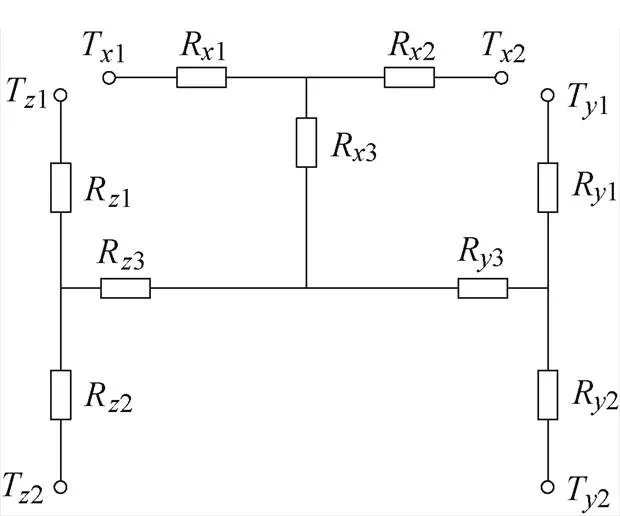
图7 内部无热源的三轴九热阻网络
1.3.3 绕组处理
按磁心中柱侧面的方向将绕组拆分为前、后、左、右四个子区域,各子区域分别使用图1的长方体热阻网络建模,同时考虑热传导、热对流和热辐射三种传热方式。
各绕组子区域与磁心中柱之间的传热方式为热传导;绕组外侧与空气接触部分传热方式为热对流,通过对流热阻连接至环境温度。由于电感使用利兹线绕制,区域内部存在空气间隙,不能使用纯铜材料的热导率描述内部的热扩散方程。此外,利兹线绕组不同方向上的热导率不同,需要考虑绕组区域热导率各向异性的问题。利用文献[20]中的两步均匀化圆柱形导体等效热导率的计算方法和并联等效热阻网络法对绕组各区域在直角坐标系下的等效热导率进行计算。定义变量ii、ci、c分别为空气、导线中绝缘材料、铜的热导率,ii、ci、c分别为空气、导线绝缘材料、铜的体积占比。绕组区域中除铜以外材料的等效热导率a为

根据绕组的对称性,前、后部分绕组热导率相等,左、右部分绕组热导率相等。对于前、后部分绕组,在图4坐标系下,热导率分别为
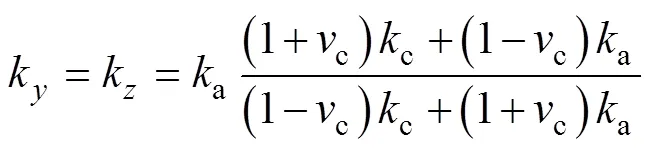
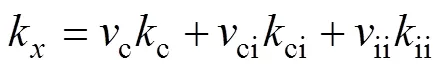
对于左、右部分绕组,在图4坐标系下,热导率分别为
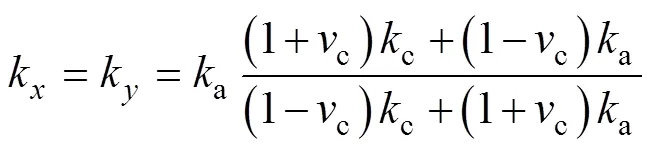
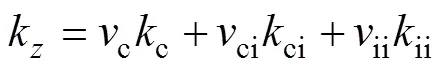
根据实际绕组所用材料,取c=401 W/(m·K),ci=0.2 W/(m·K),ii=0.024 4 W/(m·K)。计算得到绕组各区域热导率,前后部分各向热导率(,,)= (157.556 1, 0.343 5, 0.343 5) W/(m·K),左、右部分各向热导率(,,)=(0.343 5, 0.343 5, 157.556 1) W/(m·K)。
以前端部分绕组为例说明绕组区域热阻网络与周围网络的连接方式。绕组外部包裹聚酰亚胺薄膜,轴方向内侧表面与磁心间的绝缘通过聚酰亚胺薄膜实现。由于聚酰亚胺薄膜热量传递主要为厚度方向且不存在内部产热,仅考虑其厚度方向上的传导热阻,计算方式为
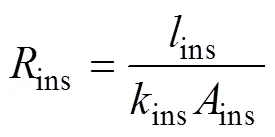
式中,ins、ins、ins分别为对应方向上的聚酰亚胺薄膜的厚度、热导率、截面积,根据文献[21],热导率ins=2.4 W/(m·K)。
需要通过传导热阻将磁心网络与绕组网络相连,由于绕组前端部分的内侧同时接触磁心中柱的上下部分和气隙,需要使用1.3.1节中表面接触多种介质的建模方法;接触空气的表面通过传导热阻和对流热阻连接空气,由于聚酰亚胺薄膜的传导热阻远小于空气对流热阻,为了简化模型,可以忽略绕组接触空气表面上聚酰亚胺薄膜的传导热阻;在与侧面绕组相连的表面上,通过传导热阻实现绕组间的连接。类似的处理同样可以应用于另外三部分绕组,最终得到了绕组前端的等效热阻网络如图8所示,图中,ins1ins2ins3为对应接触面上聚酰亚胺薄膜的传导热阻,b1b2b3为绕组区域的传导热阻。
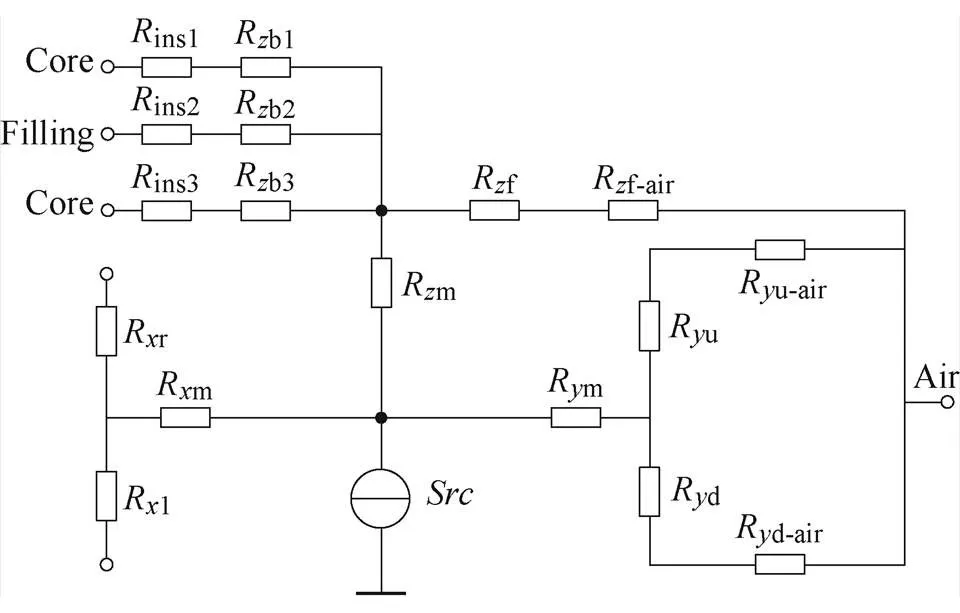
图8 绕组前端的等效热阻网络
在实验中,往往需要在电感内部埋置温度传感器进行温度测量,温度传感器或许会对电感的温度分布造成影响。由于本文使用PT100铂热电阻作为温度传感器,几何尺寸为2.3 mm×2.1 mm×0.9 mm,相对于绕组区域很小,且对模型计算结果几乎没有影响,可以忽略温度传感器热阻对结果的影响。
1.3.4 窗口内空气区域处理
在磁性元件的实际运行中,其磁心窗口区域内的空气温度会升高,若将空气视作恒温,会对热分析结果造成影响,且随着磁心体积减小,影响会加大。为了提高热阻网络的计算精度,本文将磁心窗口内的空气视作两个长方体块,利用图7的热阻网络对其建模,并添加到整体热阻网络模型中。
1.3.5 磁心损耗计算
文献[22]提出,非正弦激励时,在磁通密度波形为分段线性的情况下,磁心的铁损密度可以表示为
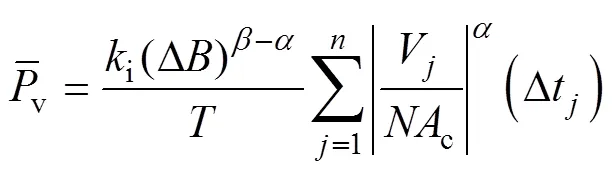
其中
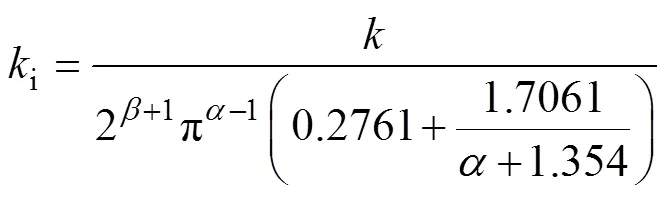
式中,i、、为标准正弦激励下Steinmetz公式中的系数;D为一个周期内磁通密度的峰-峰值(T);为绕组匝数;c为磁心有效截面积;为波形的周期;为一个周期中划分时间段个数;Dt为第时间段的时间长度;V为第时间段的绕组端电压。
文献[18]认为磁心中损耗均匀分布,采用平均损耗密度分布方式,每一子区域的磁心损耗和该区域体积成正比。本文考虑磁通密度在磁心中的不均匀分布,即磁心中损耗密度并非处处相等,利用有限元法分析磁心内部的磁通密度分布,如图9所示,由此积分得到了磁心各个区域的损耗密度比例,有限元计算使用COMSOL 5.6软件,选择直接求解器MUMPS,相对容差设置为0.001,单次计算耗时4 s。按照比例将总磁心损耗分配到各个子区域,实现更加接近实际的磁心损耗计算,表1展示了平均损耗密度分布与考虑实际损耗密度分布两种情况下磁心各分块区域损耗的占比。
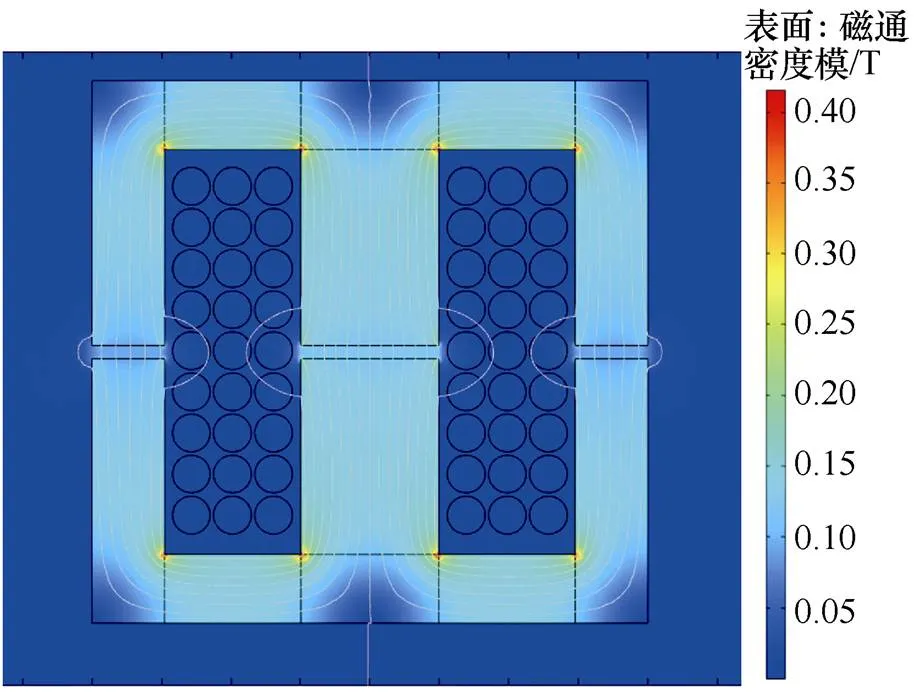
图9 磁通密度二维分布
1.3.6 绕组损耗计算
本文采用文献[23]提出的Tourkhani模型对利兹线的交流绕组损耗w进行计算,即
表1 损耗分布对比
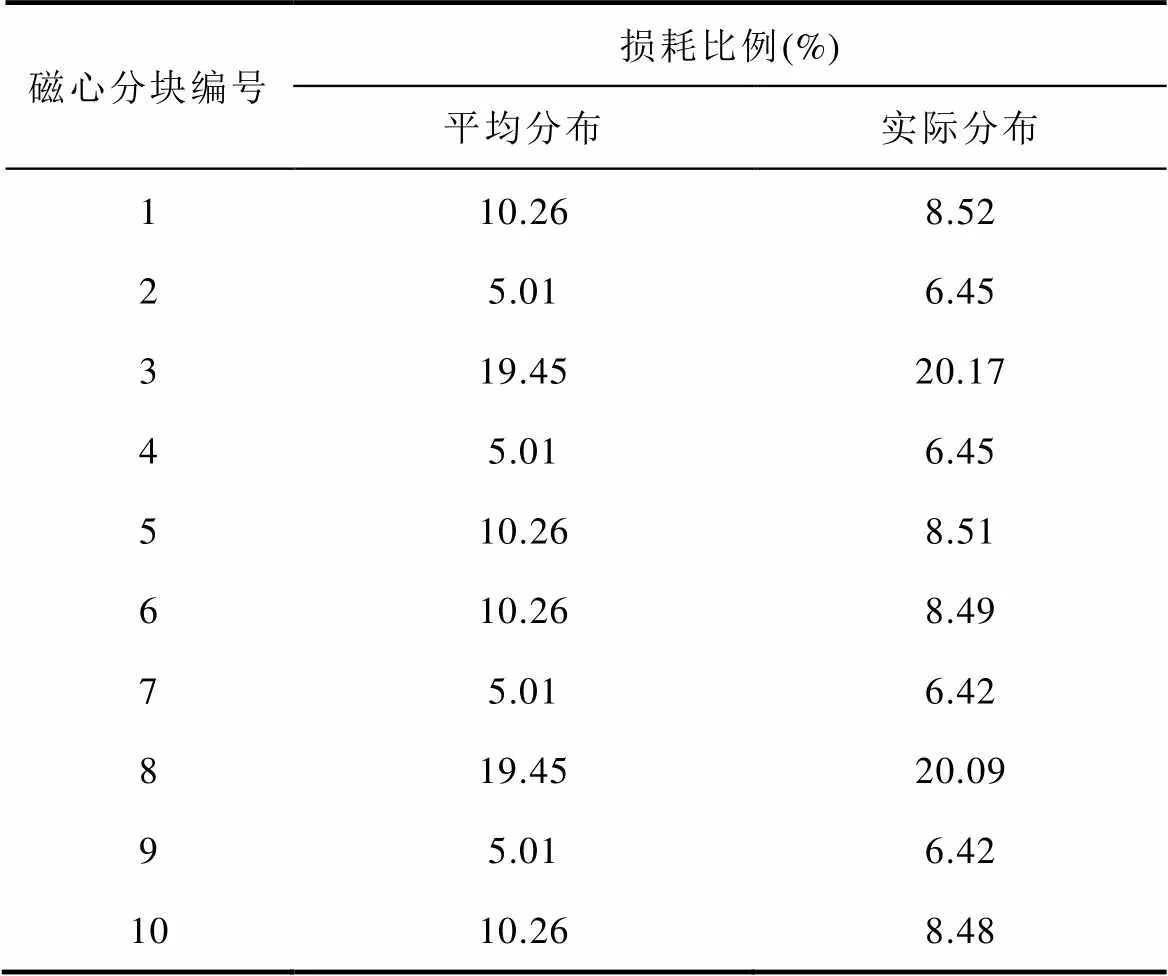
Tab.1 Comparison of loss distribution
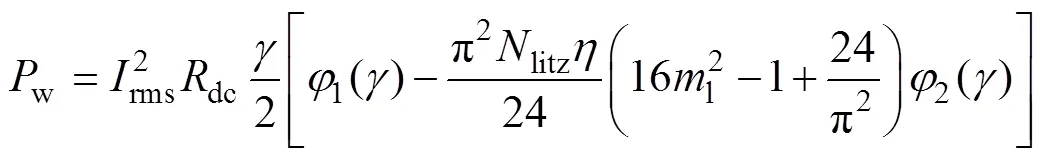
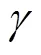
对于绕组电流非正弦的情况,根据文献[24],可以对电流进行傅里叶分解后分别计算基波、各次谐波的交流绕组损耗,求和后可得总交流绕组损耗。
1.4 综合考虑热各向异性与多种传热方式的电感整体热阻网络模型
按照1.3节提出的建模方法,对实际EE型电感进行热阻网络建模,得到如图10所示的精确热阻网络模型,其中各矩形区域均采用图1所示三轴九热阻网络模型建模,空气热阻和绝缘热阻通过外部连接实现。
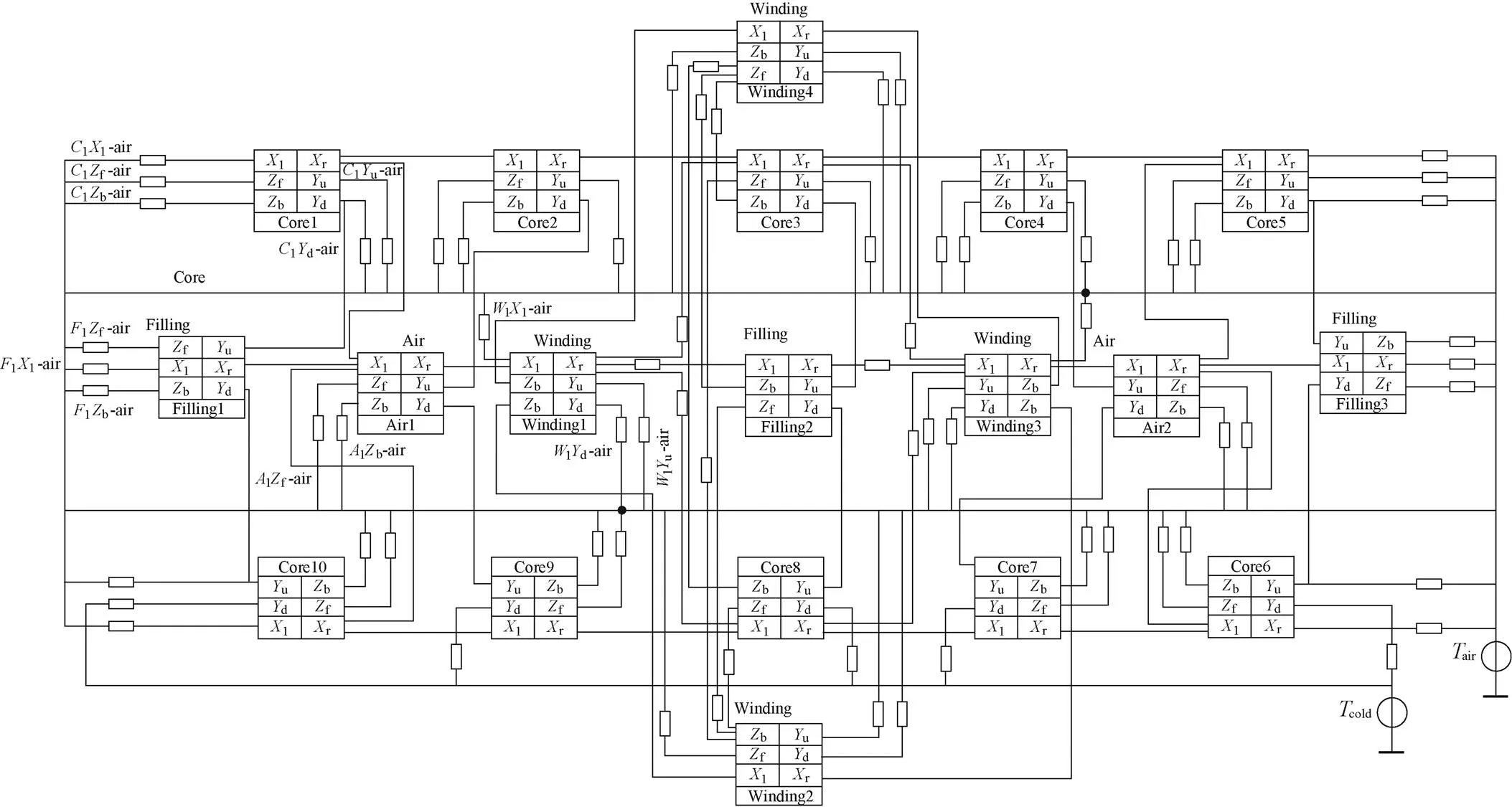
图10 电感集总参数热阻网络
区域名称中的Core、Filling、Winding、Air分别表示磁心、气隙填充材料、绕组和空气块,后缀表示子区域编号,Core1表示磁心中编号为1的子区域。每一个子区域中的rl、u、d、f、b分别为图4所示坐标系下长方体每个面对应的热阻网络结点。下面以磁心区域1为例说明热阻网络精确模型与实际电感器件之间的对应关系。
根据图4的区域划分示意图,Core1子区域的l、u、f、b均为直接接触空气表面,故对应结点通过对流热阻和辐射热阻的并联热阻连接至环境温度热源。Core1子区域的r表面同时接触Core2的l表面和空气块Air1的l表面,根据1.3.1节提出的表面同时接触多种介质情况的处理方法,Core1子区域的区域热阻网络建模同图6。
除此之外,由于磁心和绕组内部存在热源,而气隙填充物和空气块中不存在热源,分别利用图1、图7所示的热阻网络建模。
1.5 热阻网络迭代求解
根据建立的综合考虑热各向异性与多种传热方式的电感整体热阻网络模型,使用Matlab编写计算程序。由于对流热阻和辐射热阻均与磁心表面温度有关,而实际温度未知,无法在建立模型时求出对流、辐射热阻的准确大小,故需要迭代计算。同时由于磁心损耗和绕组损耗均与温度有关,需要添加温度对损耗的影响,根据磁心材料数据手册,通过数据点拟合得到磁心损耗随温度的变化关系为
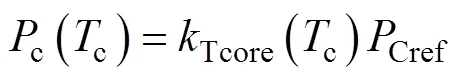
其中
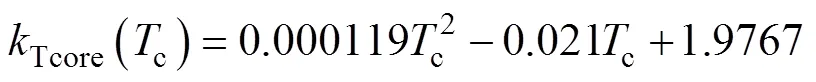
式中,Cref为温度在100℃下式(14)得到的磁心损耗结果;c为磁心温度(℃)。
根据文献[25],铜的温度系数为0.004 1×10-6/℃,计算出绕组损耗随温度的变化为

式中,Wref为温度在70℃下式(16)得到的绕组损耗结果;w为绕组温度(℃)。
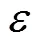

图11 模型计算流程
2 实验研究
2.1 实验平台搭建
通过对功率电感在交流方波电压信号下的热分析,验证本文提出的精确热阻网络模型的准确性。搭建如图12所示的功率电感实验平台。

图12 实验平台
为了模拟真实的应用场景,将电感磁心下表面通过导热硅脂连接至水冷板,水冷板保持恒温。温度测量使用PT100热敏电阻和测温枪设备,实现了磁心各子区域表面温度的测量。
2.2 实验工况
在表2记录的三种电压工况下进行实验,表中,H桥输出方波频率设定为50 kHz。水冷板设定温度cold=18 ℃,实验环境温度air=19.65 ℃。
表2 实验工况

Tab.2 Experiment conditions
2.3 实验结果
研究稳态时电感的温度分布,在三种工况下测量磁心各子区域的温度,通过计算得到各磁心区域的平均温度,再计算实验测量结果与理论热阻网络计算结果之间的相对误差,可得实验结果如图13所示。
从结果来看,p590 V工况下磁心区域2、4的理论结果与实验结果相对误差绝对值大于10 %,剩余结果的相对误差绝对值均小于10 %。分析p590 V工况下磁心区域2、4误差相对较高的原因:两处区域进行散热的主要方式为空气散热,即热对流和热辐射。在本文的实验条件下,对流传热方式为自然对流。在此基础上,瑞利数计算等针对对流传热的状态估计会直接影响热阻大小,从而对温度预测结果造成影响,相较于其他工况,p590 V工况下磁心温度较高,周围空气状态估计所造成的误差更高。除此之外,对流、辐射热阻计算公式的精度也会对结果造成影响[18],且相较于其他区域,在以热对流、热辐射为主要散热方式的两处区域中,对流、辐射热阻计算公式的精度对温度预测结果的影响更严重。
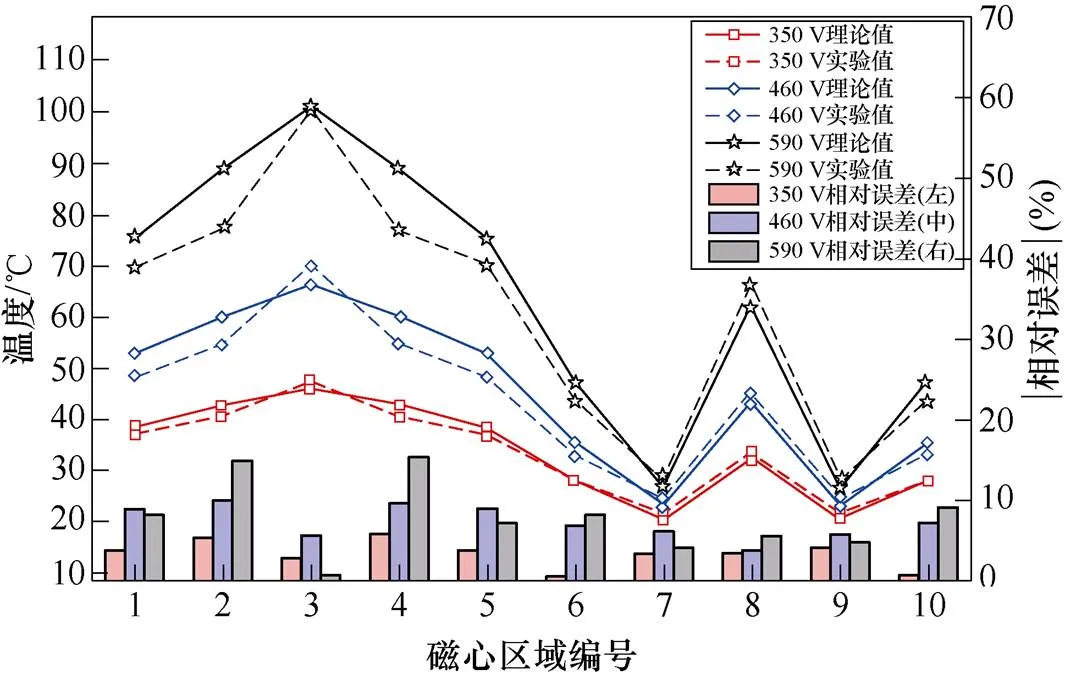
图13 实验结果
对实验中的误差来源进行分析,实验与理论的误差可以分为操作误差和系统误差。其中操作误差由实验的温度测量环节引入,对于磁心的每一个子区域,准确测量其平均温度非常困难,实验时只能通过测量多个点取平均值的方法减小测量误差。系统误差为热阻网络模型导致的误差,以长方体器件的三轴九热阻网络为例,表面的温度分别用各自的平均值表示,这种处理方法使其表面不存在平行于表面的热流,进而导致结果上存在一定误差。
在p=590 V工况下分析实际损耗分布对结果精度的影响,比较平均损耗密度分布与实际损耗密度分布两种情况下的相对误差,考虑不同损耗分布情况的实验结果如图14所示。
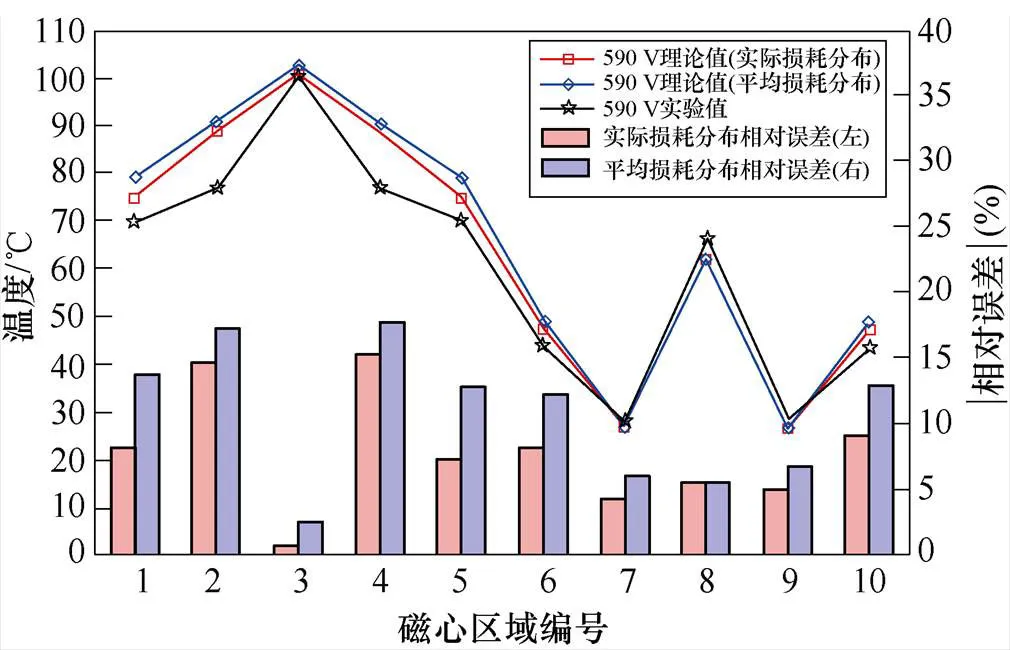
图14 考虑不同损耗分布情况的实验结果
对比两种结果的相对误差,对于磁心子区域8,考虑平均损耗密度分布结果的相对误差略小于考虑实际损耗密度分布的情况;而对于其他子区域,考虑实际损耗密度分布温度结果的相对误差均小于平均损耗密度分布的情况。由此得出结论,在本文提出的热阻网络计算模型中,对实际损耗密度分布的考虑可以提升热阻网络模型计算精度。
在p=590 V工况下分析材料热各向异性热导率对结果精度的影响。利用文献[18]的绕组材料热各向同性方法对温度结果分析,取绕组区域的热各向同性热导率为0.41 W/(m·K),比较本文热各向异性方法和文献热各向同性方法,考虑材料热各向同性对结果的影响如图15所示。

图15 考虑材料热各向同性对结果的影响
从结果来看,对于区域2、4、7、8、9,考虑材料热各向同性的方法结果的相对误差绝对值更低,其他区域中考虑材料热各向同性方法结果的相对误差绝对值更高。本文结果和文献结果中的相对误差绝对值平均值分别为7.81 %和7.89 %。然而,对区域3来说,相对误差绝对值从0.621 %增加到了3.521 %,由于区域3的温度预测结果是磁性元件工作可靠性的重要判断标准,低于实验结果的预测结果会影响磁性元件工作可靠性的判断。故可得出结论,考虑材料热各向异性对热阻网络模型的提升是有意义的。
3 热阻网络建立规律
对于一个使用EE、EI、UU等典型磁心设计的磁性元件,利用热阻网络模型进行热分析可按如下步骤进行:
(1)热阻网络子区域划分。
(2)区域热阻网络建立。
(3)子热阻网络互联,设定初值,迭代求解。
步骤(1)根据实际情况将复杂的不规则磁性元件拆分为规则区域的组合。对于磁心,通常将其按照磁轭、磁柱进行区域划分;对于绕组,可以按照所绕磁柱的四面分别建模为4个长方体块。而对于内部存在空气的复杂器件,需要根据空气对热分析结果的影响程度决定是否将其看作恒温源。需要注意的是,计算精度和计算时间与区域划分的精细程度有关,为了提升计算速度,通常希望在精度损失较小的条件下减少区域划分个数。对于气隙、拐角等需要独立建模的区域,单独分块。步骤(2)核心在于将热传导、热对流、热辐射三种主要热效应等效为热阻纳入模型中,从而建立各子区域的热阻网络。对于传导热阻、对流热阻、辐射热阻的连接问题,需要分析传热过程。以磁心为例,热流通过传导热阻到达其表面,然后同时通过热对流与表面热辐射两种方式流入空气。结合仿真分析,对流热阻、辐射热阻并联后再与传导热阻串联的处理方式最接近实际情况。步骤(3)则是根据器件实际形状将子区域热阻网络每一个轴向两侧的热阻与空气热源或相邻结构相连,形成计算模型。最后通过迭代法计算得到热分析结果。
4 结论
本文在三轴九热阻网络的基础上,综合考虑材料热各向异性与热传导、热对流、热辐射三种传热方式,以EE型电感元件为例进行了精确热阻网络模型的建立与理论计算,结果与实验较为吻合,得到以下结论:
1)考虑材料热各向异性和多种传热方式的热阻网络模型更符合磁性元件实际运行状态下的温度场分布。
2)相比于文献[18]中平均分布的损耗场模型,利用数值法计算得到的真实损耗场分布结果可以进一步提高模型的运算精度。
综合来看,本文在一定程度上解决了现有热分析模型的部分问题,为实际磁性元件的散热设计提供了参考。尽管如此,本文的研究还有很多可能的改进方向,包括但不限于气隙热等效建模的优化,可以考虑边缘效应和漏磁通对气隙附近磁通密度的影响。在未来,可以基于本文的精确热阻网络模型进行更加全面的温度场解析分析,得到更精确的温度场计算结果,为磁性元件的散热设计提供更可靠的参考。更进一步地,磁性元件的整体优化设计需要综合考虑散热、绝缘、电气参数等多方面的优化,往往需要分析几十万甚至上百万个设计点。在散热优化设计方面,本文所提出的热阻网络解析模型平均单次运算时间约为4 s,保证精度的同时可以满足设计中大量计算设计点的需求,为磁性元件的整体优化设计提供一种有效的实现方式。
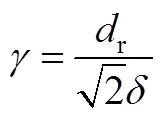


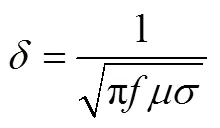
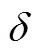
[1] 孙鹤, 李永建, 刘欢, 等. 非正弦激励下纳米晶铁心损耗的计算方法与实验验证[J]. 电工技术学报, 2022, 37(4): 827-836.
Sun He, Li Yongjian, Liu Huan, et al. The calculation method of nanocrystalline core loss under non- sinusoidal excitation and experimental verification[J]. Transactions of China Electrotechnical Society, 2022, 37(4): 827-836.
[2] Bahmani M A, Thiringer T, Rabiei A, et al. Com- parative study of a multi-MW high-power density DC transformer with an optimized high-frequency mag- netics in all-DC offshore wind farm[J]. IEEE Transactions on Power Delivery, 2016, 31(2): 857- 866.
[3] Villar I, Mir L, Etxeberria-Otadui I, et al. Optimal design and experimental validation of a medium- frequency 400kVA power transformer for railway traction applications[C]//2012 IEEE Energy Con- version Congress and Exposition, Raleigh, NC, USA, 2012: 684-690.
[4] 王佳宁, 邹强, 胡嘉汶, 等. 一种中压绝缘大功率中频变压器的优化设计方法[J]. 电工技术学报, 2022, 37(12): 3048-3060.
Wang Jianing, Zou Qiang, Hu Jiawen, et al. An optimal design method for medium-voltage insulated high-power medium-frequency transformer[J]. Transa- ctions of China Electrotechnical Society, 2022, 37(12): 3048-3060.
[5] 李子欣, 高范强, 赵聪, 等. 电力电子变压器技术研究综述[J]. 中国电机工程学报, 2018, 38(5): 1274- 1289.
Li Zixin, Gao Fanqiang, Zhao Cong, et al. Research review of power electronic transformer techno- logies[J]. Proceedings of the CSEE, 2018, 38(5): 1274-1289.
[6] Kolar J W, Bortis D, Neumayr D. The ideal switch is not enough[C]//2016 28th International Symposium on Power Semiconductor Devices and ICs, Prague, Czech Republic, 2016: 15-22.
[7] 李伟力, 付敏, 周封, 等. 基于流体相似理论和三维有限元法计算大中型异步电动机的定子三维温度场[J]. 中国电机工程学报, 2000, 20(5): 15-18, 22.
Li Weili, Fu Min, Zhou Feng, et al. Calculation of 3D stator temperature field of large and medium scale asynchronous motor on the basis of theory of fluid similarity and 3D FEM[J]. Proceedings of the CSEE, 2000, 20(5): 15-18, 22.
[8] 李伟力, 周封, 侯云鹏, 等. 大型水轮发电机转子温度场的有限元计算及相关因素的分析[J]. 中国电机工程学报, 2002, 22(10): 85-90.
Li Weili, Zhou Feng, Hou Yunpeng, et al. Calculation of rotor temperature field for hydro-generator as well as the analysis on relevant factors[J]. Proceedings of the CSEE, 2002, 22(10): 85-90.
[9] 袁发庭, 吕凯, 刘健犇, 等. 基于电磁-热-结构多物理场耦合的铁心电抗器线圈结构优化方法[J]. 电工技术学报, 2022, 37(24): 6431-6441.
Yuan Fating, Lü Kai, Liu Jianben, et al. Coil structures optimization method of iron core reactor based on electromagnetic-thermal-structure multi- physical field coupling[J]. Transactions of China Electrotechnical Society, 2022, 37(24): 6431-6441.
[10] 李永建, 闫鑫笑, 张长庚, 等. 基于磁-热-流耦合模型的变压器损耗计算和热点预测[J]. 电工技术学报, 2020, 35(21): 4483-4491.
Li Yongjian, Yan Xinxiao, Zhang Changgeng, et al. Numerical prediction of losses and local overheating in transformer windings based on magnetic-thermal- fluid model[J]. Transactions of China Electro- technical Society, 2020, 35(21): 4483-4491.
[11] 谢颖, 胡圣明, 陈鹏, 等. 永磁同步电机匝间短路故障温度场分析[J]. 电工技术学报, 2022, 37(2): 322-331.
Xie Ying, Hu Shengming, Chen Peng, et al. Thermal field analysis on inter-turn short circuit fault of permanent magnet synchronous motor[J]. Transa- ctions of China Electrotechnical Society, 2022, 37(2): 322-331.
[12] 朱艺锋, 葛琼璇, 刘育红, 等. 75kVA三电平背靠背变流器的散热分析及优化[J]. 电工技术学报, 2012, 27(2): 103-108.
Zhu Yifeng, Ge Qiongxuan, Liu Yuhong, et al. Analysis and optimization of cooling system for 75kVA three-level back-back converter[J]. Transa- ctions of China Electrotechnical Society, 2012, 27(2): 103-108.
[13] 兰志勇, 魏雪环, 李虎如, 等. 基于集总参数热网络法的永磁同步电机温度场分析[J]. 电气工程学报, 2017, 12(1): 17-21, 32.
Lan Zhiyong, Wei Xuehuan, Li Huru, et al. Thermal analysis of PMSM based on lumped parameter thermal network method[J]. Journal of Electrical Engineering, 2017, 12(1): 17-21, 32.
[14] 张建忠, 姜永将. 基于等效热网络法的定频双转子永磁风力发电机的热分析[J]. 电工技术学报, 2015, 30(2): 87-97.
Zhang Jianzhong, Jiang Yongjiang. Thermal analysis of constant frequency double rotor permanent magnet generator based on equivalent thermal network method[J]. Transactions of China Electrotechnical Society, 2015, 30(2): 87-97.
[15] 王晓远, 高鹏. 等效热网络法和有限元法在轮毂电机温度场计算中的应用[J]. 电工技术学报, 2016, 31(16): 26-33.
Wang Xiaoyuan, Gao Peng. Application of equivalent thermal network method and finite element method in temperature calculation of in-wheel motor[J]. Transa- ctions of China Electrotechnical Society, 2016, 31(16): 26-33.
[16] 万萌, 应展烽, 张旭东, 等. 功率器件集总参数热路模型及其参数提取研究[J]. 电工技术学报, 2015, 30(21): 31-38.
Wan Meng, Ying Zhanfeng, Zhang Xudong, et al. Research on the lumped parameter thermal circuit model and the parameter extraction method of power devices[J]. Transactions of China Electrotechnical Society, 2015, 30(21): 31-38.
[17] Leibl M, Ortiz G, Kolar J W. Design and experimental analysis of a medium-frequency transformer for solid- state transformer applications[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2017, 5(1): 110-123.
[18] Mogorovic M, Dujic D. Thermal modeling and experimental verification of an air cooled medium frequency transformer[C]//2017 19th European Con- ference on Power Electronics and Applications, Warsaw, Poland, 2017: 1-9.
[19] Wrobel R, Mellor P H. A general cuboidal element for three-dimensional thermal modelling[J]. IEEE Transa- ctions on Magnetics, 2010, 46(8): 3197-3200.
[20] Simpson N, Wrobel R, Mellor P H. Estimation of equivalent thermal parameters of impregnated electrical windings[J]. IEEE Transactions on Industry Applications, 2013, 49(6): 2505-2515.
[21] 查俊伟, 王帆. 高导热聚酰亚胺电介质薄膜研究进展[J]. 物理学报, 2022, 71(23): 190-207.
Zha Junwei, Wang Fan. Research progress of high thermal conductivity polyimide dielectric films[J]. Acta Physica Sinica, 2022, 71(23): 190-207.
[22] Venkatachalam K, Sullivan C R, Abdallah T, et al. Accurate prediction of ferrite core loss with non- sinusoidal waveforms using only Steinmetz para- meters[C]//2002 IEEE Workshop on Computers in Power Electronics, Mayaguez, PR, USA, 2003: 36-41.
[23] Tourkhani F, Viarouge P. Accurate analytical model of winding losses in round Litz wire windings[J]. IEEE Transactions on Magnetics, 2001, 37(1): 538- 543.
[24] Ferreira J A. Analytical computation of AC resistance of round and rectangular litz wire windings[J]. IEE Proceedings B (Electric Power Applications), 1992, 139(1): 21.
[25] 谢文旺, 周尚礼, 吴昊文, 等. 基于不同材料温度系数差异的测温研究[J]. 自动化与仪器仪表, 2022(5): 49-52.
Xie Wenwang, Zhou Shangli, Wu Haowen, et al. Research on temperature measurement based on the difference of temperature coefficients of different materials[J]. Automation & Instrumentation, 2022(5): 49-52.
An Accurate Thermal Resistance Network Model for Magnetic Elements Considering Thermal Anisotropy of Materials and Various Heat Transfer Ways
(State Key Laboratory of Control and Simulation of Power System and Generation Equipment Tsinghua University Beijing 100084 China)
The development trend of magnetic components is higher frequency, smaller volume, and higher power density. With the increase of power density, heat dissipation becomes a key factor affecting the reliable operation of magnetic components, which puts forward higher requirements for the thermal analysis of magnetic components. The traditional thermal analysis models have problems such as long calculation time and single heat transfer way. In addition, the thermal anisotropy, different distribution of loss density in magnetic core and interaction effect between temperature and loss are usually ignored. A precise and generalized analytical thermal modeling method is needed to meet the calculation requirements of the magnetic component optimization design and match the actual working condition with complex heat dissipation ways. The inductor made of an EE-type magnetic core is taken as an example, and the three-axis nine-thermal-resistance network model with thermal anisotropy is introduced for solving the heat conduction problem. A three-axis fifteen-thermal-resistance network model was proposed considering multiple heat transfer ways, thermoelectric coupling, material thermal anisotropy, and actual loss distribution of magnetic core. For multiple heat transfer ways, the influence of heat conduction, heat convection, and heat radiation should be considered because high-power density magnetic components are often used with water cooling, air cooling, or other cooling structures. Moreover, the influence of heat convection and heat radiation has been considered in the model as air thermal resistances. The magnetic field distribution influences the loss density distribution in each area. The loss distribution of the magnetic core is calculated by the 2D finite element simulation of the actual magnetic field to match the actual condition. The loss of winding and magnetic core requires iterative calculation because the temperature affects the magnetic core’s iron loss density and copper’s electrical conductivity. In contrast, the winding loss and magnetic core loss affect the temperature. In addition, the thermal anisotropy is considered in the model. The conduction thermal resistances of different axes in the Cartesian coordinate system are calculated by different thermal conductivities due to thermal anisotropy. At the frequency of 50 kHz, three working conditions ofp=350 V,p=460 V, andp=590 V were selected to verify the model. The results show that the max relative error for calculating the magnetic core temperature is no more than 14%, and the max relative error in the highest temperature area of the magnetic core is no more than 6% under three working conditions. Compared with other thermal resistance network models, the precision of the thermal resistance network model can be improved by considering the material thermal anisotropy, thermoelectric coupling, and actual distribution of core loss. The single calculation time of the model can be reduced from several hours in 3D finite element simulation to almost one millisecond in the thermal resistance network. The total calculation time of the thermal resistance network model can meet the time requirement of calculating a large number of design points for optimizing a specific structure magnetic core. Based on the comprehensive thermal resistance network model, a general thermal modeling method is summarized for magnetic components composed of EE, EI, UU, and other typical magnetic cores. The thermal equivalent modeling of the air gap, edge effect, and leakage flux on flux density near the air gap can be considered in the model in the future. A more comprehensive analytical analysis of the temperature field can be carried out, and more precise temperature field calculation results can be obtained, providing a more reliable reference for the heat dissipation design of magnetic components.
Magnetic device, thermal anisotropy of the material, multiple heat transfer modes, actual loss distribution, lumped-parameter thermal resistance network
10.19595/j.cnki.1000-6753.tces.230072
TM47
2023-01-18
2023-03-15
郭 轩 男,1996年生,博士研究生,研究方向为磁性元件和电力电子变压器的建模及优化。E-mail: guo-x18@mails.tsinghua.edu.cn
郑泽东 男,1980年生,副教授,博士生导师,研究方向为电力电子与电气传动。E-mail: zzd@mail.tsinghua.edu.cn(通信作者)
(编辑 陈 诚)

