暗纹东方鲀幼鱼体质量与形态性状的相关与通径分析

孙侦龙，宗巍巍，韩世询，吴爱君，叶建华

[1.江苏中洋集团股份有限公司，江苏 南通 226600；2.中洋种业（江苏）有限公司，江苏 南通 226600]

暗纹东方鲀（Takifugu fasciatus）是我国传统名贵和特色鱼类，为“长江三鲜”之首，鱼肉丰腴鲜美，营养丰富，具有很高的食用价值、经济价值以及文化价值[1]。由于野生暗纹东方鲀体内含有剧毒的神经毒素——河鲀毒素[2-3]，我国相关法律法规明令禁止人们食用包括暗纹东方鲀在内的野生河鲀。随着2014年国家卫生健康委员会批准了养殖暗纹东方鲀为新食品原料、2016年原农业部与原国家食品药品监督管理总局有条件放开了养殖暗纹东方鲀的加工经营，人们对养殖暗纹东方鲀的消费需求越发旺盛，暗纹东方鲀养殖规模也快速扩大。2021年，全国暗纹东方鲀养殖产量为14 559 t[4]，达到2014年暗纹东方鲀养殖产量的3.02 倍[5]。

在水产养殖行业中，良种是养殖成功的先决条件和基础。对于养殖对象而言，生长速度往往是重要的经济指标之一。因此，养殖对象的体质量成为选育的重要目标性状[6]。然而，实际操作中，测量体质量容易受到客观环境因素干扰，影响选育效果。通径分析是在相关分析的基础上，研究形态性状对体质量直接与间接作用的关系及重要性，该方法目前已在翘嘴鳜（Siniperca chuatsi）[7]、克氏原螯虾（Procambarus clarkii）[8]、波行龙虾（Panulirus homarus）[9]、紫石房蛤（Saxidomus punpuratus）等众多鱼、虾、贝等水产品种选育实践中证明可行[10]。孟乾等[11]通过通径分析表明，体长、体高和尾柄高是影响4月龄斑石鲷（Oplegnathus punctatus）体质量的主要形态性状；韦嫔媛等[12]通过通径分析表明，选育高产香港牡蛎（Crassostrea hongkongensis）时，应以壳高这一形态性状为主要选育参考指标。张年国等[13]研究表明，在脊尾白虾（Exopalaemon carinicauda）低盐种群亲本选育时，应以尾节长和头胸甲长为重点选择性状；文献[14-15]研究显示，相关的通径分析，对水产良种选育具有重要的指导意义和科学价值。

目前，对暗纹东方鲀的研究主要集中在人工繁养殖技术[16]、河鲀毒素控毒与利用[17]、性别控制[18]及基因学[19]等方面，关于暗纹东方鲀体质量与形态性状之间相互关系相关的育种基础研究还未见报道。现以40日龄暗纹东方鲀幼鱼为研究对象，利用相关分析和通径分析，研究影响其体质量的主要形态性状，并结合逐步回归分析，建立形态性状对体质量的回归方程，以期为暗纹东方鲀人工选育寻找有效形态性状指标，指导暗纹东方鲀人工选育。

1 材料与方法

1.1 时间与地点

2023年1月29日。地点位于江苏中洋集团股份有限公司海安总部基地。

1.2 材料

暗纹东方鲀幼鱼由江苏中洋集团股份有限公司旗下养殖公司提供。随机选取40日龄暗纹东方鲀幼鱼约350 尾，暂养于公司研发中心试验桶内。暂养条件与公司苗种培育池保持一致，水温24～25 ℃，ρ（溶解氧）＞5 mg/L。暂养期间不投喂饲料，每日换水30%。

1.3 指标测量

暂养48 h 后，用麻醉剂MS-222 麻醉暗纹东方鲀幼鱼，测定其体质量（Y）以及10 个形态性状:全长（X1）、体长（X2）、头长（X3）、吻长（X4）、口裂（X5）、眼间距（X6）、躯干长（X7）、体高（X8）、尾柄长（X9）、尾柄高（X10）。体质量采用电子天平（上海友声，BS300+）称量，精确到0.01 g；形态性状采用数显游标卡尺（浙江得力，DL 312150）测量，精确到0.01 mm。

1.4 数据处理

数据处理根据文献[20]的方法，采用SPSS Statistics 17.0 软件包，对暗纹东方鲀幼鱼的体质量与形态性状进行统计以及相关分析、通径分析，得到相关系数、通径系数等，确定其各形态性状对体质量的直接和间接作用。然后通过逐步引入-剔除法，构建暗纹东方鲀幼鱼形态性状对体质量的多元回归方程，并进行偏回归系数检验。变异系数（CV）的计算公式为:

形态性状对体质量的决定系数，根据文献[21]的计算方法。单个形态性状对体质量决定系数（dj）计算公式为:

式中:Pj——单个形态性状对体质量的通径系数。

2 个形态性状对体质量的共同决定系数（dij）计算公式为:

式中:Pi、Pj——某2 个形态性状分别对体质量的通径系数；

rij——某2 个形态性状的相关系数。

采用SPSS Statistics 17.0 软件进行多远回归分析时，使用的因变量数据，需要服从正态分布。本试验中，试验样本数量（n）= 328，＞30，属于大样本，因此采用Kolmogorov-Smirnov（K-S）方法进行正态分布检验。结果表明，K-S 统计量为0.045，显著水平P=0.20，＞0.05，因此，因变量（Y）服从正态分布，可以进行回归分析。

2 结果与分析

2.1 暗纹东方鲀幼鱼体质量以及形态性状

暗纹东方鲀幼鱼体质量以及形态性状统计分析结果见表1。由表1 可见，暗纹东方鲀幼鱼体质量的CV 为34.95%，大于所选的10 个形态性状的变异系数值（11.15%～17.02%）。

表1 暗纹东方鲀幼鱼体质量以及10 各个形态形状参数的统计结果（n=328）

2.2 暗纹东鲀幼鱼体质量与各个形态性状间的相关分析

对暗纹东方鲀幼鱼体质量以及各个形态性状间进行相关分析，结果见表2。由表2 可见，暗纹东方鲀幼鱼体质量以及各个形态性状间的相关性，均达到了极显著水平（P＜0.01），其中，10 个形态性状中，与Y 相关性最大的形态性状为X1，相关系数达到0.915，与Y 相关性最小的形态性状为X4，相关系数为0.491；10 个形状性状之间，X1与X2之间的相关性最大，相关系数为0.845，X4与X8之间的相关性最小，相关系数仅为0.282。

表2 暗纹东方鲀幼鱼体质量及各个形态性状之间的相关系数①

2.3 暗纹东方鲀幼鱼形态性状对体质量的通径分析

暗纹东方鲀幼鱼形态性状对体质量的通径分析结果见表3。由表3 可知，通过提供选择暗纹东方鲀幼鱼形态性状，采用逐步剔除法得到了7 个模型。其中，模型中决定系数（R2）随着形态性状的引入开始提高，即引入的形态性状，对暗纹东方鲀幼鱼体质量的作用在增大。

表3 暗纹东方鲀幼鱼形态性状模型摘要结果

在模型7 中，R2=0.882，保留了X1、X4、X5、X6、X7、X8和X97 个形态性状。

暗纹东方鲀幼鱼形态性状对体质量相关系数分解汇总见表4。由表4 可见，保留的7 个形态性状对暗纹东方鲀幼鱼体质量通径系数大小依次为:X1、X6、X8、X4、X5、X7、X9。表明X1对暗纹东方鲀幼鱼体质量影响的直接作用最大，而X9对暗纹东方鲀体质量影响的直接作用最小。从间接通径系数中可以发现，形态性状X4、X5、X6、X7、X8和X9，均通过X1对暗纹东方鲀幼鱼体质量有一定的影响，且X1对体质量的相关系数（0.915）是所有形态性状中最高的，因此，X1是对暗纹东方鲀幼鱼体质量影响最大的形态性状。

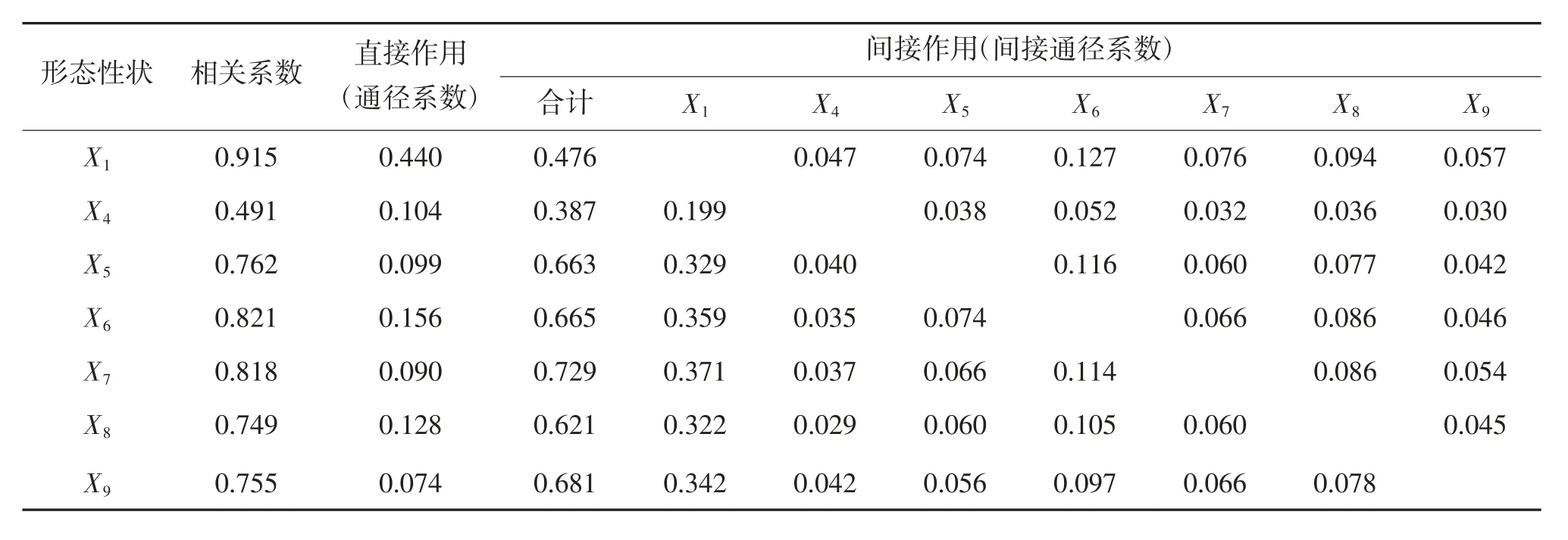
表4 暗纹东方鲀幼鱼形态性状对体质量相关系数分解汇总

2.4 暗纹东方鲀形态性状对体质量决定作用

通过决定系数公式计算，可得到暗纹东方鲀幼鱼单个性状和2 个性状对体质量的决定系数，结果见表5。由表5 可知，单个形态性状和2 个形态性状决定系数综合为0.882，其中，单个形态性状对体质量决定程度最高的为X1（决定系数为0.194），2 个性状对体质量决定程度最高的为X1和X6（决定系数为0.112），说明了X1对暗纹东方鲀幼鱼体质量起主要决定作用。

表5 暗纹东方鲀幼鱼形态性状对体质量决定系数

2.5 多元回归方程的建立

以暗纹东方鲀幼鱼体质量为因变量，形态性状为自变量，选其偏回归平方和贡献量最大的变量，用方差比检验显著性，见表6。由表6 可见，暗纹东方鲀幼鱼X1（t=8.747，P=0.000，＜0.01）、X4（t=4.733，P=0.000，＜0.01）、X5（t=3.166，P=0.002，＜0.01）、X6（t=4.332，P=0.000，＜0.01）和X8（t= 4.388，P=0.000，＜0.01）5 个形态性状回归关系达极显著差异水平，X7（t=2.400，P=0.017，＜0.05）、X（9t= 2.319，P=0.021，＜0.05）2 个形态性状回归关系达显著差异水平，这表明上述7 个形态性状可保留在多元回归方程中。根据表6 中的相关参数，建立暗纹东方鲀幼鱼形态性状对体质量的多元回归方程为:Y=-6.083+0.086X1+0.129X4+0.192X5+0.103X6+0.047X7+0.123X8+0.075X（9R2=0.882）。多元回归方程的回归关系达极显著水平（F=342.738，P=0.000，＜0.01）（表7）。

表6 偏回归系数和回归常数的显著性检验

表7 多元回归方程的方差分析

3 讨论

相关分析主要关注变量之间的相关性，但是结果有一定的局限性，不能确定变量之间的因果关系，只能描述变量之间的关联程度[22]。通径系数是标准化回归方程中的偏回归系数，其值可以为正、负或零，表示变量之间的正向关系、负向关系或没有关系。通径系数的绝对值越大，表示变量之间的关系越强，在数据处理中，优于相关分析和多元回归分析[23]。通径分析则通过建立一个预测模型，包含了多个自变量、中介变量和因变量，能够全面直观地评估直接和间接效应，突出反映不同形态性状对体质量影响的重要性[24]。多元回归分析能进行变量之间因果关系的推断，但需要控制其他变量和考虑潜在的反向因果关系。

3.1 暗纹东方鲀幼鱼形态性状与体质量相关性分析

在对水产养殖对象人工选育时，人们通常将体质量作为重要的选育指标之一，同时结合多种形态性状进行辅助选择，以期得到最优养殖对象[25]。本试验中，暗纹东方鲀体质量的CV（34.95%）远大于形态性状的CV（11.15%～17.02%），表明体质量可作为暗纹东方鲀重要选育指标之一。暗纹东方鲀幼鱼体质量与10 个形态性状相关系数均达到了极显著水平（P＜0.01），即本研究中统计分析的形态形状均间接对暗纹东方鲀幼鱼体质量产生了影响，表明进行更深入的统计分析具有积极意义，这与对小黄鱼（Pseudosciaena polyactis）[26]、大黄鱼（Larimichthys crocea）[27]、大口黑鲈（Micropterus salmoides）[28]等养殖品种的研究结果一致。

3.2 影响暗纹东方鲀幼鱼体质量的主要形态性状

一般来说，相关分析仅考虑了变量间的直接关系，而忽略了变量间的相互影响和间接关系，这可能会导致相关分析的结果具有片面性，所以，有必要在相关分析的基础之上，进行更深入的通径分析和多元回归分析[29]。为克服多变量研究中的多重线性干扰，通常采用逐步引入-剔除法去除偏回归平方和不显著的自变量，把保留的形态性状逐步引入多元回归方程中[30]，在此基础上，当各自变量对因变量的单个决定系数以及两性状决定系数的总和（表示为∑d，数值=R2）≥0.85 时，可得出结论:已经找到对因变量产生主要影响的自变量[31-32]。

由表3 可见，本试验采用逐步引入-剔除法构建了最优模型，该模型保留了暗纹东方鲀幼鱼X1、X4、X5、X6、X7、X8、X97 个形态性状。由表5 可知，模型保留的7 个形态性状对体质量的总决定系数为0.882＞0.85，表明X1、X4、X5、X6、X7、X8、X97 个形态性状，是对暗纹东方鲀体质量产生主要影响的变量。在此基础上，结合通径分析的结果，构建了暗纹东方鲀幼鱼7 个形态性状对体质量的多元回归方程为:Y=-6.083+0.086X1+0.129X4+0.192X5+0.103X6+0.047X7+0.123X8+0.075X9。由表4 可知，X1直接通径系数（0.440）远大于其余形态性状直接通径系数（0.074～0.156）；X4、X5、X6、X7、X8和X9通过X1对体质量产生的间接通径系数均大于对应各形态性状对体质量的直接通径系数，表明在暗纹东方鲀人工选育过程中，可选择X1作为关键形态性状指标，而X4、X5、X6、X7、X8和X9可作为辅助形态性状指标。暗纹东方鲀的全长指标数值越大，说明该暗纹东方鲀个体的几何空间越大，越有利于机体自身营养物质累积存贮，其对应体质量也越大[33]。王新安等[34]在红鳍东方鲀（Takifugu rubripes）类似研究中也有相同的发现。

在暗纹东方鲀以体质量为目标的良种选育中，可考虑以全长为主，吻长、口裂、眼间距、躯干长、体高和尾柄长为辅进行选择。