Investigation of reflection anisotropy induced by micropipe defects on the surface of a 4H-SiC single crystal using scanning anisotropy microscopy

Wei Huang(黄威), Jinling Yu(俞金玲), Yu Liu(刘雨), Yan Peng(彭燕),Lijun Wang(王利军), Ping Liang(梁平), Tangsheng Chen(陈堂胜),Xiangang Xu(徐现刚), Fengqi Liu(刘峰奇), and Yonghai Chen(陈涌海),2,§

1Key Laboratory of Semiconductor Materials Science,Institute of Semiconductors,Chinese Academy of Sciences,Beijing 100083,China

2College of Materials Science and Opto-Electronic Technology,University of Chinese Academy of Sciences,Beijing 100049,China

3National Key Laboratory of Solid-state Microwave Devices and Circuits,Nanjing Electronic Devices Institute,Nanjing 210016,China

4Institute of Micro/Nano Devices and Solar Cells,School of Physics and Information Engineering,Fuzhou University,Fuzhou 350108,China

5State Key Laboratory of Crystal Materials,Shandong University,Jinan 250100,China

Keywords: scanning anisotropy microscopy,SiC,reflection anisotropy,edge dislocation

1.Introduction

A silicon carbide (SiC) single crystal is a typical representative of the third generation of wide band gap semiconductor material with the advantages of large band gap, high breakdown field,high thermal conductivity,high electron saturation velocity, high temperature stability and low dielectric losses.[1-5]The outstanding physical properties of SiC make it suitable for producing high-temperature, high-frequency and high-power devices, and it is becoming a new strategic focus of the global semiconductor industry.[6-8]In the past few decades,much effort has been devoted to achieving large-size,high-quality single crystals of SiC.As crystal growth techniques have developed rapidly, the density of microstructural defects has been reduced greatly.However,it is still an arduous task to completely eliminate them(especially dislocations,micropipes,etc)in SiC single crystals.Moreover,microstructural defects in the semiconductor material directly affect the quality of epitaxial material and the performance of devices,especially high-power devices.[9-12]

In addition to solving the problems of reducing or eliminating microstructural defects such as dislocations and micropipes,it is more important to have a thorough understanding of their formation mechanism.The formation mechanism of micropipes is widely recognized by Frank’s theory,[13]which interprets this formation mechanism as the stress relaxation of screw dislocations with large Burgers vectors.Recently,Ninget al.proposed a hypothesis based on the fact that micropipes are pure screw dislocations to explain the stress birefringence imaging of micropipes.[9]However, Presser,Vetter and Ouisse have demonstrated that the micropipes contain not only screw dislocations with large Burgers vectors but also edge dislocation components by using conventional polarizing microscopy,transmission electron microscopy(TEM)and high-resolution x-ray diffraction(XRD).[14-17]Therefore,controversies still exist over the formation mechanism of micropipes, and it is of great significance to develop a suitable and nondestructive evaluation technique that can fully characterize the micropipe defects and study their formation mechanism, thus providing guidance for the growth of materials.Compared with the methods used in the previous works reported in Refs.[14-17],the method used in this work can obtain information on the microstructural defects by measuring optical anisotropy around them, and it has the advantages of high accuracy,high sensitivity and being non-destructive.

In this paper, we have used scanning anisotropy microscope (SAM) and the micro-Raman technique to characterize the micropipe and investigate its formation mechanism,by studying the optical anisotropy of the micropipe on the surface of 4H-SiC single crystals.The reflection anisotropy(RA) image with a ‘butterfly pattern’ is obtained around the micropipes by SAM.Combining with the micro-Raman technique and theoretical calculations, it is demonstrated that the micropipes consist of edge dislocations.

2.Sample preparation and methods

2.1.Sample preparation

The 4H-SiC single crystal was grown by the sublimation method.[18]The SiC source powder was placed on the bottom of a graphite crucible,and the seed crystal was mounted on the top of the crucible.The SiC source powder was sublimated by heating with an RF generator at a frequency of 10 kHz.The crucible lid was covered with a graphite foil so that it could be used repeatedly.During the crystal growth,the temperature of the crucible lid was kept at 2100°C and the temperature gradient was 50°C·cm-1.In the growth chamber, argon was used as the carrier gas and the chamber pressure was kept at 100-800 mbar.The growth of the 4H-SiC single crystal was terminated after 40 hours and it was cooled to room temperature.Then,4H-SiC wafers were obtained by cutting,grinding and polishing the native SiC crystals; the thickness of each wafer was about 400µm.The surface of a wafer is parallel to the(0001)plane and the polished surface is the Si-polar plane.

Owing to the specific structure of SiC,hollow tubes called micropipes are often found in the sublimation-grown SiC crystal.Micropipes with a size of 0.1-5 µm generally run along thecaxis,and they are fatal for device applications.[9]To observe a high density of micropipe defects, we chose to investigate SiC wafers with defect densities ranging from 5 cm-2to 50 cm-2.A series of metal markers have been placed on the 4H-SiC surface by photolithography and vapor deposition,and they help us find the same measurement area after the rotation of the sample.The sample is ultrasonically cleaned before each measurement.

2.2.Experiments

SAM can measure optical anisotropy images around these microstructural defects based on the photoelasticity effect.[19,20]A schematic diagram of the SAM system is shown in Fig.1, and it is the same as that used in Ref.[21].In the SAM system, two lock-in amplifiers are used in the signal detection system to obtain the normal reflectivity (R) signals and the reflection anisotropy (RA) signals of the 4H-SiC.A solid-state laser with a wavelength of 532 nm and power of 300 mW is used as the light source.After passing through a spatial filter, the laser beam goes through a polarizer and a photoelastic modulator (PEM).Then the beam is split by a polarization-preserving 50/50 beam splitter into an objective lens of long working distance (Mitutoyo 100X, numerical aperture =0.55), and is focused on the sample placed on a piezoelectric ceramic electric translation stage, which can move in two dimensions in a plane.The reflected beam,after passing through the objective lens and the beam splitter,is directed to an analyzer and then focused onto a silicon detector.

The reason why the SAM system is capable of capturing RA images around the micropipe defects is that the micropipe will introduce strain around the micropipe, which will lead to reflection anisotropy around the micropipe.In the SAM system,a PEM together with a polarizer will make the polarization state of the light change periodically between linearly polarized light polarized in thexdirection and polarized in theydirection.By using an analyzer placed after the sample and a lock-in amplifier, we can detect the reflection anisotropy in thexandydirections around the micropipe.Herexandyare the two in-plane orthogonal directions.

The R signal is the intensity signal of reflectivity, which is detected by a lock-in amplifier referenced by a chopper of 220 Hz.The RA signal is the optical anisotropy signal detected by a lock-in amplifier referenced by a PEM of base frequencyω=50 kHz.By changing the position of the light spot on the sample and recording the signal at each position,we can obtain the R mapping and RA mapping of the 4H-SiC.

Raman mapping was also performed in the backscattering configuration at room temperature using a Jobin-Yvon HR Evolution micro-Raman system, equipped with a liquidnitrogen-cooled charge-coupled detector camera.The excitation light is from a diode-pumped solid-state laser with a wavelength of 532 nm.Passing through a×100 microscope objective (numerical aperture=0.90), the light is focused on the sample with a diameter of approximately 1µm and a power of 10 mW.The spectral resolution of the Raman spectrometer is 0.35 cm-1.

2.3.Theory

The SAM system can precisely measure the in-plane optical anisotropy (IPOA) by measuring the relative difference in reflection coefficient between the two in-plane orthogonal directions,denoted asxandy,which is defined as[22-25]

Hererxandryare the reflection coefficients in thexandydirections, respectively.ris the averaged reflection coefficient,i.e.,r=(rx+ry)/2, and Δr=rx-ry.The intensity of the reflected light arriving at the detector can be expressed as

HereR=|rx+ry|2/4 is the reflectivity of the sample,andE20represents the intensity of the reflected light.φis the phase retardation induced by the PEM.J0,J1andJ2are Bessel functions, andωis the base modulation frequency of the PEM.Re(Δr/r) and Im(Δr/r) are the real and imaginary components of Δr/r, respectively.By adoptingφto be 0.383λ, we haveJ0=0.Thus, the R signal of the system is proportional to the intensity of the light recorded by the detector.Since the RA signal varies at a frequency ofω, its intensity is proportional to the imaginary part of Δr/r,reflecting the IPOA of the sample.

Comparing Eq.(3)with Eq.(2),we find that the RA signal is essentially the phase difference between the light polarized in thexdirection and that in theydirection of the detected light,i.e.,Δφ.

Fig.1.Schematic diagram of the SAM system.

3.Results and discussion

3.1.RA images of the SiC micropipe defects

Figure 2 shows the R and RA images of the two micropipes obtained by the SAM system.Figures 2(a) and 2(c) are the R images of the micropipes M1 and M2, respectively.The R image represents the surface topography of the sample,[21]and the blue spot in the middle of the R image indicates the micropipe.The small green spots near the micropipes in the R image have been confirmed to be dust on the surface of the sample.Figures 2(b)and 2(d)are the RA images of M1 and M2, respectively.The RA image of M1 exhibits a butterfly-like pattern with four bright wings (one pair shows positive values,and the other pair negative).The RA image of M2 is similar to that of M1 except that the orientation of the butterfly-like pattern is different.From the discussion below,it can be seen that this is due to the different orientations of the Burgers vectors.

Fig.2.Two typical SAM images of micropipes.(a)and(b)The normal R and RA images of micropipe M1,respectively.(c)and(d)The R and RA images of micropipe M2,respectively.The signal unit in(a)and(c)is 1,and that in(b)and(d)is 10-3.

3.2.Discussion and analysis of the RA image

3.2.1.Theoretical analysis of the RA image

It has been found that RA images are reflection optical anisotropy signals(Δφ)generated at the interface between two different materials, or induced by the height of the step on the nanometer scale,or due to linear defects on the surface of the material.[19,26-28]The RA image of the micropipe may be caused by the strain field around it.The relation between the reflection optical anisotropy signal Δφand the strain tensorεcan be expressed as[29]

Here Δφis the phase difference, which represents the relative difference in reflection coefficient in two perpendicular in-plane directions for each test point.εxx,εyyandεxyare the components of strain tensors.fin Eq.(4)is a complex function,from which we can calculate the RA image,related to the strain field.

Although there are still controversies, it is quite certain that micropipes are related to dislocations.Therefore, it is necessary to theoretically analyze the RA image induced by dislocations.Dislocations include edge dislocations and screw dislocations.For edge dislocations,εxx ̸=0,εyy ̸=0,εzz ̸=0,εxy ̸=0,and the other components are zero,i.e.,the stress tensor induced by the edge dislocation can be expressed as

Obviously, thezaxis is one of the principal axes.Since the SAM system only measures the optical anisotropy in thex-yplane, it is not necessary to take into account the stress component in thezdirection, i.e.,εzz.The eigenequations of the in-plane strain field can be expressed as

and the corresponding eigenvectors are

By substituting the stress tensor of the edge dislocations into Eqs.(10) and (12), we can calculate the RA images with Burgers vectors directed in different directions theoretically,as shown in Fig.3.

The strain field of screw dislocations is much simpler than that of edge dislocations.According to the dislocation theory in reference,[30]the strain component of the screw dislocation can be expressed in polar coordinates as

whereµis the shear modulus andbis the Burgers vector.Here the center of the screw dislocation is set as the origin of the coordinates,andris the distance from the origin.The remaining components are all zero, i.e.,σrr=σrϑ=σrz=0.It can be seen from Eq.(15) that the shear stress component produced by the screw dislocation is inversely proportional tor,and the stress field of the screw dislocation is axisymmetric.Through the conversion relationship between the strain tensor and the stress tensor, it is obvious that the strain components of the screw dislocation in thexandydirections are zero.Therefore, the stress field of the screw dislocation does not cause the IPOA signal between thexandydirections(Δφ=0).

Fig.3.Simulated RA image of the edge dislocations with Burgers vectors in different directions.‘⊥’indicates the direction of the Burgers vector.

3.2.2.Discussion and analysis of the RA image of M1

It can be seen from Fig.2(b) that the RA image shows a typical butterfly-like shape,which is essentially the same as the butterfly-like stress birefringence imaging obtained by the polarization microscope,[9,16]except that the RA image shows a polar distribution.Based on the theory of the photoelastic effect, the RA image is generated by in-plane stressεxxandεxx-εyy.According to the above theoretical analysis of the screw dislocation, it is known that the screw dislocation does not generate an RA signal in thex-yplane(Δφ=0).For the edge dislocations,the non-zero stress components areεxx,εyy,εzzandεxy,i.e.,εxyandεxx-εyyare not zero,leading to an RA signal in thex-yplane(Δφ ̸=0).[31,32]Therefore,the edge dislocation component must be taken into account in the analysis of the RA signal of the micropipes.

To obtain knowledge of the strain distribution around the micropipes,we performed micro-Raman measurements,since the Raman frequency shift of the modes E1(TO) and E2(TO)reflects the strain state of the sample.Figure 4(a) shows the Raman spectrum of the 4H-SiC in a region without micropipes.The peaks of E2(TO), E1(TO) and A1(LO) are located at about 776.5 cm-1, 797.3 cm-1and 965.1 cm-1, respectively, which are consistent with other reports.[33,34]Figure 4(b) shows the peak position mapping of E2(TO) around the M1,and Fig.4(c)shows the mapping of the peak positions of E1(TO)around M1.They all exhibit a dipole-moment-like distribution.Obviously, the peak position of E2(TO) is more sensitive to strain than that of E1(TO),which indicates that the E2(TO)mapping is more accurate for characterizing the strain field.

In Fig.4(b),the redshift or blueshift of the E2(TO)mode is within the range±0.6 cm-1.A compressive strain in the film will reduce the bond lengths and the vibration frequency of atoms, leading to a blueshift of Raman peaks; conversely,a tensile strain will lead to a redshift.Therefore,the red lobe(blueshift) in Fig.4(b) indicates that the area of the film is under compressive strain, while the blue lobe (redshift) suggests that it is under tensile strain.This energy shift is due to elastic lattice deformation by the strain field of the edge dislocation,[35]i.e., on one side of the dislocation the additional lattice plane causes compressive strain,whereas on the opposite side a tensile strain is induced.The strain field distribution indicates that the dislocation is an edge dislocation,and the Burgers vector is directed along thexaxis,as denoted by the ‘⊤’in Fig.4.

Figure 4(d)shows the simulation result of the RA image based on an ideal edge dislocation with the Burger vector directed along thexaxis.Comparing Fig.4(d) with Fig.2(b),one can see that the simulation result shows the same shape as that observed in the experiment,which suggests that the simulation result agrees very well with experimental results.The simulation result confirms our inference about the nature of the micropipes,i.e.,that they are edge dislocations.

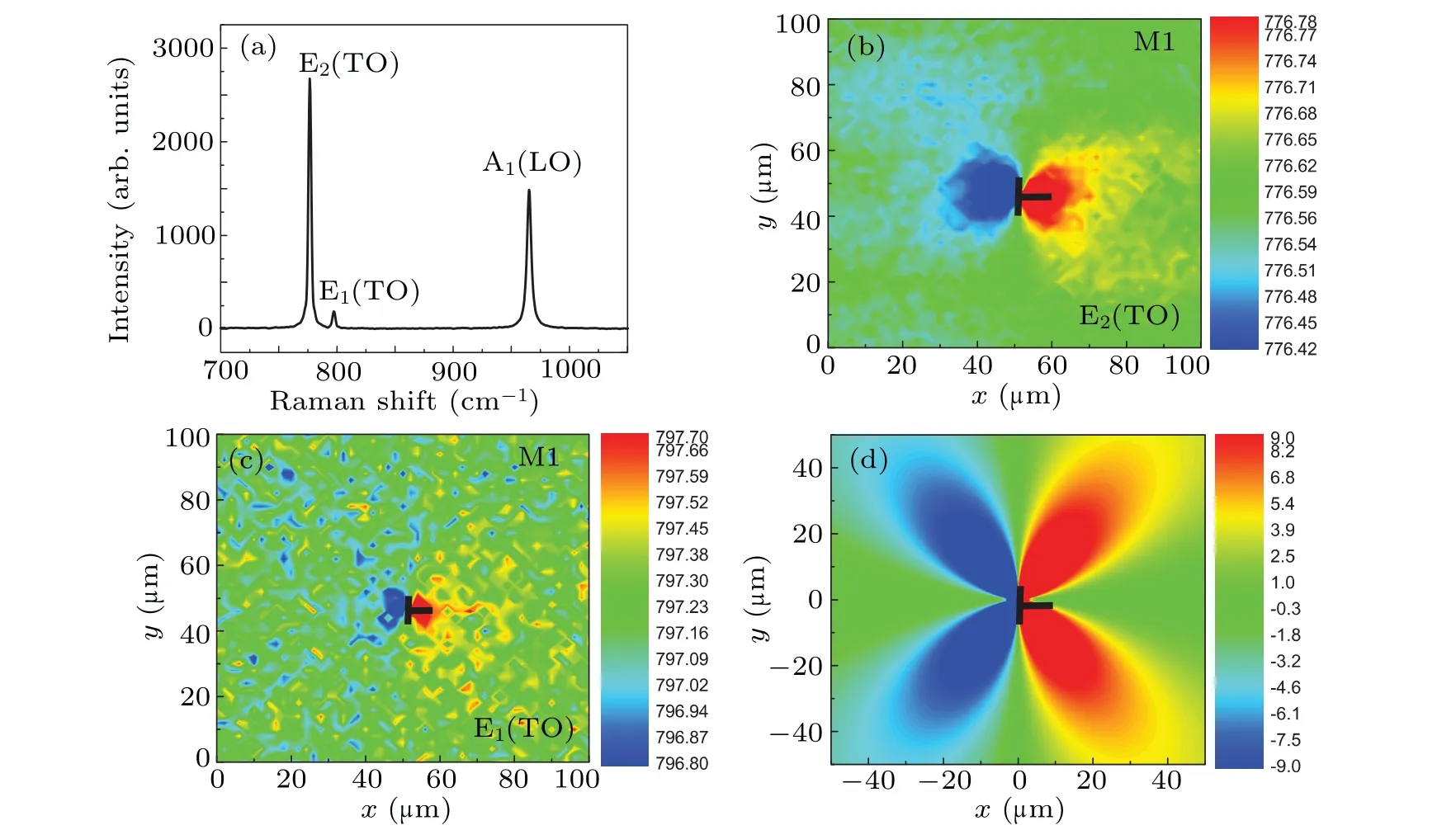
Fig.4.Raman spectra and the simulated RA image around the micropipe M1.(a)Raman spectrum of the 4H-SiC wafer in a region without micropipes.(b)The Raman peak position mapping of E2(TO)mode around the micropipe M1.(c)Raman peak position mapping of E1(TO)mode around the micropipe M1 for an azimuth angle θ of 0°.(d)The simulated RA image around the micropipe M1 when the Burgers vector is in the x direction,which is indicated by the symbol ‘⊤’.

3.2.3.Discussion and analysis of the RA image of M2

Interestingly, the RA image of the micropipe M2 shows different distributions in direction to that of M1.To find out the reason, we measure the Raman mapping of the E2(TO)mode of the micropipe M2,and the result is shown in Fig.5(a).It can be seen from Fig.5(a)that the‘dipole’of M2 shows a 60°rotation compared with that of M1, which indicates that the Burgers vector in M2 is rotated by an angle of 60°, according to the above analysis of the Raman mapping and the RA image.Different orientations of the Burgers vector will lead to the different strain components that show up in the RA images,thus resulting in different RA images.

Figures 5(b) and 5(c) show the stress birefringence images around the micropipe M2 at azimuth anglesθof 0°and 90°,respectively, obtained by the polarization microscope.It can be seen that the polarization microscope also shows different shapes as the sample rotates,but the sign remains the same.This is because the stress birefringence signal obtained by the polarization microscope is proportional to the absolute value of the IPOA.The RA images obtained from the SAM system and the stress birefringence images obtained through polarized microscopy show the same patterns,and both of them change with the orientation of the Burgers vectors.The differences between them are that the RA images exhibit positive and negative values,which makes it easy to distinguish the orientation of the edge dislocations,while the stress birefringence images obtained by polarized microscopy show the same sign,and it is difficult to determine the orientation of the edge dislocations.

Fig.5.(a)Raman peak position mapping of the E2(TO)mode around the micropipe M2.The azimuth angle θ adopted here is the same as that adopted in Fig.2.(b),(c)Stress birefringence images around the micropipe M2 at azimuth angles θ of 0° and 90°,respectively,obtained by the polarization microscope.

Fig.6.Experimental and simulated results of the RA images around the micropipe M2 for different azimuth angles θ.(a)-(c)Experimental results of the RA images at θ of 0°,90°and 120°,respectively.(d)-(f)Simulated results of the RA images at θ of 0°,90°and 120°,respectively.

To further confirm our model,we measure the RA images of the micropipe M2 for different orientations of Burgers vectors,which is achieved by rotating the sample in thex-yplane around the axis that goes through the micropipe.Specifically,we rotate the sample 60°anticlockwise firstly.Thus,the Burgers vector of M2 is directed along thexaxis,which is the same as that of M1.Denoting this azimuth angle as 0°,i.e.,θ=0°,we measure the RA image of M2 for this azimuth angle, as shown in Fig.6(a).Then, after rotating the sample 90°and 120°clockwise,respectively,i.e.,θ=90°and 120°,we measure the RA images correspondingly,and the results are shown in Figs.6(b)and 6(c),respectively.

It can be seen from Fig.6 that the experimental results are essentially in agreement with the theoretical calculation,because they show a similar pattern.The slight difference between experimental data and the theoretical results may be due to the fact that the micropipe is not strictly perpendicular to the surface of the sample, but we do not take this effect into account.Comparing the experimental and theoretical results,we can come to the following conclusions.Firstly,the differences between the RA images of M1 and M2 shown in Figs.2(b)and 2(d),respectively,are caused by the different orientations of the Burgers vectors.When the Burgers vector of M2 is rotated to align in the same direction as that of M1, their RA images show the same shape, which is induced by the IPOA of the strain field due to the edge dislocations.Secondly,only when the Burgers vector is directed along thexoryaxis can the RA image present a butterfly-like shape.Thirdly,the sign of the RA image for a certain area is reversed when the sample is rotated 90°, which is consistent with the observations reported in previous studies.[21,29]

From the above analysis,one can see that the distinct features and characteristics of the RA images for micropipes are that the RA images show a butterfly-like pattern with some‘wings’ positive and other ‘wings’ negative.In essence, micropipes are actually dislocations.Combining with the theoretical calculation, we have demonstrated that the butterflylike RA image is due to the edge dislocation.The shape of the butterfly-like pattern is related to the orientation of the Burgers vectors.By rotating the sample, the RA image will show different patterns.

4.Conclusion

In conclusion,we have investigated the optical reflection anisotropy microscopy mappings of micropipe defects on the surface of a 4H-SiC single crystal by using the SAM system.The RA image with a ‘butterfly pattern’ is obtained around the micropipes with this system.By comparing the experimental results of the RA images with the Raman mapping,we find that the micropipes consist of edge dislocations with relatively large Burgers vectors.Besides, the strain distribution around the micropipes is also deduced.It is revealed that the RA image obtained by SAM shows the same shape as the stress birefringence image obtained by a polarization microscope,but the RA image can distinguish positive and negative stresses.Besides, the resolution of SAM is higher than that of the micro-Raman technique and a polarization microscope.This work further suggests that SAM is a non-destructive,convenient and effective method for studying the microstructural defects on semiconductor material and device surfaces.

Acknowledgements

Project supported by the National Key Research and Development Program of China(Grant Nos.2018YFE0204001,2018YFA0209103,2016YFB0400101,and 2016YFB0402303),the National Natural Science Foundation of China (Grant Nos.61627822, 61704121, 61991430, and 62074036), and Postdoctoral Research Program of Jiangsu Province (Grant No.2021K599C).