A lightweight symmetric image encryption cryptosystem in wavelet domain based on an improved sine map
Baichi Chen(陈柏池), Linqing Huang(黄林青), Shuting Cai(蔡述庭),Xiaoming Xiong(熊晓明), and Hui Zhang(张慧)
1School of Advanced Manufacturing,Guangdong University of Technology,Jieyang 522000,China
2School of Integrated Circuits,Guangdong University of Technology,Guangzhou 510006,China
3School of Automation,Guangdong University of Technology,Guangzhou 510006,China
Keywords: image encryption,discrete wavelet transform,1D-chaotic system,selective encryption,Gaussianization operation
1.Introduction
With the Internet diffusion,images have become the most significant carrier of multimedia information.However, images are susceptible to illegal interception and tampered by attackers when it is distributed on public servers, causing great losses and harm to users.In this context,to secure the image transmission, some technologies like image encryption, image hiding[1,2]and image watermarketing[3]have been widely studied.
In recent decades,chaotic systems have been extensively used in cryptography because of the inherent properties like unpredictability, aperiodicity, complexity and can generate pseudo-random sequences rapidly.Therefore, image encryption algorithms based on chaotic systems have been continuously proposed and improved.[4-21]Compared with high dimensional chaotic system, a one-dimensional (1D) chaotic map is easier to implement and widely used to develop image encryption pursuing high encryption speed.For example,in Ref.[7], the technology of total shuffling was used to develop a linear-nonlinear-linear structure which was then applied in producing permutation position matrix and the diffusion matrix involved in image encryption.In 2014, Zhou[8]combined with two existing 1D chaotic maps (seed maps) to construct a new chaotic system with more complex chaotic behaviors.Then four rounds of encryption are performed to enhance the robustness and security against various attacks.For most image encryption algorithms, the encryption operation is performed in spatial domains combining diverse technologies such as deoxyribonucleic acid(DNA)coding,[9-13]elliptic curve,[14-16]quantum theory,[17,18]neural network,[19]and so on.DNA computing is widely used in image encryption due to its advantages such as enormous parallelism, high information density, and low power consumption.In Ref.[11],Wuet al.presented a content-aware module to design a DNA computing system that can be employed to permute and diffuse the encoded medical image.Compared to RSA encryption, elliptic curve cryptography (ECC) which can mitigate the performance overhead in computation processes, is especially suitable for applications in scenarios with constrained device resources.With the application of ECC,Sasikaladeviet al.[14]introduced a hybrid multilayered hyper-chaotic hyperelliptic curve to encrypt image losslessly.DNA bit scrambling was applied in original image during hyper chaotic encoding process and then the curve function was used to obtain valid points to diffuse the image.Quantum walk, a random walk model based on quantum mechanics,has good randomization and unpredictability,which enables its application in cryptography.In 2022,a controlled alternated quantum walks scheme was proposed by Gaoet al.[18]to construct substitution boxes.Three-quarters of the image which was scrambled by the quantum Arnold block transform were divided into 32 blocks substituted with different S-boxes.Memristor has unique memory function and is utilized as an artificial nerve synapse.In Ref.[19], a memristive Hopfield neural network (HNN) processing complex dynamical behaviors was proposed by Laiet al.and applied to image encryption.
Image encryption based on transform domains is another research direction and have been studied by many researchers.[22-28]For example, in Ref.[22], an XOR operation is performed between the DNA matrix transformed by the plain image and a random phase mask, and then employing the fractional Fourier transform three times in the substituted image before further encryption.To minimize the transmission load, a two-dimensional (2D) discrete cosine Stockwell transform was utilized to compress the image.[23]Then DNA-level modulus diffusion was performed on the compressed image to gain confusion and diffusion effects simultaneously.Wavelet transform is a mathematical tool for image decomposition.In some image encryption schemes based on wavelet transform, the image in spatial domain was firstly converted to wavelet domain and then undergone further processing and encryption operations.For example, the wavelet transform is used to sparsify the image before compression sensing.[29-32]In Ref.[31],after wavelet transform and compression sensing, the original image was compressed into a smaller size image that was encrypted using confusing and singular value decomposition, which harvested the less time complexity compared to other techniques.In some other image encryption schemes,encryption operations are performed directly in wavelet domain.[33-35]Since the low-frequency coefficients contain most of the information of the oringin image,while the high-frequency coefficients contain more details,to obtain higher encryption efficiency, some sub-bands are selected to encrypt.In Ref.[33], a plaintext was decomposed into four sub-bands by discrete wavelet transform.According to their weights,the low-frequency image was confused firstly and then four sub-bands was encrypted under the feedback from the confused low-frequency image.This scheme uses dynamic keys generated by message-digest algorithm 5 that uses plaintext image as input.It means that the keys needed to be transmitted to receiver when encrypting a new image,which reduces the value of application.In Ref.[34],only the low-low frequecy component decomposed by two level discrete wavelet transform was shuffled and diffused only one round.The author claims that the proposed scheme have high plaintext sensitivity but the analysis results are difficult to support the conclusion.
For the fact that, the statistical properties of every subbands in the wavelet domain of a random information source follow Gaussian distribution.In this research, a new image encryption structure was proposed according to the statistical characteristics.A brief summary of the overall contribution of the work is as follows:
(i) An improved sine map was designed and extensively tested to possess a larger chaotic region,more complex chaotic behavior and greater unpredictability.
(ii) Different from existing spatial-domain and waveletdomain image encryption systems,according to the statistical properties of a true random information source in wavelet domain, a noval encryption framework based on ISM was proposed.
(iii) Complete simulations and theoretical analysis were conducted to demonstrate the high speed and the remarkable effectiveness of WDLIC.
The remainder of this paper is as follows: an introduction to the discrete wavelet transform(DWT)and statistical properties of a true random information source in wavelet domain are presented in Section 2.Section 3 presents the improved sine map.Section 4 gives a complete description of the lightweight symmetric image cryptosystem in wavelet domain.Section 5 delivers the simulation and security analysis results of the algorithm.Eventually,we draw a conclusion in Section 6.
2.Related work
2.1.Discrete wavelet transform
DWT can be used to decompose an image into four sub-bands, namely high-frequency-high-frequency (HH),high-frequency-low-frequency (HL), low-frequency-highfrequency(LH),and low-frequency-low-frequency(LL)as illustrated in Fig.1.Figure 2 shows the one level decomposition of Lena.Most of the image energy is concentrated in the lowfrequency band and the three high-frequency bands depict the image details in horizontal, vertical and diagonal directions respectively.So in this research,the low-frequency band was chosen as the cryptographic object.

Fig.2.One level wavelet decomposition of Lena.
The detailed processing of the Haar wavelet transform for an image is as follows:[33]
wherep(x,y),p(x,y+1),p(x+1,y),andp(x+1,y+1)are four neighboring pixels in the original image.
2.2.Statistical properties in wavelet domain
For a random image, the occurrence probability of each gray level is 1/256.According to Eq.(1), becausepfollows a uniform distributionx~U(256) whereP(x=i)=1/256(i=0,1,2,...,255),LL approximately matches the Gaussian distributionx~N(255,5.4613×103) and other three subbands followx~N(0,5.4613×103),which are demonstrated in Fig.3.
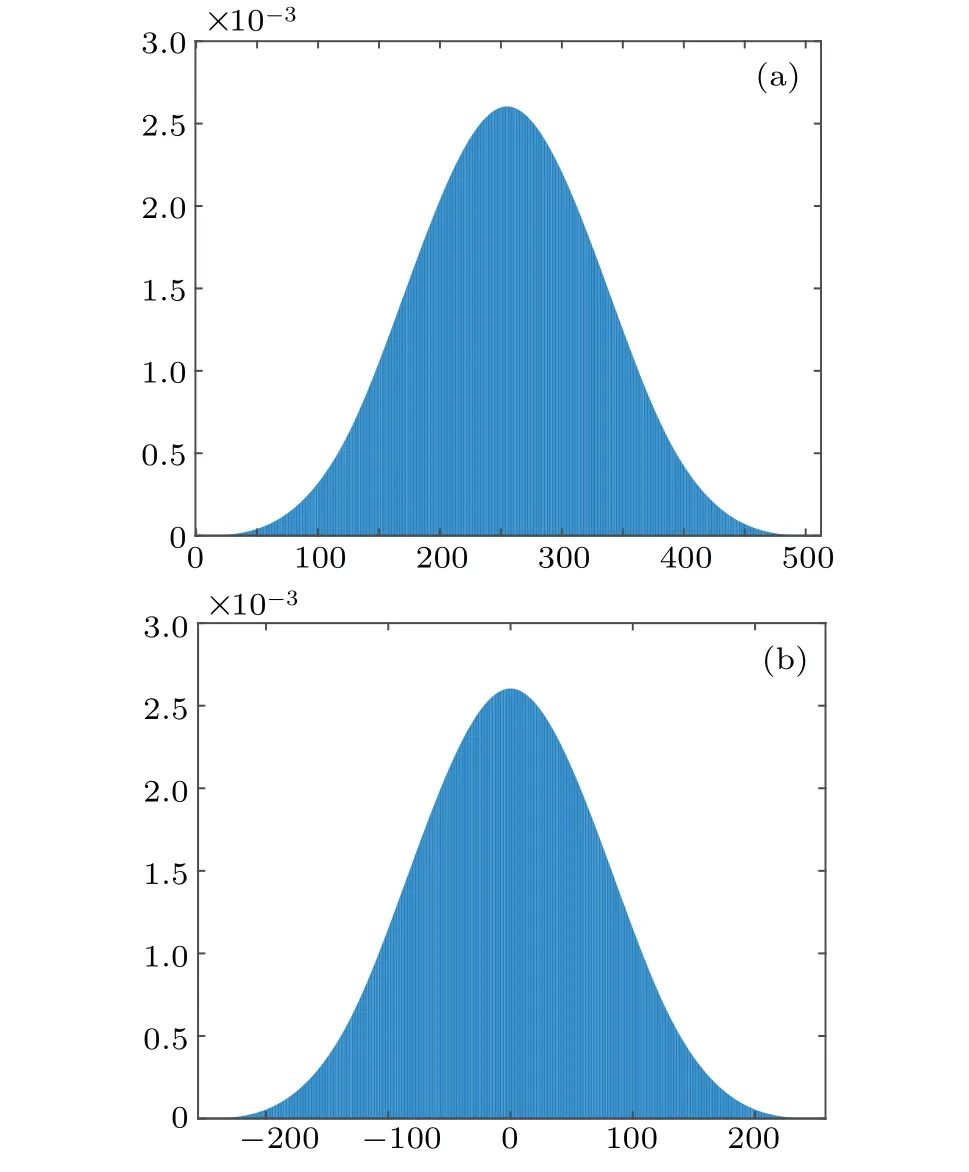
Fig.3.Statistical properties of(a)LL,(b)HH,HL,and LH.
3.Improved sine map
Sine map is a well-known 1D chaos map and can be represented by

whereris a control parameter.
In order to verify its chaotic performance, Lyapunov exponent test,bifurcation analysis,sample entropy,0-1 test,and NIST test are performed in the following subsections.
3.1.Lyapunov exponent test
Lyapunov exponent(LE)characterizes the average exponential rate of convergence or divergence between neighboring orbits of the system in phase space and is given by
wherenis the size of the generated time seriesf(xn).
A positive value of LE indicates that in the phase space,a small initial distance between the two trajectories will increase exponentially with the evolution of time.A comparative analysis of ISM and other chaotic maps including logistic-sinecosine,[36]1-DFCS,[37]1-DSP,[38]and sine map is given and its result is shown in Fig.4.We can observe that the proposed ISM map has larger LE values over a larger parameter range than other recently proposed chaotic systems.In order to visually assess the sensitivity of ISM to the initial values and control parameters,figure 5 plots the output chaotic sequences generated with different initial values or control parameters.
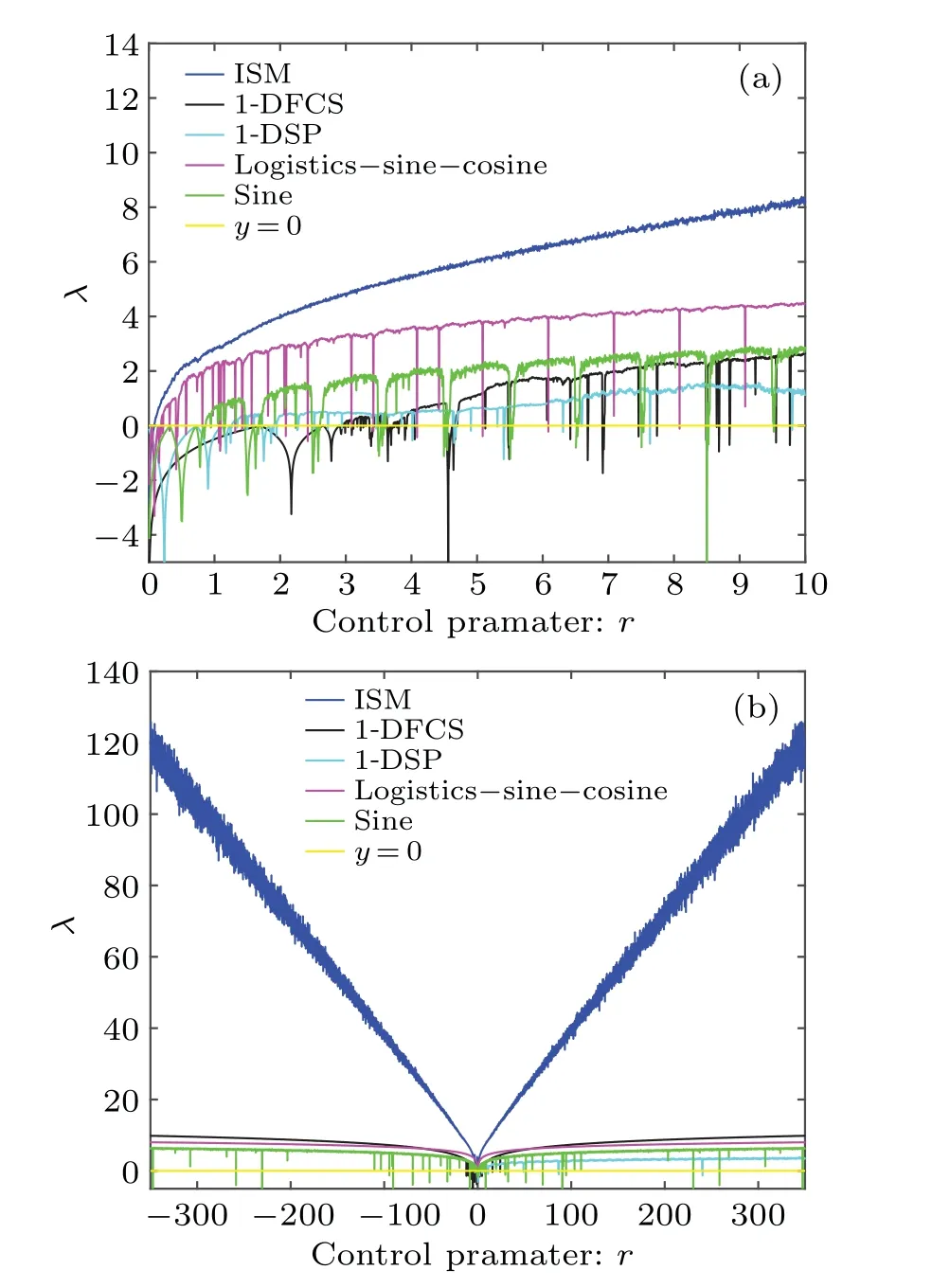
Fig.4.Lyapunov exponent of different chaotic maps.

Fig.5.Initial value and pramater sensitivity of ISM.
3.2.Bifurcation analysis
The period-doubling bifurcation path is one of the common paths to chaos.Figure 6 shows the bifurcation diagrams of ISM, logistic-sine-cosine, 1-DFCS,1-DSP,and sine map.Relative to other chaotic mappings, the bifurcation diagram exhibits that ISM possesses a much larger chaotic range.
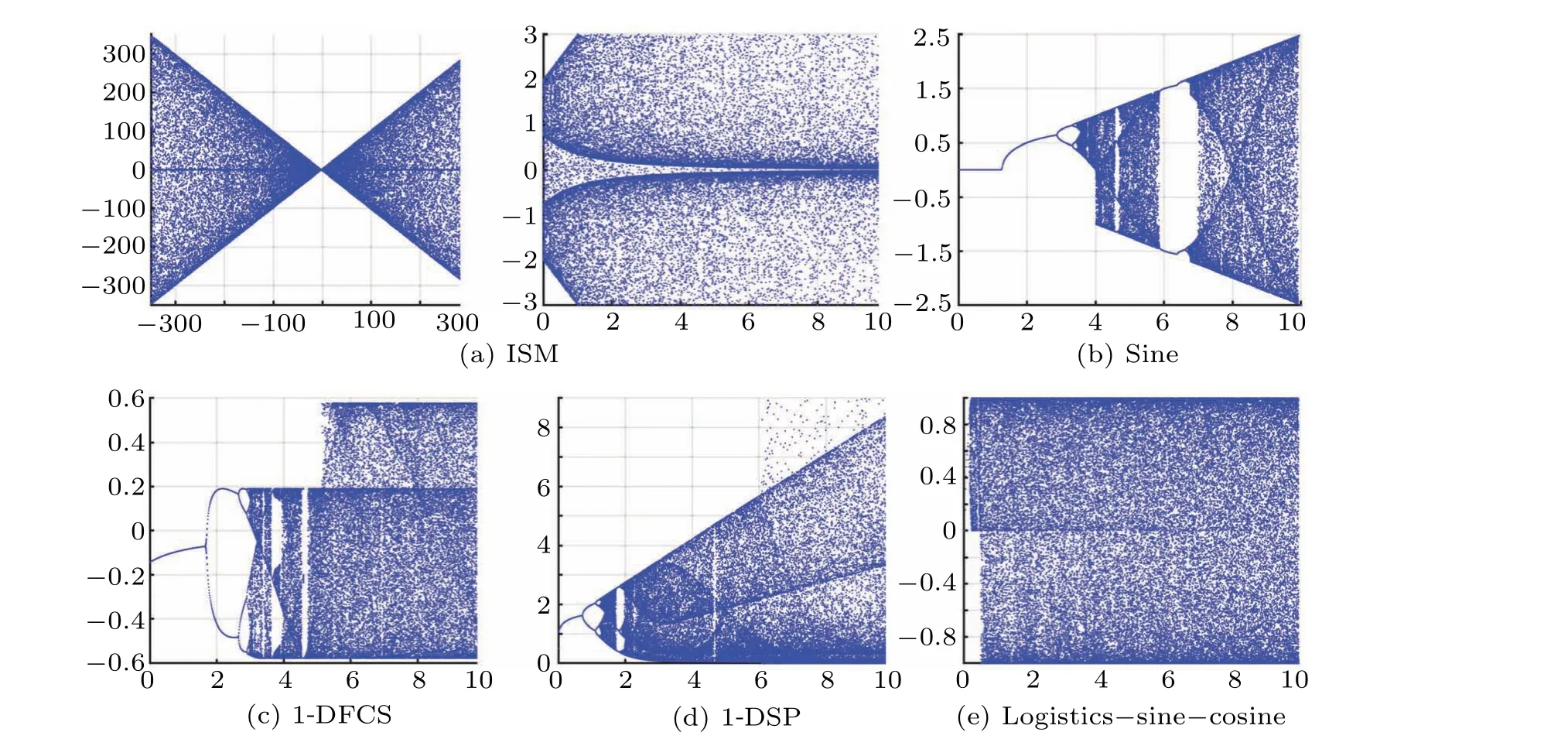
Fig.6.Bifurcation diagram.
3.3.Sample entropy
The regularity of the time series generated by dynamic systems can be measured by sample entropy (SampEn).[39]A larger SampEn value indicates less self-similarity of the time series, which means the dynamic system has a higher complexity.In Eq.(5), the template vectorDm(i) with a length ofmis taken from the time series{X(i),X(i+1),...,X(i+m-1)}.The SampEn of the time seriesXis calculated in Eq.(6).
whererdenotes tolerance.AandBare the total numbers of vectors satisfying the conditionsd[Xm+1(i),Xm+1(j)]<randd[Xm(i),Xm(j)]<rrespectively.d[Xm(i),Xm(j)]is the Chebyshev distance betweenX(i) andX(i+m-1).In our test,mandrare set to 2 and 0.2×std.The results of SampEn comparison experiments are shown in Fig.7 which demonstrates that the time series generated by ISM has higher randomness.

Fig.7.SampEn comparative experiment.
3.4.The 0–1 test
The 0-1 test can be used to determines the presence of chaos in a dynamical system by calculating the linear growth rateKcof the discrete data transformation variables and defined by
whereXis a time series with the size ofNand is generated by ISM.The constantris set to 2.If the output results close to 1,the dynamical system exists chaotic behaviors.The test results of the four different mappings are illustrated in Fig.8.The test result of ISM is close to 1 whenr ∈(-350,350).Therefore,we can conclude that ISM has better chaotic properties compared to the other four 1D chaotic maps.

Fig.8.The 0-1 test.
3.5.NIST SP 800-22 test
SP 800-22 developed by the National Institute of Standards and Technology (NIST) was utilized to validate therandomness of the sequences generated by ISM.[40]SP 800-22 consists of 15 subtests and uses a set of binary sequences as input.Then each subtest result,namelyP-values serves as a measure of randomness of the system.In our test,ISM generates a total of 1.25×105bit binary numbers as input and all the test results fall into (0.01,1) as shown in Table 1, which proves that the sequences generated by ISM iterations boast a higher degree of randomness and are suitable for image encryption.

Table 1.NIST SP 800-22 test of ISM.
4.The proposed image cryptosystem
In this section,we construct a lightweight symmetric image encryption cryptosystem in wavelet domain.Figure 9 depicts the encryption and decryption flowchart of our proposed cryptosystem.
In the following, we describe the proposed encryption cryptosystem in details:
Step 1 Alice’s fingerprint image Fin is fed into SHA-256 to generate a 256-bit hash valuefwhich is used as the secret key.
Step 2 The plaintextPwith the size ofM×Nis used as input to SHA-512 hash function to produce a 512-bit binary numberh.fandhare first processed by Eq.(11).
wherei=1,2,...,32 and the function bin2dec can convert binary numbers to decimal numbers.
Then in Eq.(12),pairwise XOR operations are performed onR1,R2, andRto obtainHwhich is used to generate two plaintext-related parameter arraysh1andh2.h1andh2are subsequently used to generate the random image and use in diffusion process.

It is worth noting that the formerN0elements are discarded.In Eq.(15),y1andz1are used to preprocess the random sequencexto obtain a new sequenceX
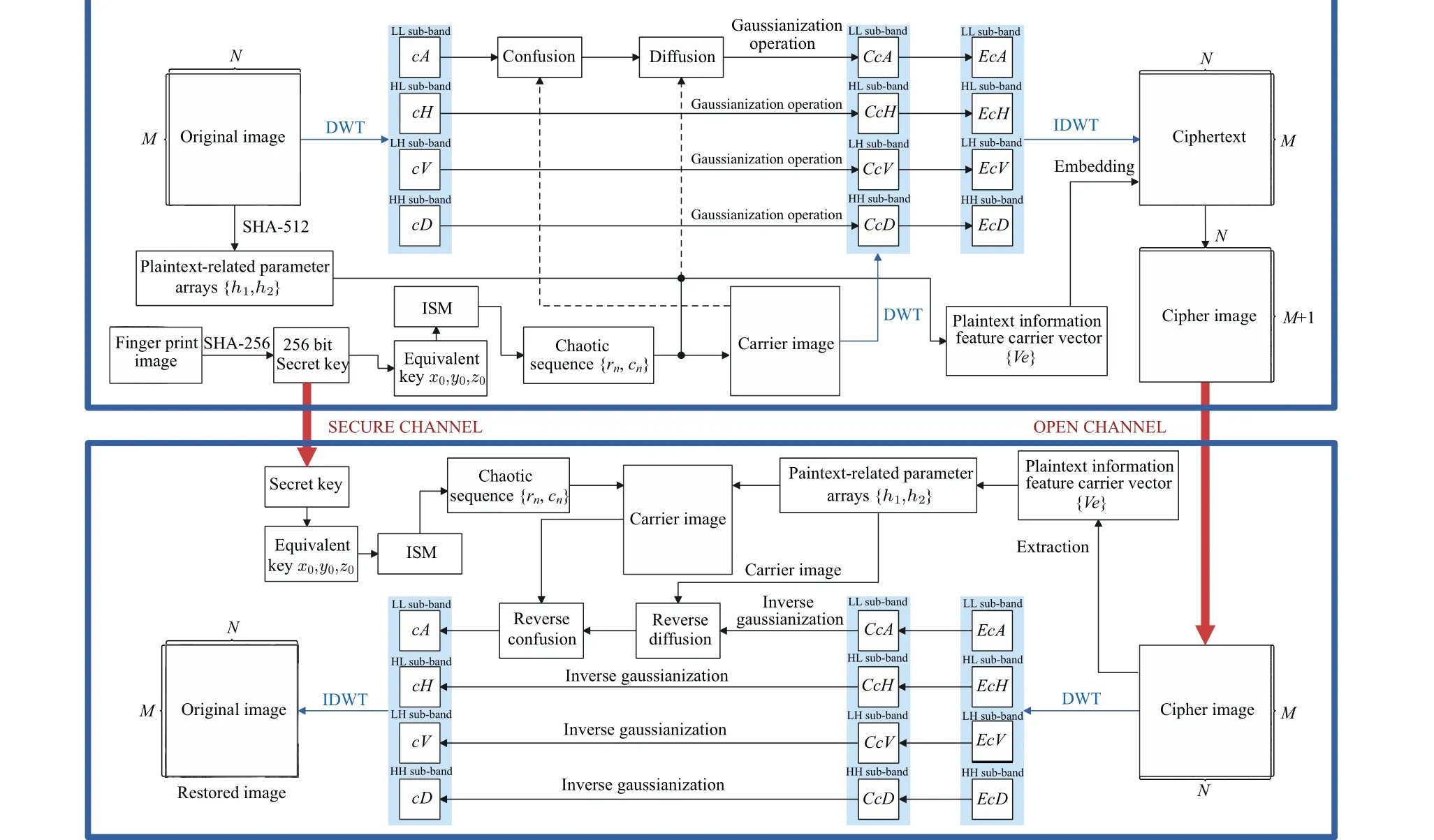
Fig.9.The proposed image cryptosystem.
And then two 1D arraysrn,cnwith the length ofMandNrespectively are obtained by the following operation:
Step 4 The vectorsh1,h2,rn,andcnare utilized to generate a random imagePcwith the same size of the plaintext image by
Step 5 DWT is performed on the plaintext imagePand the random imagePcto obtain their corresponding four sub-bands, which is expressed as Eq.(18).Four subbandscA,cH,cV,andcDcorrespond to low-frequency-lowfrequency (LL), high-frequency-low-frequency (HL), lowfrequency-high-frequency (LH), and high-frequency-highfrequency(HH)respectively.
[cA,cH,cV,cD]=dwt2(P,′haar′),
And then converts the coefficients’values of HL,LH,and HH into positive ones as
Step 6 Because the low frequency component contains the basic information of the image,thecAis chosen to encrypt in our work.Two random sequencesSC1andSC2with the size ofM/2 andN/2 respectively are generated usingPcby applying Eq.(20).SC1andSC2are utilized to permutecAto obtaincA′which is then transformed into a one-dimensional vector.
Step 7 Performing the diffusion oncA′to obtain a vectorEncAwhich is then reshaped to a matrix with the size ofM/2×N/2.The complete encryption process is detailed in Algorithm 1.

Algorithm 1 Encryption algorithm Input: A sub-band of plaintext image cA and its size (M/2,N/2), two random sequences SC1 and SC2, two plaintext correlation parameter arrays h1 and h2,an empty vector temp.Output: Encrypted sub-band of plaintext image EncA.1: for i=1:M/2 2: temp=cA(i,:)3: cA(i,:)=cA(SC1(i),:)4: cA(SC1(i),:)=temp 5: end for 6: for i=1:N/2 do 7: temp=cA(:,i)8: cA(:,i)=cA(:,SC2(i))9: cA(:,SC2(i))=temp 10: end for 11: cA′=reshape(cA,[1,M/2×N/2])12: for i=1:M/2×N/2 do 13: En cA(i)=mod(mod(cA′(i)+h1(mod(i,8)+1)×h2(mod(i,8)+1)×107,512),512)14: end for 15: En cA=reshape(En cA,[M/2,N/2])
Step 8 According to the statistical properties in the wavelet domain discussed in Section 2, the distributions of sub-bands of the ciphertext should be as close as possible to the ones in a random image.The complete Gaussianization process is detailed in Algorithm 2.

Algorithm 2 Gaussianization of sub-bands Input:The encrypted sub-band En cA,three sub-bands of plaintext image cH,cV,cD,four sub-bands of random image CcA,CcH,CcV,CcD.Output: Four sub-bands of ciphertext EcA,EcH,EcV,EcD 1: for i=1:M/2 2: for j=1:N/2 do 3: EcA(i,j)=mod((En 1000 ),512)4: EcH(i,j)=mod((cH(i,j)+999×CcH(i,j)cA(i,j)+999×CcA(i,j)1000 ),512)-256 5: EcV(i,j)=mod((cV(i,j)+999×CcV(i,j)1000 ),512)-256 6: EcD(i,j)=mod((cD(i,j)+999×CcD(i,j)1000 ),512)-256 7: end for 8: end for
Step 9 Perform inverse discrete wavelet transformation on the four sub-bandsEcA,EcH,EcV,EcDto obtain cipher imageE.
Step 10 In Eqs.(21)and(22),we construct the plaintext information feature carrier vectorVeand the position vectorIn1using the random arraycn.

On the receiving end, the same secret keys are utilized to iterated ISM to generate the same random sequencesrn,cnfirstly.Then the plaintext information feature carrier vectorVeus extracted from the cipher image and the plaintextrelated parameter arraysh1,h2are obtained.After that,using Eq.(15),h1andh2are used for the random imagePcgeneration.Finally,the decryption process detailed in Algorithm 3 is performed to obtain the decrypted image.

Algorithm 3 Decryption algorithm Input: Four sub-bands of cipher image EcA,EcH,EcV,EcD,sub-bands of random image CcA,CcH,CcV,CcD, two random sequences SC1 and SC2,two plaintext correlation parameter arrays h1 and h2,an empty vector temp.Output: The decrypted image D.1: for i=1:M/2 2: for j=1:N/2 3: En cA(i,j)=mod(EcA(i,j)-999×CcA(i,j)+512,512)×1000 4: cH(i,j)=mod(EcH(i,j)-999×CcH(i,j)+768,512)×1000 5: cV(i,j)=mod(EcV(i,j)-999×CcV(i,j)+768,512)×1000 6: cD(i,j)=mod(EcD(i,j)-999×CcD(i,j)+768,512)×1000 7: end for 8: end for 9: En cA,[1,M/2×N/2])10: for i=1:M/2×N/2 11: cA′(i) = mod(En cA=reshape(En cA(i)-h1(mod(i,8)+1)×h2(mod(i,8)+1)×107,512)12: end for 13: cA=reshape(cA′,[M/2,N/2])14: for i=M/2:-1:1 15: temp=cA(i,:)16: cA(i,:)=cA(SC1(i),:)17: cA(SC1(i),:)=temp 18: end for 19: for i=N/2:-1:1 20: temp=cA(:,i)21: cA(:,i)=cA(:,SC2(i))22: cA(:,SC2(i))=temp 23: end for 24: D=idwt(cA,cH-256,cV-256,cD-256,′haar′)
5.Experimental simulation results and security analysis
Aiming to evaluate the performance of WDLIC, in this section various simulations are performed on Matlab 2022a.The experiments are conducted on a personal computer with Core(TM)i7-11800H CPU 2.30 GHz,16 GB RAM and Windows 10 operating system.
5.1.Key space
Key space means the total number of keys that a cryptosystem can select.It is generally accepted that a cryptosystem can resist brute-force attacks when the key space is greater than 2100.In this paper, Alice’s fingerprint image was utilized to generate three keysx0,y0, andz0via SHA-256.If the computer accuracy is 1015,we can calculate the key space=(1015)3>2149.Therefore,the key space of WDLIC is large enough to invalidate brute-force attacks.
5.2.Histogram analysis
The histogram of an image reflects the distribution of pixels.In spatial domain, the more uniform of an encrypted image’s histogram, the more challenging it is for an attacker to extract meaningful information from it.In wavelet domain,the distributions of sub-bands of the ciphertext should be as close as possible to Gaussian distribution.We tested the histograms of Lena and other five images with the size of 512×512 before and after decryption.As shown in Figs.10 and 11, the WDLIC can resist the statistical attacks well.

Fig.10.Histogram.(a) Lena; (b) histogram of Lena; (c) histograms of four ciphertext sub-bands;(d)cipher image;(e)histogram of cipher image.

Fig.11.Simulation results of five images,1-Peppers,2-Barbara,3-Baboon,4-Boat,5-Girl.(a)Five plain images;(b)bistograms of five plain images;(c)five cipher images;(d)histograms of five cipher images.
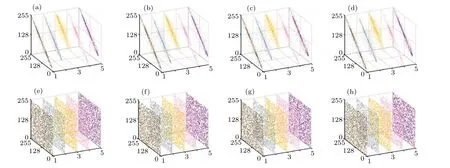
Fig.11.Correlation analysis of five images, 1-Peppers, 2-Barbara, 3-Baboon, 4-Boat, 5-Girl: the first line is the correlation analysis of five images in four specified directions,(a)vertical;(b)horizontal;(c)diagonal;(d)anti-diagonal.The secord line is the correlation analysis of five cipher images in four specified directions.
5.3.Correlation analysis
Exploiting high correlation of neighboring pixels to attack encryption algorithms is a common tactic for attackers.A secure encryption algorithm should eliminate the correlations of images.The correlations between two adjacent pixels in four specified directions can be measured by the correlation coefficients(cc).The fomula of cc is given as
whereNis the number of pixels arbitrarily selecting from the image.xandyare two neighboring pixels.Figure 12 shows the correlation analysis in four specified directions and the results of correlation coefficients analysis are shown in Tables 2 and 3,which indicates that WDLIC is effective in eliminating the strong correlation.

Table 2.The results of correlations analysis.

Table 3.The comparative correlation coefficients analysis of encrypted Lena.
5.4.Information entropy
Information entropy reflects the uncertainty of an information source.For a 256-grey level image,the ideal information entropy of the cipher image should be as close as possible to 8.The mathematical formula of the information entropy is
wherep(mi)is the probability of the appearance of the pixelmiand 2Nrepresents the total number ofmi.As seen in Table 4,all the simulation results are extremely close to the desired value, which indicates that WDLIC can completely confuse the image information.
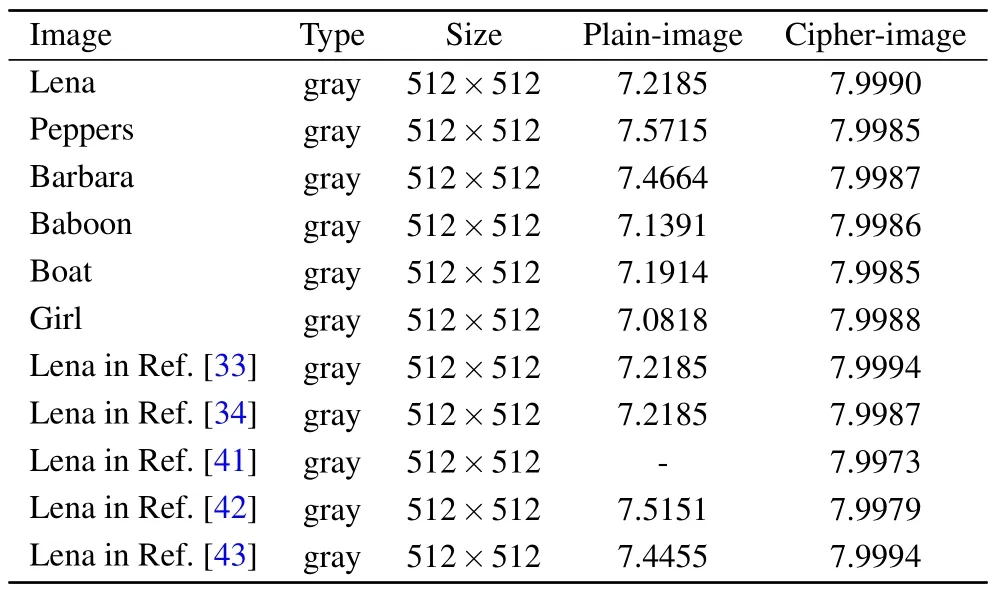
Table 4.Information entropy analysis results.
5.5.Sensitivity analysis
A superior encryption algorithm should have strong key sensitivity and plaintext sensitivity to defend against differential attacks and chosen plaintext attacks.In general,the number of pixels changing rate (NPCR) and the unified average changed intensity(UACI)are exploited to to evaluate the sensitivity.Mathematically,NPCR and UACI are calculated by

5.5.1.Key sensitivity
In our work, the secret key generated from Alice’s fingerprint image is used to produce the initial values of ISM.A subtle change in the key can result in a significant difference in the cipher image.Take standard image Lena as an example, figure 13 illustrates the decrypt results with the correct and wrong key.And Table 5 lists the corresponding NPCR and UACI test results.One can see that the encryption and decryption process of WDLIC are very sensitive to the key.

Fig.13.Visualization tests for key sensitivity.(a)The encrypted image with the security key key1=[N0,x0,y0,z0];(b)the decrypted image using correct key; (c) the decrypted image using key1 =[N0,x0,y0,z0]; (d) the decrypted image using key2=[N0+1,x0,y0,z0];(e)the decrypted image using key3=[N0,x0+10-15,y0,z0]; (f) the decrypted image using key4 = [N0,x0,y0+10-15,z0];(g)the decrypted image using key5=[N0,x0,y0,z0+10-15].
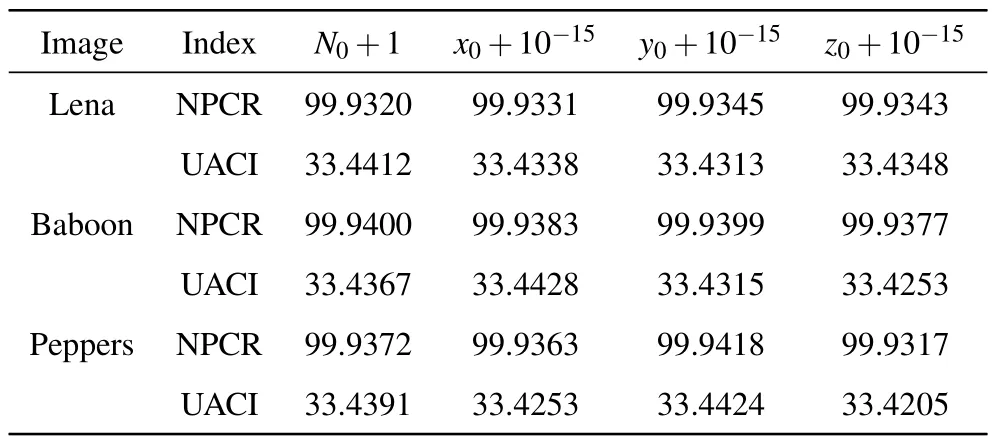
Table 5.NPCR and UACI performance of key sensitivity analysis.
5.5.2.Plaintext sensitivity
Plaintext sensitivity analysis seeks to determine whether a slight change of plaintext will have a significant impact on ciphertext.Table 6 lists the average UACI and NPCR analysis results of WDLIC and other algorithms.The results of the study reveal that WDLIC exhibits robustness against differential attacks and chosen plaintext attack.

Table 6.NPCR and UACI performance of plaintext sensitivity analysis.
5.6.Running time efficiency analysis
The speed of encryption is an important indicator for cryptosystem, especially for some application scenarios with limited resource or need real-time encryption.In our work,we select some standard images with the size of 256×256 and 512×512 as the test images.Table 7 lists the running time of different algorithms in MATLAB programming environment.Obviously,the proposed WDLIC achieves a significant advantage in terms of speed.

Table 7.Time consumption comparisons with other methods(in seconds).
5.7.Noise attack and data loss
A strong cryptosystem should have the robustness of noise attack and data loss.In this subsection, as shown in Fig.14, the cipher image is added with different intensities salt-and-pepper noise or malicious cut.One can see that the decrypted image contains most visual information of original image.Peak signal to noise ratio (PSNR) is used to evaluate the decrypted image quality and the results shown in Table 8 prove that WDLIC has strong robustness to resist noise attack and data loss.

Fig.14.Results of noise resistance and data loss.(a) The encrypted images contaminated by salt-and-pepper noise 1% density; (b) the encrypted images contaminated by salt-and-pepper noise 5% density; (c) the encrypted images contaminated by salt-and-pepper noise 10%density; panels (e)-(g) are the corresponding decrypted images.Panel (d) is the encrypted Lena with 50×50 data loss and panel (h) is the decrypted image of panel(d).

Table 8.Noise attack analysis using PSNR indicator.
6.Conclusion
This paper introduces an improved sine map.Extensive tests including Lyapunov exponent test, bifurcation analysis,sample entropy, the 0-1 test and NIST test indicate that ISM possesses a larger chaotic region, more complex chaotic behavior and greater unpredictability compared to the previous chaotic maps.Building upon ISM, we propose a lightweight image cryptosystem wherein only the low-frequency-lowfrequency component is chosen to encrypt and then Gaussianization is employed across all sub-bands.Experimental simulation results and security analysis demonstrate that WDLIC achieves satisfactory security, encryption speed and robustness against various attacks.The robustness against noise and data loss of WDLIC is compromised due to the selective encryption employed.In the future, our efforts will focus on optimizing the selective encryption strategy to overcome the limitations and utilizing WDLIC to develop potential applications for multimedia data encryption like color images and even video on hardware.
Acknowledgements
Project supported by the Key Area Research and Development Program of Guangdong Province, China (Grant No.2022B0701180001), the National Natural Science Foundation of China (Grant No.61801127), the Science Technology Planning Project of Guangdong Province, China(Grant Nos.2019B010140002 and 2020B111110002), and the Guangdong-Hong Kong-Macao Joint Innovation Field Project(Grant No.2021A0505080006).
- Chinese Physics B的其它文章
- A multilayer network diffusion-based model for reviewer recommendation
- Speed limit effect during lane change in a two-lane lattice model under V2X environment
- Dynamics of information diffusion and disease transmission in time-varying multiplex networks with asymmetric activity levels
- Modeling the performance of perovskite solar cells with inserting porous insulating alumina nanoplates
- Logical stochastic resonance in a cross-bifurcation non-smooth system
- Experimental investigation of omnidirectional multiphysics bilayer invisibility cloak with anisotropic geometry

