Does the Hartman effect exist in triangular barriers
Qing-Ling Li(李青玲), Shuang Zheng(郑爽), and Zhi Xiao(肖智),2,†
1Department of Mathematics and Physics,North China Electric Power University,Beijing 102206,China
2Hebei Key Laboratory of Physics and Energy Technology,North China Electric Power University,Baoding 071000,China
Keywords: triangular barrier,Hartman effect
1.Introduction
As a purely quantum mechanical phenomenon, quantum tunneling is extremely important in a vast range of fields,such as helping overcome the Coulomb barrier in nuclear fusion,[1]tunneling-induced DNA mutation,[2]scanning tunneling microscopes,advanced electronics like tunnel diodes[3]and even false vacuum decay[4,5]in cosmology.With the extensive exploration of quantum tunneling, an early discovered time issue[6,7]is still unresolved; namely, how long does it take for a tunneling particle to traverse a barrier region.Recently,this matter again returned as a bone of contention among researchers,[8-13]mainly thanks to the ultraprecise timing technology developed in attosecond science.[14,15]There are various definitions of tunneling time in the literature, such as Esenbud-Wigner time delay (also termed phase time),[16-18]dwell time[19]and Larmor time.[20-22]Each of them reflects quite distinctive features in quantum tunneling.[23]Aside from the well-studied tunneling times mentioned above, several other time definitions have been proposed.These include the tunneling flight time[10,11]introduced by Rivlinet al.,the selfadjoint time operator introduced in analogy with the relativistic Dirac Hamiltonian[24]and the entropic time inspired by the statistical implication from the relation between the imaginary B¨uttiker-Landauer time and the inverse temperature.[25]
With the push from the rapid progress in attosecond science,[26]the question of whether quantum tunneling takes a finite time or is instantaneous seems closer to be answered.Even if it is acknowledged that tunneling takes a finite time,a well-accepted time definition in the academic community
is still lacking.For example, phase time keeps track of the peak of a moving wave packet while a thick barrier behaves as a high energy filter,which makes the track of the peak of a wave packet meaningless since it is highly distorted after tunneling;dwell time measures the ratio of the expectation value of a projection operator∫xfxidx|x〉〈x| (the barrier region is included in [xi,xf]) to the incident flux but never distinguishes transmitted waves from reflective partial ones.Many other time definitions, such as Pollack-Miller time[27]or B¨uttiker-Landauer time,[28]also suffer from various drawbacks, such as the failure to fulfillτDW=τT|T|2+τR|ℛ|2.In contrast,Larmor time, which maps the time evolution to the rotation angle swept by the spin of an incoming particle in the“clock face” orthogonal to the magnetic field coving the barrier, is not only experimentally feasible[8,9]but also closely related to weak measurement.[29,30]Thus its out-of-plane part corresponds to the back reaction of a measurement.[31,32]Interestingly,the four times can be classified either as the dwell time a particle sojourning in the barrier or the passage time a particle getting across it,and they are neatly unified with the path integral formalisms.[23]These treatments may support that tunneling time can be best viewed as a distribution and thus different definitions only capture specific features of the distribution.In this paper, we mainly focus on the first three well-posed tunneling times and the Larmor time in particular.
As a paradigm in the study of tunneling time, the rectangular barrier draws the most attention and has been analyzed extensively,[33]especially in the discovery of the Hartman effect.[6,7,34]It is proposed that the superluminal behavior arising from the lack of independence of tunneling time on the barrier width is an artifact of the misinterpretation[35,36]of phase time as traversal time.[37]This viewpoint receives support from the study of phase and dwell times in a rectangular double barrier and its deformation,double-δbarrier.[38]Later,an analytical study on smoothAsech2[x/a] barriers showed that a smooth rather than vertical scattering interface indeed alleviates or even smears out the time saturation effect with the increase of barrier width, which is proportional toa, largely due to the steep rising of tunneling rate in a very narrow region in momentum space.[39]Recently,the sech2-type barrier and well were thoroughly studied in exploring the detail of the reshaping mechanism and the causality issue by analyzing the pole structure of transmission amplitude.[40]Utilizing generalized phase time with time reversal invariance,the Hartman effect in an arbitrary shape with smooth barriers has been studied.[41]A natural example of smooth barriers is the linear gravitational potential, which was first studied by Davies when exploring whether the weak equivalence principle holds in the quantum domain.[42,43]Later on, we proposed a new configuration of magnetic field,spin and momentum of a tunneling particle through the linear potential when analyzing the Larmor time.[44]
In this paper, we extend our previous study of tunneling times in linear potential[44,45]to exact triangular barriers(ETBs), which are barriers with vertical edges either on the left or right side and thus are natural truncations of linear barriers.The major advantage of studying triangular barriers(TBs)is that they can provide analytical solutions.Moreover, TBs have barrier width, height and two side slopes as varying parameters, and these shape parameters facilitate the study of barrier shape sensitivity for various tunneling times.As far as we know, the study of tunneling in TBs was initiated by Fowler and Nordheim to explore the mechanism of electron emission induced by intense electric fields from metals,[46,47]and it is also partially motivated as a rough simplification of the effective potentialin laser-induced tunneling ionization.[48]A recent study of the Harman effect through comparisons of tunneling in square and TBs can be found in Refs.[49,50].Here we mainly compare the phase, dwell and Larmor times for a particle tunneling through a pair of MS ETBs, namely the positive-slope exact triangular barrier(PETB)and the negative-slope exact triangular barrier(NETB).The two kinds of ETBs can be regarded as the two limiting cases of the general TBs.The study of general TBs is in progress.The present study undoubtedly demonstrates the barrier-shape sensitivity of various reflective tunneling times.By defining the velocities associated with these tunneling times, we investigate the Hartman effect further in TBs.
The rest of our paper is organized as follows.In Section 2,we present the basic solution of the Schr¨odinger equation with TBs and then we demonstrate the basic features of phase,dwell and Larmor“times”in order in Section 3.In Section 4 we define the tunneling velocities associated with phase and Larmor times, and show the barrier width dependence to illustrate the absence of a saturation effect of the tunneling time for TBs.We conclude our results in Section 5.
2.Basic theory of a TB
It is necessary to revisit the one-dimensional tunneling solutions of TBs,which may serve as a simple one-dimensional approximation to the laser-induced tunneling ionization.[14,51]For simplicity,we begin with a PETB,which can be regarded as the truncation of a linear barrier,[44]see Fig.1(a).
For a particle tunneling through a TBVtri(z)=Θ(z)Θ(Lz)az,whereaandLare the slope and width of the PETB,respectively.The general solution to the Schr¨odinger equation

where the upper or lower sign in±depends on whether the particle is injected from the left or right side, andφik(z) andφtk(z)describe the injected and transmitted waves.For a particle inside the region of a PETB,the general solution is



Fig.1.The probability density distribution |φk(z)|2 for a particle with energy (¯hk)2/(2m) tunneling through two spatial MS TBs Vtri(z) and Vtri(-z).The curves with wave numbers k=0.7,1.5,2.5 are depicted with light green,blue and red colors,respectively.
Here we explicitly write down the eigensolution for a PETB in the following and degrade the eigensolutions for the MS NETB and the more general TB in Appendix B.The ansatz for the scattering eigensolution of the PETBVtri(z)is
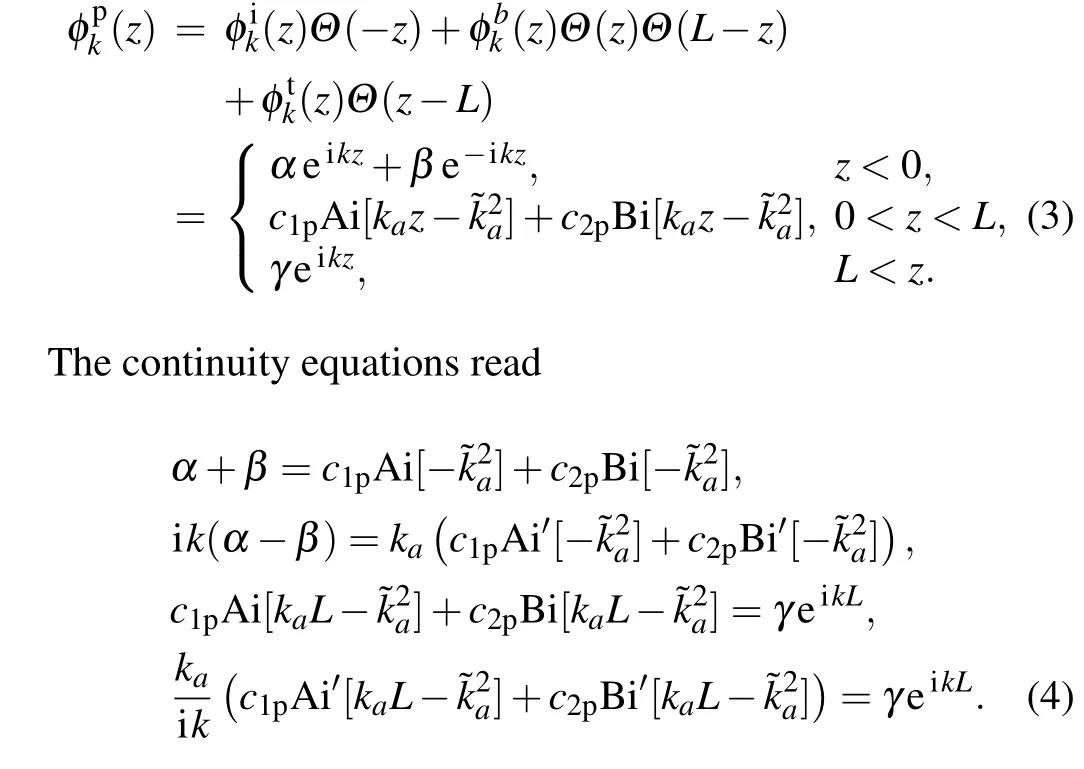
For simplicity, we set the incoming flux as a unit such thatα=1 and the coefficients can be obtained in a straightforward way as
whereRp≡β/α,Tp≡γ/αare reflective and transmitted amplitudes,respectively,and the subscript p in the coefficients above is for PETBs; similarly the subscript n is for NETBs.We have also defined the following functions:
andΩc=Ωc1+Ωc2.The functions in Eq.(9) are also useful for the eigensolution of the MS NETB,Vtri(-z), shown in Fig.1(b), see Appendix B.The relative probability density profiles for a particle scattering off a pair of MS ETBs in Fig.1 are quite different.Interestingly, the transmission amplitudes (6) and (B3) are exactly the same, i.e.,Tp=Tn;the reflection amplitudes (5) and (B2) are closely related,i.e., Den[Rp]=Den[Rn] and Num[Rp]=(Num[Rne2ikL])*,where“Den”and“Num”denote denominator and numerator,respectively,* means the complex conjugate and e-2ikLis a phase factor due to the coordinate choice.This is only a special case of a general result derived from the one-dimensional stationary Schr¨odinger equation with the potentialV(z)∈R,namely,the transmission amplitudes must be the same and the reflection amplitudes are closely related for a pair of MS barriersV(z)andV(-z),whereV(z)can be of an arbitrary shape with a finite nonzero region.[53]
3.The three kinds of tunneling time
3.1.Phase time
Phase time or Eisenbud-Wigner time[16,17,19]is a wellmotivated time definition in quantum tunneling, though it lacks essential causality relevance to correlate the transmitted and incoming wave packets and thus cannot capture the elapsed time in the tunneling process.[34]Chasing the peak of a wave packet is useless since a thick barrier works as a high-energy filter and the shape of an incoming wave packet is strongly distorted after tunneling.However,phase time is still a valuable definition in evaluating the time scales in quantum tunneling[38]and reveals the self-interference between the incoming and reflective partial waves.For example,we will see below that the reflective phase times are quite different for a pair of MS ETBs.The phase times corresponding to reflective and transmitted partial waves are defined below:
whereLis the barrier width andl0is the spatial distance ahead of the barrier, andℛandTare the reflection and transmission amplitudes,respectively,say,Eqs.(5)and(6)for a PETB.Also, note that we have ignored the multivaluedness of the tangent function.In other words, we choose the valueθS ∈[-π/2,π/2]for the inverse function of“θS=tan-1[tan(θS)]”,whereS=R,T.
Since the transmission amplitudes are the same for a pair of MS barriers,such as Eqs.(6)and(B3),the resulting transmitted phase times are also the same.In the following, we do not distinguish the two transmitted phase times(as well as the transmitted Larmor times) provided that the two barriers involved are MS.



Fig.2.The transmitted phase time delays ΔτTphase with wave number k for fixed barrier width L=3 nm and barrier height V0 ≡aL=9µV,respectively.The legends with different colors are for different barrier heights in(a)and different barrier widths in(b)and insets,respectively.The units in the vertical and horizontal axes in the insets are exactly the same as the units in the subfigures.(a) The k-spectrum of transmitted phase time delay with fixed barrier width L=3 nm.The inset illustrates the τTphase with the same L.(b)The k-spectrum of transmitted phase time delay with fixed barrier height V0=9µV.The inset illustrates the τTphase with the same V0.



Fig.3.(a)and(b)The reflective phase times e for are plotted with varying wave number k and norm of slope a by keeping the product of barrier height and width V0L=aL2=6.4×6.4µeV·nm a constant,respectively.


3.2.Dwell time
In comparison with phase time, dwell time is positively defined and averages over all scattering channels without distinguishing between reflective and transmitted partial waves.Dwell time is defined[54]as



Fig.4.(a)and(b)The dwell times and are plotted with varying wave number k and norm of slope a by keeping the barrier area A= V0L=3.2×6.4µeV·nm a constant,respectively.



3.3.Larmor times
The conventional notion of time refers to a correlation between a certain time-consuming process and the dynamical variable involved, such as the time of a sidereal day and the recording of the rotation of a pointer on a clock face, or the half-life period of the ratio of the number of decayed atoms.Similarly, we can also use some dynamic variables to record the time elapsed in tunneling phenomena.This is the underlying idea for a Larmor clock, where one utilizes the internal degree of freedom,the spin carried by a particle such as a neutron, to determine the time evolved in tunneling.The correlated“pointer”is the angle the spin sweeps on a Bloch sphere.
To make use of a Larmor clock,a small magnetic field is imposed on the region of the ETB only and the Hamiltonian becomes



Fig.6.Reflected Larmor time τ plotted with wave number k for fixed barrier width L and fixed barrier heights V0,respectively.(a)τfor fixed barrier width L=3 nm.The barrier heights in the legend from top to bottom correspond to slopes a=1.5, 2.1, 3, 4, 5.5µeV/nm, respectively.(b)τfor fixed barrier height V0 =9µeV.The different barrier widths in the legend from top to bottom correspond to slopes a=3,1.8,1.125,0.9,0.75µeV/nm,respectively.


Fig.7.Reflected Larmor time plotted with respect to wave number k for fixed barrier width L and fixed barrier heights V0,respectively.(a) τ for fixed barrier width L=3 nm.(b) τfor fixed barrier height V0=9µeV.

withs=0,1 here corresponding to the Airy functions in the upper and lower of the Pauli spinor in Eq.(21),respectively.reflected partial waves.Whenkis sufficiently small, the particle is most probably reflected and hence is dominated by the reflected partial wave;on the contrary,whenkis large enough,the scattered particle is dominated by the transmitted partial wave, so it is no surprise that dwell time gets close to either the transmitted or reflected Larmor time whenkis sufficiently large or small.This fact is shown by the coincidence of the solid curves representing dwell times with the dashed ones representing the corresponding Larmor times in Fig.8.

Fig.8.Comparison of dwell and Larmor times plotted with respect to wave number k.(a)The comparison of with τ and τ for a PETB when the barrier width L is fixed.(b) The comparison of with τand τor an NETB when the barrier height V0 is fixed.The inset magnifies the four curves of τ and τwith two different barrier widths within the region k ∈(3.5,5.5)×nm-1.

4.Saturation effect and the slope dependence of Larmor times

To reveal whether there is a barrier width saturation effect,i.e.,the well-known Hartman effect discovered in rectangular barriers,[34]it is necessary to study theLdependence explicitly.The superficial acausality of the Hartman effect relies on two premises: (1)We take it for granted that the tunneling time involved has the meaning of traversal time,[36]a semiclassical concept not necessarily applicable to quantum tunneling, which is a purely quantum mechanical phenomenon without any classical analogy.(2) The saturation of tunneling time with the increase of barrier width leads to an unlimited group velocity of tunneling particle.However, one can view the“apparent acausality”in timing tunneling as a peculiar feature of weak measurement in post-selection of the exponentially suppressed transmitted subensembles from the total ensembles,[31,32,60]and thus it is impossible to utilize tunneling to transfer information[10,11,61]superluminally.
Besides the two points mentioned above, we think that a rectangular barrier with steep edges is too special and it is

For velocities corresponding to reflective times, we have to classify the definitions into two classes.For a TB with a positive-slope left edge such as a PETB,we can define reflective Larmor velocity

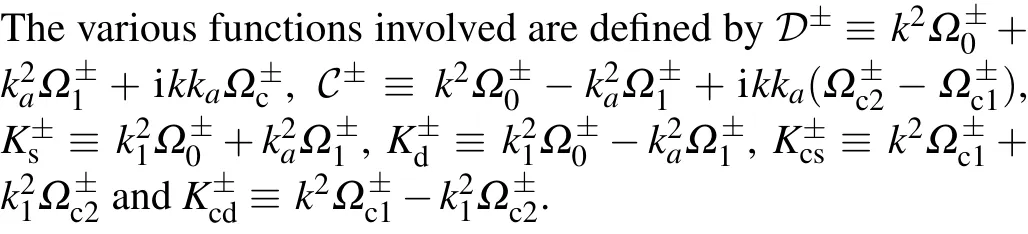
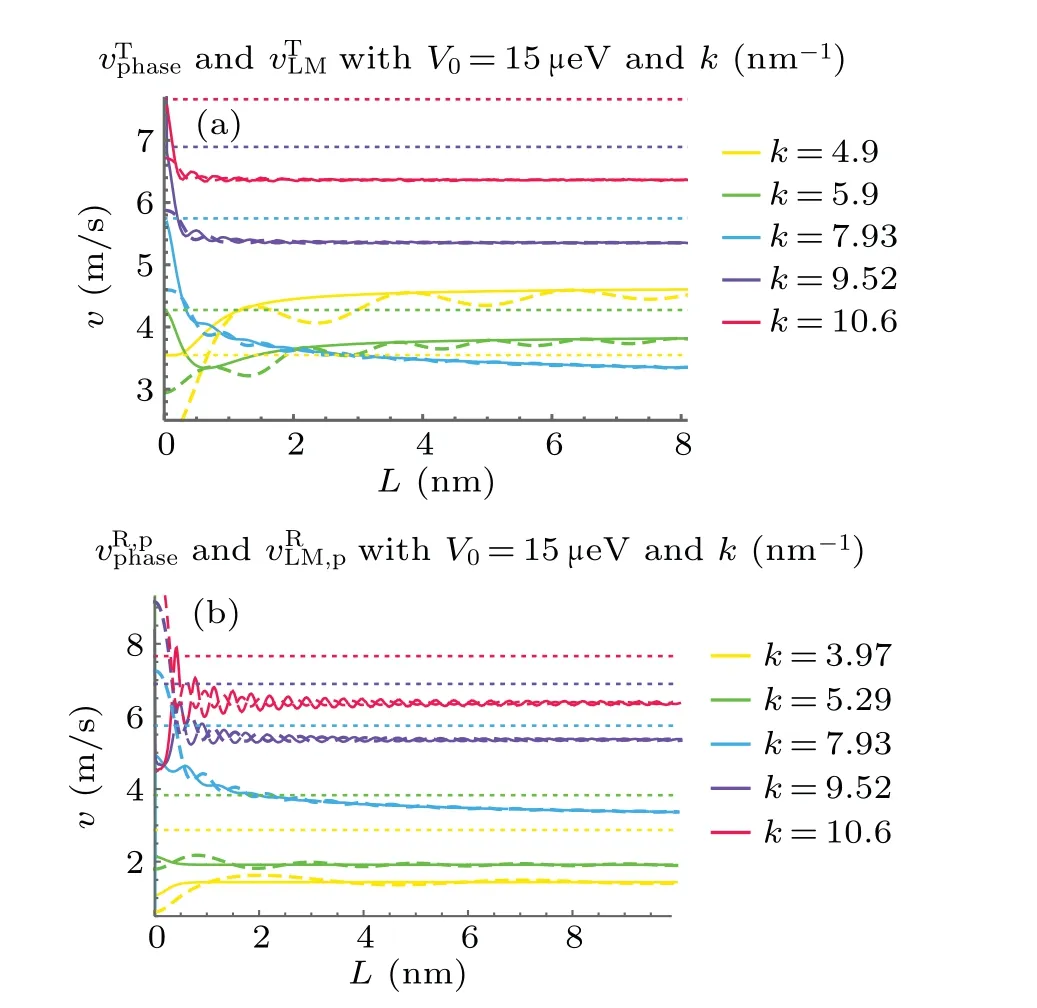
Fig.9.The barrier width dependence of the velocities defnied from the transmitted and reflected Larmor times for PETBs.The dotted lines correspond to free velocities vf and the solid and dashed curves correspond to Larmor and phase velocities, respectively.Note that k0 ≡/¯h=7.93 nm-1 represented by the blue lines or curvescorresponds to the critical wave number.(a) The vand with fixed k by varying barrier width L.(b)The v and v with fixed k by varying barrier width L.


A similar behavior can also be observed for TBs with the general shape denoted byΔl1:l2, where the subscript denotes the ratio of the widths separated by the vertical line passing the apex of the triangular barrier, see Appendix D for details.In short conclusion,for transmitted particles,a wide TB seems to accelerate particles’propagation whenkis much smaller thank0,while decelerating it whenkis closer to and larger thank0.However, the situation is the opposite for reflected particles;namely whenk <k0, the presence of a wide TB retards the reflection of the reflective particle in comparison to free one.For a TB withl1:l2>1, only whenkis significantly larger thank0does the reflected particle go quicker than a free one;while for a TB with steep left slopes, i.e.,l1:l2<1, the reflection velocity acquires a discontinuous jump whenk ≥k0.In other words, a wide TB indeed retards the propagation of the reflected particle withk <k0, see Fig.D4.The velocities of a particle scattered off a generic TB are also defined in analogy to Eqs.(24)and(25).Our discussion of TBs with a generic shape is very brief and we will leave the details for future work.
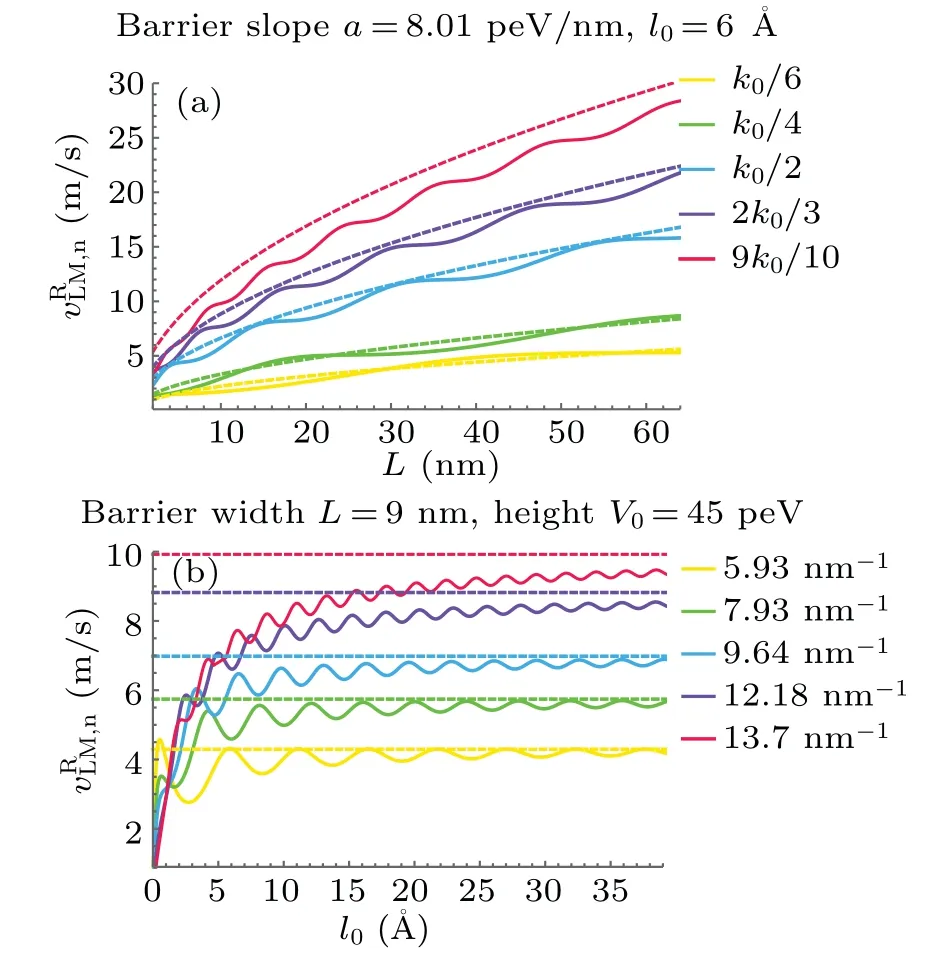
Fig.10.The dependences of reflective Larmor velocity vRLM,n for NETBs on barrier width L and the barrier distance l0,respectively.The dashed curves or lines are the corresponding velocities of free particles.(a)The vRLM,n with varying barrier width L of an NETB with a fixed barrier slope-8.01 peV/nm and the barrier distance l0=6 °A.(b)The vRLM,n with varying the barrier distance l0 for an NETB with width L=9 nm and height V0=45 peV.
Although we have shown that there is no sign of a barrier width saturation effect through the velocities defined with the phase and Larmor times, the absence of a barrier saturation effect does not necessarily validate that the Larmor or phase times have the traversal time meaning,since we find that whenk ≤k0,a largerkmeans a smaller velocity,in contradiction to the classical intuition that a largerkmeans a larger velocity,at least in free space.
5.Summary
In this paper, we study the Wigner phase time, Larmor time and dwell time for a particle tunneling through TBs,especially the positive-slope and negative-slope ETBs,abbreviated as PETBs and NETBs,respectively.The transmitted phase or Larmor times do not distinguish whether the steeper edge is on the left or right side,provided that the pair of TBs are MS.This is simply due to the fact that the transmission amplitudes for a pair of MS one-dimensional barriers are exactly the same,regardless of the barrier shape.
By plotting the dwell,reflective phase and Larmor times as functions of wave numberk-spectrum and barrier parameter, such as the slope of a barrier, we demonstrate that these times have quite distinct behaviors for a pair of MS PETBs and NETBs.This may indicate that these times are barriershape sensitive.In comparison,dwell time is much smoother than the other two times since it averages over all scattering channels,while the oscillatory behavior of the other two times may be signals of the interference between the transmitted and reflected partial waves scattered by the two edges of a barrier.In short,the tunneling time for an NETB is much smaller than that for an MS PETB given the same wave numberk.This may be explained by the fact that a particle with energy lower than barrier heightV0is more likely and quickly to be reflected by the vertical edge of an NETB than by the soft edge of an MS PETB.



The deficiency of our stationary state treatment is that the results may not be fully convincing; however, we can view them as the monochromatic limit of the wave packet method.In short, the main results are summarized as follows.(i)The tunneling times for TBs are barrier-shape sensitive and there seems to be no barrier width saturation effect.(ii) When the energy of the particle is well inside the tunneling region, the transmitted times lose traversal meaning, as supported by the anti-intuitive behaviors from the velocity analysis for ETBs.(iii)When the particle is capable of surpassing the barrier classically, the times may still be meaningful.The temporal behavior of the tunneling process needs to make full use of some novel quantum switch[62,63]or attosecond processes and thus an investigation of tunneling times based on the strict wave packet method is necessary and urgent, and will be explored in the future.
Appendix A:Dwell times for a general interval
The dwell times in the interval[-zl,(zr+L)]for a PETB and[-(zl+L),zr]for the MS NETB are

Appendix B:Eigen-wave function
The eigensolutionφk(z) for a particle tunneling through an NETB,Vtri(-z)=-Θ(-z)Θ(L+z)az, MS to the PETBVtri(z),is
From the continuity equations atz=-L,0,we can obtain the solution as below:
where again we setα=1 and define the reflection and transmission amplitudes asRn≡β/α,Tn≡γ/α,respectively.
The eigensolutionφk(z)for a particle tunneling through a TB with a general shapeVtri(z)=Θ(l1+z)Θ(-z)a(z+l1)+Θ(z)Θ(l2-z)b(l2-z)is

where as the definitions for the eigensolution of ETBs, we have also defined

Appendix C: The various components in the eigenfunctions in the presence of magnetic fields
The various amplitudes in the eigenfunction for the Larmor time in Eq.(21)are
wherea=1,2.In other words,it looks like that the upper and lower reflective and transmitted amplitudes interchanged whenθ=0↔θ=π.As for an NETB,since the situation is similar,we do not write the corresponding amplitudes explicitly.
Substituting Eqs.(C1)and(C2)into Eq.(22),we can obtain the explicit formulas for the transmitted and reflective Larmor times,respectively.Substituting Eq.(C5)with the choice ofθ=πwill lead to equivalent Larmor times and thus will not be shown here.The transmitted Larmor time is



Appendix D: Some preliminary results for a generic type of TB
With the scattering coefficients such as Eqs.(B7) and(B8), we can obtain tunneling times for a TB with a generic shape by the time definitions shown in the main context.The TB does not include the type of triangle with an obtuse angle on the bottom edge.A sketch of TBs with general shapes and the relative probability densities for a left incoming particle scattered off the barriers is shown in Fig.D1, where the two TBs are MS with barrier heightAand widthL=l1+l2.The widths are separated by the vertical lines(represented by the solid thin lines) passing the apexes tol1:l2=1/2, 2/1 for Figs.D1(a)and D1(b),respectively.Since the calculation of the tunneling times for a TB of generic shape is tedious,we only present the results of the Larmor and phase times directly.
To obtain the Larmor time measured by spin precession,we have to figure out the coefficients in the ansatz similar to Eq.(21)below:


Fig.D1.Sketch map of the probability density distribution |ψk(z)|2 for a particle tunneling through a pair of MS TBs with the barrier height A and width separation ratio l1 :l2 =1/2 for (a) and l1 :l2 =2:1 for (b), where the k are shown in the legends.

To see whether the phase and Larmor times of TBs are affected by the barrier width saturation effect, we also define the velocities in a fashion similar to those of ETBs defined in Section 4.The results are directly shown in Fig.D3, where we see there are no such effects for general TBs just as for ETBs, since the velocities approach or oscillate around constants whenLis large enough.The lack of dashed red curves in Fig.D3 is because the values are much larger than the plot ranges and these curves also oscillate around constants.Moreover,from Fig.D4,we can see that the presence of barriers indeed retarded the propagation of the tunneling particle where the curves are all below the dashed yellow lines representing free particles whenk <k0.However,whenk >k0,the curves representing barrier width separation ratios 1:4 and 1:14 all turn to much higher values than the velocities of free particles,while the reflective Larmor or phase velocities for the barriers with much gentler left slopes correspond tol1:l2=4:1 and 14:1 still remains smaller thanvfuntilkis significantly larger thank0, where oscillation behaviors become transparent both for phase and Larmor velocities.In contrast,the velocities defined with the transmission phase and Larmor times are much larger than the velocities of the free particles whenkis significant smaller thank0;whenkis close or even larger thank0,the barrier seems retard the propagation of transmitted particles,in contradiction to classical intuitions.Due to space limitations, we leave detailed investigations of the tunneling times for generic shapes of TBs for future works.
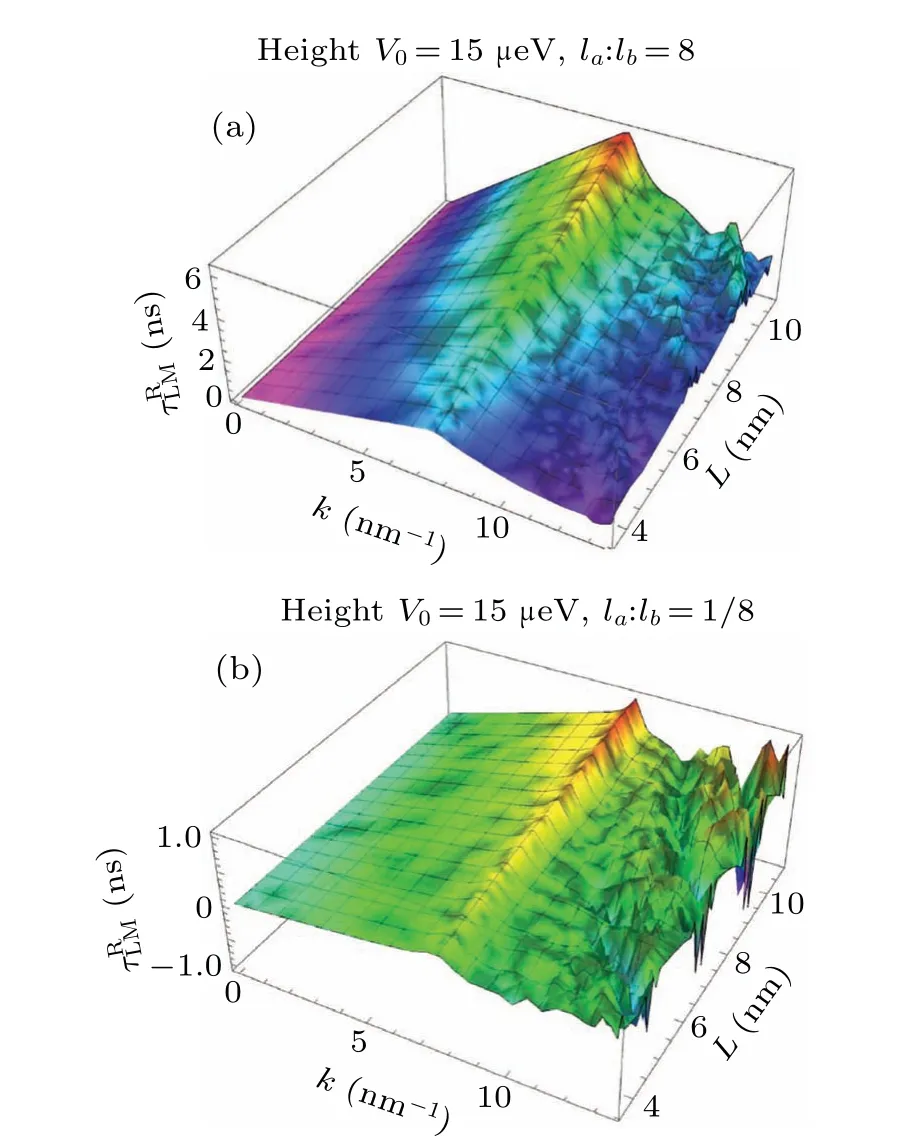
Fig.D2.The reflected Larmor times as functions of the barrier width L and the wave number k of the incoming particle for a pair of MS TBs with width separation ratios(a)8:1 and(b)1:8,respectively.

Fig.D3.The reflective velocities defined from the Larmor and phase times for asymmetric TBs with V0 = 15 µeV.The solid and dashed curves in the two subfigures correspond to barrier width separation ratios l1 :l2 =4:1 and l1 :l2 =1:5, respectively.The velocities for particles with different wave numbers are shown with different colors in the legends.(a)The reflection Larmor velocities,where the magnetic field is set to be 1 mG.(b)The reflection phase velocities.
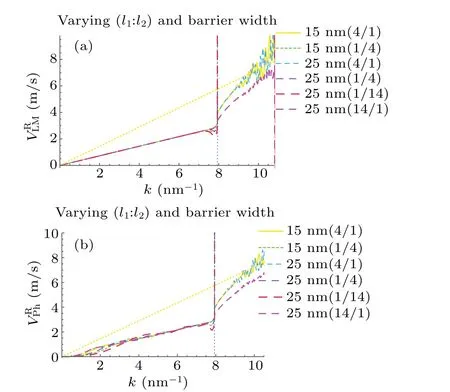
Fig.D4. The comparison of reflective Larmor and phase velocities with the corresponding free particles.The dashed yellow lines correspond to the velocity of free particles and the dotted vertical lines correspond to the critical wave number k0 =/¯h=7.93 nm-1.The different colors correspond to barrier width 25 nm and 15 nm with different width separation ratios.(a)The reflection Larmor velocities,where the magnetic field is set to be 1 mG.(b)The reflection phase velocities.
Acknowledgements
Project supported by the National Natural Science Foundation of China (Grant Nos.11974108, 11875127, and 12211530044) and the Fundamental Research Funds for the Central Universities(Grant No.2020MS052).
- Chinese Physics B的其它文章
- A multilayer network diffusion-based model for reviewer recommendation
- Speed limit effect during lane change in a two-lane lattice model under V2X environment
- Dynamics of information diffusion and disease transmission in time-varying multiplex networks with asymmetric activity levels
- Modeling the performance of perovskite solar cells with inserting porous insulating alumina nanoplates
- Logical stochastic resonance in a cross-bifurcation non-smooth system
- Experimental investigation of omnidirectional multiphysics bilayer invisibility cloak with anisotropic geometry

