基于NLMS和Autoformer的滚动轴承RUL预测

刘康宁,徐遵义,李 晨,闫春相

(山东建筑大学 计算机科学与技术学院,山东 济南 250101)

0 引 言

滚动轴承是建筑机械设备中应用非常广泛的关键零部件。由于建筑机械设备运行条件恶劣,滚动轴承较易发生故障。轴承故障轻则造成经济损失,重则危及生产安全[1]。准确预测滚动轴承剩余使用寿命(Remaining Useful Life,RUL)对维护设备稳定运行、保障生产安全具有重要的现实需求和应用价值。

随着传感器技术与信号处理技术的发展,根据大量历史传感器数据对滚动轴承退化信息进行建模的数据驱动方法,尤其是深度学习方法,已成为滚动轴承RUL预测主流发展方向[2]。根据深度学习模型结构可分为基于循环神经网络(Recurrent Neural Networks,RNNs)模型的RUL预测方法和基于Transformers长序列预测模型的RUL预测方法。RNNs模型虽已在滚动轴承RUL预测领域取得较好效果[3-4],但囿于模型结构,此类模型难以建模长距离依赖关系,无法充分利用长输入序列中隐含的退化特征;同时,RNNs模型的串行计算方式严重制约了模型运行速度[5]。Transformer模型采用自注意力机制(Self-attention Mechanism)捕捉输入序列中任意向量之间的依赖关系,在解决RNNs模型的长距离依赖问题的同时实现了并行计算[6]。周哲韬等提出基于Transformer模型的滚动轴承RUL预测方法,较好地提升了预测准确率[7]。Zhou等对Transformer模型的自注意力机制与解码方式进行改进,提出了Informer模型[8]。李广福等使用Informer模型挖掘出退化指标与滚动轴承退化趋势的复杂映射关系,通过实验证明了该方法相对GRU(Gated Recurrent Unit),LSTM(Long Short-Term Memory)等RNNs模型方法的先进性[9]。然而,Transformer,Informer等模型中的自注意力机制难以从复杂长时间序列中分解出可靠的时序依赖,且此类逐点聚合特征的方式会造成信息利用瓶颈。

Autoformer模型是对Transformer,Informer等模型的有效改进：提出一种序列分解模块(Series Decomposition Block),可从复杂时间模式中渐进地分解出趋势项(trend-cyclical)与周期项(seasonal);提出一种自相关机制(Auto-Correlation Mechanism)代替自注意力机制,使用序列级连接聚合周期依赖项(Period-based dependencies),打破信息利用瓶颈的同时实现了O(LlogL)复杂度[10]。

鉴于振动信号具有对轴承状态变化响应迅速、容易提取等优点,该文采用振动信号进行滚动轴承RUL预测。在实际生产环境中,采集到的振动信号往往具有非线性、非平稳和低信噪比等问题,因此需对其进行降噪处理。自适应滤波器使用自适应算法根据输入信号的时变统计特性自动调整数字滤波器权重,其参数设置受人为因素影响小,鲁棒性佳[11];相对于LMS(Least Mean Square)自适应算法,NLMS(Normalized Least Mean Square)自适应算法收敛速度更快、同时可避免长输入信号下的噪声梯度放大问题,更为适合对滚动轴承振动信号进行降噪。

该文将Autoformer模型引入滚动轴承RUL预测领域,提出一种基于NLMS自适应滤波器和Autoformer长序列预测模型的滚动轴承RUL预测方法。使用NLMS自适应滤波器对采集到的滚动轴承原始振动信号进行降噪,从降噪振动信号中分段提取时域特征,采用Spearman相关系数筛选出对滚动轴承RUL预测贡献较大且独立性较强的特征列,经归一化后形成多维特征集;利用Autoformer模型中序列分解模块与自相关机制建立多维特征集与滚动轴承RUL之间的分段非线性映射,实现滚动轴承RUL预测。

1 相关理论

1.1 NLMS自适应滤波器

NLMS自适应滤波器主要由参数可调数字滤波器与NLMS自适应算法组成[11],其结构如图1所示。

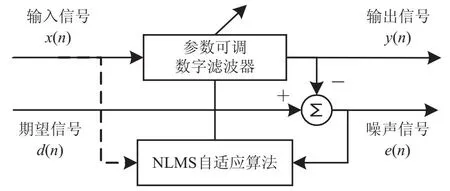
图1 NLMS自适应滤波器结构

NLMS自适应滤波器工作流程为：

(1)初始化滤波器权重w(0)、阶数L、步长因子μ与修正因子σ,确定输入信号x(n)、期望信号d(n);

(2)将x(n)输入滤波器,得到输出信号y(n);

(3)将d(n)与y(n)作差,得到噪声信号e(n);

(4)NLMS自适应算法使用x(n)的欧氏范数的平方对w(n)更新量进行归一化,以梯度下降的方式更新w(n),计算方法如式1所示。

(1)

其中,μ用于控制算法收敛速度;

(5)重复步骤2～步骤4至最大迭代次数或算法收敛,得到最优滤波器权重。

1.2 Autoformer模型

Autoformer模型主要由编码器、解码器组成[12],模型架构如图2所示。

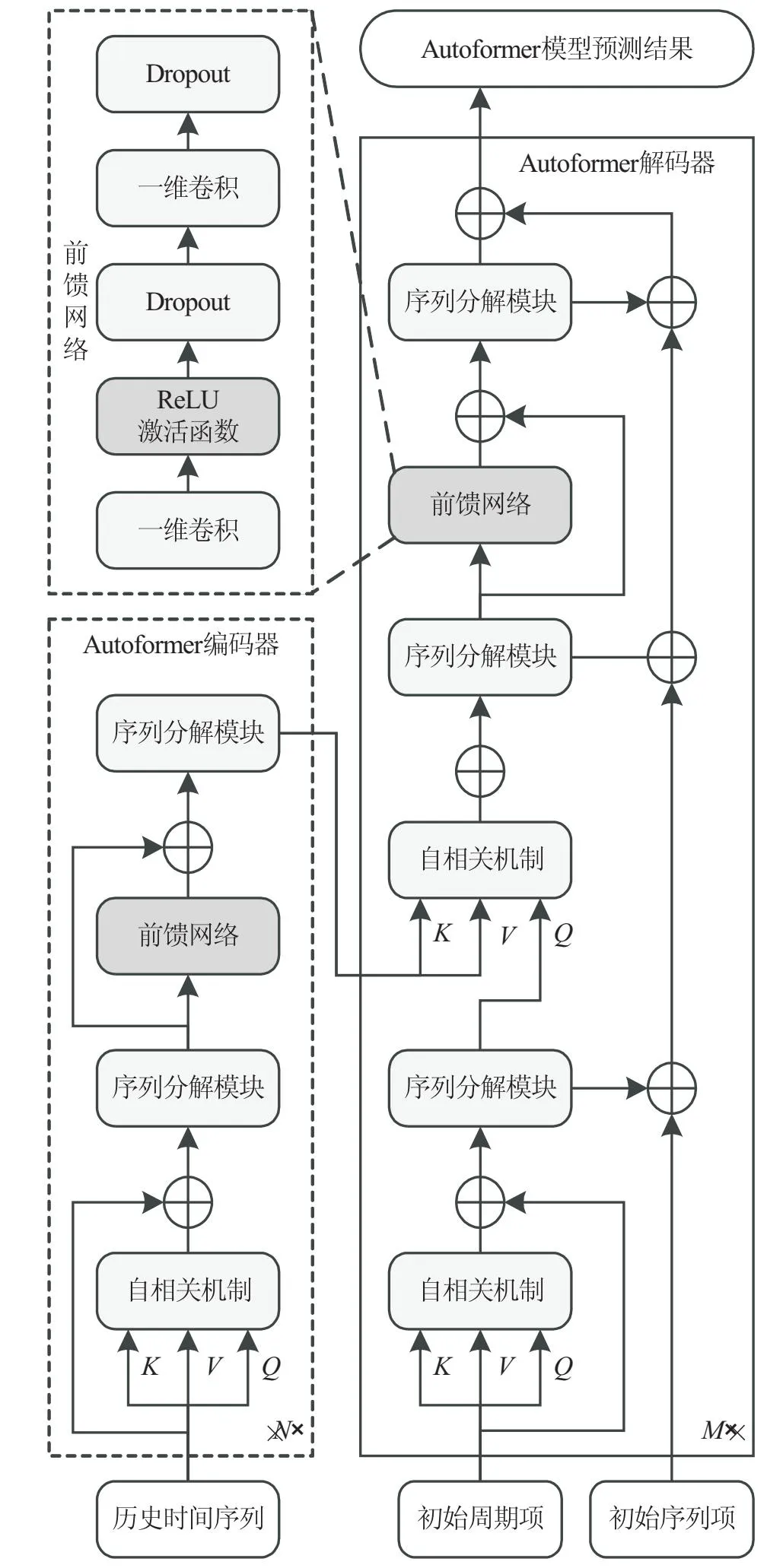
图2 Autoformer模型架构

每层编码器与解码器中堆叠序列分解模块、自相关机制、前馈网络(主体为一维卷积)。编码器的输入为历史时间序列,通过序列分解模块逐步分离并输出历史周期性信息;解码器的输入为周期项与趋势项信息,对趋势项与周期项分别建模：对于周期项,使用多头自相关机制聚合周期依赖项;对于趋势项,使用逐步累积方式从隐变量中提取趋势信息;最终输出模型预测结果。

1.2.1 序列分解模块

Autoformer模型中的序列分解模块用于从复杂时间模式中渐进地分离出趋势项与周期项。趋势项与周期项计算方法如式2和式3所示。

χt=AvgPool(Padding(χ))

(2)

χs=χ-χt

(3)

其中,χ为时间序列中的待分解隐变量,χt与χs分别为趋势项与周期项;Padding()操作用于维持序列长度,AvgPool()操作用于平滑周期项,从而突出趋势项。

1.2.2 自相关机制

自相关机制基于序列周期性设计。多头(multi-head)版本的自相关机制结构如图3所示。

图3 多头自相关机制

基于随机过程理论,通过计算原序列{χt}与τ滞后序列{χt-τ}的自相关系数Rχχ(τ)发现周期依赖项。基于Wiener-Khinchin理论,自相关系数Rχχ(τ)可通过快速傅里叶变换(Fast Fourier Transform,FFT)得到,Rχχ(τ)计算方法如式4～式5所示。

(4)

(5)

其中,τ为滞后项,Sχχ(f)为信号的频域表示,F与F-1分别表示FFT及其转置运算,F*表示F的共轭运算。

使用TopK()操作取前k个使得自相关系数最高的周期长度,避免挑选到无关甚至相反相位;然后根据估计的周期长度使用Roll()操作进行信息对齐,之后聚合不同周期下相似子序列的时延信息。时延信息聚合过程如式6～式8所示。

τ1,…,τk=argTopk(RQ,K(τ)),τ∈{1,2,…,L}

(6)

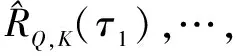
(7)

AutoCorrelation(Q,K,V)=

(8)

2 基于NLMS和Autoformer的滚动轴承RUL预测

基于NLMS自适应滤波器和Autoformer模型的滚动轴承RUL预测流程如图4所示。

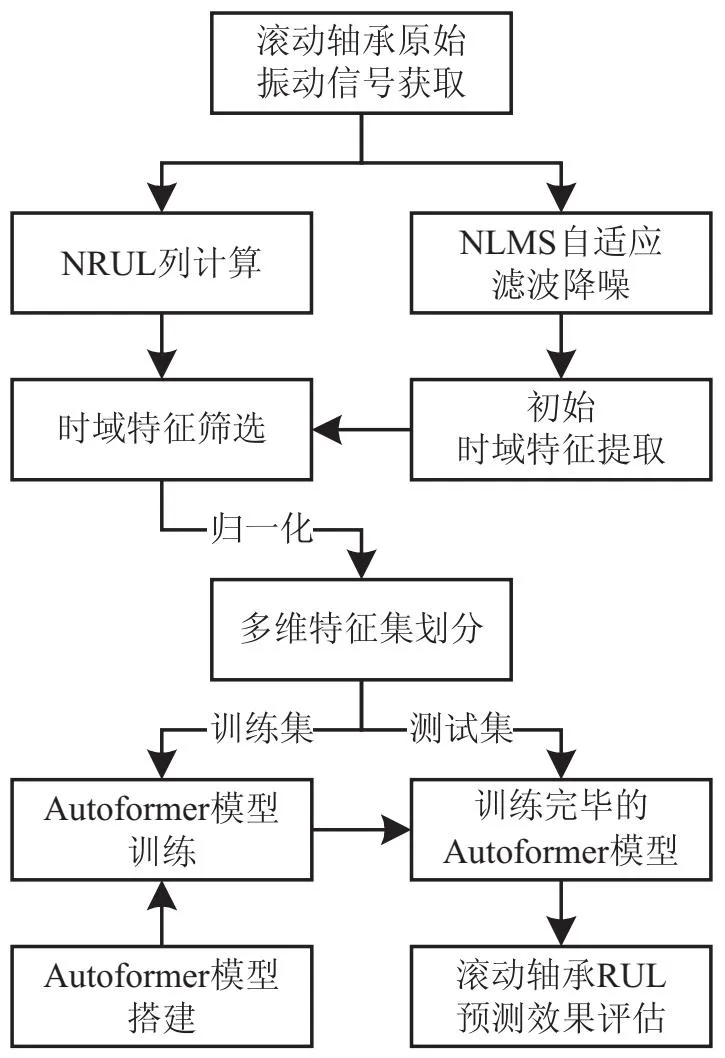
图4 基于NLMS和Autoformer的滚动轴承RUL预测流程

具体流程为：

(1)数据准备。

(a)获取滚动轴承原始振动信号;

(b)根据滚动轴承原始振动信号各样本段采样时间构建归一化剩余使用寿命(Normalized Remaining Useful Life,NRUL)列作为数据集标签;

(2)数据预处理。

(a)数据降噪：使用NLMS自适应滤波器对滚动轴承原始振动信号进行降噪;

(b)特征提取：从降噪振动信号中分段提取常用时域特征;

(c)特征筛选：对各时域特征列结合NRUL列进行Spearman相关性分析,筛选出对滚动轴承RUL预测贡献较大且独立性较强的特征列;

(d)数据集划分：对选取的各时域特征列经归一化后形成多维特征集;将多维特征集按比例划分为训练集与测试集;

(3)模型搭建与训练：初始化Autoformer模型超参数;将训练集作为Autoformer模型的输入,NRUL预测值作为模型的输出,对Autoformer模型进行训练;

(4)模型评估：将测试集输入训练完毕的Autoformer模型,使用均方根误差(Root Mean Squared Error,RMSE)、平均绝对误差(Mean Absolute Error,MAE)两个评价指标对模型预测效果进行评估。

3 实验验证与分析

该文采用FEMTO-ST研究所(法国贝桑松)提供的PHM 2012数据集进行仿真实验。PHM 2012数据集由PRONOSTIA实验平台通过多次加速轴承退化实验采集,实验平台结构如图5所示[13]。

图5 PRONOSTIA实验平台

PHM2012数据集包含三种工况(径向载荷力和转速)下轴承振动数据与温度数据,其中径向载荷力用于加速轴承退化过程,各工况参数设置如表1所示。

表1 PRONOSTIA实验平台三种工况参数设置

振动信号由水平方向与垂直方向的两个加速度传感器进行采集,采样频率为25.6 kHz,采样间隔为10 s,一个采样周期长度为0.1 s。当振动信号水平振幅超20 g时认为轴承失效,获得轴承全寿命周期振动信号。该文取分属三种工况的轴承1_1、轴承2_1及轴承3_1的全寿命周期振动信号作为研究对象。轴承1_1全寿命水平振幅如图6所示。

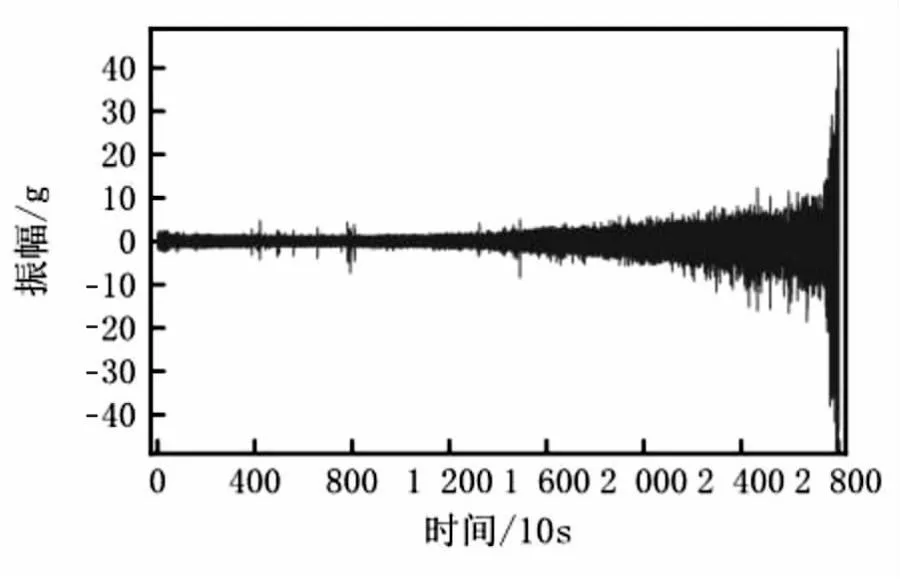
图6 轴承1_1全寿命水平振动信号波形

由图6可知,可按振动信号振幅变化将轴承1_1全寿命周期大致分为3个阶段[14]。第1样本段至第1 150样本段为健康阶段：此阶段信号振幅基本保持平稳;第1 151样本段至第2 710样本段为退化阶段：由于退化事件(如磨损、点蚀等)的发生,此阶段信号振幅较前一阶段逐渐增大;第2 711样本段至第2 803样本段为失效状态：由于退化事件进一步发展,此阶段信号出现跳变,信号振幅急剧增大,轴承失效。

不同类型、不同工况下的滚动轴承RUL衰减规律不尽相同。为保持模型的泛用性,该文构建NRUL真实值列作为数据集标签。各样本段对应NRUL真实值计算公式如式9所示。

(9)

其中,STt表示第t样本段采样时间。可见对于轴承全寿命周期数据,轴承初始状态即ST1时对应NRUL真实值为“1”,轴承退化至失效(Run-to-Failure,RTF)状态即STn时对应NRUL真实值为“0”;可较好地描述NRUL真实值随时间衰减规律。

3.1 数据预处理

数据预处理的主要过程包括数据降噪、时域特征提取及筛选、数据归一化等。

3.1.1 数据降噪

为抑制背景噪声、凸显退化信息,使用NLMS自适应滤波器对滚动轴承原始振动信号进行降噪。

期望信号的选择对自适应滤波器性能有较大影响,为引导滚动轴承原始振动信号向期望信号靠拢的同时保留更多关键信息,在以滚动轴承原始振动信号为输入信号的前提下,该文选用经滑动平均处理的输入信号作为期望信号。采用的NLMS自适应滤波器阶数设置为32,步长因子设置为1e-4,修正因子设置为1e-3。轴承1_1第1样本段水平振幅经上述参数设置的NLMS自适应滤波降噪前后对比如图7所示。

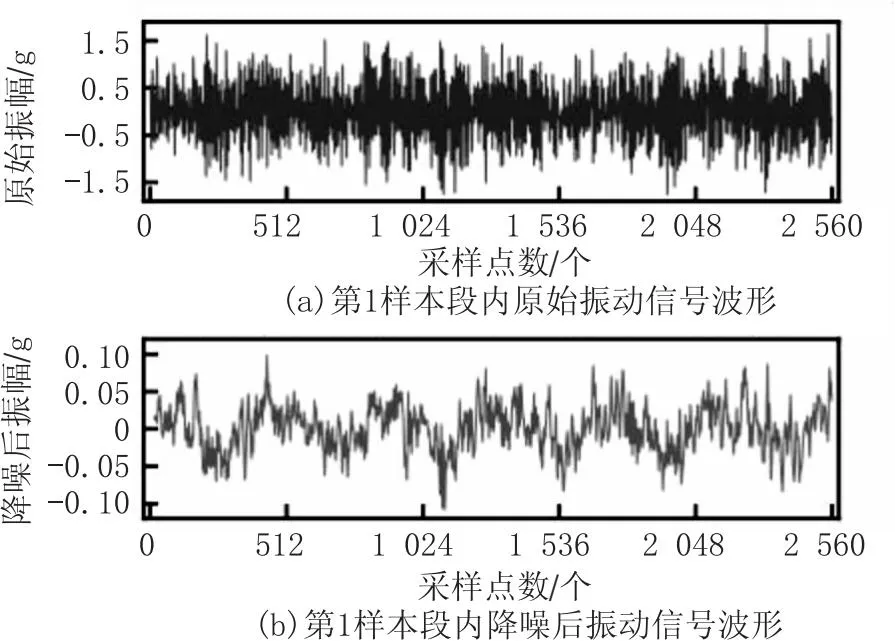
图7 轴承1_1第1样本段振动信号降噪前后波形对比

由图7(a)、图7(b)可知,经NLMS自适应滤波降噪后,高频率与高幅值的噪声组分被有效抑制,数据振荡现象得到极大缓解,轴承振动信号变得更为集中与平滑;同时,原始振动信号的时变趋势、跳变等有用信息得到较好保留。故NLMS自适应滤波器可较好地对滚动轴承原始振动信号进行降噪。

3.1.2 特征提取及筛选

分段聚合近似(Piecewise Aggregate Approximation,PAA)将序列均分成段,每个分段使用一个或多个特征值来表征,最终得到新的特征序列,可同时起到压缩数据量与进一步降噪的作用[15]。该文基于PAA的思想对滚动轴承振动信号进行特征提取。

滚动轴承振动信号时域统计特征可解释性强、易于提取且计算量小,多维时域特征可直观、全面地反映轴承退化状态[16]。为维持数据量与预测效果的平衡,对分段长度为8的振动信号序列分别提取多维振动信号时域特征。参考文献[17-18],该文选择的初始时域特征如表2所示。

表2 初始时域特征

冗余特征不仅会增加计算量、降低模型运行速度,还可能影响轴承RUL预测的准确率。该文通过计算各特征列与NRUL真实值列之间的Spearman相关系数进行特征筛选。

特征筛选过程中,保留与NRUL真实值列相关系数绝对值较大的特征列。同时,若特征列两两之间相关性较高,则仅保留两者中与NRUL真实值列相关性更高的一列,删除另外一列。最终选择的对滚动轴承RUL预测贡献较大且独立性较强时域特征为：方根值、峰值、峭度值、脉冲因数、峭度因数。

将保留的各列时域特征分别进行数据归一化,形成多维特征集。按照3∶1的比例将多维特征集划分为训练集与测试集。

3.2 模型训练与结果分析

该方法中Autoformer模型基于Pytorch 1.12.0框架实现,使用CUDA 11.6在NVIDIA GeForce RTX 3090 GPU中进行训练与测试。

将训练集输入Autoformer模型进行训练。采用的Autoformer模型由2层相同的编码器与1层解码器组成,模型维度为512;采用ADAM优化算法自适应调整学习率,初始学习率设为1e-4并随机初始化权重矩阵,设定值为0.05的Dropout防止模型过拟合,采用均方误差(Mean Squared Error,MSE)为损失函数,选定GELU(Gaussian Error Linear Unit)为激活函数。

将测试集输入训练完毕的Autoformer模型,根据输出的滚动轴承NRUL预测值计算RMSE和MAE,对模型预测效果进行评估。两种评价指标均可防止正负误差相互抵消,且数值越小代表预测效果越好。两种评价指标计算如式10、式11所示。

(10)

(11)

其中,n为测试集样本总数量,NRULT为滚动轴承NRUL真实值,NRULP为滚动轴承NRUL预测值。

文献[7]、文献[9]已分别证明Transformer模型、Informer模型相对GRU、LSTM、双向LSTM等主流RNNs模型在滚动轴承RUL预测领域的先进性。使用与Autoformer模型参数一致的Transformer模型、Informer模型与文中Autoformer模型建立对比实验,以验证Autoformer模型在滚动轴承RUL预测领域的有效性与先进性。上述三种模型预测效果如图8所示。

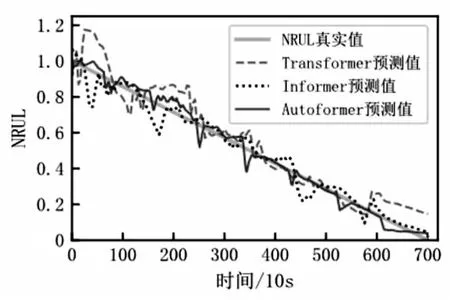
图8 各模型预测效果

为便于观察,图中预测曲线经窗口尺寸为8的滑动平均处理。由图8可知,三条预测曲线整体呈现与NRUL真实值曲线相似的下降趋势,表明Transformers模型在滚动轴承RUL预测领域具有巨大潜力;其中,Autoformer预测曲线最为贴近NRUL真实值曲线,且随着预测长度的增加,该曲线起伏逐渐减小;同时,观察到Autoformer预测曲线出现周期性尖锐跳变,而Transformer预测曲线与Informer预测曲线中此种现象不明显,推测这是由于Autoformer模型捕获到了轴承退化过程中的长周期性退化特征。证明了Autoformer模型相对其他Transformers模型在滚动轴承RUL预测领域的有效性与先进性。

此外,为验证NLMS自适应滤波器对降低预测误差具有重要作用,使用未降噪方法与文中方法进行对比。除在数据预处理阶段未对原始振动信号使用NLMS自适应滤波器进行降噪外,所述未降噪方法其余流程与文中方法相同。

Transformer模型方法、Informer模型方法、未降噪方法与文中方法在三种工况测试集上的评价指标值如表3所示。

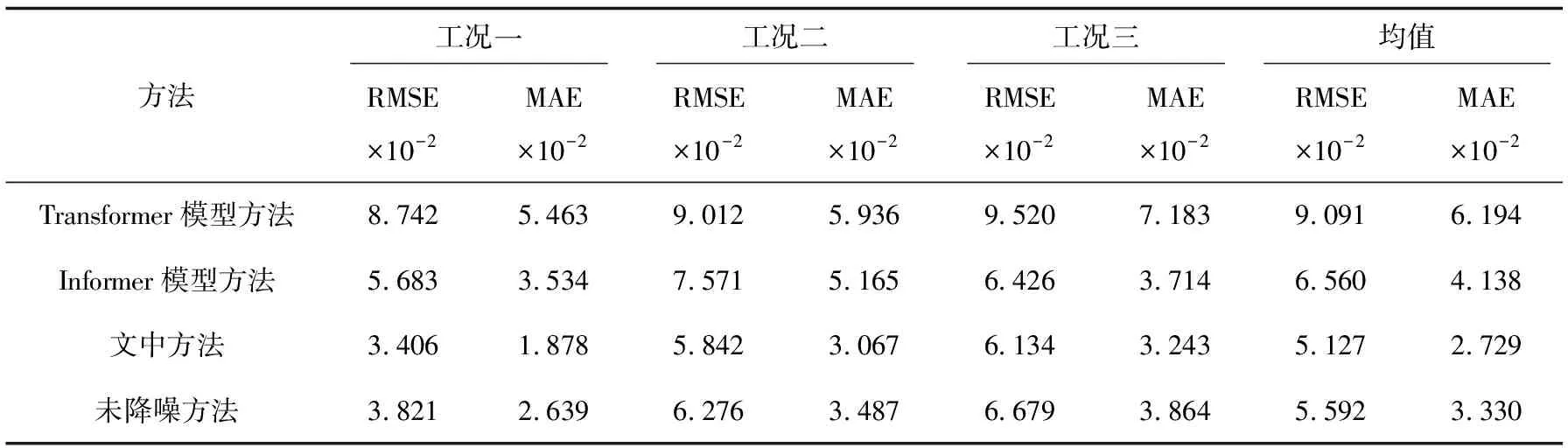
表3 PHM 2012数据集下各方法评价指标值

由表3可知：

(1)在经过相同的数据预处理后,与Transformer模型方法、Informer模型方法相比,文中方法预测误差在RMSE均值方面分别降低了43.60%和21.84%,在MAE均值方面分别降低了55.94%和34.05%;在三种工况中均可取得最低预测误差。进一步证明了基于Autoformer模型的滚动轴承RUL预测方法的有效性、先进性与泛化性。从模型设计思想分析：Transformer,Informer等模型的自注意力机制实现的是逐点特征聚合,此类离散方式未充分利用时间序列的连续性;而Autoformer模型的自相关机制实现的是高效的序列级连接,提升了信息利用率,更适用于滚动轴承RUL预测此类连续过程;从轴承退化机理分析：磨损是轴承退化的最主要形式,使得轴承振动信号振幅具有缓慢增大的趋势性;磨损、剥离等轴承内表面损伤通常会激起重复性的瞬态冲击,使得振动信号相应地表现出周期性瞬态脉冲;而Autoformer模型可很好地处理此类蕴含趋势性与周期性的长时序数据。

(2)在使用相同参数设置的Autoformer模型作为预测模型的情况下,与未降噪方法相比,文中方法预测误差在RMSE均值和MAE均值方面分别降低了8.32%和18.05%。可见NLMS自适应滤波器滤除了原始振动信号中混杂的大量噪声,避免了预测模型学习到无关甚至有害特征,从而降低了滚动轴承RUL预测误差。

为验证文中方法相对已有方法的先进性,将其与文献[9,19-20]所提方法在轴承1_1振动数据上的RUL预测评价指标值进行对比,如表4所示。

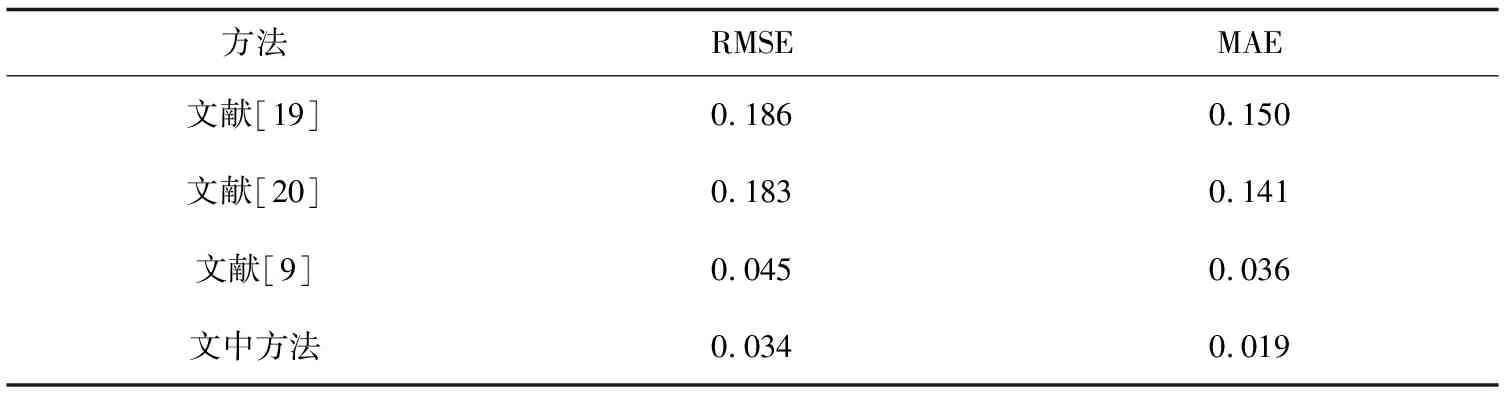
表4 文中方法与已有方法评价指标值

由表4可知,与已有方法中预测误差较低的文献[9]所提方法相比,文中方法预测准确率在RMSE与MAE两个评价指标上分别获得了24.4%与47.2%的提升,证明了文中方法的先进性。

为进一步验证文中方法的有效性与泛化性,使用西安交通大学与浙江长兴昇阳科技有限公司提供的XJTU-SY滚动轴承加速寿命试验数据集进行实验。该数据集共包含3种工况下15个滚动轴承的全寿命周期振动信号。振动信号由水平和竖直方向上两个加速度传感器采集,采样频率为25.6 kHz,采样间隔为1 min,一个采样周期长度为1.28 s[21]。取分属三种工况的轴承1_1、轴承2_1及轴承3_1的全寿命周期振动信号作为研究对象。经数据降噪、特征提取及筛选、数据集划分等步骤后,分别对与前述Autoformer模型参数一致的Transformer模型、Informer模型和Autoformer模型进行训练及测试。三种模型方法在三种工况测试集上的评价指标值如表5所示。

表5 XJTU-SY数据集下各方法评价指标值

由表5可知,文中方法相较Transformer模型方法、Informer模型方法在RMSE值分别降低了41.16%和2.81%,在MAE值分别降低了42.97%和4.56%,进一步证明了文中方法的有效性与泛化性。

4 结束语

提出一种基于NLMS自适应滤波器和Autoformer模型的滚动轴承RUL预测方法。经过实验分析,得到以下结论：

(1)NLMS自适应滤波器对降低预测误差具有重要作用。实验证明NLMS自适应滤波器可较好地对滚动轴承原始振动信号进行降噪;在使用相同参数设置的Autoformer模型作为预测模型的情况下,文中方法在评价指标上的表现优于未降噪方法;

(2)基于Autoformer模型的滚动轴承RUL预测方法具有有效性与先进性。实验证明Autoformer模型可有效建立多维特征集与滚动轴承RUL之间的复杂映射,文中方法的预测曲线与真实曲线最为贴合,与对比方法、已有方法相比预测误差最低,可更为准确地预测滚动轴承RUL。

尽管文中方法在滚动轴承RUL预测领域取得了较好效果,但仍未避免滞后预测现象的发生,后续可通过改进模型结构等措施减轻或消除滞后预测现象。