基于改进麻雀搜索算法的冷链物流路径优化

马青宇,邵松帅,刘博旭,孙 哲,龚光富,孙知信*

(1.南京邮电大学 江苏省邮政大数据技术与应用工程研究中心,江苏 南京 210023;2.南京邮电大学 国家邮政局邮政行业技术研发中心(物联网技术),江苏 南京 210023;3.安徽邮谷快递智能科技有限公司,安徽 芜湖 241300)

0 引 言

近年来,随着经济的高速发展,冷链物流的成本和时效性逐渐成为讨论的话题,目前已经有学者对冷链物流的车辆路径规划开展研究[1-3]。冷链物流不仅要考虑车辆的行驶路线,还需要充分考虑各个客户的服务时间窗口,以及车辆的容量、装载限制等因素,以达到最优化的配送效果。改进大规模车辆路径规划算法不仅能够提高物流配送的效率,降低物流成本,也能够提高客户的满意度和物流企业的竞争力。

带时间窗的城市间冷链物流路径规划属于VRPTW(Vehicle Routing Problem with Time Windows),是在VRP(Vehicle Routing Problem)的基础上引入每个城市期望送达的时间窗约束得到的,这体现了对冷链物流时效的高要求。VRPTW是NP-hard问题,求解方法可以分为精确求解算法和启发式算法。精确算法主要包括分支定界法[4]、列生成法[5]和动态规划算法[6]等。这类算法通过建立数学模型可以求得最优解,但是其求解所需的时间会随着问题规模的扩大而爆炸性增长[7]。这限制了精确算法在大规模问题上的应用。启发式算法主要包括蚁群算法[8]、遗传算法[9]、粒子群优化算法[10]和禁忌搜索算法[11]等。启发式搜索算法的优势是可以在合理的时间内求出较优的解,并且可以通过控制迭代次数平衡运算时间和运算精度。总的来说,求解大规模VRPTW时,选择启发式算法相较于精确求解算法有着较强的鲁棒性与可行性。

麻雀搜索算法是一种新型群智能优化算法,与其他具有代表性的算法相比有着较强的收敛速度与收敛精度,但是在求解一些复杂问题时,会陷入局部最优解,搜索停滞。针对麻雀搜索算法的不足,一些学者对其进行了改进。易华辉等[12]通过引入Tent混沌映射初始化种群、精英策略和自适应周期收敛因子在一定程度上防止算法陷入局部最优。严浩洲等[13]通过优化发现者与加入者的移动策略和引入柯西-高斯变异有效地提高了算法的收敛精度、稳定性和收敛速度。

目前,麻雀搜索算法在车辆路径规划问题,尤其是大规模VRPTW的应用较少,而且其算法本身也存在一些不足。基于此,该文对麻雀搜索算法进行了改进,并将改进算法应用于冷链物流路径优化问题的求解。

1 带时间窗的大规模城市间冷链物流的数学模型

1.1 问题描述

该文研究的问题可以具体表述为：有一个配送中心,多个城市,每个城市的位置、冷链商品需求,卸货所需时间已知,并且每个城市都有期望送达的时间窗,超出时间窗就要有一定的惩罚成本。每辆冷链物流运输车从配送中心出发,依次服务其所负责的城市,最后回到配送中心。在配送的过程中,冷链物流运输车服务城市的总需求量不得超过车辆最大载重量。在满足上述约束的条件下,合理规划每辆冷链物流运输车的配送路线,使得运输时间与惩罚成本的和最小[14]。

1.2 模型假设

为了简化模型,做出如下假设。

(1)假设每辆冷链物流运输车的型号载重量、速度一致,最大行驶里程不限。

(2)假设冷链物流运输车在城市间移动所需的时间为城市间的欧几里得距离。

(3)假设每个城市只能由一辆冷链物流运输车服务,且只能服务一次。

(4)假设每个城市的时间窗不存在冲突。

(5)假设冷链物流运输车不存在空闲等待,即总时间仅由车辆运行时间和卸货时间组成。

1.3 符号说明

模型符号说明如表1所示。

表1 模型符号说明

1.4 模型表示

模型的目标函数、约束条件由如下公式表示：

(1)

(2)

(3)

(4)

(5)

(6)

(7)

(8)

式1和式2表示两个参数的计算公式;式3表示最小化路径代价与时间窗偏移代价的和;式4约束了每个城市只能被服务一次;式5约束了每辆车携带货物不得超过最大载重;式6表示每个城市只能被一辆车服务;式7表示表示每辆车的起点和终点都是配送中心(0号城市);式8表示每辆车除配送中心的路径是一棵树(不存在环)。

2 麻雀搜索算法

2.1 标准麻雀搜索算法

麻雀搜索算法(SSA)是一种元启发式算法,由Xue等人于2020年提出[15]。该算法通过引入发现者-加入者模型,模拟了麻雀在自然界觅食与躲避天敌的行为。发现者是种群中能量值较高(适应度较高)的个体,在种群中引导加入者进行搜索。发现者和加入者中有一部分起到躲避天敌作用的警戒者。

发现者、加入者和警戒者的行为可以用以下公式表示[16]：

发现者：

(9)

加入者：

(10)

预警者：

(11)

式中,t代表当前的迭代次数,xi,j代表第i只麻雀第j维的值,iter_max代表最大迭代次数,Q是符合正态分布的随机数,r∈(0,1]代表预警值,ST∈[0.5,1]代表安全值。x_gworstj代表所有麻雀中适应度最差的个体第j维的值,x_gbestj代表所有麻雀中适应度最优的个体第j维的值,x_bestj代表发现者麻雀中适应度最优的个体第j维的值。X是正态分布随机数,且X～N(0,1)。fi代表第i只麻雀的适应度,fg_worst和fg_best分别代表所有麻雀中适应度最差和最优个体的适应度。

2.2 麻雀搜索算法的离散化

麻雀搜索算法针对的是连续问题,而VRPTW的解空间是离散的,所以需要将麻雀搜索算法离散化。在文中,连接离散空间与连续空间的桥梁是浮点数组的排序序列,离散化的具体过程如下：

假设一共有10个城市,3辆冷链物流运输车。图1是利用浮点数组进行离散化的过程。首先随机生成12个随机数,计算出数组中的排序,其中1～10代表城市编号,11和12是车辆分隔符。分隔符将不同车辆的配送路径分隔开,这个序列可以代表生成的路径。生成的路径如图2所示。

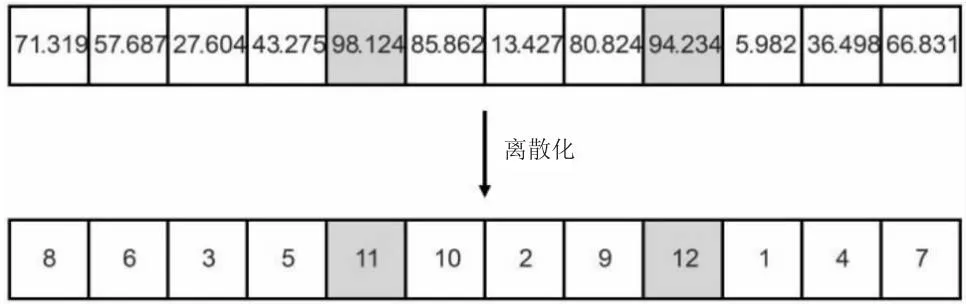
图1 浮点数组的离散化

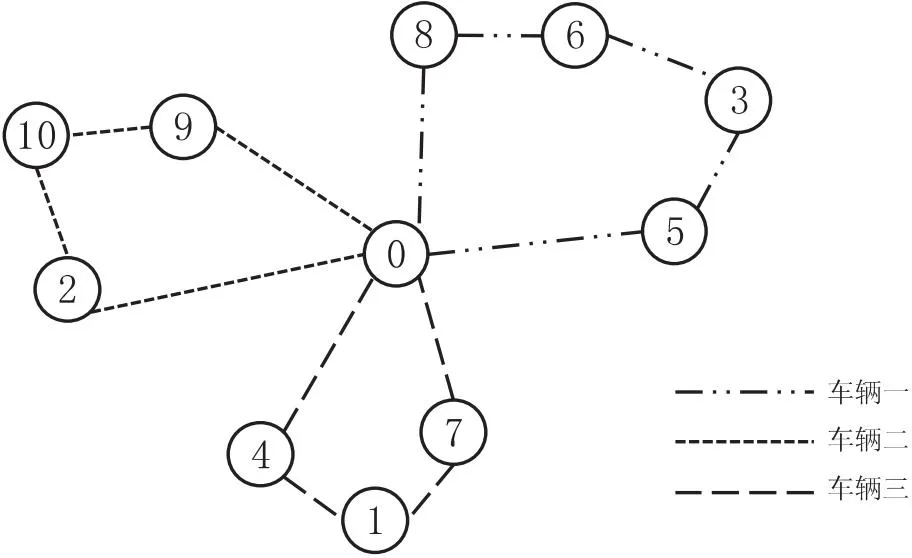
图2 离散化后生成的路径

2.3 改进的麻雀搜索算法

标准麻雀搜索算法在求解VRPTW时出现了收敛精度不够,易于陷入局部最优解的缺点。该文引入基于维度的邻域学习策略和包含动态因子的发现者位置更新公式,以提高算法的收敛精度和收敛速度。

2.3.1 基于维度的邻域学习策略

基于维度的邻域学习策略使得麻雀的信息来源不再拘泥于原有的麻雀层次体系,而是根据选择的邻域划分,接收多样化的信息,加强了麻雀之间的信息交流[17]。邻域的定义如图3所示。首先随机选择一只麻雀作为中心麻雀的邻域临界麻雀,其与中心麻雀的距离记为R,所有与中心麻雀距离小于等于R的麻雀称为邻域内麻雀,所有与中心麻雀距离大于R的麻雀称为邻域外麻雀。

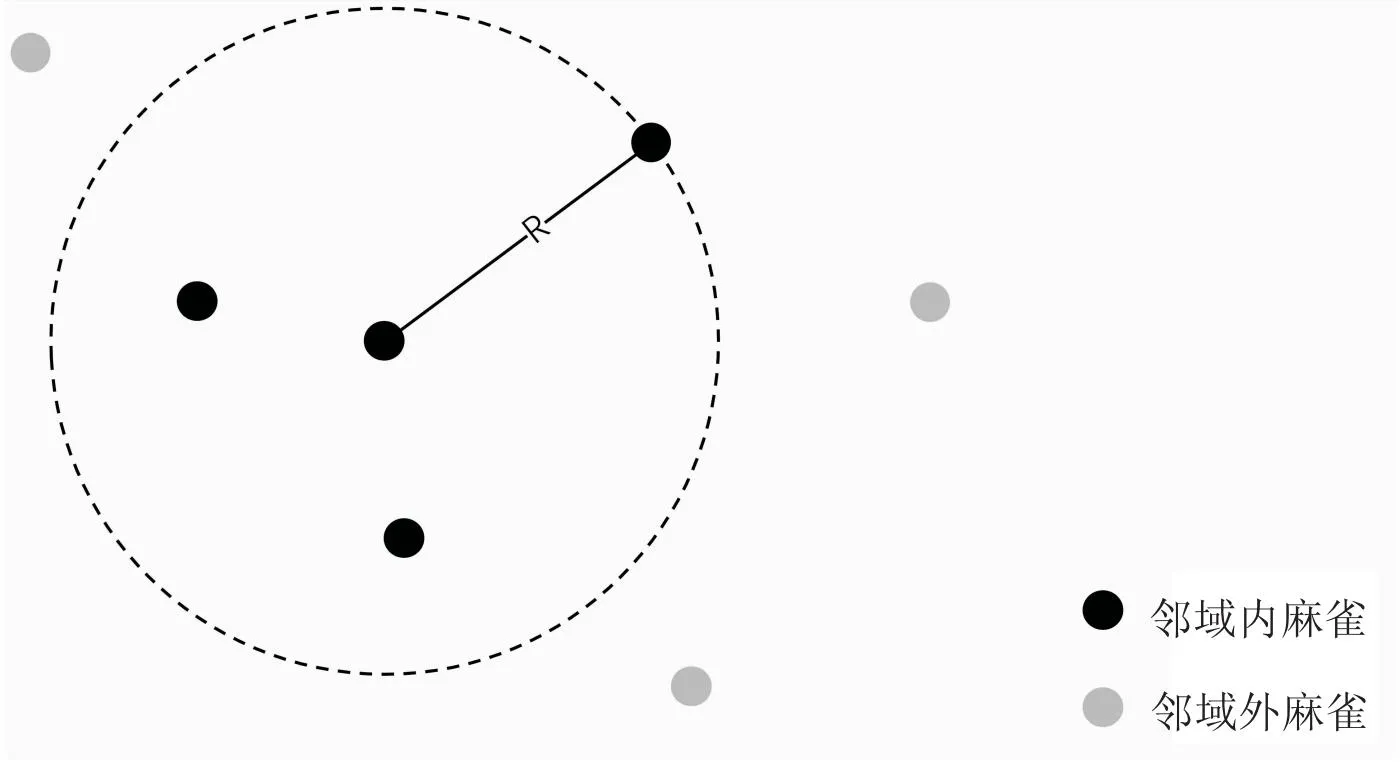
图3 麻雀的邻域模型示意图

通过计算每个麻雀的邻域,选择邻域内的麻雀进行信息交换,提高了子代麻雀信息来源的多样性,提高算法的收敛精度。

信息交流的公式如下：

Xi,j=

(12)

式中,Xw,j是被选中麻雀w在j维的值。

2.3.2 包含动态因子的发现者位置更新公式

发现者是整个种群的核心,是领导者。发现者的位置决定了种群的搜索方向。为了平衡种群的开发和勘探,该文在发现者的位置更新公式中引入了动态因子λ：

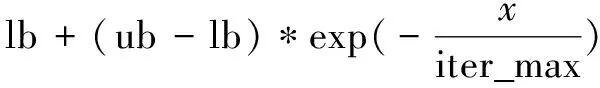
(13)

文中取lb=0.3,ub=0.7。动态因子的引入使得改进的麻雀搜索算法在前期注重于开发,后期注重于勘探,有利于加快收敛速度,提高收敛精度。改进后的发现者位置更新公式为：

(14)

2.3.3 改进算法的伪代码

改进麻雀搜索算法的伪代码如下所示：

Algorithm Improved-SSA

Input：

Max_iter：最大迭代次数;PD：发现者数量;SD：预警者数量;ST：预警值;N：麻雀种群数量

Output：

X_best,f_curve

1.初始化种群

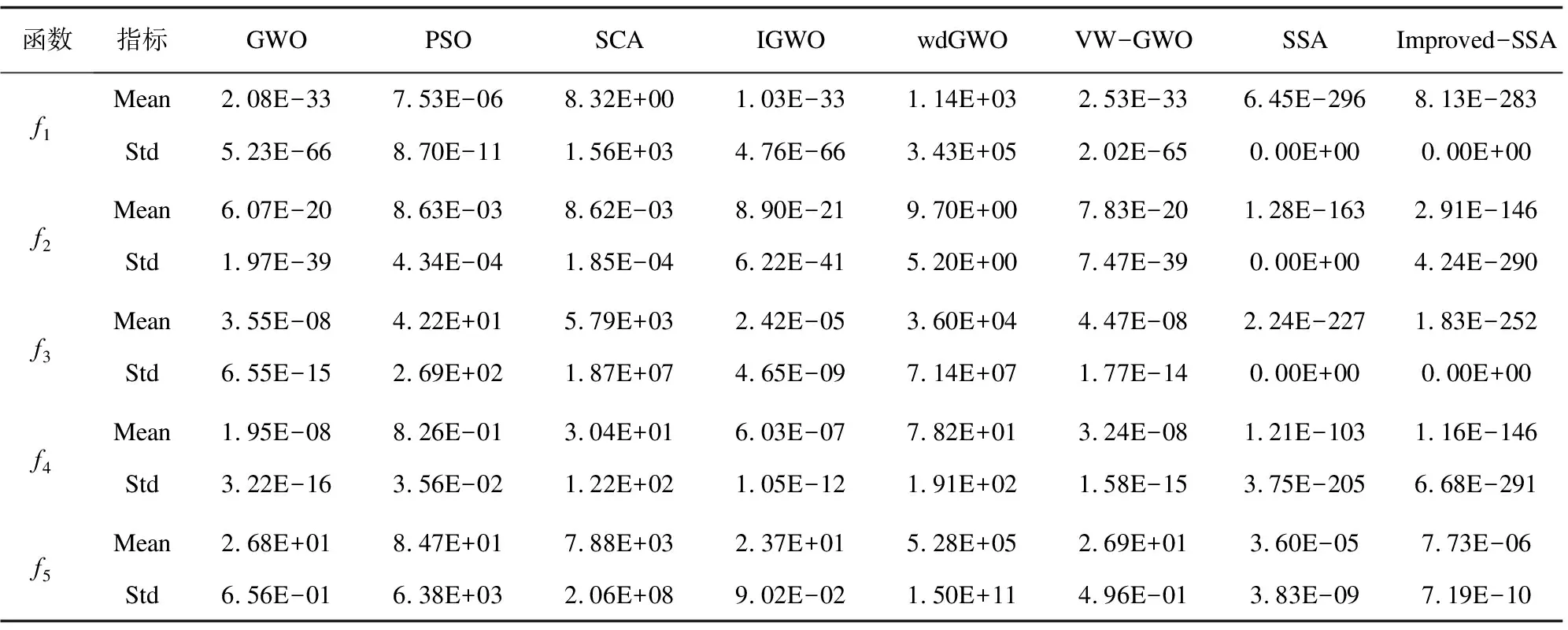
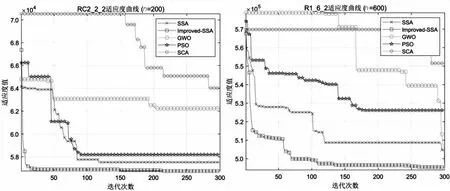
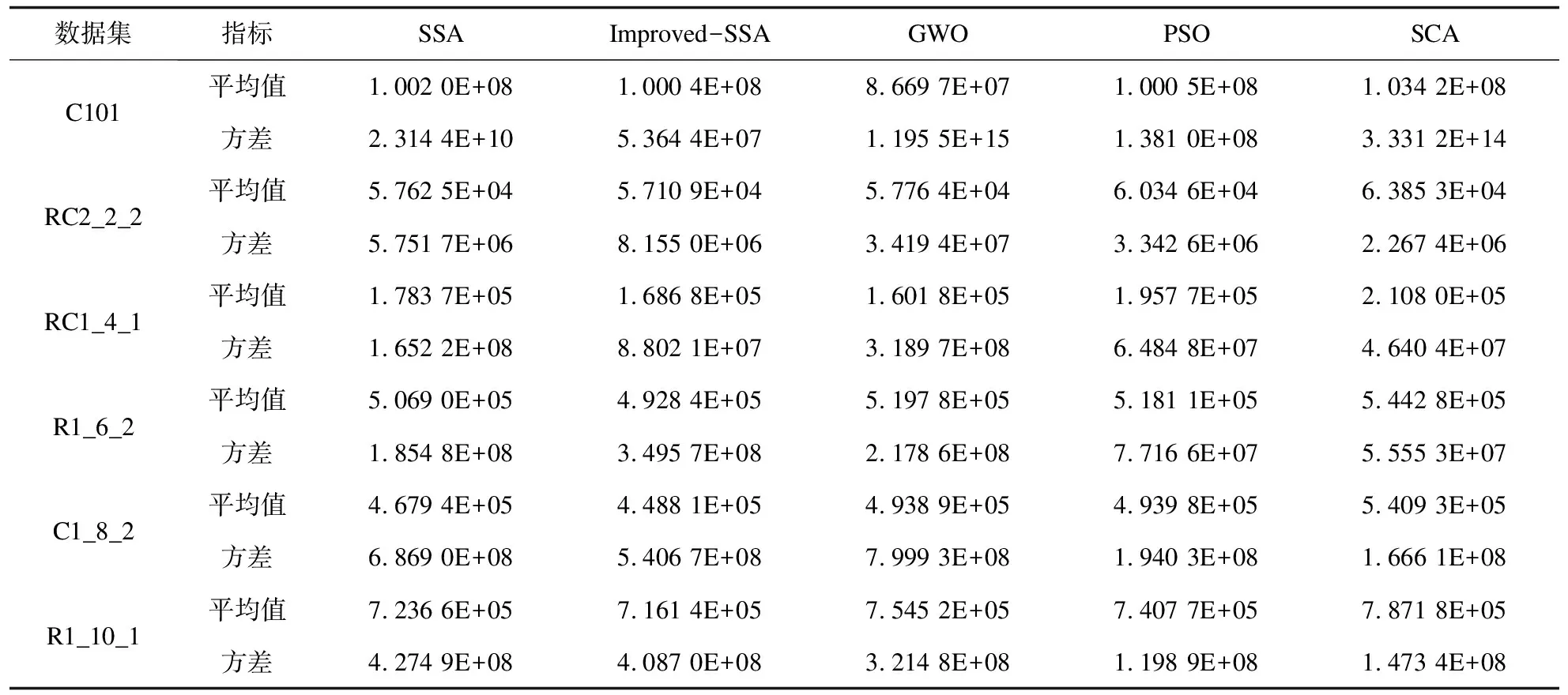
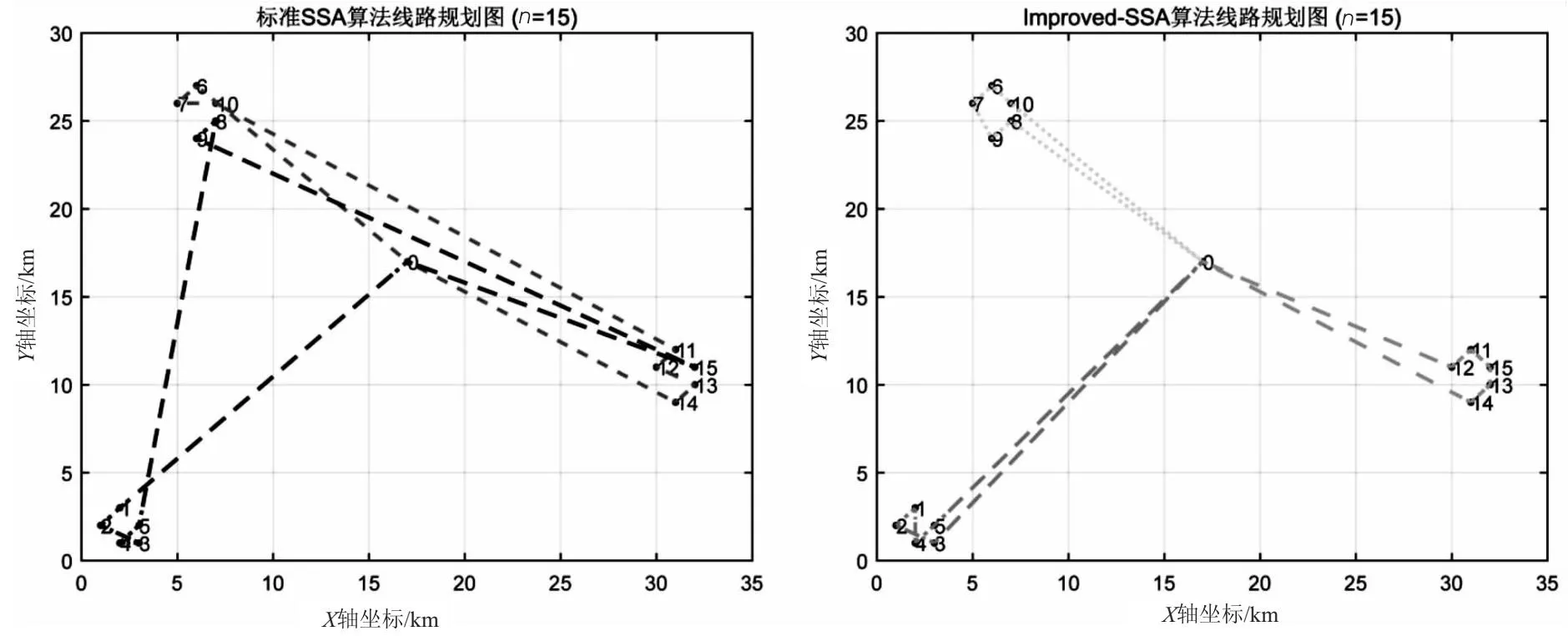
2.while (t

3. 对种群适应度排序,选出最优个体和最差个体

4. fori=1：PD

5. 使用式14更新发现者位置

6. fori=(PD+1)：N

7. 使用式10更新加入者位置

8. fori=1：SD

9. 使用式11更新预警者位置

10. fori=1：N

11. 选择邻域边界麻雀,计算邻域半径R

12. 筛选出邻域内的麻雀,随机选择一只,使用式12进行信息交流

13. 如果麻雀在新位置的适应度优于原位置,则更新麻雀位置,否则位置不变

14.t=t+1

15. end while

16. ReturnX_best,f_curve

3 实验分析

3.1 实验数据集

该文使用23个标准测试函数对改进的麻雀搜索算法进行测试,以衡量改进算法的搜索能力。同时,使用6个标准VRPTW数据集进行测试,以考察改进算法在冷链物流路径优化问题的求解效果。

3.1.1 标准测试函数

为了验证改进SSA算法的有效性,该文使用23个常用测试函数将改进SSA与标准SSA,GWO[18],PSO[19],SCA[20],IGWO22F[21],VW-GWO[22],wdGWO24F[21]进行比较。23个测试函数取自Mirjalili等所作实验[18],其中f1～f7是单峰基准函数,用于测试算法的开发能力。f8～f13是多峰基准函数,用于测试算法的勘探能力。f14～f23是符合基准函数,用于测试算法开发与勘探的平衡能力。为确保公平,该文对每种算法的参数统一设定：种群数量N=50,最大迭代次数Max_iter=500。

该文对23个测试函数分别进行30次独立重复实验,所得每个算法在每个测试函数上的平均值和方差如表2所示。实验结果表明,改进的SSA算法在15个测试函数上,求解的平均值排名第一,占比65%,求解结果也有较强的稳定性。特别是在f21～f23这种复杂函数上,改进的SSA算法有着绝对优势。总的来说,改进的SSA算法相较于标准SSA算法和其他元启发式算法有较强的竞争力,验证了改进的有效性。

表2 30次独立重复实验所得结果的平均值和方差

3.1.2 标准VRPTW数据集

该文选取了6组数据集进行实验对比,分别是C101[23],RC2_2_2[24],RC1_4_1[25],R1_6_2[25],R1_8_1[25],R1_10_1[25]。每个数据集包括城市坐标、货物需求量、送达时间窗、卸货时间。

3.2 实验结果分析

该文的评价指标是所有车辆的运行时间、卸货时间与超出时间窗的惩罚成本之和。

采用Matlab2022b对改进后的麻雀搜索算法进行对比,使用6个测试数据集对算法的性能进行评估,为了方便比较,图4是改进的SSA算法与标准SSA算法在其中2个测试数据集(RC2_2_2,R1_6_2)上的适应度迭代曲线。从图中可以看出,改进后的SSA算法在迭代前期有较大的收敛速度,在迭代后期的收敛精度也有较大的优势。

图4 改进SSA与标准SSA迭代曲线对比

(1)收敛分析。

如图4所示,标准SSA算法在前期的收敛速度不理想,并且后期容易陷入局部最优,导致搜索停滞。改进后的SSA算法不仅在前期的收敛速度十分出色,在后期也有一定的概率突破局部最优解。相较于其他典型算法,改进后的SSA算法也有收敛速度快、收敛精度高的特点。由实验结果可以看出,该文提出的改进策略可以有效提高算法的收敛速度和收敛精度。

(2)稳定性分析。

为了进一步评估改进的SSA算法,对两种算法在6个测试数据集上分别进行30次独立重复实验,每次独立重复实验取迭代次数为300。所得平均值与方差如表3所示。从表中数据可以看出,在75%的数据集上改进的SSA算法求解结果的平均值为最优,体现出较强的搜索性能。但是在求解结果的稳定性方面还有一定的改进空间。

表3 经过30次独立测试所得最优解适应度的平均值与方差

为便于可视化展示算法规划路径的效果,该文生成了小规模测试数据(n=15)并进行对比实验。测试过程中,超出时间窗惩罚系数为k=0.1。

测试所得的路径规划图如图5所示,其中不同样式的虚线代表不同冷链物流运输车的路径。其中标准SSA算法生成路径为：车辆1：0→6→7→10→11→12→13→14→0,车辆2：0→1→2→3→4→5→8→9→15→0,总花费(总时间与惩罚成本之和)为163.820 8;改进SSA算法生成的路径为：车辆1：0→1→2→3→4→5→0,车辆2：0→8→9→7→6→10→0,车辆3：0→12→11→15→13→14→0,总花费(总时间与惩罚成本之和)为117.266 6。从结果可以看出,改进的SSA算法在求解文中模型时可以得出更优的解,进一步验证了改进算法的有效性。

图5 规划路径对比图

4 结束语

针对城市间冷链物流的高时效要求,建立了带时间窗的城市间冷链物流的数学模型。针对这个模型,提出了一种改进的离散麻雀搜索算法,通过引入基于维度的邻域学习策略和动态因子更新公式提高麻雀搜索算法的收敛速度和收敛精度,并且通过实验验证了改进算法的有效性。最后使用小规模数据集可视化对比了改进SSA算法与标准SSA算法的路径规划结果。另外,该算法还有很大的改进空间,今后可以在VRPTW的基础上引入更多的约束条件,例如不同型号冷链物流运输车在时速和最大载重量的差异、动态的超出时间窗惩罚因子等,以提升模型的应用广度。