基于改进群稀疏正则化的稀疏角度图像重建

魏志晴,郑文康,白艳萍,谭秀辉,程 蓉,胡红萍,王 鹏

(中北大学 数学学院,山西 太原 030051)

0 引 言

传统计算机断层成像算法可分为解析法和迭代法。解析法由于投影数据等角度间隔缺失,重建图像中会引入条纹状伪影[1],且图像细节严重模糊,重建图像的噪声较大,无法应用于实际诊断。迭代法可以将先验信息融合到重建图像过程当中,具有较好的重建效果。断层成像中应用最广泛的迭代算法是代数重建技术(Algebraic Reconstruction Technique,ART)、联合代数重建技术(Simultaneous Algebraic Reconstruction Technique,SART)和期望最大化(Expectation Maximization,EM)。稀疏角度背景下,一般选取迭代重建法进行图像重建。近年来随着压缩感知理论的提出,基于稀疏先验的正则化方法得到广泛关注,目前已经成为主流[2]。其核心思想是利用重建图像的稀疏先验信息来提高CT图像重建质量,在解决稀疏角度问题中获得了较好的效果。主要包括基于局部平滑的方法、基于字典的正则化方法和基于非局部相似的方法。

基于局部平滑的方法,主要是利用全变分(Total Variation,TV)模型对图像进行局部平滑。Candes等人[3]最先提出了TV正则化模型,此模型在图像处理等领域可以有效抑制噪声并保留图像的边缘、纹理等。Sidky等人[4]在Candes等人的研究成果上,设计了基于约束TV最小化的CT图像重建模型,在稀疏角度采样背景下获得了较好的重建效果。但是TV正则化方法对于具有更多图像纹理细节和复杂边缘结构的图像,会使得重建的图像过度平滑,导致部分细节丢失。

基于字典的正则化方法,如离散余弦变换等,其单一基函数无法满足图像信号的自适应稀疏表示,因此在此基础上出现了许多改进方法。Chen等人[2]提出了一种基于TV与字典学习方法的磁共振成像算法,在保持精细结构方面具有比较好的效果,进一步提高了重建图像质量。Fan[5]提出了基于双字典的稀疏角度MRI图像重建方法,不仅提升了图像质量,而且收敛速度更快。但字典正则项的选取对重建图像的质量起到决定性作用,若选取不当,易造成某些特征被过度惩罚,不能保留微小的特征,使图像细节模糊。

基于非局部相似方法主要是挖掘图像在纹理等结构信息具有重复性的特性。Buades等人[6]提出了著名的非局部均值(Nonlocal Mean,NLM)滤波算法。Huang[7]将NLM算法应用在CT图像ART算法的重建上,得到了较好的效果。崔树辉[8]将BM3D (Block Matching and 3D collaborative filtering)加入到ART算法中,在稀疏角度情况下依旧取得了较高分辨率。Zhang[9]提出了群稀疏表示正则化(Group-Sparse Regularization,GSR)算法,具有良好的捕捉图像奇异性的优良特性,且单幅图像中的稀疏性和非局部相似性是同时存在的,可以很好地达到对稀疏角度下SART重建图像去除伪影的目的。

为了在平滑图像的同时保留不同层次的结构,Zhang等人[10]提出一种用于保持边缘的滤波器,即滚动引导滤波(Rolling Guidance Filter,RGF)。裴佩佩等人[11]将RGF与卷积稀疏表示相结合,应用在图像处理中,克服了边缘模糊,保留了对比度和边缘纹理信息。

受上述研究的启发,该文提出了一种稀疏角度下基于滚动引导滤波和群稀疏表示正则化的SART重建算法,称为SART-GSR-RGF。该算法首先对稀疏角度采样下的图像进行FBP重建,作为SART算法的初始图像;然后采用SART算法进行重建,再经过群稀疏正则化处理;最后采用滚动引导滤波提升图像的对比度,将所得图像再次作为SART重建算法的输入,继续迭代重建,直到得到分辨率较高的图像。这样既利用了GSR的保护边缘和平滑图像的特点,又利用了RGF保留不同层次结构同时传递图像特征的特点。经过实验验证,所提算法对于图像分辨率的提升具有很大作用。

1 理论依据

1.1 FBP重建和SART重建

FBP(Filtered Back-Projection)重建算法的依据是中心切片定理[12]。即空域进行投影得到的一维傅里叶变换,是空域进行二维傅里叶变换的一个切片。通过取遍所有投影值,再进行傅里叶反变换得到空间域分布的图像,就可以得到二维函数。FBP公式表示如下[13]：

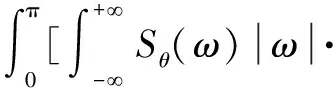
(1)

上述公式表明,重建图像f(x,y)在某一位置的值,是通过该点的所有滤波投影采样的叠加。流程可以简化为图1。

图1 FBP重建示意图

SART算法[14]是CT图像重建中的一类迭代重建算法,在ART和SIRT算法的基础上,进行一次更新只用到了一个投影采样角度下的投影数据,也即该投影角度下所对应的系统方程。在修正某个像素值之前,需要计算一下经过像素的所有射线的误差,以对像素进行修正,并进行加权和归一化处理,再把上述的结果更新到该像素上去。重复此过程,直至满足收敛条件。算法公式为：

(2)

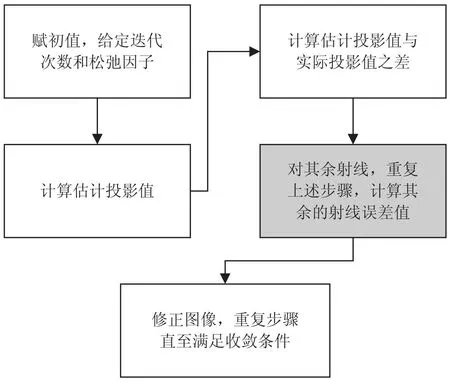
图2 SART算法示意图

其中灰色区域部分即为SART、SIRT和ART算法步骤中变化的部分。就图像重建处理时间而言,解析法比迭代算法具有更好的性能。就降噪和有限数据而言,迭代法优于解析法,因此该文先用FBP对平行透射数据进行成像,之后作为SART迭代重建图像的初值。

1.2 基于群的SR建模

图像处理的稀疏表示(Sparse Representations,SR)就是将图像信号变换到另一个变换域中,绝大部分变换系数的绝对值很小,所得到的变换向量是稀疏的或者近似稀疏的,可以将其作为图像的简洁表达。SR模型可以表示为：

(3)

其中,x表示观测到的信号向量,D是字典,α表示信号的系数,λ是正则化参数,‖·‖0表示l0范数。SR的目标是为训练好的D寻找一个稀疏向量α来表示x。为了更好地用α表示x,必须选择一个有效的字典D。已经提出了一些近似算法来交替优化D和α,如MOD,k-SVD和在线学习。

1.3 滚动引导滤波

滚动引导滤波器具有尺度感知和边缘恢复的优良特性[15],能够保留图像边缘,有效避免模糊现象。RGF首先对物体的尺度进行了筛选,小尺度图像信息主要指的是细节、纹理、小物体和一些噪声。大尺度图像信息主要指的是边界、颜色过渡和变化不明显的区域。小尺度的边缘被平滑掉,仅仅保留了大尺度物体的边缘。大多数边缘保持滤波器没有考虑到在滤波器设计中融入尺度,不能很好地实现小结构与大结构之间的分离。因此,RGF对于双边滤波和非线性扩散滤波具有很大优势,可以用来解决伪影噪声问题。

2 SART-GSR-RGF算法

受群稀疏正则化图像重建[16]研究的启发,该文提出一种基于群稀疏性正则化与滚动引导滤波算法相结合的SART-GSR-RGF重建方法。

图3 相似群构造示意图

GSR算法对每个相似群fGk寻找合适的稀疏字典DG,在确定稀疏字典后,

(4)

其中,αG称为结构GSR,在GSR算法中把αG作为正则项,则求解GSR的无约束优化模型为：

(5)

此正则化模型利用文献[9]来求解。

最后,利用具有尺度感知和边缘恢复的优良特性的RGF进行处理,先要进行小结构去除。

当用小尺度的高斯滤波去除小结构的边缘时,会使得图像边缘被严重模糊。相反,当经过相同方式用同样尺度的高斯滤波去除大结构的边缘时,只是达到了模糊的效果,仍能复原出为视觉所能接受的图像。利用加权平均的形式来表示高斯滤波器算子,可得到：

(6)

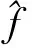
其次进行边缘恢复。在双边滤波器基础上将Ft作为引导图像,迭代过程如式7所示：

(7)

算法1：SART-GSR-RGF

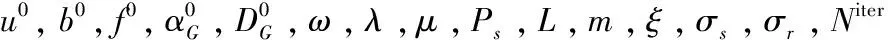
重复

SART重建：

forp=1,2,…,P

ifp=1

up=SART(u0,ω)

else

up=SART(up-1,ω)

end if

end for

ifup<0

up=0,u=up

GSR正则化：

fort=0,1,…,T

updateft+1,et+1=ft+1-bt

for eachfGk

end for

end for

u0=RGF(DG*αG)

满足条件时停止

3 实验结果

本节将对提出算法的重建性能进行验证,测试平台如下：64位Intel Core i7-10700处理器,主机频率2.90 GHz,8G运行内存的Windows10操作系统,数学软件为Matlab R2021a。实验所用模型为Shepp-Logan。在比较不同算法的重建性能之前,首先利用所提算法进行消融实验,即对SART算法、SART-GSR算法SART-RGF算法以及所提算法进行对比分析。同时验证了在不同稀疏角度下各算法的性能,观察重建效果。图4和图5展示了在256个换能器背景下32角度和64角度时不同算法的重建效果;图6和图7展示了在512换能器背景下32角度和64角度时不同算法的重建效果,相对应地也展示了同一放大部分的重建结果。

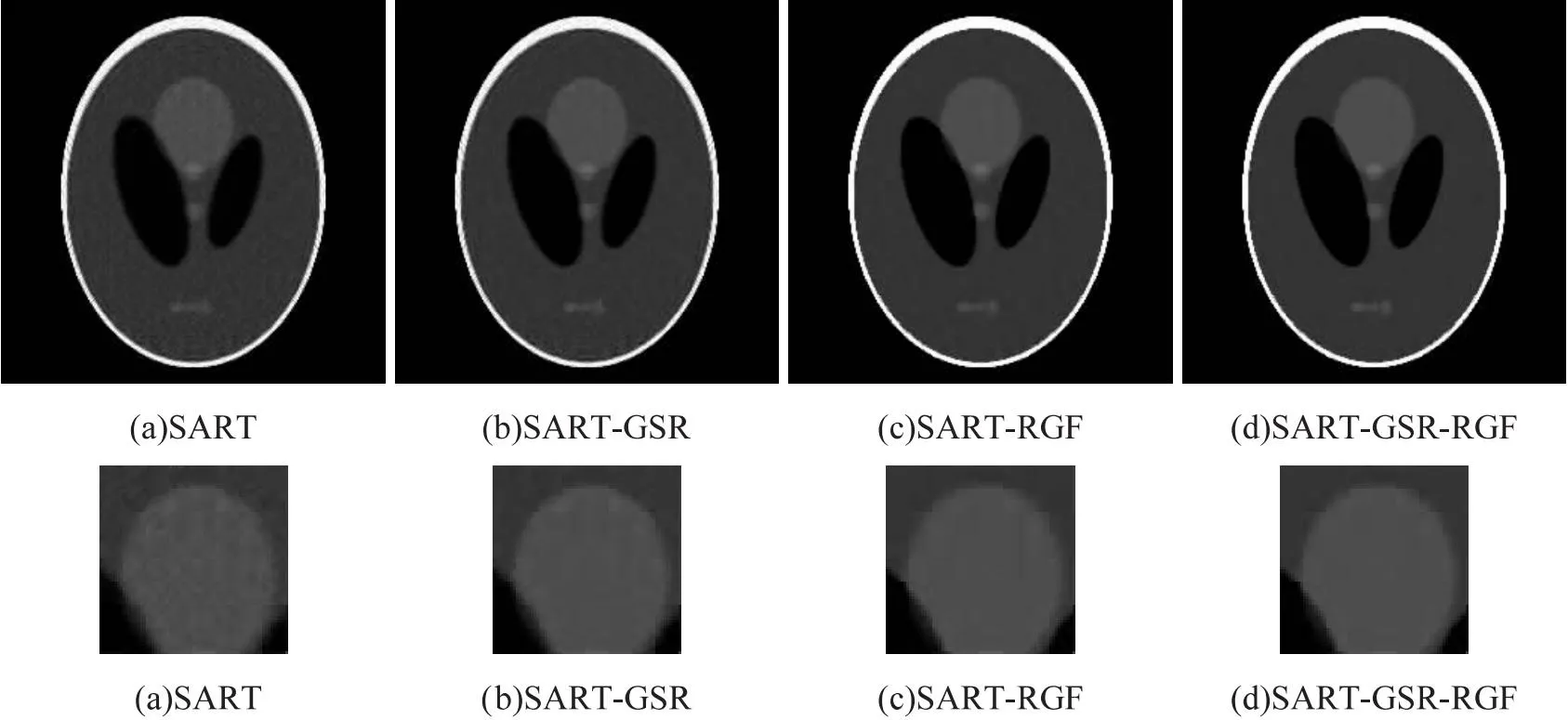
图4 256换能器32角度下图像重建效果比较

图5 256换能器64角度下图像重建效果比较

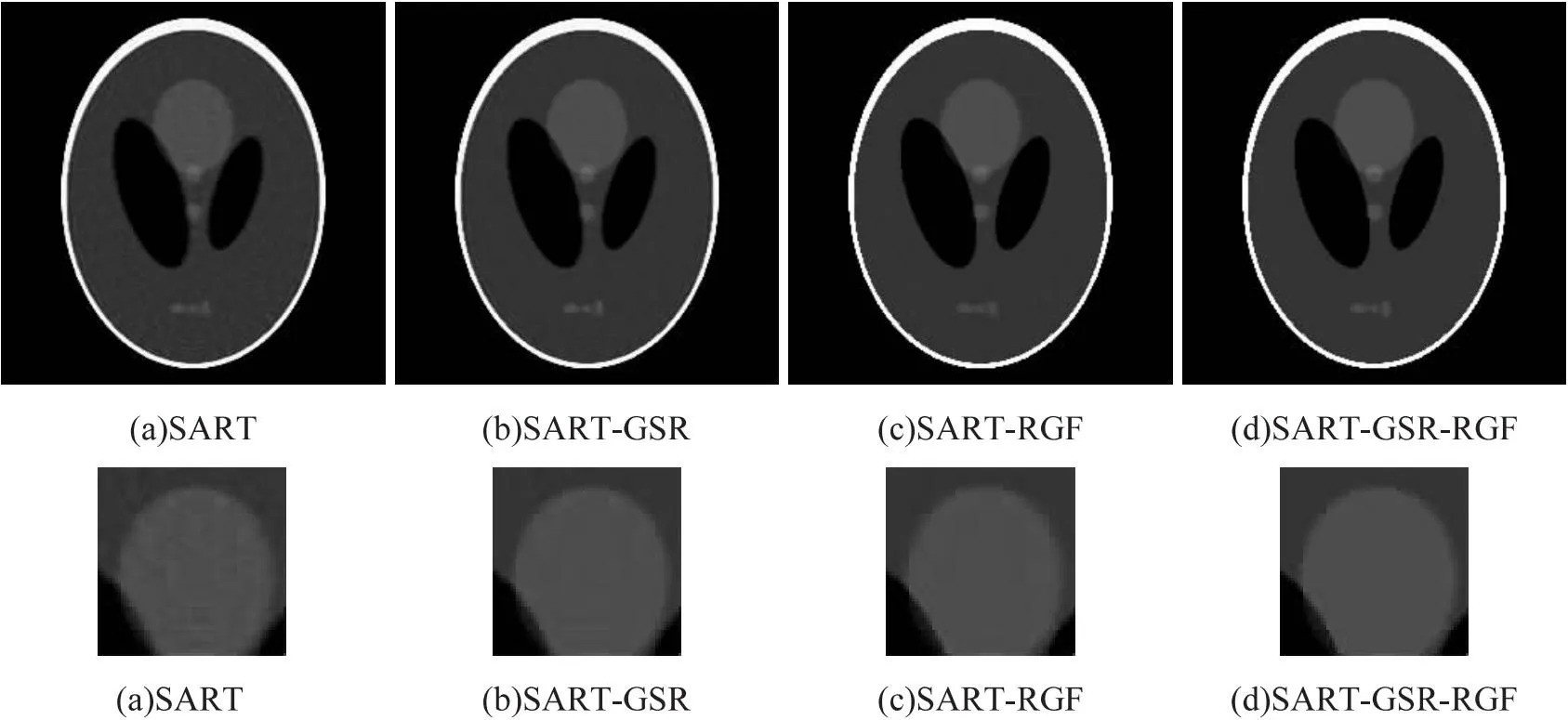
图6 512换能器32角度下图像重建效果比较

图7 512换能器64角度下图像重建效果比较

通过图4至图7可以看出,所提算法具有较好的重建效果,但仅通过视觉效果进行评估算法的重建效果时,评估结果具有一定的主观性。为了更客观地评价所提算法的有效性,使用具体的评价指标进行评价。选择PSNR[17],MSE以及FSIM进行客观评价,其中图8、图10和图12展示了256换能器设置下32/64稀疏角度的20次迭代过程中的PSNR值、MSE值和FSIM值的比较结果及趋势;图9、图11和图13展示了512换能器设置下32/64稀疏角度的20次迭代过程中的PSNR值、MSE值和FSIM值的比较结果及趋势。

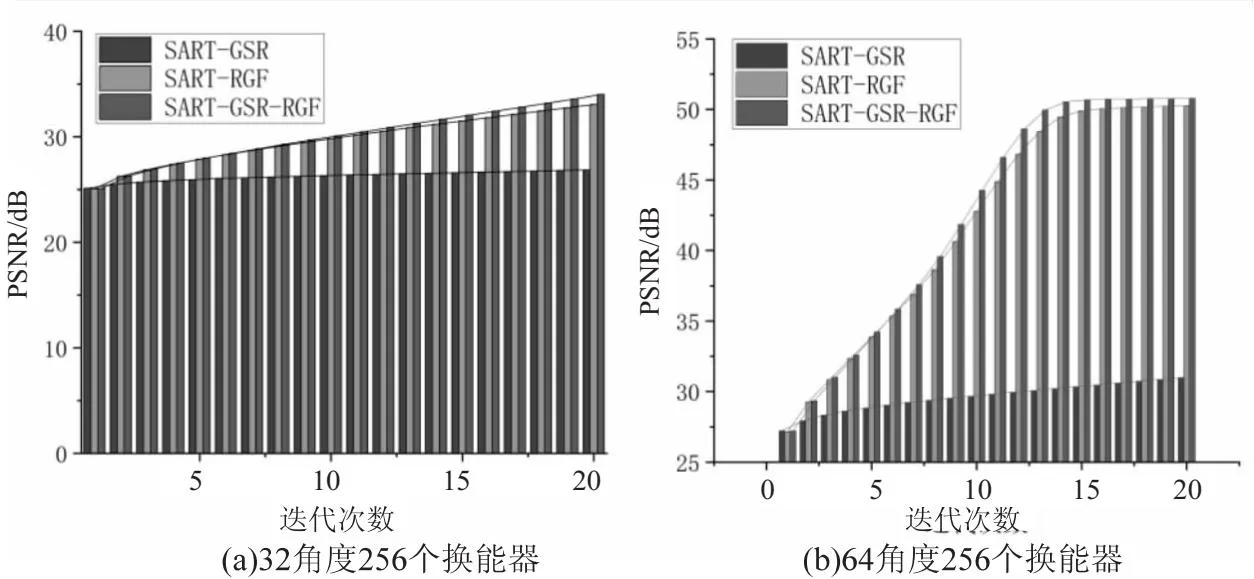
图8 256换能器图像重建效果PSNR比较

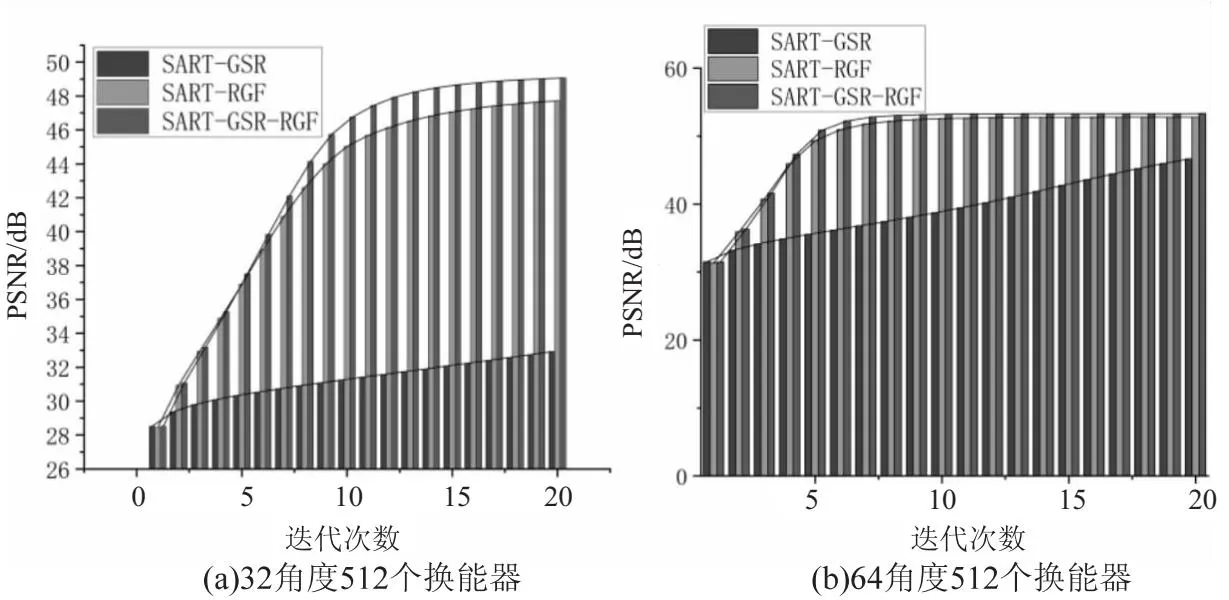
图9 512换能器图像重建效果PSNR比较

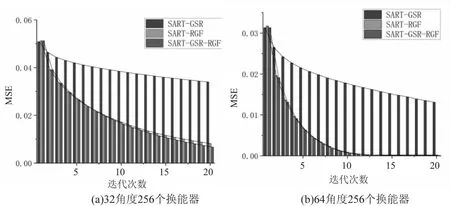
图10 256换能器图像重建效果MSE比较

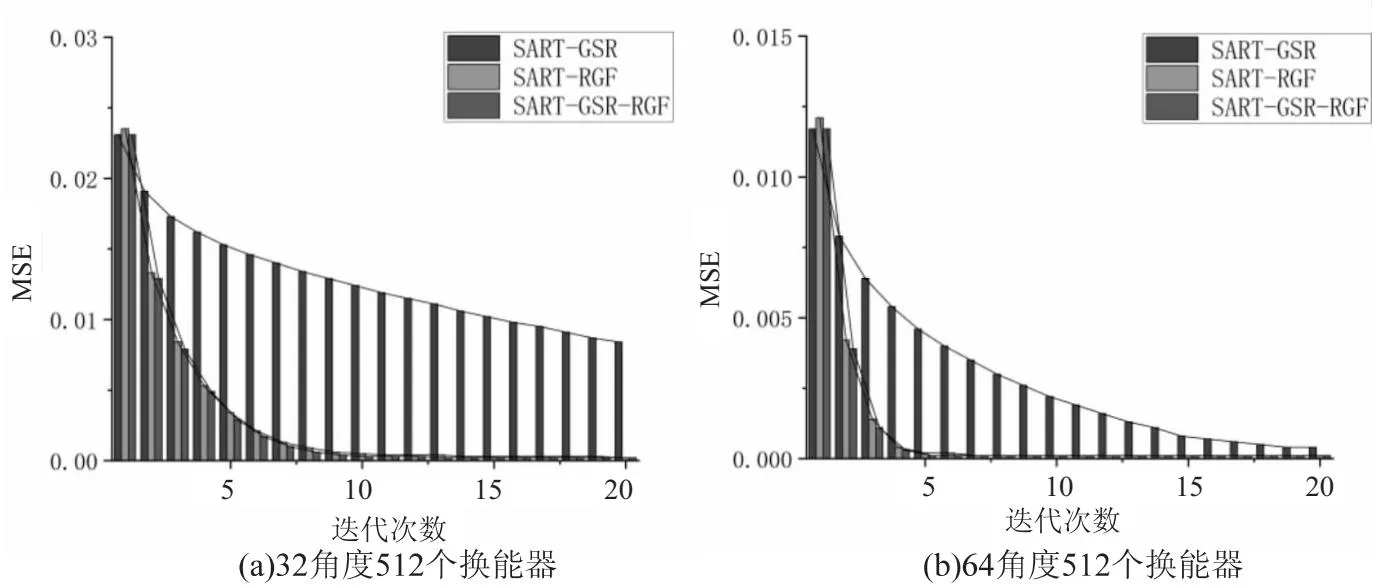
图11 512换能器图像重建效果MSE比较

图12 256换能器图像重建效果FSIM比较

图13 512换能器图像重建效果FSIM比较

根据图8至图13可以很清晰地看到,所提算法SART-GSR-RGF具有最高的PSNR值和FSIM值,以及最低的MSE值。其中PSNR值越大,意味着图像重建后的保真效果越好,图像越清晰;FSIM值越高,意味着当前所测试的图像越接近参考图像;MSE值越小,意味着与原始重建图像相差越低,具有较好的重建性能。并且从图中可以看到,所提算法在迭代开始前期就已经达到了比较好的性能,说明所提算法具有很好的收敛性能,即算法收敛速度快。

为比较各类方法的优劣性,验证所提算法的有效性,表1给出了SART算法、TV-POCS算法、SART-NLM算法以及SART-GSR-RGF算法的PSNR,RMSE以及FSIM的数据。结果表明,所提算法在重建结果上均优于其他4个对比算法。

表1 不同算法重建性能比较

4 结束语

该文提出了一种稀疏角度下基于滚动引导滤波和群稀疏表示正则化的SART重建算法,称为SART-GSR-RGF。由于群稀疏正则化在去掉伪影的同时,可能将边缘或细节过度平滑,使得对比度降低,无法获得符合人类视觉效果的高分辨率图像,因此利用滚动引导滤波进行一定的对比度提升,再次作为SART的输入进行迭代。经过算法的分析以及实验的验证表明,所提算法具有良好的重建效果。接下来,将对此算法进行进一步研究,以期获得三维头骨模型的较高质量的重建。