可变风险溢价结构下跳扩散模型的期权定价

朱福敏 周海川 郑尊信

(深圳大学经济学院，广东 深圳 518060)

一、引言

期权作为重要的金融衍生工具，在投资者的资产配置与风险管理中起着重要作用。2015年2月9日，上证50ETF期权作为我国首只场内期权在上交所上市，标志着期权时代的开启。我国期权市场虽然起步较晚，但正处于高速发展阶段。2017年4月19日，白糖期权于郑商所上市；2018年9月，我国首只工业品商品期权——铜期权于上期所上市；2019年12月23日，沪深300ETF期权于上交所、深交所上市，产品日趋完善。期权的合理定价对于促进我国期权市场健康发展，维护金融市场稳健运行具有重要意义。

早在1973年，Black and Scholes(1973)便提出了经典的BS期权定价模型。该模型假设标的资产价格服从几何布朗运动，且市场是完备的，即任何衍生证券都能被完美复制，从而得到了期权定价的封闭解析式。在完备市场的假设条件下，BS模型具有唯一的风险溢价结构。然而，该模型的基本假设与市场中呈现的尖峰、厚尾和有偏特征明显不符。事实上，由于交易费用与交易限制等市场摩擦的存在，衍生证券无法被完美复制，导致市场不是完备的。为此，Merton(1976)在此基础上引入复合泊松跳过程，建立了跳扩散模型。Harrison and Pliska(1981)指出存在跳跃的市场也是不完备的，此时风险无法被完美对冲。在此之后，大量带跳跃的不完备市场模型被陆续提出，逐步取代完美市场假设下的BS模型(Duffie et al.，2000；Carr et al.2002；Christoffersen et al.，2012；Ornthanalai，2014；Aït-Sahalia et al.，2015；朱福敏等，2018)。

值得注意的是，不完备市场中定价核与等价鞅测度不再唯一，即存在非唯一的风险溢价结构。跳扩散模型同时包含了扩散与跳跃两种风险，根据投资者偏好的不同，风险的市场价格会随之变化，模型具有多种可能的理论期权价格。因此，如何选取合适的定价核进行测度变换，并确定合理的风险溢价结构，是解决不完备市场跳扩散模型期权定价的关键。目前不完备市场模型下的测度变换方法主要有方差最优鞅测度(Schweizer，1996)，最小熵鞅测度(Miyahara，1996、2011)以及Esscher变换法(Gerber and Shiu，1994；Bühlmann et al.，1998；Bakshi et al.，2003；Carr and Wu，2004)等。然而，上述方法通常提前对投资者的风险偏好做出假定，仅根据真实测度的溢价信息便确定了等价鞅测度，忽视了跳跃风险在衍生品市场中的功能和作用，难以刻画风险的真实市场价格，导致无法准确地进行期权定价。

为了考察市场中投资者对于不同风险的溢价补偿需求，探究市场风险定价机制，提升模型期权定价效果，本文选择跳扩散这一经典的不完备市场模型作为理论框架，参考Christoffersen et al.(2012)、朱福敏等(2018)的离散时间模型，在单变量Esscher方法的基础上将两种风险因子分离，借助具有自由度的定价核，赋予跳跃风险不同于扩散风险的溢价补偿机制，尝试构建合适的风险溢价结构。该结构于理论层面赋予了模型更灵活的风险溢价刻画能力，同时允许使用期权市场数据对不同风险的市场价格进行校准，进而提升模型定价效果。在可变风险溢价结构外，本文还选取两种特殊风险溢价结构作为对比：一是Merton提出的不含跳跃风险溢价的情形，此时跳跃风险作为可分散风险未被定价；二是单变量Esscher对应的风险结构，此时跳跃风险与扩散风险具有相同的溢价补偿机制。结合模型的数值分析结果表明，可变风险溢价结构能够刻画更为陡峭的定价核曲线，以及具有更厚左尾的风险中性分布。

本文对上证50ETF期权、华泰柏瑞沪深300ETF期权以及标普500指数期权开展研究，使用2016―2020年标的价格数据估计模型参数，借助2021年1月4日至2月19日的期权数据估计每日风险溢价结构。对风险溢价结构与定价核的分析结果显示，可变风险溢价结构下跳跃风险溢价的占比更高，并且跳跃风险溢价具有明显的时变特征，其与日均隐含波动率水平间存在较强的正相关性，能够较好地解释期权市场中的隐含波动率曲面。可变风险溢价结构对应的定价核曲线也更为陡峭，更能准确刻画市场隐含定价核形状与投资者偏好。此外，其在样本内与样本外也具有更好的定价效果。

本文进一步从样本长度、定价方法、定价区间以及期权产品四个方面对结论的稳健性进行了检验：其一，分别使用2年、4年、6年、8年以及10年的标的样本，排除样本长度对模型参数估计带来的影响；其二，分别使用蒙特卡洛模拟法(Boyle，1977)、快速傅里叶变换法(Carr and Madan，1999)、格方法(Fu et al.，2017)以及有限差分法(Cont and Voltchkova，2005)四种数值方法，排除定价方法带来的影响；其三，分别使用以2021年6月1日与11月1日为起点的30日期权样本，和以2022年1月4日与9月1日为起点的60日期权样本，排除定价区间带来的影响；其四，增加华泰柏瑞沪深300ETF期权与标普500指数期权，排除期权产品带来的影响。研究结果表明，可变风险溢价结构的定价优越性是稳健的。

本文主要创新如下：一是使用双变量形式的定价核为跳扩散模型构建了含有自由度的可变风险溢价结构，相较于传统测度变换手段，其能够通过市场隐含的风险偏好信息校准模型中不同风险的市场价格，于理论层面提升了模型的定价能力。二是通过对上证50ETF期权的实证分析发现，跳跃风险溢价在风险溢价中占据主导，并且具有明显的时变特征，其与期权隐含波动率之间存在较强的正相关性，能够较好地解释隐含波动率曲面。此外，本文发现可变风险溢价结构能够更准确地刻画市场隐含定价核曲线，且具有更精确的期权定价能力，揭示了跳跃风险溢价的重要作用。

二、模型和风险溢价结构

(一)跳扩散模型

本文使用Merton(1976)所提出的跳扩散模型刻画标的资产的价格动态。假设价格St在概率空间(Ω, , )上服从如下的指数Levy过程：

其中，σ为扩散波动率，Jt为用于捕捉资产价格跳跃的复合泊松过程：

该过程一方面通过强度为λ的泊松过程Nt描绘跳跃事件发生的时机，另一方面通过独立同分布的随机变量Yj刻画跳跃幅度大小。在漂移项中使用补偿项ψ(1)进行凸度修正，使下式成立：

其中，ψ(∙)为跳跃项Jt的矩母指数：

从而μ可代表标的资产的期望收益率，其与波动率σ以及跳跃强度λ均为非时变参数。

跳跃项的引入使得跳扩散模型能够刻画出非高斯的市场收益率分布与非平坦的隐含波动率曲面。该模型较好地平衡了现实性与易处理性，具有一定的应用价值。为便于实现模型价格计算与参数估计，本文选择使用正态跳扩散模型。具体而言，跳跃幅度Yj服从均值为μJ，方差为的正态分布。借助Levy-Khinchin定理可得跳跃项矩母指数的具体表达式：

将漂移项中跳跃项的凸度修正项ψ(1)记为λk，其中：

跳跃幅度分布的正态假定易于推导对数似然函数和期权理论价格解析解，简化了参数估计与期权定价过程，有利于探究市场风险的定价机制。

(二)可变风险溢价结构

为避免预先对风险溢价结构作出假定，本文参考Christoffersen et al.(2012)、朱福敏等(2018)在离散模型下的思路，在定价核中将扩散风险与跳跃风险分离，使得风险溢价结构相较于Bates(1991，2006，2008)以及Zhang et al.(2012)等传统结构具有了额外自由度，允许期权数据参与校准风险市场价格。具体而言，令等价测度 在t时刻下对于真实测度 的Radon-Nikodym导数具有如下形式：

其中，θw与θJ分别控制扩散与跳跃两种随机风险因子。通过比较对数价格过程Xt在两种测度下的矩母指数，即可得到两测度间参数的对应关系：

其中，*代表 测度下的相关参数。1若要使得 成为等价鞅测度，则还应同时满足如下的风险中性约束：

此时意味着 测度下的期望收益率μ*应当与无风险收益率r相等，则(10)式等价于：

通过简单的代数变换即可得到风险溢价结构：

其中，(12)式左侧为风险溢价，右侧可视为对风险溢价的分解，由于ψ(u)中包含跳过程Jt的信息，故将[ψ(1)-ψ(1-θJ)+ψ(-θJ)]整体视为跳跃风险溢价，同时将σθw视为扩散风险溢价。其中θw与θJ分别控制着两种风险溢价的大小，构成了可变风险溢价结构。此时可将θJ视为风险溢价结构中的自由度，θw通过(13)式被θJ唯一确定：

若将波动率σ与跳跃强度λ分别视作扩散风险与跳跃风险的测度，则两种风险所对应的市场价格分别为θw和[ψ(1)-ψ(1-θJ)+ψ(-θJ)]/λ。借助Gerber and Shiu(1994)的结果可知，扩散风险溢价与跳跃风险溢价分别对于θw和θJ单调递增，从而定价核自由度θJ的增加会使得跳跃风险溢价上升，当风险溢价总和给定时，扩散风险的溢价水平会随之降低，θw也会对应减少。因此，参数θJ与风险溢价结构之间存在一一对应关系，且定价核参数θJ的大小可以反映出跳跃风险的相对占比。在实际使用中，基于给定的真实测度分布，可以利用期权市场的额外信息对定价核参数θJ进行校准，识别出符合市场的风险溢价结构。

考虑正态假定下的跳扩散模型，跳过程中的参数变换关系如下：

其对应的风险溢价结构为：

上述可变风险溢价结构随着定价核参数θJ的变化，可以灵活刻画投资者不同种类的风险偏好，包含以下两种特殊风险溢价结构：第一种是定价核参数θJ为零的情形，对应Merton(1976)所采用的测度变换方式，其风险中性测度下的跳过程参数与真实测度下一致，即不存在跳跃风险溢价，总溢价全部由扩散风险溢价构成。此时跳跃风险被假设为可分散的非系统风险且未被定价(杨智元和陈浪南，2001)，忽视了跳跃风险的重要贡献(赵华，2012；刘静一等，2015；Pan，2002；Ornthanalai，2014)；第二种则是θw与θJ相等的情形，对应单变量Esscher的变换方式，其将扩散风险与跳跃风险视作整体，二者具有相同的溢价补偿机制。此时方程(12)有且仅有一个解，意味着风险溢价结构被唯一确定，投资者风险偏好无法调整。

三、方法和数值分析

本文首先对使用的参数估计方法与定价方法进行简要介绍，然后对期权理论价格与跳跃风险溢价的影响机制以及不同风险溢价结构的定价核进行数值分析。

(一)参数估计方法

本文使用极大似然法分别借助标的资产与期权信息，实现模型参数与定价核参数的估计。具体而言，使用标的资产收益序列估计出模型参数，在此基础上继续使用期权数据校准定价核参数。在似然函数的构建上参考了Ornthanalai(2014)的做法，下面分别给出针对标的资产与期权的对数似然函数构造方式。

基于标的资产的对数似然函数L的构造方式如下：

其中，p(x)为概率密度函数，进一步借助(2)式以跳跃次数为条件对其进行全概率展开：

借助正态分布的可加性不难得出：

从而每个对数收益率的概率密度可由若干个正态概率密度加权求和得出，在实际使用时需对求和上限加以限制。

基于期权的对数似然函数L的构造方式如下：

IV与IV分别代表市场与模型期权价格对应的隐含波动率，此处假设误差ϵj服从均值为0、方差为的正态分布，σϵ为误差序列的标准差。

(二)定价方法

本文使用的Merton跳扩散模型具有欧式期权价格的解析表达式，能够准确快速计算出期权的理论价格。进一步在稳健性测试中，为排除定价方法的选择对结论带来的影响，还将引入几种数值定价方法，分别为蒙特卡罗模拟法、快速傅里叶变换法、格方法以及有限差分法。其中，蒙特卡罗模拟法通过随机模拟价格变化路径，并借助样本均值近似求解，其适用范围广，但耗时较长且结果具有波动性；快速傅里叶变换法利用离散求和近似求解积分，其计算效率高但仅适用于存在特征函数的随机过程；格方法能够在价格时间均为离散的框架下给出封闭的期权价格数值解，其计算复杂度适中且适合应用在跳扩散模型中；有限差分法则对期权价格所满足的偏微分方程进行差分近似，使用反向递归算法求解，其使用限制较少且结果稳定。2

(三)数值分析

一方面，通过理论分析可知跳跃风险溢价与定价核参数θJ间存在着正比关系3，而定价核参数θJ会直接影响风险中性测度参数，进一步影响期权的理论价格。其中θJ对跳跃强度λ*与跳跃幅度均值μ*J的影响机制较为明晰，不难发现μ*J是关于θJ单调递减的线性函数，λ*的指数部分是关于θJ的二次函数。但风险中性测度参数与期权价格间存在高度非线性关系，需要借助数值模拟方法进行分析。另一方面，不同的风险溢价结构下，风险中性测度参数不同，从而对应的风险中性分布与定价核曲线也存在差异，借助数值分析可以进一步理解跳跃风险溢价对于投资者偏好与定价核的影响。

本文首先考察跳跃风险溢价对理论期权价格的影响机制，分析跳跃强度λ*与跳跃幅度均值μ*J对期权理论价格的影响，进一步分析跳跃风险溢价对其的影响机制。

图1展示了不同价值程度下参数对看涨期权与看跌期权理论价格的影响。分析结果表明，随着跳跃强度的增加，期权的理论价格也随之上涨，但跳跃幅度均值对理论期权价格的影响则呈U型关系。为进一步考察定价核参数变化对期权理论价格带来的综合影响，并直观展现跳跃风险溢价与期权价格之间的联系，图2给出了不同价值程度下看涨看跌期权关于跳跃风险溢价的变化。在该组参数设定下，随着跳跃风险溢价的增加，期权的理论价格亦会增加，且增速会伴随跳跃风险溢价水平的升高而提升。

图1 理论期权价格关于风险中性测度参数变化

图2 理论期权价格关于跳跃风险溢价变化

然后考察不同的风险溢价结构(Merton、Esscher、可变)，比较其风险中性分布与定价核曲线的差异。图3绘制了不同风险溢价结构下的风险中性概率分布。结果表明，相较于两种特殊结构，可变风险溢价结构对应的分布与真实测度差距更大，具有更厚的左尾，提升了损失情形下的预期。

图3 日度对数收益率分布比较

依据上述结果，进一步可以绘制出三种风险溢价结构对应的定价核曲线，结果展现在图4中。其中定价核计算方式如下：

图4 三种风险溢价结构下定价核曲线

由于(8)式中Radon-Nikodym导数具有指数形式，故定价核具有单调递减的特征。又因Merton与单变量Esscher所对应的风险中性测度与真实测度差距较小，从而定价核曲线较为平坦。相较而言，可变风险溢价结构校准出的定价核则更为陡峭，表明在定价时投资者对于未来所可能遭受的损失赋予了更高的权重，同时对于正向收益的权重有所降低。

四、数据和实证分析

(一)数据选取

上证50ETF期权采取以竞价交易为主、做市商为辅的T+0交易模式，自上市以来就受到投资者的广泛关注。根据上海证券交易所提供的统计数据，上证50ETF期权于2015年2月共成交232508张，8年以来市场在不断地发展并趋向成熟，2023年10月的成交量共计30115412张，成交额高达1042970万元。作为我国首只场内期权，上证50ETF期权发展时间相对较长，市场参与者较为广泛，数据量较为充足，为参数估计、模型校准以及定价检验等提供了较好的基础，故本文将其作为实证研究主体。

考虑到样本量的充足性，基于相关研究工作(孙有发等，2018；吴鑫育等，2019；孙有发等，2020)，本文选取2021年1月4日至2021年2月19日共30个连续交易日的期权价格数据，标的层面对应选取2016年1月4日至2020年12月31日的收盘价数据，使用隔夜上海银行间同业拆放利率(SHIBOR)作为无风险利率，以上数据均来自Wind数据库。为排除期权产品带来的影响，本文同样使用了华泰柏瑞沪深300ETF期权以及标普500指数期权进行稳健性检验，数据分别来自Wind数据库与Option Metrics数据库。

图5给出了2006年1月4日至2022年12月31日的上证50ETF对数收益率，表1为相应描述性统计结果。结果显示，上证50ETF对数收益率呈现明显的负偏度与超额峰度的特征，从而使用Merton跳扩散这类不完备市场模型具有重要性与必要性。

表1 上证50ETF对数收益率的描述性统计结果

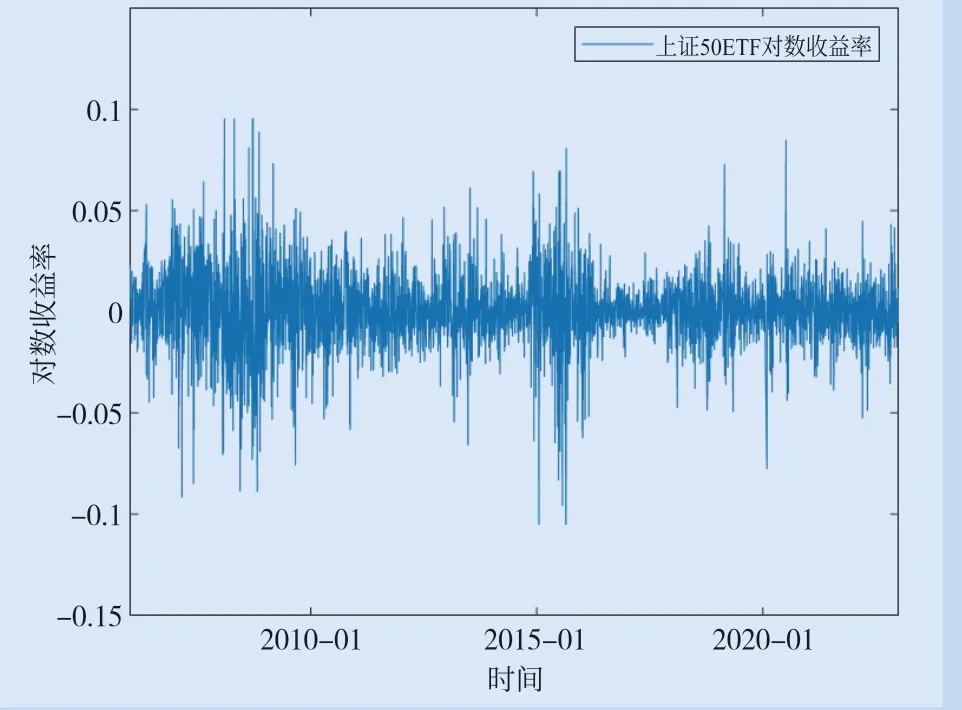
图5 上证50ETF对数收益率(2006―2022)

为保证期权数据的有效性，本文剔除了所有不满足无套利条件以及价格不足0.01元的期权，保留了到期期限在7个交易日与100个交易日之间，且价值程度(执行价格与初始标的价格之比)处于0.9与1.1之间的期权，并按照不同的到期期限与价值程度分成9个类别。到期期限方面，以30个交易日与60个交易日为界分为三类；价值程度方面，当价值程度小于0.97时，看涨(看跌)期权为实值(虚值)期权，当价值程度大于等于0.97且小于1.03时为平值期权，当价值程度大于等于1.03时，看涨(看跌)期权为虚值(实值)期权。经筛选后共计得到1726个期权数据，其中包含873个看涨期权与853个看跌期权，平均每个交易日约有57个期权数据。表2给出了所选期权的描述性统计结果。

表2 上证50ETF期权的描述性统计结果

(二)参数估计结果

对于真实测度下的模型参数，本文使用2016年1月4日至2020年12月31日的上证50ETF对数收益率序列进行估计。在本文所提出的可变风险溢价结构之外，还将考虑前文中所提及的两种特殊风险结构，此二者的定价核参数θJ由真实测度模型参数与无风险利率确定。对于可变风险溢价结构，根据估计出的真实测度参数，使用2021年1月4日至2021年2月19日的每个期权交易日的期权价格数据估计该日的定价核参数θJ。

基于参数估计结果，本文选取2021年1月18日作为代表性交易日，当日三种不同风险溢价结构所对应的参数估计结果如表3所示。其中Panel A为真实测度下的模型参数，Panel B为不同风险溢价结构的定价核参数与对应风险中性测度下的模型参数。估计结果表明，所选时段内上证50ETF价格的跳跃强度为0.7282，跳跃发生较为频繁。Panel B中两种特殊风险溢价结构所对应的定价核参数θJ较小，使得对应风险中性测度参数改变不大。而可变风险溢价结构下的风险中性跳跃强度上升至0.799，跳跃风险溢价占比有了显著提升。

表3 参数(日度)估计结果

为考察几种风险溢价结构下的定价核与市场中真实定价核曲线的差异，本文参考Almeida and Freire(2022)的做法，使用非参数方法绘制该日上证50ETF期权的隐含定价核，并与三种风险溢价结构下的模型定价核进行比较。该方法借助标的资产历史收益率所构成的经验分布与市场中单只期权计算出市场隐含定价核曲线。4此处依据到期期限与价值程度选取了2021年1月18日具有代表性的四只期权，相应定价核曲线如图6所示。

图6 期权隐含定价核与模型定价核比较

图6显示，随着到期期限的增加，期权隐含的定价核曲线会愈发陡峭。相较于市场中的隐含定价核，Merton与单变量Esscher两种风险结构所能提供的定价核过于平坦，而可变风险溢价结构所校准出的定价核曲线则更好地反映出市场中的偏斜特征，表明投资者愿意为损失情形下的阿罗―德布鲁证券支付更高的价格。同时也凸显了可变风险溢价结构的优势，即当传统的测度变换手段无法准确描绘市场中投资者的风险偏好时，其能够利用市场中的真实数据进行校准，从而更好地捕获市场中的隐含信息并进一步提升模型定价能力。

(三)风险溢价结构分析

通过前文关于风险溢价结构的理论分析可知，在给定真实测度模型参数与无风险利率时，定价核参数θJ与跳跃风险溢价水平之间存在着正比关系，从而定价核参数反映了跳跃风险溢价的占比大小。图7分别展示了30个交易日下可变风险溢价结构与单变量Esscher风险溢价结构中定价核参数θJ的折线图。相较于前者，后者的定价核参数处于较低值，而反观可变风险溢价结构下的跳跃风险溢价则具有明显的时变特征；此外，通过引入每个交易日的平均隐含波动率，可以发现两者之间存在较为明显的正相关性。

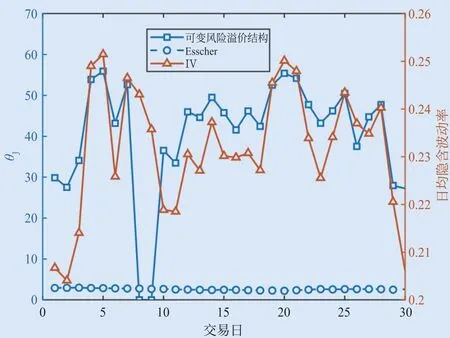
图7 定价核参数与日均隐含波动率折线

为进一步验证上述发现，本文对期权加以细分，分别对实值(ITM)、平值(ATM)、虚值(OTM)下的看涨期权与看跌期权，重新校准出每个交易日下对应的定价核参数θJ，考察其时变特征以及与隐含波动率之间的联系。图8(a)(b)给出了看涨与看跌期权在不同价值程度下所对应跳跃风险溢价水平的时变图，图8(c)(d)则为相应类别下的日均隐含波动率水平。

图8 细分期权下定价核参数与日均隐含波动率折线

通过对比图8(a)(b)与(c)(d)两部分，发现在区分看涨看跌以及价值程度后，跳跃风险溢价占比与隐含波动率仍存在较强的正相关性。此外，为排除期权样本区间选择的特殊性，在原样本基础上延长90个交易日，图9绘制了2021年1月4日至7月2日共120个连续交易日的定价核参数与日均隐含波动率折线图。样本中期的隐含波动率水平较低，使得可变风险溢价结构所校准的定价核参数大量为零；但在样本前期与后期，日均隐含波动率水平较高，跳跃风险溢价占比显著上升，此时二者之间的正相关性较为明显，说明跳跃风险溢价对于隐含波动率具有较强的解释能力。

图9 定价核参数与日均隐含波动率折线(2021.1.4―2021.7.2)

对此，本文给出的可能解释为，当跳跃风险溢价占比更高时，投资者对于跳跃风险具有更高的溢价补偿需求，对市场中极端收益的出现也更为担忧，从而愿意为抵御相关风险支付更高的期权价格，使得市场隐含波动率水平随之上升。此外，上述结果也反映出投资者的风险偏好具有明显的时变特征。若提前对投资者偏好做出假定，则会使不完备市场模型对于风险结构的刻画出现较大偏差，进一步影响模型定价效果。这体现了跳跃风险在定价中的重要作用，以及使用可变风险溢价结构的必要性与重要性。

(四)期权定价结果

前文基于参数估计结果对定价核与风险溢价结构进行了分析，本文进一步对模型的期权定价能力展开研究。表4给出了跳扩散模型下三种风险溢价结构的样本内外总体定价误差，理论期权价格使用解析解计算。

表4 样本内外总体定价误差

其中，样本内指使用定价核参数对当日期权进行定价，样本外则是对次日期权进行定价。为排除期权价格尺度以及隐含波动率水平对误差计算带来的影响，参考Zhu et al.(2020)的做法，本文选择使用隐含波动率的相对均方根误差RMSRE(root mean square relative error)作为定价误差的衡量指标：

研究显示，单变量Esscher情形的样本内外定价误差略低于Merton情形，由于Esscher结构下的定价核参数较小，其定价结果与Merton仅存在微小差距，与前文的相关分析结果一致。而可变风险溢价结构在定价误差层面有了显著降低，其样本内外RMSRE分别为11.88%与12.81%。图10则更为直观地展现了三种风险溢价结构在不同价值程度与到期期限下的样本内与样本外RMSRE折线图。结果表明，无论是样本内还是样本外，可变风险溢价结构都具有更优越的定价能力。为展示更加详细的定价结果，在表5中给出了不同到期期限与价值程度下看涨与看跌期权在样本内与样本外的定价误差。

表5 样本内外详细定价误差

图10 期权定价误差折线

研究表明，在执行价格较高的期权中(虚值看涨与实值看跌)，Merton情形下的定价效果要略优于Esscher情形，而可变风险溢价结构则一直具有更低的定价误差，且改善效果明显。上述结果表明，Merton与Esscher所代表的单一风险溢价结构的定价效果只依赖于模型参数的估计结果，无法根据期权市场信息进行调整；而可变风险溢价结构则通过额外的定价核参数识别市场隐含的偏好信息，从而刻画出符合市场的风险结构，进而提升期权定价误差。通过比较不同风险溢价结构在样本外的定价误差可以发现，可变风险溢价结构并未呈现过拟合现象，依然具有显著的定价优势。但同时也注意到，可变风险溢价结构在样本内外的定价误差变化更为明显，这是由于市场中跳跃风险溢价具有强烈的时变特征，从而不同交易日间的定价核参数差异较大，在使用当日参数定价下一日的期权时，其对风险溢价结构的刻画会出现一定的偏差。而在Merton与Esscher情形下，定价核参数不依赖于期权数据，具有较强的稳定性，故其在样本内外的定价结果不存在明显差异。

(五)稳健性检验

为检验可变风险溢价结构下跳扩散模型定价能力的稳健性，本文拟从以下四个方面进行验证：第一，考虑到标的样本长度会对模型参数的估计结果产生影响，在前文所使用的5年期样本之外，还选择2年、4年、6年、8年以及10年期的样本。第二，使用前文介绍的四种数值定价方法代替解析解排除定价方法带来的影响，同时也为其他不存在封闭解的跳扩散模型提供参考。第三，为排除定价区间选择带来的影响，选取以2021年6月1日和11月1日为起点的30交易日区间，同时还考虑更大的定价样本量，选择以2022年1月4日和9月1日为起点的60日交易日区间。第四，使用华泰柏瑞沪深300ETF期权以及标普500指数期权，为可变风险溢价结构的适用性提供更多证据。稳健性检验结果如表6所示，其中定价误差指标依然使用隐含波动率的相对均方根误差。

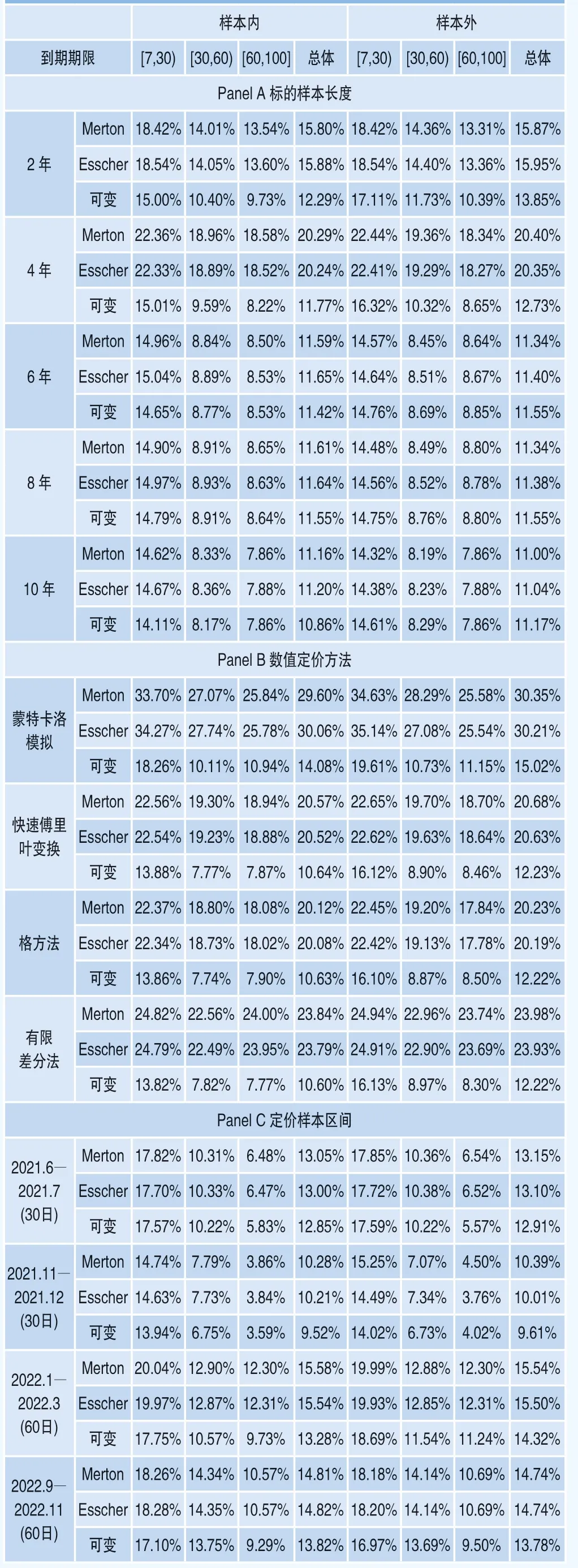
表6 定价误差的稳健性检验

首先，关注Panel A中不同长度标的收益率样本对定价结果的影响。结果表明，在使用较短样本(2年和4年)估计时，可变风险溢价结构的定价误差依然要明显小于其余两种结构，但当使用较长样本(6年、8年和10年)进行估计时，三者之间的定价效果差距不再明显。这从侧面反映了单一风险溢价结构十分依赖真实测度下的模型参数，而可变结构则可以借助期权数据的校准拥有稳定的定价能力。

其次，观察Panel B中四种数值方法的定价结果。相较于其他三种数值方法，蒙特卡洛模拟的整体误差要明显高于解析解。通过比较三种风险溢价结构可以发现，可变风险溢价结构仍具有更低的定价误差。该结果表明，使用数值定价方法同样可以发挥可变风险溢价结构的定价优势，即对于不存在解析解的其他跳扩散模型同样适用。

再次，比较Panel C中不同期权样本定价区间的结果。可以发现，可变风险溢价结构的定价误差仍然更低，但随着定价区间的改变，其误差水平与改善幅度也会变化。由于本文使用的是隐含波动率的相对均方根误差，从而可以对不同定价区间的误差大小进行比较，其中以2021年11月1日为起点的区间上模型整体定价误差最小，而在以2022年1月4日为起点的区间上整体误差最大。

最后，观察Panel D中不同期权产品的定价结果。对于华泰柏瑞沪深300ETF期权，可变风险溢价结构对于定价误差仍有巨大改善，但对于美国标普500指数期权，其改进效果偏弱，并且Esscher方法下的误差要明显高于Merton情形。此外，对于美国市场而言，即使通过风险溢价结构的校准，跳扩散模型的定价误差仍高于20%，由此推测该模型的解释能力可能较弱，可以尝试包含无穷跳与随机波动率的模型。

综上所述，可变风险溢价结构在上述四个层面的检验下依然具有稳定的定价优越性。

五、结论与启示

定价核作为连接真实测度与风险中性测度的桥梁，能够反映投资者的风险偏好信息。然而，在不完备市场模型中，定价核的非唯一性表明仅仅依据真实测度分布无法确定合适的风险溢价结构，因此有必要采取恰当的手段更准确地刻画市场中投资者的风险偏好信息。本文在跳扩散模型的理论框架下，通过分离扩散风险与跳跃风险，为其构建了具有自由度的可变风险溢价结构，允许模型利用额外的期权信息对风险的市场价格进行校准，进而提升模型的期权定价能力。

与此同时，本文对上证50ETF期权、华泰柏瑞沪深300ETF期权以及标普500指数期权开展了数值分析与实证研究，主要结论如下：其一，通过比较不同风险溢价结构下的定价核曲线，发现可变风险溢价结构下的曲线更为陡峭，能够更准确地刻画市场中隐含的定价核形状，投资者对于损失情形下的溢价补偿需求更高。其二，通过分析市场隐含风险溢价结构发现，跳跃风险溢价占比具有明显的时变特征，且与日均隐含波动率之间存在较强的正相关关系，该现象在细分期权市场以及考虑更长时段之后依旧存在，表明跳跃风险溢价对于市场隐含波动率曲面具有解释作用。由于较高的跳跃风险溢价占比表示投资者更加厌恶极端收益的出现，从而其为抵御相关风险愿意支付更高的期权价格，提升了隐含波动率水平。其三，综合考察不同风险溢价结构在样本内外的期权定价表现，发现单一风险溢价结构更加依赖模型参数的估计结果，而可变风险溢价结构则具有更加稳定的定价优越性。在考虑了不同样本长度、定价方法、定价区间以及期权产品后，以上结论依然稳健。

结合本文结论能够得到如下启示：第一，跳跃风险溢价在风险溢价结构中占据主导地位，表明了投资者对于跳跃风险的溢价补偿需求要远超过扩散风险，从而需要重点把控跳跃风险与尾部风险，防范“黑天鹅”事件对市场可能造成的冲击，做到事前及时监测预警、事中高效处理化解、事后强化监管治理。第二，由于跳跃风险溢价存在较强的时变特征，并且具有对隐含波动率曲面的解释能力，因此建议合理利用市场隐含信息做好投资者整体情绪与偏好的动态识别，加强部门沟通效率，实现对市场的精准把控。

未来的研究工作有：一是利用可变风险溢价结构提取市场中的隐含偏好信息，从时间维度分析重大事件冲击对于市场风险溢价结构的影响，从空间维度比较不同市场的风险结构特征，识别风险定价机制。二是考虑更为前沿的复杂随机模型，构建更为广义的可变风险溢价结构，进而更准确地刻画市场偏好，提升期权定价能力。 ■

[基金项目：国家自然科学基金项目“基于多元Hawkes跳跃互激发与波动率交叉回馈过程的期权定价研究”(项目编号：72071132)、国家自然科学基金项目“外部冲击、金融内生性与系统性金融风险研究”(项目编号：72173089)]

注释

1.参数变换关系

考虑如下的双变量Radon-Nikodym导数：

在此分别给出对数价格过程Xt在两个测度下的矩母指数表达式：

为得到参数变换关系，将 测度下的矩母指数整理为 测度的同样形式，即：

通过对比可得：

2.定价方法详细介绍

(1)解析解

此处给出Merton跳扩散模型下欧式看涨期权价格的表达式：

其中：

其可被视为在不同价格跳跃次数的条件下BS价格形式的加权平均，权重为发生对应跳跃次数的泊松概率。在实际应用时根据需求对(B1)式中的求和上限加以限制，忽略尾部带来的定价误差。根据市场上日度跳跃强度的参数估计水平与所定价期权的到期期限范围，将(B1)式中的求和上限设置为200。

(2)蒙特卡罗模拟法

该方法在时间维度下将资产在风险中性测度下的价格动态离散化，随机生成每个时间区间中的价格变化，模拟完整的价格变化路径。当模拟路径总数足够多时，依据大数定律可使用样本均值代替整体期望，从而计算出期权价格近似解。

具体而言，将时间区间[0,T]均匀划分为N份，其中每个子区间的长度记为τ(τ=T/N)，则相邻时刻间所对应的对数收益率ln(Sjτ/S(j-1)τ)为：

对于第m条价格路径，通过计算机模拟生成Xjτ-X(j-1)τ的取值，并累加出该路径下到期日的价格，按照上述方法共生成M条路径。本文中的参数取值为N=5000，M=10000。

(3)快速傅里叶变换法

该方法利用风险中性测度下标的资产对数价格过程的特征函数，借助傅里叶变换求解欧式期权价格的积分表达式，并使用离散求和近似，匹配快速傅里叶变换形式高效计算期权价格。

其借助标的资产对数价格过程的特征函数ϕT推导出看涨期权价格的积分表达式：

其中：

随后借助梯形法则配凑出FFT形式的离散求和近似解：

其中：

a代表有效求和上界。在本文中的参数设置为：N=4096，a=1024，α=2.5。

(4)格方法

该方法借助时间与价格维度双重离散的框架，通过对价格变动幅度进行分类实现扩散与跳跃行为的区分。不同于Amin(1993)所采用的递归算法，本文选择使用Fu et al.(2017)所提出的JDGF(jump-diffusion generating f u n c t i o n)算法，其具有封闭形式的欧式期权价格近似解。

其将时间区间[0,T]均匀划分成N份，子区间的长度记为τ(τ=T/N)，构造出0时刻到T时刻的价格路径α={S0,Sτ,…,Skτ,…,SNτ}。并假设不同时刻的价格变动相互独立，且相邻两个时刻的价格之比为指定常数u的整数次幂，即：

在风险中性测度 下，欧式看涨期权的价格Vcall则可表示为：

其中，PN(h)代表步长为N、高度为h的路径概率，计算方式如下：

而ρj为单步价格向上移动j个单位的概率，涉及到对连续跳跃分布进行离散化的关键部分。其基本思想是通过给定离散分布下价格变化的上下限，将每个离散价格变化节点左右一定范围内的概率作为该处价格变动的概率，并对部分细节做出调整使离散分布的方差与原连续分布尽可能相近。具体调整规则如下：

其中参数设置为：N=5000，R=40，跳跃上限I0=200。

(5)有限差分法

该方法通过对期权价格所满足的偏积分微分方程进行近似得到差分方程，并借助时间维度与价格维度双重离散的框架，从到期日开始进行反向递归求解期权近似价格。

对于Merton跳扩散模型而言，期权价格V(t,x)应满足如下的PIDE：

而有限差分法可视为求解PIDE的一种数值手段，对(B9)中的不同偏微分项采取如下差分近似方法：

化简后得到如下递推关系：

其将时间区间[0,T]均匀划分成N份，子区间的长度记为Δt(Δt=T/N)，将价格区间[A1,A2]均匀划分成M份，子区间的长度记为Δx。综合考虑定价精度与计算速度，本文中取N=1000，M=1000。

3.跳跃风险溢价关于定价核参数的单调性证明

综上所述，f(θ)在 上单调递增，证毕。

4.跳跃风险溢价关于定价核参数的单调性证明

对于到期期限为T的期权，构造收益序列{Rk}nk=1和无风险收益Rf，其中：

此时将收益序列{Rk}视为每个观测值具有相等概率pk的经验分布，作为真实概率测度。假设投资者具有HARA类的效用函数：

投资者通过调整合适的权重投资风险资产与无风险资产，最大化其期末的期望效用，可以计算出与风险厌恶系数γ对应的一组概率{qk}，即风险中性测度，其中qk计算方式如下：

γ>0时，

γ<0时，

γ=0时，

γ>0时，

γ<0时，

γ=0时，

得到风险中性概率{qk}后，看涨期权的价格计算公式如下：

同理，借助该设定下期权价格与等价鞅测度与定价核的一一对应关系，在已知市场期权价格以及真实测度下的经验分布后，可以反推其所对应的风险厌恶系数γ以及风险中性概率{qk}，从而计算出隐含的定价核。