基于TOF和自适应抗差卡尔曼滤波的UWB室内定位算法
方贤宝,林 勇,苏羿安,钟乐天
(合肥工业大学电气与自动化学院,安徽 合肥 230009)
0 引 言
随着移动通信、人工智能(AI)的蓬勃发展,定位技术早已走进人们的日常生活中,如室外定位技术中,全球定位系统(global positioning system,GPS)几乎覆盖人类的生产生活。与此同时,人们对室内定位的需求也与日俱增,工厂的智能生产、医院的高效救治、商场的货品搜寻等都需要准确的位置定位信息[1]。因此,将位置服务拓展到室内是一个急需解决的问题。超宽带脉冲(impulse radio of ultrawideband,IR-UWB)技术具有高带宽、高分辨率、高无线传输速率、超强鲁棒性、低能耗等显著优点,现已成为未来最具开发前景的室内无线定位解决方案之一[2]。常见的超宽带(UWB)定位技术分为4 类:基于飞行时间(time of flight,TOF)的[3]、基于到达时间差(time difference of arrival,TDOA)的[4],基于到达角(angle of arrival,AOA)的[5]和基于接收信号强度(received signal strength,RSS)的[6]。但在复杂的室内环境下,UWB 信号传播极易受到影响,从而造成定位精度降低。文献[7]使用Chan算法获取初始定位,比较残差与门限值鉴别与剔除非视距(non-line-of-sight,NLOS)误差,再利用改进无迹卡尔曼滤波(unscented Kalman fitering,UKF)算法得到精确的位置坐标;文献[8]提出对原始定位数据进行2 次粒子滤波,通过模型存储与权重调节,从而实现精准高效的动态目标定位;文献[9]利用抗差因子鉴别NLOS 误差,以削弱其对测距器造成的噪声干扰及影响,同时利用Sage-Husa 滤波算法进行估计和校正,最终使用卡尔曼滤波(Kalman filtering,KF)算法实现高精度UWB定位与解算。
造成UWB室内定位算法的误差为标准时间误差和多径效应,即在NLOS 环境下将大大降低定位误差。而上述文献只关注于消除NLOS误差,而忽略了标准时间误差,所以为了抑制标准误差和NLOS误差,提高定位算法的精度,本文提出一种基于TOF 和自适应抗差KF(adaptive robust KF,ARKF)的UWB 室内定位算法--IKF 算法。首先对UWB设备进行标定,实现对测距误差信息的快速修正;针对标准误差,使用改进的测距算法,优化定位;其次采用自适应抗差滤波算法抑制NLOS误差,提高定位精度。
1 UWB/TOF测距原理
1.1 UWB定位误差模型
UWB室内定位系统如图1(a)所示,主要由3个主从基站,1个标签以及路由器和服务器组成。室内定位系统中,基站与标签之间形成的信号直射传输路径往往容易受到室内装饰物或人员等障碍物阻挡,对此产生的信号误差一般可称为NLOS误差,信号的传播可以称为NLOS 传播,路径轨迹如图1(b)所示。
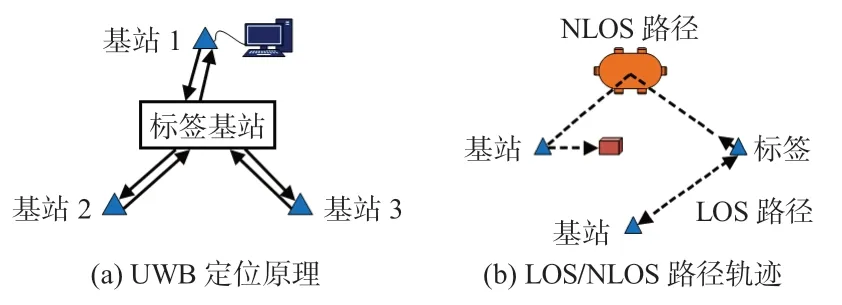
图1 UWB定位模型
假设在视距(line of sight,LOS)环境下,基站k与标签在ti时刻测量距离值为rk(ti),具体可表示为
式中Lk(ti)为基站k与标签在ti时刻的真实距离,nk(ti)为标准时间误差,由标准时间偏差带来的测量误差,包括脉冲信号在基站与标签之间的固定延时误差、器件误差,还与信号传播距离、室内温度等有关[10]。该类误差通常认为是均值误差为0,标准差较小的高斯随机噪声,可使用测距标定法消除部分,同时本文使用改进的测距算法进一步剔除,增加定位精度。在NLOS环境下,存在随机测量误差,误差模型表示为
式中 NLOSk(ti)为NLOS误差,服从指数、均匀、高斯或者δ分布,且与系统定位环境有关,可通过滤波算法降低其误差。
1.2 TOF测距原理
基于TOF 的测距原理为设备间互发信号,通过信号TOF与传播速度测量两者之间的距离。其方式主要有2种:单边双向测距(single-sided two-way ranging,SS-TWR)算法[11]与双边双向测距(double-sided two-way ranging,DS-TWR)算法[12]。
SS-TWR算法原理如图2(a)所示,先由设备A 向设备B发送测距请求,当设备B 接收该请求后,延迟一段时间Treply向设备A发送确认消息,经过Tprop设备A 接收。从设备A发送信息至接收,整个过程时间记为Tround。每个设备都对信号传输和接收的时间进行精确记录,最终计算出Tround和Treply,估算出最终的TOF,测量值与误差表达式如下
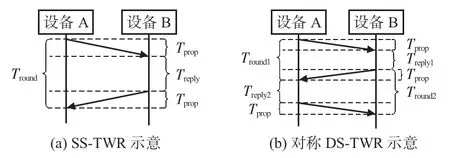
图2 TOF测距原理
其中,eA与eB为设备A和设备B 的时钟漂移,单位为10-6。该算法虽仅需一次信息交换即可得到测距信息从而降低功耗,但是TOF 估计误差随着Treply的增加而增加,令测距值存在较大误差,故SS-TWR 算法在实际情形下并不适用。
DS-TWR算法原理如图2(b)所示。设备A 发送UWB信号,经过Tprop后,设备B 接收并延迟一段时间Treply1后发送确认消息帧,设备A在接收后延后时间Treply2再次发送测距信息。最终TOF与估计误差如下
由式(5)可知,只有令设备的回复时间间隔一致,才可以降低由时钟漂移引起的标准误差。该算法虽降低了标准时间误差,但设备延迟时间必须尽可能相等,若不等,则将增大测距误差,进一步降低定位精度。
2 算法改进
2.1 基于对称DS-TWR方法的优化
由以上分析可知,SS-TWR算法仅需一次信息交换即可得TOF,但是误差大,DS-TWR 算法简单,仅需简单数学运算即可得到测距结果,但要求设备高精度,否则将引起较大误差。对此,本文提出一种基于DS-TWR 的改进算法,如图3所示。
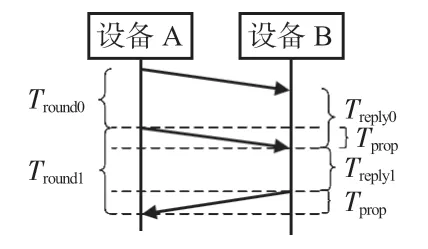
图3 DS-TWR优化算法示意
首先由设备A 发送测距请求信号,在等待时间Tround0后,再次发送测距请求,经过延迟时间Treply1与信号Tprop后,设备A接收到确认消息帧,其中,Tround0与Treply1为预先设定好的时间间隔。设备B第一次与第二次接收消息的时间间隔设为Treply0,且令其等于Tround0。Tround0和Tround1通过设备计时器得到,通过简单运算,有
真实值为
由以上公式可得该算法中测量值与真实值Tprop的误差为
由上式可知,该算法中测距误差仅与飞行实际时间Tprop和eB有关。由于SS-TWR算法误差较大,并不适用,仅对比DS-TWR算法与本文改进算法。例如,对于DS-TWR算法,假设当设备A与设备B应答消息延迟时间相差1 ms、时钟漂移之差为2 ×10-5,真实距离为300 m 时,计算出标准误差为5 ns,对此产生的测距误差为1.5 m;而本文测距算法中,信号传播时间的实际值为1 000 ns,当设备B 的时钟漂移eB最大为20 ×10-6,TOF误差仅为0.04 ns,测距误差为1.2 cm。相比DS-TWR 算法,该算法降低了标准时间误差,提升了测距精度。
2.2 基于KF算法的优化
KF是一种线性滤波器,可以根据上一时刻的系统状态和预测状态,对系统下一时刻的真实状态进行推测的最优估计算法[13]。KF 本身是一种递归过程,由以下5 个递归方程组成
式中Ak-1与Bk-1分别为状态转移矩阵和输入控制矩阵,Qk-1为过程噪声协方差矩阵,Uk-1为系统控制量,Hk为观测模型矩阵,Rk为过程噪声协方差矩阵。Kk为卡尔曼增益,对最优估计^Xk进行比例调节,其大小反映了在最优化状态值估计过程中“更相信”观测值Zk还是估计值。
KF算法能够对数据进行线性滤波,结合观测值与测量值,最终得到系统的最佳估计值。但在复杂的室内环境下,室内装饰与人员等都会遮挡UWB 信号,形成多径效应,带来NLOS误差,使得定位估计值出现偏差。因此,本文提出抗NLOS KF算法,通过比较残差与3 倍信息的方差来判断LOS与NLOS情形,若存在NLOS则对增益进行缩放以减小测距误差。
测量的部分异常值是在k时刻的最优估计时首次被引入,若能预先将计算所得的残差进行修正,再继续进行滤波最优估计,则可以有效消除部分异常值,将残差矩阵Δk和方差矩阵Dk定义为
依据3倍方差理论和上式,得到如下判断公式
式中为Dk矩阵对角线上的第i个元素,为Δk的第i个元素,当上式不满足时,则受到NLOS误差,进行修正
式中α为修正系数,决定了对NLOS误差的抑制效果。在实际情形中,UWB使用场景受到的NLOS误差不是唯一的,因此对α取固定值不符合实际。所以,为进一步提高抗NLOS误差的效果,需要依据残差与方差的对应关系来调节α的值
其中,b为调制指数,控制着修正指数的放大与缩小。当处于移动情形下,定位精度会受到NLOS 误差而发生变化,相对应的残差也会改变,所以需要调节修正系数α在1 -b至1不断变化,达到自适应抗NLOS 误差的效果。在本文中,最终经过实验验证,修正系数α设为0.8,最大缩小比例b设置为0.4可达到最佳实验效果。
3 实验与验证结果
实验布置如图4所示。图4中,标签位于Pi处,基站分布四周,分别使用KF算法和本文算法进行滤波,最后使用三边定位法进行定位,使用式(16)计算定位误差,比较定位精度
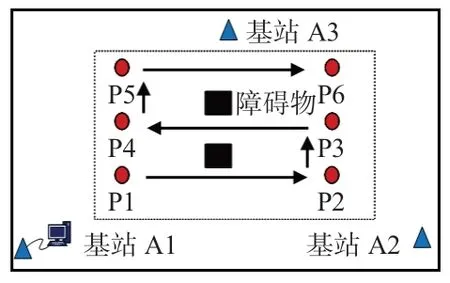
图4 实验环境示意
其中,(x,y)为定位算法解算得到的标签坐标,(xt,yt)为标签实际坐标。
3.1 UWB测距标定
为进一步消除定位误差,本文实验依次对实验设备进行测距标定[14]。实验在逸夫楼4 楼一个空实验室内进行,大小为6.5 m×8 m,实验环境中基站与标签之间无遮挡物,无实验人员穿行,为相对意义下的LOS环境。首先对基站A1 进行测距实验标定:基站A1 不动,标签由近及远选择10个待测点,通过测距仪器测得的距离作为真实值,标签与基站A1测得的数据在使用3σ原则剔除较大误差数据后取平均值作为量测值,对2种测量数据进行一次线性拟合,确定误差模型,完成基站的标定,其余基站同理。表1 为UWB各基站的校正参数。其中,拟合优度的数值越接近1,表明拟合程度越好。

表1 基站校正参数
3.2 UWB静态定位实验
表2列出了LOS环境下,2 种算法在静态时定位误差的数据对比。可以看出,在观测环境较好的情形下,2 种算法的精度相当,但IKF 算法精度仍有较小的提高。因为本文使用了改进的TOF算法和测距标定,剔除了标准误差,一定程度上提高了定位精度。

表2 静态测试点LOS环境定位误差比较
表3为在NLOS环境下的静态定位实验结果。可以看到:KF算法的最小误差达到约30 cm,而IKF算法最大误差仅为20 cm左右,平均定位误差大幅度降低。整体上,本文提出的算法可以在NLOS环境下有效且准确地对系统进行静态定位。
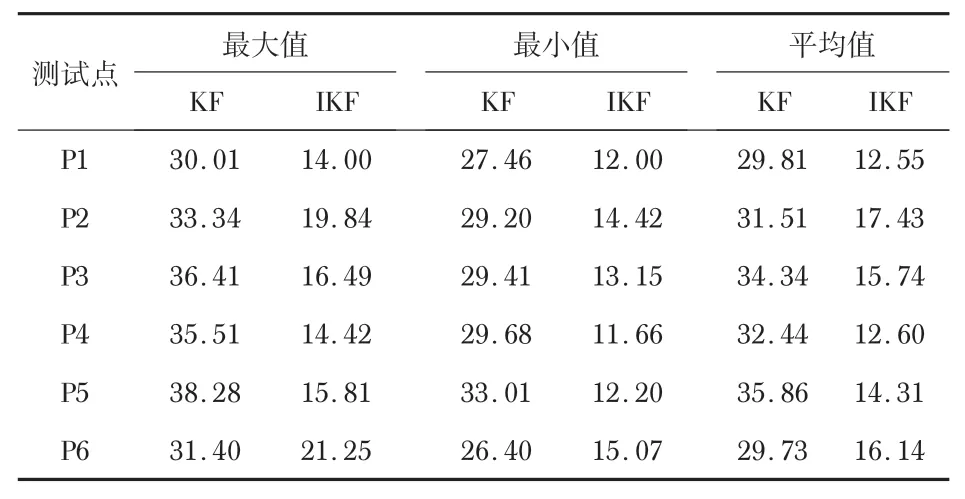
表3 静态测试点NLOS环境定位误差比较
3.3 UWB动态定位实验
在本文实验中,实验人员携带标签从P1 出发,依次经过P2,P3,P4,P5,直至点P6,整体呈现5 字型,进行LOS与NLOS环境下的动态定位实验,人员以正常匀速移动。如图5 所示,ARKF 算法与KF 算法在2 种环境下的定位轨迹。

图5 2 种算法在LOS环境下的动态定位比较
从图5中的2幅图对比看出,在LOS环境下,2 种算法的动态定位结果相差不大,但KF算法仍有较少部分的断点与轨迹偏移,而本文算法基本贴合原路径。在NLOS 环境下,如图6 所示,KF 与ARKF 算法皆有一定的误差,但KF算法却有部分断点,偏离原路径,最大误差达到50 cm,而本文算法动态定位较连续,无较大偏差,可以达到20 cm以内,最大误差仅25 cm,定位效果较好,定位精度较高。
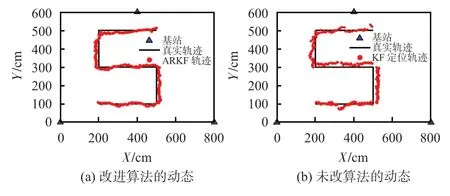
图6 2 种算法在NLOS环境下的动态定位比较
4 结束语
在UWB测距过程中,易受包括器件误差、延时误差在内的标准误差以及NLOS 测距误差等因素的影响,导致测距精度大幅度降低。针对前者,本文提出一种改进的TOF算法,并对设备进行测距标定,利用一次线性拟合剔除测距过程中的标准误差;通过比较残差与3 倍信息的方差判断是否有NLOS存在,以此减小NLOS 误差。实验结果表明:本文提出的改进算法能够有效剔除标准时间误差与NLOS误差,提高定位系统在复杂室内环境下的定位精度。

