基于模拟退火和樽海鞘群优化的DV-Hop定位算法*

张大龙，孙 顶，张立志，郭仕勇，韩刚涛

（郑州大学网络空间安全学院，河南 郑州 450002）

0 引 言

无线传感器网络（WSNs）是由大量的传感器节点以自组织和多跳的方式构成，具有数据采集、处理和传输的功能。其中，节点定位技术［1］是WSNs 中最基础也是最重要的技术之一。节点定位技术包括基于测距的定位技术和基于非测距的定位技术。后者对传感器的硬件复杂度和算力要求不高，被大多数传感器网络所采用。DV-Hop算法是基于非测距定位算法中应用最广泛的一种，如何提高该算法的定位精度成为了近年来WSNs 领域中的热门研究方向。文献［2］利用节点间的接收信号强度指示（received signal strength indication，RSSI）值量化节点间的跳数，从而减小跳数误差；文献［3］则采用扫描全局信标节点的信息的方法对跳距进行修正，减小跳距带来的误差。考虑到DV-Hop算法未知节点估计过程可视为在全局范围内寻找最优解的过程，因此许多研究者选择将群智能优化算法与WSNs 相结合，如文献［4］采用改进的鲸鱼优化算法代替最小二乘法计算未知节点的坐标；文献［5］提出将Levy飞行策略与灰狼优化算法相结合，从而进一步提高未知节点估计精度；文献［6］将灰狼优化算法的狼群狩猎思想和绵羊优化算法的羊群互动思想相结合，改进狮子群优化算法并应用于未知节点坐标定位的优化。

本文针对传统DV-Hop 算法在计算跳数、跳距以及未知节点估计过程中存在的误差，采用RSSI 值进行跳数量化，引入修正因子对平均跳距进行校正，在未知节点估计阶段提出基于模拟退火和樽海鞘群［7］优化的DV-Hop定位算法：通过改进的Tent 混沌映射［8］优化樽海鞘群初始位置，引入惯性权重策略改进樽海鞘群的更新机制，再利用模拟退火算法［9］的概率突跳特性缓解群优化算法容易陷入局部最优的问题。仿真结果表明，本文提出的改进算法能够有效提高未知节点定位精度。

1 传统DV-Hop算法原理

传统DV-Hop算法可分为3 个阶段：确定最小跳数、计算平均跳距以及未知节点估计。

第一阶段：信标节点将包含自身唯一标识、位置信息和初始跳数为0的数据表以泛洪的方式广播给通信范围内的其他节点，每个节点仅保存与周围其他节点间的最小跳数值。

第二阶段：多次泛洪后，信标节点获取到与周围其他信标节点之间的最小跳数和位置信息，根据式（1）计算出各自的平均跳距Hopsizei

式中 （xi，yi），（xj，yj）为信标节点i和其他信标节点j的位置坐标；hij为信标节点i和j之间的最小跳数。则未知节点与信标节点间的估计距离du，i可表示为

式中hu，i为未知节点u与信标节点i的最小跳数。

第三阶段：利用第二阶段中计算出的未知节点与各个信标节点间的估计距离，采用最小二乘法进行三边定位。假设未知节点坐标U＝（x，y），根据式（2）得到各个信标节点与未知节点的距离方程组如式（3）所示

利用最小二乘法得到的解为

其中

式（4）中的U即为未知节点的坐标估计位置。

2 改进的DV-Hop算法

2.1 基于RSSI的跳数量化

不少研究者对于传统DV-Hop算法最小跳数的优化提出了多种方法，文献［10］中采用二通信半径策略计算最小跳数值；文献［11］中引入Ochiai系数来逼近相邻节点间的通信重叠面积，来改进现有的连续跳数模型。鉴于目前大部分传感器节点集成了RSSI 测量设备，因此，本文根据RSSI的对数-常态分布模型所计算出的接受信号强度，对信标节点通信范围内的未知节点跳数进行量化，RSSI的对数-常态分布模型如式（7）所示

式中d0为参考信号传输距离，m；P（d0）为接收信号强度，dB；一般情况下，d0＝1 m；n为射频信道的衰减指数，一般取2～4；dij为节点间的欧氏距离；Xσ为均值为0、方差为σ的高斯随机分布，σ的取值根据节点间的通信环境而定。

选取信标节点通信半径R作为理想单跳距离且将该位置的信号强度值作为单跳距离的基准信号强度RSSIR，则第i＋1个节点接收到的第i个节点的信号强度值为RSSIi，i＋1，根据此值，第i＋1个节点的量化规则如式（8）所示

2.2 平均跳距校正

针对传统DV-Hop 算法中计算平均跳距存在的误差，文献［3］根据全局信标节点特性与未知节点局部信标节点对定位精度的影响，提出HDCD算法；文献［12］通过筛选参与平均跳距计算的信标节点并对其进行加权处理，从而减小引入的误差。本文则通过引入修正因子［4］来对信标节点的平均跳距进行校正。假设2个信标节点在泛洪过程中接收到了对方的位置信息，则两信标节点的实际距离d与估计距离＾di，j，如式（9）、式（10）所示

根据两两信标节点之间平均每一跳的实际距离d与估计距离＾di，j的误差，定义修正因子ei如式（11）所示

因此，校正后的平均跳距如式（12）所示

2.3 基于模拟退火和樽海鞘群优化的未知节点估计

DV-Hop算法中未知节点估计问题可以看作在全局范围内搜索未知节点坐标的最优解问题。文献［4］中利用改进的鲸鱼优化算法代替最小二乘法，从而提高定位精度。文献［13］引入数学优化模型来限定人工蜂群算法的寻优范围，从而减少了定位阶段的误差和计算量。

同样，受樽海鞘群聚行为的启发，2017 年，Mirjalili S等人提出了一种全新的群智能优化算法--樽海鞘群算法，该算法可以用来解决未知节点估计过程中定位误差较大，全局信息利用率低的问题，但同时也存在寻优过程中容易陷入局部最优的缺点［7］。针对这一问题，本文提出基于模拟退火的樽海鞘群优化算法，利用模拟退火算法的概率突跳特性［14］在解空间中随机搜索最优解，即在樽海鞘群算法陷入局部最优解时能够概率性地跳出并且最终得到全局最优。

2.3.1 构建适应度函数

本文根据参与定位的信标节点与未知节点间平均每一跳的距离与估计距离之差作为构建适应度函数fitness（x，y）的准则，如式（13）所示

其中，（x，y）为未知节点坐标，（xi，yi）为参与定位的信标节点坐标，＾dui为未知节点与信标节点间的估计距离，N为参与定位的信标节点个数，hui为未知节点与信标节点间的最小跳数。适应度函数fitness（x，y）的值越小则说明未知节点（x，y）的坐标越接近真实的未知节点坐标，适应度越高。

2.3.2 改进的Tent混沌映射种群初始化

由于在群优化算法中，种群的初始化位置将会影响整个算法的收敛速度，初始化的种群在空间内分布越均匀，越有利于算法的寻优效率和定位精度。Tent映射产生的混沌序列分布均匀，但会产生小周期以及不稳定周期点。因此，本文采用一种改进的Tent 映射［8］产生的混沌序列作为种群的初始化位置，映射关系如式（14）所示

其中，rt为区间（0，1）上的随机数，NT为Tent混沌序列中的元素数量。

根据式（14）产生混沌序列x后，樽海鞘群在搜索空间［lbj，ubj］内的初始化位置如式（15）所示

2.3.3 樽海鞘群的位置更新

假设种群个数为N的樽海鞘群利用改进的Tent 混沌映射初始化种群位置，计算每个个体的适应度fitness（xi，yi），并将所有个体按照适应度由高到低排序，选取其中适应度函数值最小（适应度最高）的个体mini∈［1，N］｛fitness（xi，yi）｝，即全局最优位置，作为食物源Fj。然后将适应度前50%数量的樽海鞘规定为领导者，进行全局探索；其余部分为追随者，充分进行局部探索。领导者位置根据式（16）进行更新

式中ubj，lbj为搜索空间的上限与下限；c2，c3分别控制下次移动的长度和下次移动的方向，取值皆为［0，1］之间的随机数；c1的作用是平衡开发与勘探，定义如式（17）所示

式中l为当前迭代次数，Lmax为最大迭代次数。

追随者的位置则根据牛顿运动定律进行更新，如式（18）所示

重复上述步骤，每次迭代都会重新选出适应度最高的位置作为食物源，直到达到迭代次数上限，此时的食物源即为樽海鞘群优化算法的全局的最优解。

2.3.4 惯性权重策略

上述式（16）和式（18）为原始樽海鞘群算法中领导者与追随者的位置更新策略。对于种群中的追随者来说，其位置更新策略受领导者的位置影响；对于第i只追随者来说，其位置更新受第i-1 只追随者的影响。为了平衡樽海鞘群优化算法的全局搜索能力和局部搜索能力，本文引入基于非线性递减函数的惯性权重因子来衡量樽海鞘个体之间的影响，改进后的追随者更新策略如式（19）所示

式中wini为初始惯性权重，wend为最终惯性权重。随着迭代次数l的增加，惯性权重因子w（t）随之减小，即第i只追随者的位置受第i-1 只追随者的影响随着迭代次数的增加会逐渐减小，局部探索能力增强，从而使得樽海鞘群优化算法的全局搜索能力和局部搜索能力得到平衡。

2.3.5 模拟退火流程

首先对模拟退火算法进行初始化，初始温度T为充分大。假设退火过程中能量从S1变化到S2，则能量变化量ΔC＝S2-S1。其中，S2表示樽海鞘更新状态后的适应度值，S1表示樽海鞘更新状态前的适应度值。根据Metropolis 算法［15］准则，如式（20）所示，p表示当前状态接受更新后的樽海鞘位置的概率

对于ΔC＜0的樽海鞘，更新后的适应度高于更新前的适应度，即表示更新后的位置要优于更新前的位置，则这种更新将会被接受；对于ΔC≥0 的樽海鞘，更新后的适应度不如更新前的适应度，即表示更新后的位置相比于原位置更加偏离实际位置，这种情况下，改进算法不会立刻舍弃该更新位置，而是会在（0，1）区间内生成一个均匀分布的随机数ε，如果ε＜p，则此时的位置更新被接受，否则拒绝更新，樽海鞘保持更新前的位置

最后根据式（21）进行退火操作，其中，λ为温度下降速率，一般取值为0.8～0.99。重复上述位置更新策略以及模拟退火流程，当最终温度达到终止温度水平，即算法到达设定的最大迭代次数；或者适应度函数值到达所设定的适应度门限要求时，停止迭代，将此时的食物源Fj，即全局最优位置输出作为未知节点的最终估计坐标。

2.4 改进的DV-Hop算法流程

1）根据RSSI值量化后的跳数与修正因子校正后的平均跳距计算出未知节点与周围信标节点的估计距离，并且利用式（13）构建适应度函数。

2）在搜索空间内通过改进的Tent 混沌映射得到分布均匀的初始化樽海鞘群，并初始化模拟退火算法。

3）计算种群中所有个体的适应度函数值，确定食物源并划分种群领导者与追随者。

4）分别利用式（16）和式（19）计算更新后领导者与追随者位置。

5）计算更新后的种群个体适应度，通过模拟退火流程中的式（20）判断是否接受更新后的樽海鞘个体位置。

6）根据式（21）进行退火操作。

7）重复上述步骤（3）～步骤（6），直到达到最大迭代次数或者满足适应度门限要求，输出此时食物源作为未知节点估计坐标。

3 算法仿真与结果分析

采用仿真软件MATLAB 2017a 作为仿真平台进行实验，将本文改进算法与传统DV-Hop、文献［16］中提出的算法，记为SADV-Hop算法和文献［17］的IGWODV-Hop 算法进行对比仿真。如图1 所示，仿真环境为100 m ×100 m 的矩形区域中随机布设一定比例的信标节点与未知节点，网络连通性如图2所示，节点的分布和网络连通性符合实际环境中的分布情况。对比算法中的适应度函数均采用式（13）的形式，采用归一化的相对定位误差作为衡量算法定位精确度的标准

图1 网络连通性示意

图2 节点连通性示意

其中，（xi，yi），（xreal，yreal）分别为未知节点估计坐标与未知节点真实坐标。N为未知节点数量，R为通信半径。

3.1 信标节点比例对定位精度的影响

设置通信半径为30 m，节点总数为100 个，信标节点比例由10%逐渐增加到40%，进行100 次随机实验，将得到的结果求均值。信标节点比例与归一化的相对定位误差之间的关系如图3（a）所示：随着信标节点的比例增加，4 种算法的定位误差都随之减小，原因是当信标节点比例较小时，未知节点周围的信标节点信息匮乏，定位精度较低，随着信标节点比例的增加，定位精度逐渐增高，但是当信标节点比例过大时，对定位精度的影响会逐渐变小。本文算法相比于传统DV-Hop算法、SADV-Hop算法与IGWODV-Hop算法定位精度分别提升了36.7%，16.2%，9.1%。

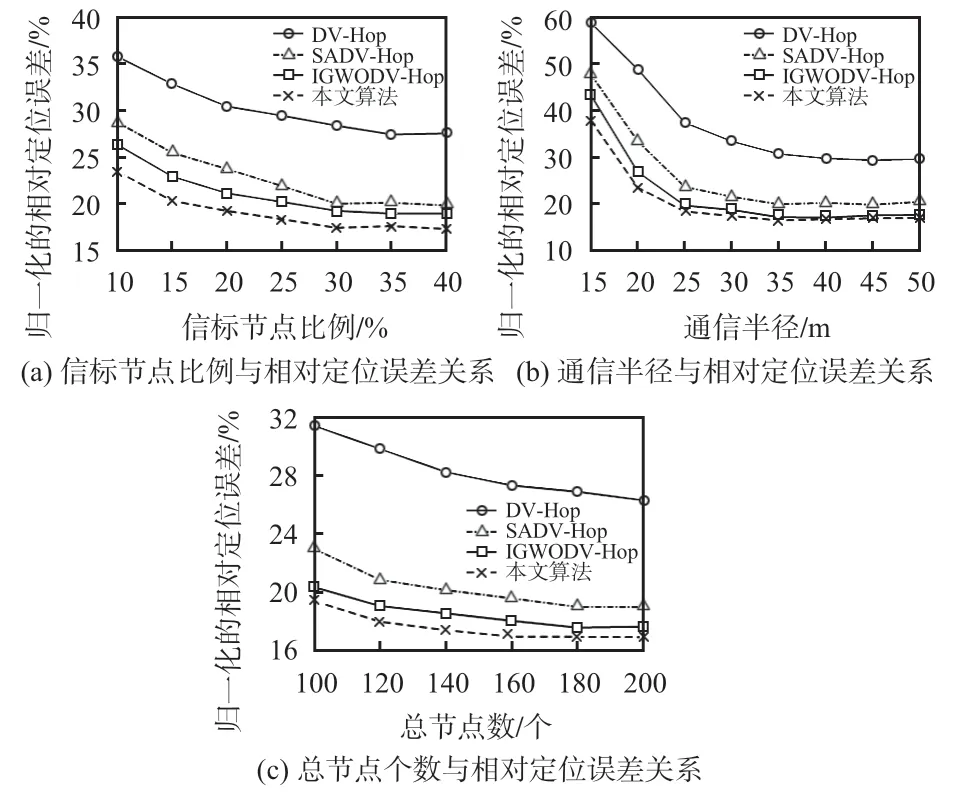
图3 性能测试结果

3.2 通信半径对定位精度的影响

设置节点总数为100个，信标节点比例为30%，通信半径由15 m逐渐增加到50 m，进行100次实验，将得到的结果求均值。则通信半径与定位精度的关系如图3（b）所示：当通信半径在15～30 m变化的过程中，4种算法的定位精度快速提升，之后再扩大通信半径则归一化相对定位误差曲线变化平缓甚至有所回升，原因是：通信半径的增加使得网络连通性增强，未知节点能够利用的位置信息增多，但是在过大的通信半径下，未知节点接收到的冗余信息也增多，不利于未知节点的定位。本文算法相比于传统DV-Hop 算法、SADV-Hop算法与IGWODV-Hop算法定位误差分别降低了43.6%，19.3%，7.5%。

3.3 总节点数量对定位精度的影响

设置通信半径为30 m，信标节点比例为30%，总节点数由100个逐渐增加至200 个，进行100 次随机实验，并将得到的定位结果求均值。则总节点个数与归一化的相对定位误差之间的关系如图3（c）所示：在100 m×100 m的仿真环境下，增加总节点个数，则信标节点的密度和整个网络的连通度都会提升。同样，当总节点个数过多时，网络中的冗余信息也会增加，因此当总节点个数大到一定程度时，总节点个数对定位精度的影响会非常微小。本文算法相比于传统DV-Hop算法、SADV-Hop算法与IGWODV-Hop算法定位精度分别提升了38.0%，13.2%，5.1%。

4 结束语

针对传统DV-Hop算法定位精度较低等问题，本文对定位算法3 个阶段提出改进算法：基于RSSI 值的跳数量化机制、基于修正因子的平均跳距校正以及基于模拟退火的改进樽海鞘群优化算法。在经典樽海鞘群优化算法中采用改进的Tent 混沌映射对种群的初始位置进行优化，并且在樽海鞘位置更新过程中引入惯性权重策略平衡樽海鞘群优化算法的局部搜索能力和全局搜索能力，最后将其更新策略与模拟退火算法相结合，缓解樽海鞘群优化算法易陷入局部最优的缺点，该算法相比于其他的智能群优化算法在定位精度上有着明显提高，但是算法的复杂程度也略有提升，下一步的研究重点在于降低算法的复杂度。