基于热电耦合模型和AUKF的锂电池内温状态估算*

张峰凡，张良力，刘 江

（1.武汉科技大学信息科学与工程学院，湖北 武汉 430081；2.武汉科技大学冶金自动化与检测技术教育部工程研究中心，湖北 武汉 430081）

0 引 言

锂（lithium，Li）电池内芯温度变化伴随电池充放电全过程，与环境积温共同影响锂电池可用性能剩余比例（state of health，SOH）［1］。在内温变化下构建近似线性系统状态方程，通过观测电压、电流输出值对锂电池荷电状态（state of charge，SOC）进行最优估计，结果难保准确。文献［2］外采锂电池壳表温度对SOC进行补偿估值，在提高准度的同时丧失了实时性；文献［3］基于经典传热学理论，建立锂电池内温状态（state of internal temperature，SOIT）在储能装置的电池管理系统（battery management system，BMS）中，与热失控风险等级直接关联。在锂电池正常工作状态下，SOIT亦可作为约束条件协同估准SOC。

热电耦合模型在物理等效单元呈耦合态，但各自近似线性系统状态方程互不影响。各自利用模型参数辨识方法，仍能完成状态方程构建。文献［4］提出一种简化的热电耦合模型，采用扩展卡尔曼滤波（extended Kalman filtering，EKF）算法实现电池内温在线估计；在此基础上，文献［5］提出基于简化可变参数热模型（simplified variable parameter thermal model，SVPTM）的热电耦合模型并同样使用EKF估算SOIT，但EKF 在雅可比矩阵推导和线性化精度等方面存在不足。

锂电池内部极化电阻时变热效［6］，对模型参数辨识增加难度的同时，与系统噪声相叠加，对后续锂电池SOIT 估算造成严重影响。本文提出一种基于双重极化热电耦合模型的锂电池内温自适应无迹卡尔曼滤波（adaptive unscented Kalman filtering，AUKF）估算方法。改进的双重极化电路模型用于描述锂电池内部生热因素与SOC、环境积温三者之间的关联；为降低SOIT估算过程受热效等噪声影响，引入自适应机制更新相关噪声协方差矩阵，提升无迹卡尔曼滤波（unscented Kalman filtering，UKF）估算SOIT的准度。

1 锂电池等效热电耦合模型

1.1 锂电池等效热电耦合模型

锂电池生热是锂离子在正负极上发生嵌入、脱嵌、转移时的正常现象［7］，除欧姆热之外，其主要组分为极化热，表现为锂电池内部电解液发生浓度差极化反应、电化学极化反应时的热物理特性。考虑了上述2种极化反应产生的热变化，对传统锂电池等效电路模型的影响，含有双重极化效应的锂电池等效电路结构如图1所示。

图1 改进的双重极化电路模型

其中，Ut为端电压，Uocv为开路电压（open circuit voltage，OCV）；R0为欧姆内阻，Rp1C1为锂电池内发生浓度差极化时的等效电阻电容，Rp2C2为电化学极化时的等效电阻电容。R0，Rp1，Rp2均为以锂电池SOC 值、环境积温T为自变量的函数。

1.2 等效热建模

锂电池中熵热相比于阻抗热可忽略不计［8］，内芯热值Q＝I2R0＋I2（Rp1＋Rp2）。其中，I2R0为焦耳损耗热，I2（Rp1＋Rp2）为双重极化损耗热。若锂电池芯体纵向均匀，则假定电池径向生热远小于纵向生热［9］，锂电池等效热模型如图2 所示。图中，Cc，Cs分别为锂电池内芯、壳体热容；Ri，Ru分别为内芯、壳体热阻。位于结点处的Tc，Ts，Ta分别为锂电池内芯温度、表面温度、环境温度。设Tcs＝Tc-Ta，Tss＝Ts-Ta，锂电池热量传递过程表达式为

图2 锂电池等效热模型

1.3 双重极化热电耦合建模

由上述分析可知，忽略锂电池内芯热值Q的等效电路模型，其充放电电流I可作为观测值，用于模型参数辨识并估算SOC。而考虑双重极化的热电耦合模型中部分电流会产生焦耳损耗热和双重极化损耗热，使锂电池内温升高并对SOC估算形成噪声影响。以SOIT估算为目标的锂电池内部热电耦合过程如图3所示。

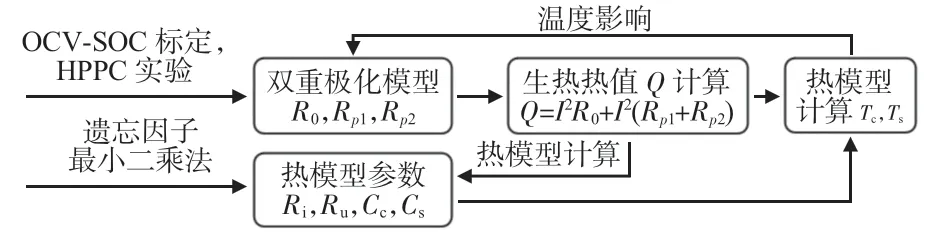
图3 双重极化热电耦合流程

2 热电耦合模型参数辨识

2.1 等效电路参数辨识

选取锂电池（标称容量为2000 mAh，标称电压为3.7 V）实施恒流放电（OCV-SOC 标定）实验和混合脉冲功率特性（hybrid pulse power characteristics，HPPC）实验［10］。为保障环境温度恒定并获取实时数据，引入恒温箱和无纸化温度记录仪。设置截止电压上、下限分别为4.2 V和2.75 V，考虑环境积温对电路模型参数的影响，分别将锂电池置于单一恒温环境（0，25，45 ℃）进行OCV-SOC 标定实验和HPPC实验，根据实验平台在锂电池SOC 值0.1～0.9 时刻记录的观测数据进行模型参数辨识，拟合双重极化参数分别与SOC、环境积温三者之间的空间映射关系如图4所示。

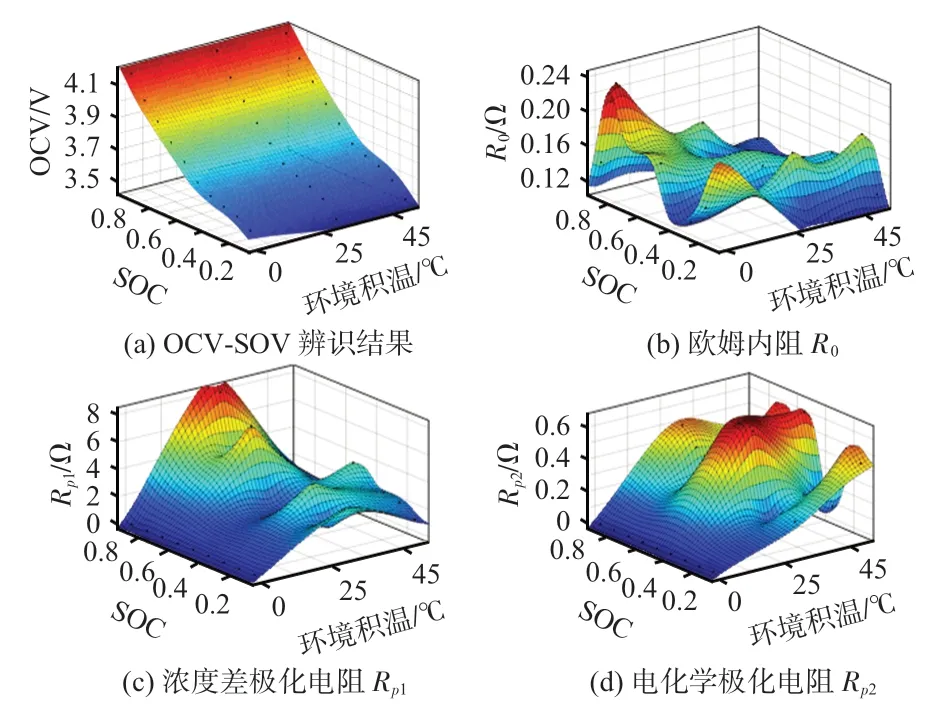
图4 拟合参数空间映射关系

2.2 热模型参数辨识

带遗忘因子的递推最小二乘法可强化新数据的特性，逐渐削弱旧数据的作用，在一定程度上解决了数据饱和问题［11］。锂电池等效热模型拉普拉斯（Laplace）方程为

式中G（s）为系统传递函数，s为Laplace算子。对图2 所示等效热模型，以式（2）内参数作为对象实施在线辨识。设y（k）＝Tss，输入向量为Q（k），对式（4）进行拉氏z变换可得系统差分方程为

式中a1，…，a5为待估计参数，取遗忘因子为0.98，锂电池热模型参数计算式为

式中 锂电池为铝制外壳，则Cs由锂电池的铝热容、外壳厚度、尺寸等自身特性参数计算得到，将式（2）代入式（4），得到热模型参数辨识结果：Cs＝4.6 J／K，Cc＝63.5 J／K，Ri＝1.93 K／W，Ru＝2.938 K／W。

3 基于AUKF的锂电池SOIT估算

UKF通过某种计算规则构造出Sigma 点集，间接逼近非线性系统的状态分布，使自身能有效避免由系统非线性加剧引起的滤波发散问题［12］。结合锂电池热电耦合模型，定义系统状态变量x＝［TcsTss］T，观测变量z＝Ts，输入变量u＝［Q Ta］T，观测噪声为v，系统过程噪声为w，Q，R分别为观测噪声和系统过程噪声的协方差，系统离散状态空间方程可表示为

其中

锂电池因内温升高形成的热噪声规律未知，极易造成UKF失败。此时需将UKF 与自适应协方差匹配法进行结合，形成AUKF，通过测量值同其预测值之间的新息序列，完成对过程噪声协方差、测量噪声协方差的估计修正。无迹变换后更新过程如下：

1）状态预测及状态协方差预测更新

2）测量预测及测量协方差预测更新

3）联合协方差及卡尔曼增益更新

4）状态变量和状态协方差更新

5）自适应噪声协方差匹配更新

式中ek为新息矩阵，Hk为自适应噪声协方差矩阵，L为协方差匹配开窗矩阵。

4 实验分析

为获得锂电池内温与表面温度，将贴片型负温度系数温度传感器置于锂电池内部极柱和外壳处，使用恒温箱实现各种环境温度恒定。

4.1 恒流放电实验

设置环境温度为5 ℃，以1C 恒流实施锂电池放电实验。UKF与AUKF方法得出的锂电池SOIT估算结果以及误差对比情况如图5 所示。在恒温条件下，UKF 与AUKF均接近于实际SOIT值，但AUKF在误差绝对值及估算过程进入稳态耗时，优于UKF方法。

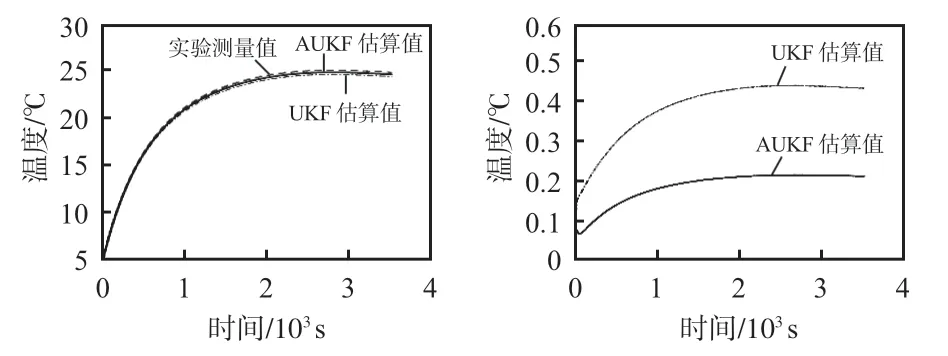
图5 1C恒流放电下SOIT估算及误差对比

4.2 动态压力测试实验

使用过程中的锂电池在遇到安装底座振动、空气湿度盐度变化时，内部电流、电压可能随之发生波动情况，与锂电池在理想状态下内部自发热叠加，共同影响UKF／AUKF估算结果的准度。在环境温度20 ℃下，以动态压力测试（dynamic pressure test，DST）电流、电压作为锂电池的激励输入进行实验，其DST电流、电压随时间变化如图6所示。

图6 DST电流、电压曲线

在DST实验下SOIT估算及误差对比如图7 所示。可看出，UKF和AUKF在估算过程仍与实际SOIT值变化保持同步，但UKF估算结果准确度已明显低于AUKF。估算初期，UKF和AUKF估算误差均处较低水平；随着实验推进，二者估算误差开始累积增大，UKF 估算SOIT 最大误差为0.81 ℃，AUKF估算最大误差为0.46 ℃。当噪声模型发生更大幅度变化时，UKF 估算结果无法紧随实际值变化，而AUKF通过噪声协方差的实时更新，对噪声模型的变化有较强的自适应能力，估值结果更加贴近实际值。

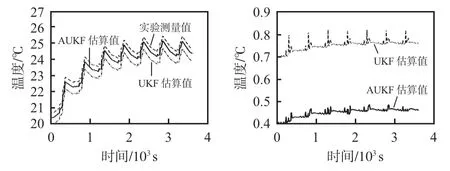
图7 DST实验下SOIT估算及误差对比

5 结 论

忽略锂电池内芯热值影响，将全部充放电电流用作观测值进行模型参数辨识并进行SOC估算，必然导致估算结果不准。而考虑双重极化的热电耦合模型是将锂电池充放电电流分出一部分，转换为焦耳损耗热和双重极化损耗热，形成温升效应并与等效电路呈耦合态，虽在一定程度上增加了模型参数辨识复杂度，但更能体现出锂电池内部真实状态，有利于锂电池状态值估算方法改进，提升估算准度。

在指定恒温下实施恒流放电、DST，比对UKF和AUKF在2次实验中估算SOIT性能发现，UKF和AUKF在估算过程中均能与实际内温值变化保持同步。当外界因素引发锂电池内部电流电压波动加剧时，AUKF 通过内部噪声协方差自适应实时更新机制，比UKF 更能抑制住SOIT 估算值误差趋大的走势。这对提升锂电池SOIT估算准度，以及为接续估算SOC、SOH等锂电池状态值提供准确的热规律有实际意义。