球槽模型压力极大值位置是否存在质量比临界值

闫俊卿 姚华鑫 林云强

(1.安徽省安庆市田家炳中学,安徽 安庆 246003; 2.北京师范大学未来教育学院,广东 珠海 519087; 3.安徽省安庆市石化第一中学,安徽 安庆 246002)

1 引言

球槽模型是高中物理教学中一个比较经典的模型,涉及动量与能量的综合分析,经常会涉及特殊位置处相互作用力的分析.关于球槽模型大部分文献旨在探讨球槽模型小球对地速度最大值位置是否存在质量比临界值,如文献[2]～[5]都得出球槽质量比影响小球速度最大值出现的位置.而小球对凹槽压力极大值的出现位置的研究文献较少,翻阅文献发现对此问题有不同的观点:文献[1]指出考虑小球的质量和转动惯量会影响小球对凹槽最大压力的出现位置,且凹槽质量等于小球质量是压力极大值偏离最低点的临界条件;而文献[4]指出小球对凹槽的压力的最大值与质量比无关,在凹槽最低点出现.那么压力的最大值究竟是否存在质量比临界呢?基于以上研究背景,本文将从一般化情形和理想化情形进行分析,定量推导小球所受支持力的表达式,并进行数值模拟来分析两者的规律,从而揭示真实的物理过程和规律.

为方便下文论述,把考虑小球半径和转动惯量的情况称为一般化情形,把小球视为质点模型的情况称为理想化情形.下文将探讨小球对凹槽压力的规律及极大值的出现位置与质量比是否有关.

2 定量分析 探寻规律

情境描述:质量为M,半径为R的凹槽静止在光滑的水平地面上,一个质量为m,半径为r的小球,从凹槽圆心等高处静止释放.

2.1 一般化情形研究

2.1.1 理论推导

小球沿圆轨道滚动的过程中,某时刻情境如图1所示,令小球相对于凹槽圆心O的速度vC方向垂直于球心与凹槽圆心O的连线,设此时连线与竖直方向的夹角为θ,此时凹槽水平向左的速度为v,凹槽对小球的支持力为N以及小球所受的重力为G.

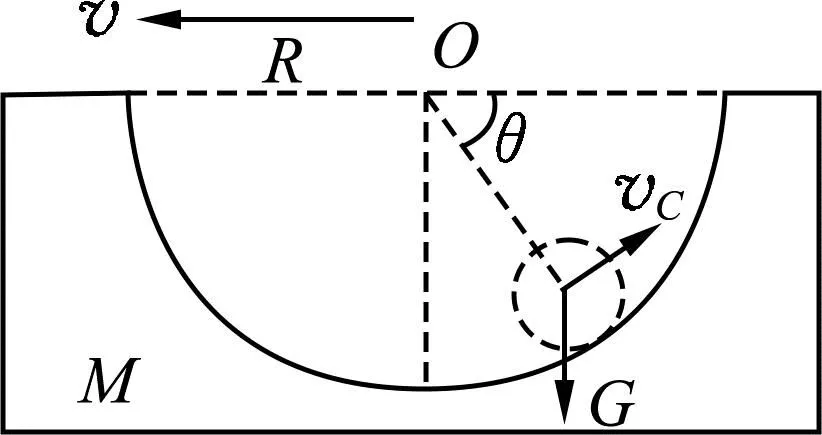
图1 情境图

根据伽利略变换可知小球相对于地面水平向右的速度大小为vCsinθ+v,根据水平方向动量守恒可得

m(vCsinθ+v)+Mv=0.

(1)

以小球在轨迹最低点处的球心所在平面为零势能面,从与圆心等高处运动到此时的状态,根据机械能守恒定律可得

(2)

根据柯尼希定理可知小球相对于地面的总动能T等于质心相对于地面的平动动能和小球相对质心的转动动能之和,故有

(3)

又因为小球相对于凹槽做无滑滚动,可得

vC=rω.

(4)

小球沿凹槽向上运动的过程中,凹槽具有向右的加速度,于是以凹槽为非惯性参考系,小球受到向左的惯性力F′,其大小为F′=Ncosθ.

以凹槽为参考系,小球球心相对于圆心做圆周运动,径向由牛顿第二定律可得

(5)

联立式(1)～(5)解得

(6)

从N的数学表达式看出,该表达式不含r和R,说明球槽半径的大小和小球的转动惯量不影响压力极值的出现位置.那么压力又会呈现出什么规律呢,接下来通过数值模拟,更加直观地进行呈现和分析.

2.1.2 一般化情形规律可视化

为方便研究,我们取m=1 kg,R=1.0 m,r=0.1 m,g=10 m/s2.同时令M/m=M=k.由牛顿第三定律可知,压力大小满足FN=N,二者方向相反.故式(6)可化为

用数学软件GeoGebra绘制的FN图像如图2所示.

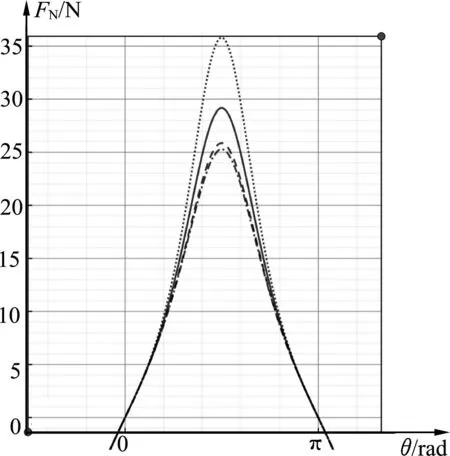
图2 一般化情形FN的函数图像

限于篇幅,这里仅仅给出4种情况下的FN的函数图像.当我们不断增大k值时,FN的函数图像的差别在于极大值发生变化,即有函数极大值随着k的增大而减小,而函数图像的整体对称性依然相同.从FN与θ的函数图像可以看出,FN的函数图像的对称轴始终为θ=π/2,而且函数最大值始终出现在θ=π/2处.前文一般化情形中将小球和凹槽圆心的连线与水平方向的夹角设为θ,即有小球对凹槽压力极大值在凹槽最低点处取得.

2.1.3 一般化情形规律总结

因此,归纳得到以下结论:在考虑小球大小和转动惯量的情况下,无论凹槽与小球的质量之比取何值,小球对凹槽压力的极大值始终在凹槽的最低点处取得.

从物理角度阐释该结论:不同的球槽,无论小球半径如何,球槽的质量比如何,小球的压力的极大值都出现在凹槽的最低点,并且压力的变化规律相同.这无疑是该情境背后隐藏的另一个有趣的、简洁的、对称的、美丽统一的物理规律.

这不免引发进一步思考,既然小球半径和凹槽质量比不影响压力变化规律和其极大值出现的位置,那么就可以将小球视为质点,该模型简化为下文中的理想化模型进行再次探究.

2.2 理想化模型研究

2.2.1 理论推导

理想化情形下,我们忽略小球自身的半径(即不考虑其转动惯量),将其视为质点,探究小球对凹槽圆轨道的压力的规律及极大值出现的位置.此时系统运动情境如图3所示,v1代表小球的速度,v2代表凹槽的速度,v相代表小球相对于凹槽的速度,小球和圆心的连线与水平方向成θ角,显然v相沿圆轨道的切线方向.

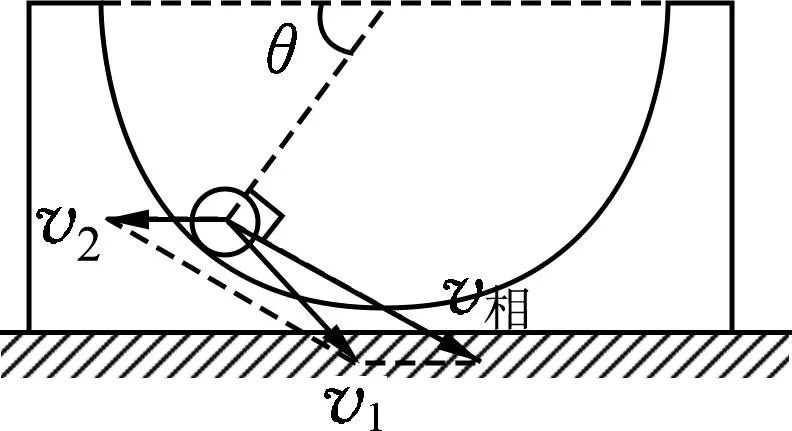
图3 情境图

小球从水平位置滑到图示位置的过程,由机械能守恒可得

(7)

其中v12=(v相sinθ-v2)2+(v相cosθ)2.

(8)

由水平方向动量守恒可得

mv1x=Mv2.

(9)

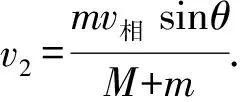
(10)

联立式(7)～(11)可得

(11)

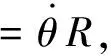
(12)

(13)

解得关于θ的微分方程为

(14)

于是对θ求二阶导数可得

(16)

将式(16)代入式(15)化简可得

(17)

(18)

对式(18)求导可得

(19)

代入式(15)和式(16)即有

(20)

以圆槽为参考系(非惯性系),小球受到圆槽给其的沿半径方向的支持力,设此时凹槽水平方向的加速度为a2,小球在球槽参考系中受到水平方向的惯性力F′,且大小为F′=ma2,与圆槽此时的水平加速度方向相反.小球对圆槽由牛顿第二定律可得

(21)

联立式(13)(15)(20)(21),可得

(22)

从上式中FN的表达式可知,小球对凹槽圆轨道的压力与凹槽半径R无关,与小球和凹槽的质量以及角度θ有关.于是,我们将尝试改变小球和凹槽的质量关系,数值模拟更加直观探究小球对凹槽压力的规律.

2.2.2 理想化情形规律可视化

为方便观察N的变化规律,同理我们取m=1 kg,R=1 m,g=10 m/s2.同时令M/m=M=k,则式(22)可化为

我们用数学绘图工具GeoGebra绘制的FN图像如图4所示.

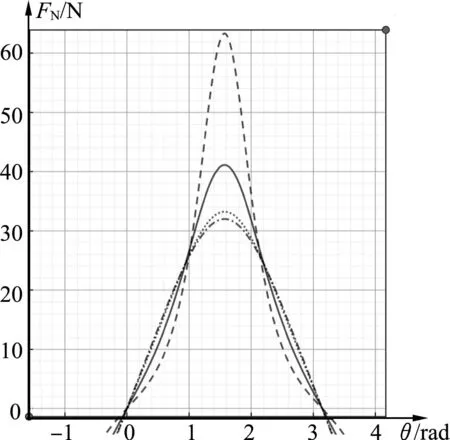
图4 理想化情形FN的函数图像

从图4中可知FN函数图像始终存在一个极大值,且始终存在一个对称轴.绘图软件自带的数据显示,FN函数的极大值在θ=1.5707963…处取得,这说明函数极值在2θ=π处取得,即无论小球与凹槽的质量之比取何值小球的速度最大值始终在最低点处取得.

2.2.3 理想化情形规律总结

从数学表达式,规律的数值模拟可视化,可以得出无论小球与凹槽的质量之比取何值,小球的速度最大值始终在最低点处取得.

这说明两种情形下小球对凹槽圆轨道压力的极大值始终在轨道最低点处取得且改变小球与凹槽的质量比值不影响压力极大值的出现位置.

2.3 两种情形分析和比较

第一,相同位置,压力大小不同.

从图3和图4,我们发现两种情形下小球运动到同一位置所受支持力大小不同,小球视为质点情形压力明显大于非质点情形.其实物理原因很简单,就是考虑小球转动惯量会把一部分动能用于自身的转动,从而小球相对凹槽的速度大小变小,于是对凹槽的压力也因之变小.当然,考虑小球半径也会使运动相同θ位置时减少的重力势能变小,于是获得的总动能也相应变小,即有小球的速度产生微妙的变小,从而有压力变小.

第二,同种情形,k不相同,压力变化规律略有差异,变化趋势相同.

当小球质量远大于凹槽质量即k值比较小时,分析原因也很简单,小球开始阶段近似于做自由落体运动,速度增加得比较快,因而相互作用时其对凹槽的压力短时间内增加加快,因此k值较小时,图像呈现出“细腰”的图像,k值较大时,不明显.

第三,两种情形,k相同压力变化规律相同.

由一般情形的理论推导得到的表达式,不含有球槽的几何参量,大胆猜测,球槽的半径不影响压力的变化规律,进而简化为理想模型处理,得出类似的规律,进而两种情形压力的极大值位置也不存在质量比临界问题,这无疑在讨论压力规律时,可以将小球视为质点,为球槽模型简化,提供了参考依据.

3 总结与启示

综上所述,得出研究结论:无论是否考虑小球的半径和转动惯量,还是改变小球与凹槽的质量之比,小球对凹槽的压力变化规律相同,且极大值出现位置始终在凹槽半圆轨道的最低点,与小球最大速度出现在最低点存在质量之比临界值截然不同.

诚然,上述分析与定量推导是基于文献[1]的矛盾展开的,文献[1]之所以出现错误结论,是因为在计算小球在半圆轨道任意位置受到的向心力时代入的小球速度是相对于圆轨道的速度大小,而不是绝对速度.所以,本文也为广大一线教师认识球槽模型的最大速度出现位置与最大压力出现位置的差异提供了参考.

教师在物理试题的命制过程中,把握好正确的物理结论显得尤为重要.当高中物理的知识不能解决面临的物理问题时,教师可采用大学物理学的方法进行推导并得到正确的结论.这也启示教师在日常教学中关注物理结论成立的条件并勇于发现问题解决问题,防止思维定式的产生.